基于等值面体的三维涡旋数量与形状特征研究1)

陈 槐 张 磊 王乃茹 朱立俊

* (南京水利科学研究院水文水资源与水利工程科学国家重点实验室,南京 210029)

† (中国水利水电科学研究院水利部泥沙科学与北方河流治理重点实验室,北京 100038)

引言

湍流兼具随机性和相干性,其基本组成结构是各种尺度的涡旋,背景流场中存在大量随机性的小尺度涡旋,还存在时间或空间上相关性很强的大尺度涡旋,涡旋被誉为流体运动的肌腱[1].由于涡旋与湍流、大气现象、海洋物理、流体控制、升增减阻和气动噪声等方面关系密切,涡旋研究在航空航天、水利、海洋、动力机械和仿生学等领域工程应用中具有重要的意义[2].

涡旋被掩盖在杂乱的湍动场中,需要利用特定的方法进行提取,最常用的是参数阈值法,其建立在局部速度梯度张量的基础上,具有伽利略不变性,与参考系无关,主要分以下4 类[3]: (1)第二不变量Q＞0,表征了局部空间内的旋转率大于应变率;(2)压力Hessian 矩阵的第二特征值λ2＜ 0,表征了特定平面内的旋转率大于应变率;(3)判别式Δ＞ 0,表征速度梯度矩阵存在复特征值;(4)旋转强度λci＞ 0,为梯度矩阵复特征值的虚部,表征了涡旋旋转的角速度.

虽然涡旋已经研究了几十年,但鉴于三维涡旋结构的复杂性,已有文献一般采用前述参数(Q,λ2,Δ及λci)某一固定阈值条件下的三维等值面体进行可视化,定性描绘三维涡旋结构的空间形态及其演化特征[4-17].当要定量描述三维涡旋时,为简化难度,已有文献主要是从平面二维流场中开展分析,量化涡旋的形态属性,如数量、尺度及方向等(相关文献较多,不再罗列,可参见文献[3]引言).然而,这些涡旋二维形态的研究结果(仅列举代表性文献[18-24])很大比例是建立在Wu 等[24]的研究思路基础上,选用不同壁面距离下的旋转强度均方根对旋转强度进行归一化,使各展向平面内旋转强度的概率密度函数曲线基本重合,由此得到涡旋识别的统一阈值.虽然这个方法看似阈值统一,实则阈值沿壁面距离发生改变,由其所得的结果必定与直观认识的涡旋结构(可视化时采用固定阈值)存在较大的差异,还会在某种程度上“扭曲”读者对三维涡旋结构的理解.

为了还原涡旋结构的真实三维形态属性,本文直接从涡旋可视化时利用的三维等值面体出发,研究三维涡旋的形态属性,达到所见即所得的效果,而不必像先前那样采用两套不同流程(可视化时采用三维流场下固定阈值,定量计算时采用二维流场下变阈值).

本工作采用两三角形相交快速检测算法,提取涡旋多边形,利用数量与形态参数(圆度、半径、凸状及纵横比因子)刻画三维涡旋的形态属性,并研究涡旋等值面体的阈值与壁面距离对涡旋形态的影响规律.研究结果以期有助于进一步深入理解涡旋的形成、发展和衰亡以及涡旋之间、涡旋与其他因素(如泥沙颗粒)之间的相互作用规律和机理.

1 数据及方法

1.1 DNS 数据

本文采用Del-Alamo 等应用DNS 方法获得的槽道湍流数据,该数据几乎模拟出槽道湍流中所有的含能结构,被广泛应用于相干结构的研究[5,22,25].槽道流的摩阻雷诺数为Reτ=uτh/ν=934,其中uτ为摩阻流速,h是槽道垂向半高,ν是动力黏滞系数,x,y及z分别对应流向(沿水流方向)、垂向(垂直于床面向上) 及展向(槽道展宽方向),详细数值见表1,其中Δx和Δz是x和z方向的网格分辨率,Δyc是槽道中心的网格分辨率,Nx,Ny及Nz是对应的网格数;上标“+”表示用内尺度(uτ和ν)进行无量纲化,如Δx+=Δxuτ/ν.

表1 DNS 槽道湍流计算参数Table 1 Parameters of the DNS channel flow dataset

1.2 涡旋识别方法

在众多的涡旋识别方法中,旋转强度法应用广泛,它能区分背景剪切,具有明确的物理意义(涡旋旋转的角速度),可提取涡旋的旋转平面及旋转角速度,并在涡结构可视化时对阈值的要求较低[3].令Mij=∂ui/∂xj(i,j=1,2,3,其中1,2,3 分别表示沿流向x,垂向y,展向z方向)是三维不可压流场中任意一点(x,y,z)的三维速度梯度张量,其特征方程为

其中Q=0.5tr(−MM),R=−det(M).利用卡丹公式求解此一元三次方程,当判别式Δ=(R/2)2+(Q/3)3＞0 时,方程存在一个实数根及一对共轭复数根,旋转强度即是复数根的虚部,其表达式为

1.3 涡旋形态因子提取方法

利用移动立方体算法快速生成涡旋的三维结构等值面体,并设置三角形切面对其进行剖分,通过两三角形相交快速检测算法,提取涡旋三维结构等值面体的切线,构造封闭多边形,由此计算三维涡旋的形态因子(如圆度、半径、凸状及纵横比因子),量化涡旋三维结构形态,具体步骤如下.

(1)在某一旋转强度阈值下(一般采用某一高程平面或某一立方体内的归一化旋转强度或旋转强度最大值衡量),利用移动立方体算法[26]快速生成涡旋的三维结构等值面体(以三角网格为单位,见图1 中绿色等值面体).

图1 涡旋等值面体与三角形切面Fig.1 3D vortex structure indicated by isosurface of swirling strength and a triangular cutting plane

(2)在某一高程y+处,设置xz面内的三角形切面对涡旋三维结构等值面进行切割(见图1 中红色切面),通过两三角形相交快速检测算法[27],提取大的三角形(切面)与每一小三角(等值面体的最小构成单元)间的相交线,由此得到非常多的切线段.

(3)利用涡旋的物理属性(一个首尾相连的闭合多边形),将步骤2 中的切线进行筛选,仅保留那些首尾各有一条其他切线相连的切线,并组合成封闭多边形,从而提取出该三角形切面内的所有涡旋的位置信息(见图2(a)),为避免误差影响,仅保留那些多边形的最小外接边界框长、宽都大于网格最小尺寸(3.8+)的涡旋.

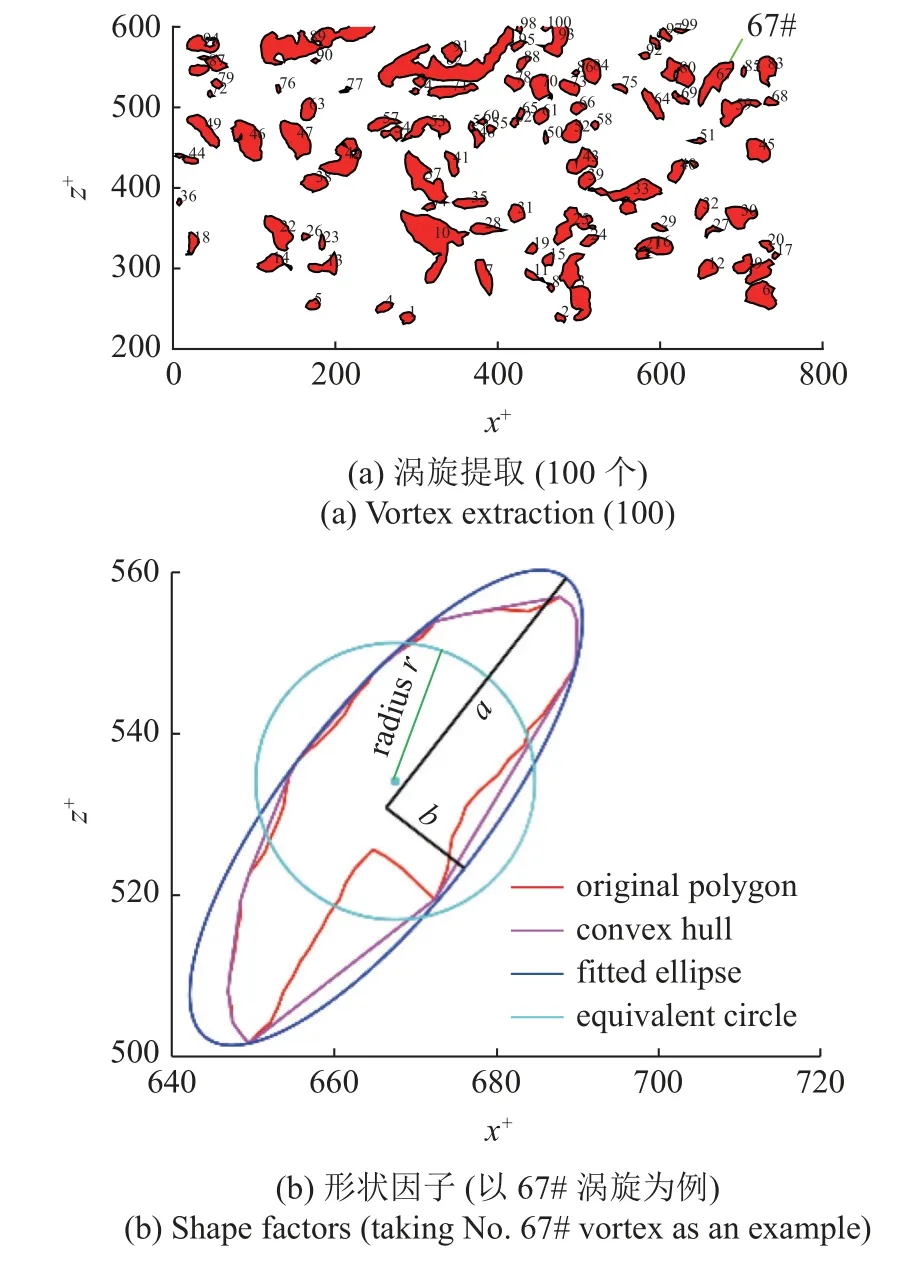
图2 涡旋提取与形状因子定义Fig.2 Vortex extraction and shape factors definition

(4)令步骤3 中提取的任意一个涡旋的节点坐标按逆时针方向排序为(xi,zi) (i=1,2,···,N),其中i为某个节点的序号,N为节点总数,则涡旋的形状因子公式(见图2(b))如下[28]

其中,O为圆度因子,面积湿周,r为半径因子,c为凸状因子,Ac是涡旋多边形的凸包(Graham 算法)所围成的面积,E为纵横比因子,a与b分别是涡旋多边形最小外接椭圆(Khachiyan 算法)的长轴与短轴.凸状因子反映出封闭曲线的弯曲程度,如果曲线完全外凸(曲率大于0)则凸状因子等于1,如果曲线有内凹(曲率小于0)则凸状因子小于1.以67#涡旋为例,其圆度、半径、凸状及纵横比因子分别为0.45,17.16,0.82 及0.32.

2 计算结果

2.1 结果验证

图3 给出了对数区y+=110 平面内本文结果与前人结果的对比.Gao 等[5]采用参数阈值法提取涡旋结构,计算步骤简要概括为: 计算平面内所有网格点的旋转强度值,标记出数值超过0.13 倍最大值的点,并筛选出局部极大值点作为涡旋核心,利用区域生长算法提取涡旋边界,最终计算涡旋半径.值得指出的是,当利用区域生长算法计算时,涡旋尺寸最少需要满足9 个点(即一个涡旋中心点与8 个外围点),所以Gao 等[5]提取出的涡旋最小半径为,体现为概率密度函数(PDF)曲线在r+=9 时出现极大值.为与前人对比,本文也计算了T=阈值下的涡旋等值面体,并利用切面法提取涡旋半径,由于会保留满足涡旋多边形最小外接边界框长、宽都大于3.8 的涡旋,所以本文的涡旋半径最小可以接近1.07).

图3 本文结果与前人结果涡旋半径PDF 对比图(y+=110,样本数量9 423 250)Fig.3 Comparison on PDF of vortex radius between this study and previous study (y+=110,the number of samples is 9 423 250)

由图可知,由于采用区域生长算法,Gao 等[5]的计算结果无法捕捉到r+＜ 9 的涡旋,造成其涡旋半径PDF 曲线没有峰值,只在r+=9 处出现极大值;反观本文,由于采用切线法,可以精确地捕捉出小尺度的涡旋,得到更符合物理意义的涡旋半径PDF 曲线,涡旋半径在r+=6.5 处出现峰值.此外,由于区域生长算法的限制及网格尺寸略大的原因,造成Gao 等[5]提取的涡旋半径要略大于本文计算结果,但两者的PDF 曲线在r+＞ 9 区间内变化规律基本一致.

2.2 阈值对形状因子的影响

由于涡旋的三维结构等值面体是在某阈值下生成的,所以阈值的大小会显著影响等值面体的大小.对于涡旋结构而言,旋转强度阈值越大,等值面体所构成的涡管就会越细,相应的涡旋半径就会越小.由于量化涡旋三维结构过于复杂,已有文献中一般仅通过研究某一平面内的旋转强度场来研究涡旋的属性(如数量、尺度及方向等),阈值取为该平面内旋转强度最大值的0.08～0.32 倍[5-6,12,16].为研究涡旋三维结构等值面体的阈值对涡旋形状因子计算结果的影响,本文以对数区内y+=110 平面为例,研究阈值范围条件下涡旋的数量与形状因子的变化规律.

图4 给出了阈值对涡旋提取数量的影响.将涡旋数量转为无量纲化涡旋密度,即其中N是涡旋数量,x与z方向模拟区域尺寸分别为=3πuτ/ν.可知,阈值越大,涡旋提取密度越小.当阈值从0.05 增加至0.5,涡旋提取密度从10−2降至10−6,虽然阈值仅增加了一个量级,但涡旋密度却降低了4 个量级.涡旋提取密度与阈值关系基本为对数关系,拟合曲线表达式为lgΠ=−8.25T−1.67,拟合相关系数R2=0.995 8.

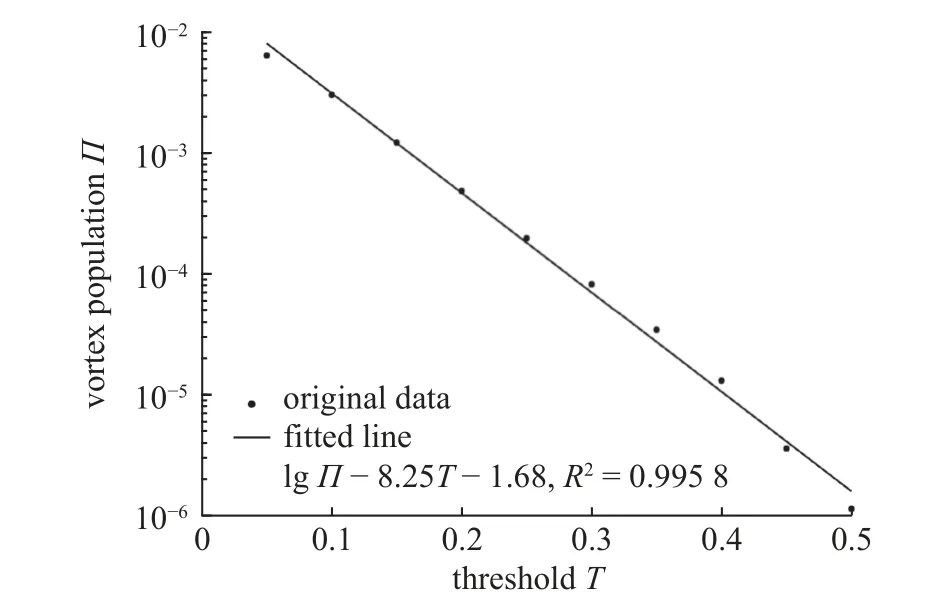
图4 阈值对涡旋提取密度的影响(y+=110)Fig.4 Influence of threshold on the number of extracted vortices(y+=110)

图5 给出了阈值对涡旋形状因子概率函数的影响,值得指出的是,圆度、半径及纵横比因子采用概率密度函数PDF 表示,而凸状因子由于其PDF 曲线在各阈值下过于紧凑,只能采用概率累积分布函数CDF 将其区分.

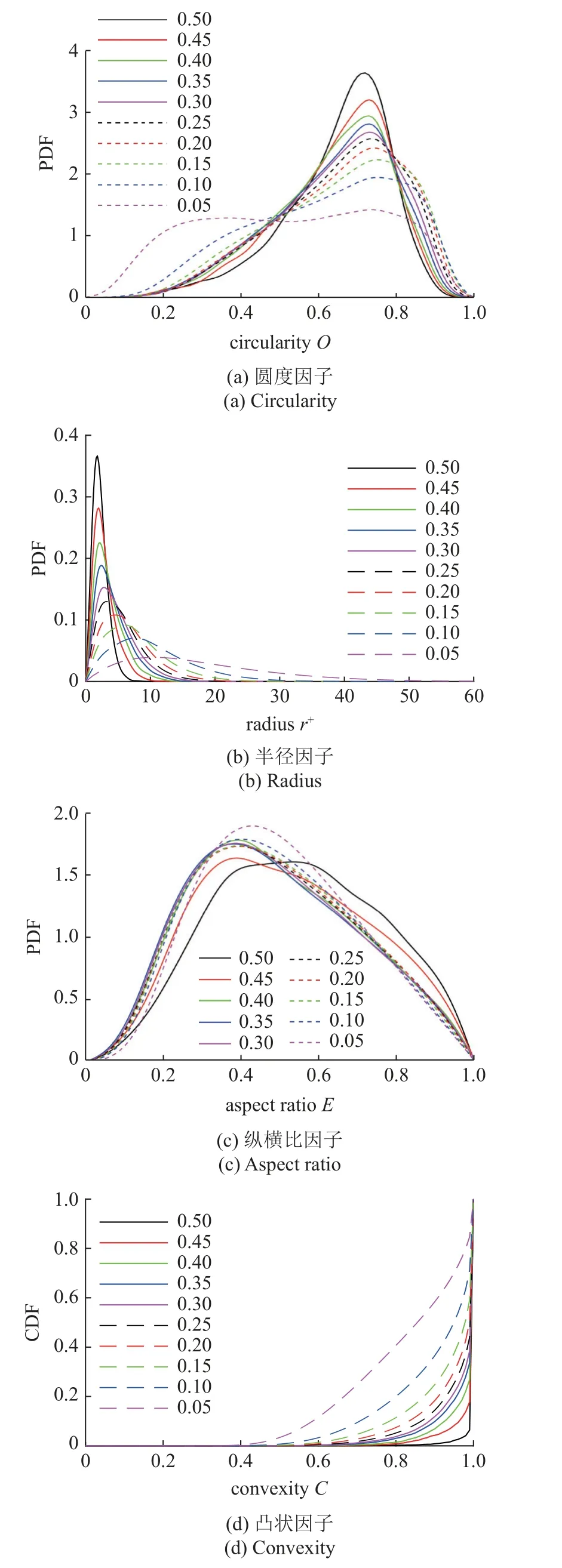
图5 阈值对涡旋形状因子概率函数PDF 及CDF 的影响(y+=110)Fig.5 Influence of threshold on PDFs and CDFs of vortex shape factors (y+=110)

对于圆度因子,当阈值很小时,其PDF 曲线比较平坦,类似均匀分布,表明此时的涡旋主要以非圆形态存在;随着阈值逐渐增大,PDF 曲线慢慢变得高耸(左偏分布),各阈值间的PDF 曲线也逐渐重合,表明涡旋形态逐渐稳定,并主要以类圆形态存在(众数为0.73).

对于半径因子,当阈值较小时,等值面体接近涡旋边缘,所以得到的涡旋半径较大;当阈值较大时,等值面体接近涡旋核心,所以得到的半径较小.PDF 曲线簇变化规律与圆度因子相似,随着阈值增大,PDF 曲线逐渐高耸并重合(众数在2 左右);两者不同的是,半径因子PDF 曲线是右偏分布.

对于纵横比因子,其PDF 曲线随阈值的增加并未显著变化,仅右偏程度稍有减小,PDF 曲线簇基本重合在一起(众数分布在[0.4,0.5]区间).可知,在各阈值下,涡旋多边形的最小外接椭圆形状统计规律基本一致,长、短轴长度比值在2～2.5 范围内的椭圆最多.

对于凸状因子,可以通过观察CDF 曲线的斜率来反映其PDF.当阈值很小时,涡旋的凸状因子数值主要分布在[0.4,1]区间内,且在[0.6,0.9]区间内PDF 基本呈均匀分布(CDF 曲线斜率相同),说明此时大部分涡旋多边形都不饱满,它们的轮廓存在凹陷,且凹陷程度都较大.随着阈值的增加,涡旋凸状因子数值分布区间逐渐变窄并向1 靠近,当阈值达到最大值时,其CDF 和PDF 曲线都类似脉冲函数,说明随着阈值的增加,涡旋多边形逐渐变得饱满,轮廓几乎不存在凹陷了.

图6 给出了阈值对涡旋形状因子均值的影响.随着阈值的增加,圆度因子的均值先增加随后基本在0.65 附近波动,表明涡旋形状先不断变得更圆,随后基本稳定不变;纵横比因子的均值始终在0.5 上下波动,并未出现较大程度改变,表明涡旋外接椭圆长、短轴比值约维持为2;凸状因子均值始终在增加并最终接近1,表明涡旋多边形趋于饱满;半径因子均值递减,当T＜ 0.2 时递减速度较大,此后递减速度基本维持不变.

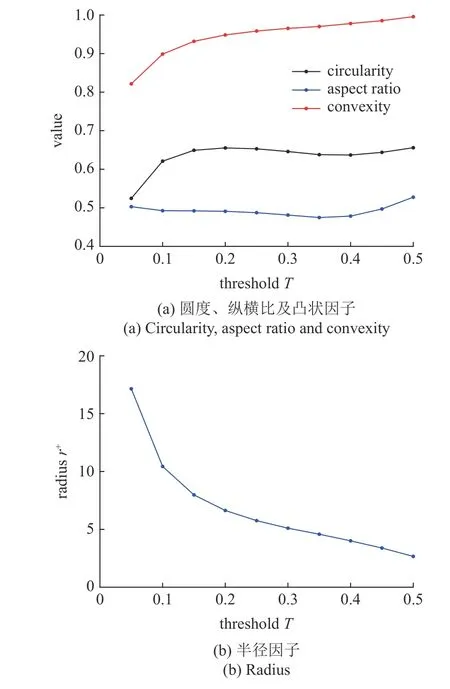
图6 阈值对涡旋形状因子均值的影响(y+=110)Fig.6 Influence of threshold on mean values of vortex shape factors(y+=110)

2.3 壁面距离对形状因子的影响

前人在可视化涡旋三维结构时采用参数阈值法(Q,λ2,Δ或λci),利用某一固定阈值下的等值面体定性描绘涡旋三维结构,而已有关于涡旋二维切面的形态属性(数量、尺寸及方向)的定量研究结果都是建立在沿壁面距离变阈值的思路基础上,这种变阈值提取的结果在某种程度上“扭曲”了我们对真实三维涡旋结构的理解,亟待研究固定阈值下的相关结果.

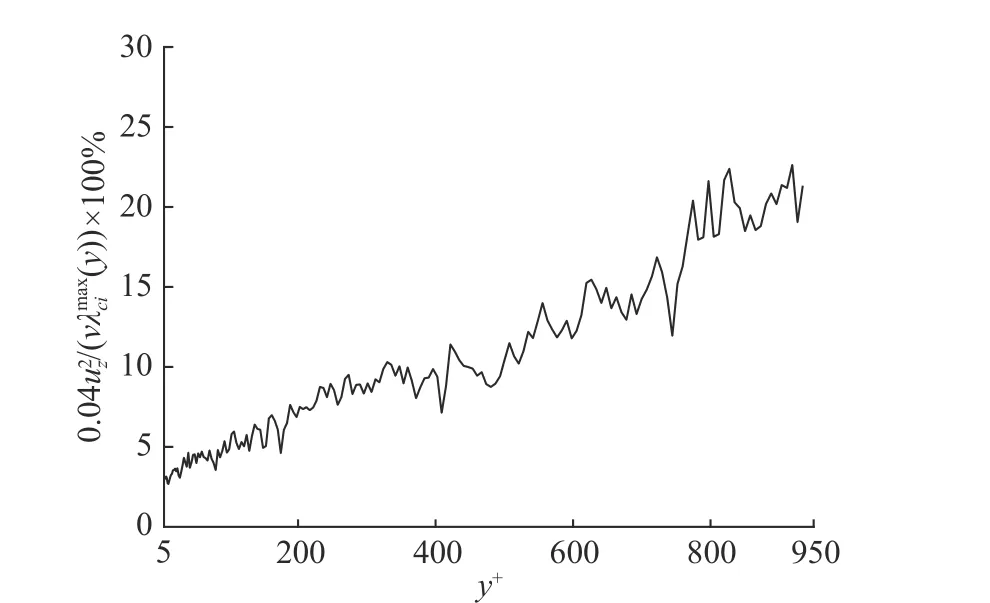
图7 固定阈值()与各zx 平面内旋转强度最大值()(y)的比值Fig.7 Ratio of fixed threshold (=0.04) to the maximum swirling strength in each zx-plane ()(y)

图8 给出了壁面距离对涡旋提取数量的影响.随着壁面距离的增加,涡旋密度在缓冲层内逐渐增加,并在对数区内达到最大值,此后沿程不断衰减,极大值与极小值在全域相差约一个量级.与图4 类似,图8 中y+=[90,700]区间内涡旋密度与壁面距离也呈对数关系,lgΠ=−1.7×10−3y+−3.14,拟合相关系数R2=0.999 6,可能由于壁面和水面的影响,导致这两个区域内关系不符合对数律.

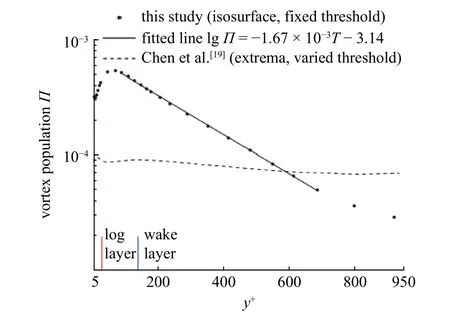
图8 壁面距离对涡旋提取密度的影响Fig.8 Influence of wall distance on the number of extracted vortices

图8 还对比了本文定阈值结果与已有文献变阈值结果,其中Chen 等[19]采用变阈值方法提取涡旋,将大于(平面内旋转强度的均方根)的局部极大值点选出,且仅当其周围8 个点同时大于时定义为涡旋.可见,两条曲线差异较大,定阈值曲线快速递减(极大值是极小值的10 倍以上),而变阈值曲线缓慢递减(极大值仅是极小值的1.5 倍左右).此外,当y+＜ 580,定阈值涡旋密度大于变阈值,而当y+＞ 580,定阈值涡旋密度小于变阈值.原因主要有两点: (1) 变阈值的在近壁区大于定阈值0.04,而在外区小于0.04;(2) Chen 等[19]用9 点法筛选涡旋(与2.1 节一致),而本文基于等值面体的提取方法捕捉涡旋,所以造成两者的结果差异较大.

图9 给出了壁面距离对涡旋形状因子概率函数的影响.总的来说,图9 与图5 存在很多相似之处,都是随着自变量(阈值或壁面距离)的增大,因变量(4 个参数)的PDF 或CDF 逐渐重合.涡旋形状因子的概率函数在不同分区内表现的不同,以缓冲层内最为显著.随着壁面距离的增加,对于圆度因子,PDF 曲线从右偏变为左偏分布,众数从0.4 变为0.9;对于半径因子,PDF 曲线右偏分布,缓冲层内曲线较为平坦,众数位于[15,30]范围,对数区与尾流区曲线高耸且基本重合,众数在8.5 附近;对于纵横比因子,PDF 曲线在缓冲层内右偏分布,众数约0.2,在对数区及尾流区内接近无偏分布,众数约0.5;对于凸状因子,从缓冲层到尾流区,数值分布区间逐渐变窄并向1 靠近,各垂向平面的CDF 曲线与图5 中相应比例阈值下的曲线基本一致.

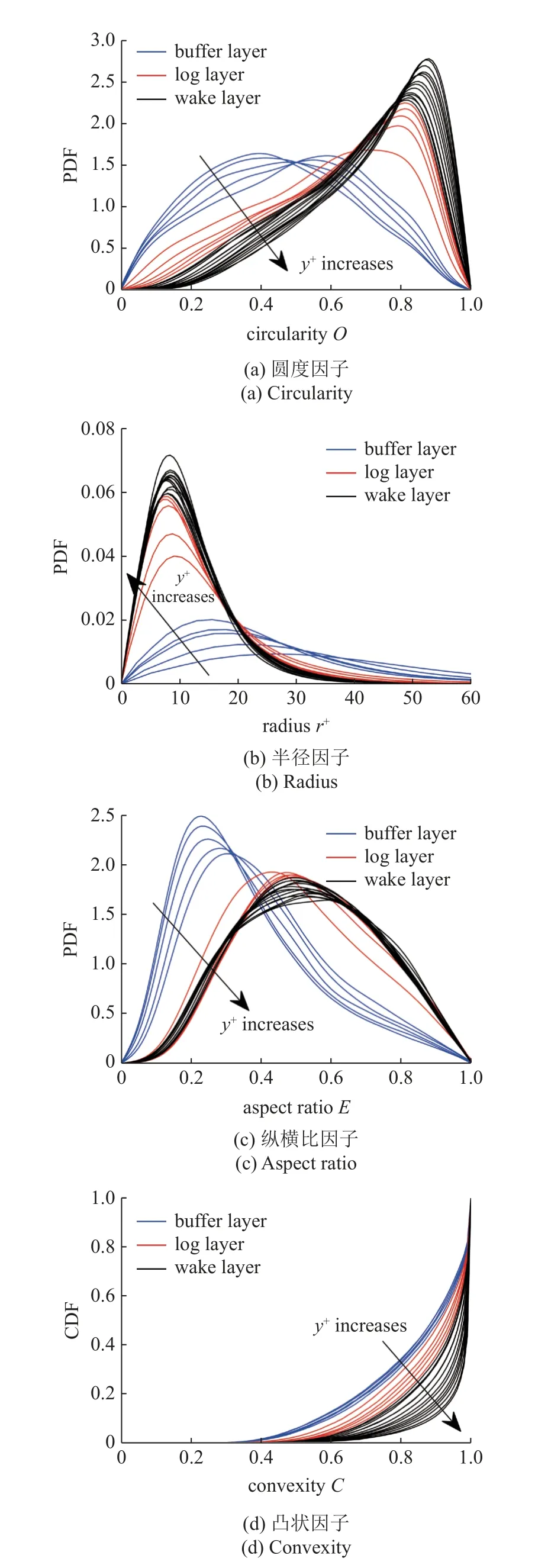
图9 壁面距离对涡旋形状因子概率函数PDF 及CDF 的影响Fig.9 Influence of wall distance on PDFs and CDFs of vortex shape factors

图10 给出了壁面距离对涡旋形状因子均值的影响.随着壁面距离的增加,圆度因子均值不断增加(从0.43 增至0.74),但增速在缓冲层与对数区内较大,在尾流区内较小.

图10 壁面距离对涡旋形状因子均值的影响Fig.10 Influence of wall distance on mean values of vortex shape factors

与圆度因子类似,凸状因子均值也随壁面距离增加而增大(从0.84 增至0.96),增速也是先大后小,但数值上各区差异不大;纵横比因子均值在y+=[5,70]区间内快速递增,从0.35 增至0.54,此后基本维持不变;半径因子在y+=[5,140]区间内快速递减,从15 减至11.5,此后基本保持稳定.

缓冲层内以准流向涡为主,倾角(涡管轴向矢量与xz面夹角)一般以10°～20°为主;对数区内发夹涡逐渐产生,并在尾流区内成为主要的涡结构,倾角主要以45°为主[3,30].由于缓冲层内涡旋结构倾角很小,相比其他两个分区,涡管切面的多边形更狭长,所以缓冲层内计算的圆度、纵横比因子数值都较小,而半径因子数值较大.

图10(b)给出了本文定阈值结果与已有文献变阈值结果的对比,其中Herpin 等[22]和Chen 等[19]都采用变阈值方法提取涡旋,将大于(平面内旋转强度的均方根)的局部极值选为涡旋中心,不同的是,Herpin 等[22]利用Oseen 涡模型拟合获取涡旋半径,而Chen 等[19]采用区域生长算法提取涡旋边界并计算涡旋半径.可以看出,Herpin 等[22]和Chen 等[19]由于采样相同的变阈值,所以涡旋半径都是随壁面距离增大而增加的,差异仅是数值而已.本文采用定阈值得到涡旋半径随壁面距离先减小(与准流向涡角度有关)后保持不变.可见定阈值和变阈值得到的规律完全不同,已有的变阈值结果会让读者造成误解,认为涡旋半径随壁面距离增大,其实如果阈值相同,涡旋半径全域几乎不变.

3 结论

本文基于涡旋等值面体研究了阈值与壁面距离对涡旋形状因子的影响.主要通过旋转强度提取涡旋信息场,利用移动立方体算法快速生成某阈值下的涡旋三维结构等值面体(以三角网格为单位),设置三角形切面,通过两三角形相交快速检测算法提取两者的切线,结合涡旋物理属性提取涡旋多边形,由此计算涡旋形态因子(圆度、半径、凸状及纵横比因子),并通过概率函数曲线与统计均值的变化,研究阈值与壁面距离对涡旋形状因子的影响规律.值得指出的是,本文研究结论是在单一雷诺数条件下获得的,其他雷诺数下的结果可能有一定的差异.本文得出主要结论如下.

(1)相比基于区域生长算法等的传统涡旋提取方法,基于涡旋等值面体并利用切面法提取涡旋的方法,可以更精确地捕捉出接近网格尺度的涡旋,得出更符合物理意义的涡旋形态参数统计规律.

(2)量化了对数区y+=110 平面内阈值范围条件下涡旋数量及形状参数的变化规律.对于涡旋密度,阈值越大,涡旋密度越小,两者呈对数关系 lgΠ=−8.25T−1.67.随着阈值的增加,对于圆度因子,其PDF 曲线由平坦变得高耸,均值先增加随后基本在0.65 附近波动,表明涡旋不断变得更圆随后保持类圆形态;对于半径因子,其PDF 曲线簇变化规律与圆度因子相似,但均值不断减小;对于纵横比因子,其PDF 曲线未显著改变,均值在0.5 附近波动,表明涡旋外接椭圆长、短轴比值约维持为2;对于凸状因子,数值分布区间逐渐变窄并向1(类似脉冲函数)靠近,说明涡旋逐渐变得饱满.

(4)阐明了全域定阈值与变阈值条件下涡旋数量与半径变化规律的差异.对于涡旋密度,定阈值与变阈值结果都随壁面距离先增大后减小,但变阈值导致涡旋密度在尾流区衰减不符合对数律.对于变阈值,已有文献中涡旋半径随壁面距离增大而增加;对于定阈值,涡旋半径随壁面距离快速减小(与流向涡有关)后基本保持不变.这种人为刻意的沿壁面距离变阈值的涡旋属性提取的结果,“扭曲”了我们对真实三维涡旋结构的理解,误认为在远离壁面的过程中涡核会变大.其实只要阈值一定,涡核尺寸就维持不变,远离壁面的过程中只是高能涡旋不断破碎并将传递能量给低能涡旋,减小的只是高能涡旋的数量.