可变重心线路巡检机器人摆振分析及抑制
樊 星, 李小彭, 彭健文, 刘炳斐
(东北大学 机械工程与自动化学院,沈阳 110819)
为了确保高效可靠的电力供应,输电线路需要定期巡检,以便及时发现诸如:腐蚀和机械损坏等线路故障,以避免不必要的经济损失[1]。传统的人工线路巡检方法存在安全性、经济性等的不足,而机器人进行线路巡检成本更低、速度更快、安全性更高[2],成为各地学者与研究机构的研究热点。目前的研究主要集中在构型创新设计[3],电力检测识别[4],动力学及动态性能分析[5-7],控制系统等方面[8],而在巡检机器人振动分析与优化方面研究较少。
考虑到巡检机器人野外的工作环境的特殊性,所以机器人本身对外界自然现象(如:风、冰、雨等)较为敏感,特别是在自然风影响下,机器人会出现风振摆动的情况。这不仅会影响巡检质量,严重时甚至会造成机器人脱线。因此开展风载荷影响下巡检机器人的摆振分析及抑制具有十分重要的工程意义。为此,国内外研究机构已在此领域已开展了一系列的研究,包括:研究配备传感器对机器人所受风速与风向进行测量[9];提出建立弹簧阻尼系统的巡检机器人模型,分析外部扰动对系统的影响[10];以及风载影响下机器人抓取稳定性的研究[11]。还有一些其他研究团队在风载对张力塔—输电线系统的影响方面进行了一些研究[12-13]。但是上述研究中仅做了相关理论分析,缺少针对现有的巡检机器人开展进一步的抑振优化策略研究,而这对机器人能否稳定巡检具有十分重要的工程意义。
在振动系统附加动力吸振器已成为常见的减振方式,其原理为在受激励的主系统上附加吸振器系统从而有效抑制主系统的振动,是一种有效、可靠和低成本的被动减振策略。有关动力吸振器的研究最早可追溯到100年前Frahm[14]设计的无阻尼吸振器,后来Ormondroyd等[15]在其基础上引入阻尼,扩大了吸振器的可用范围。经过不断优化改进研究,目前动力吸振器已广泛应用于交通运输、工业机械、建筑桥梁等工程实践中,成为振动控制领域重要措施之一[16]。在动力吸振器的诸多研究中,由于平面摆模型常被用于模拟如较高建筑物,机器人手臂,索道缆车摆动等实际工况,因此摆式吸振器的研究在不同领域,如:机械、交通、土木中均发挥着越来越重要作用[17]。有关摆式吸振器的研究最早可追溯到1995年Matsuhisa等[18]开展的对索道运输设备安装不同类型动力吸振器的理论分析。后来La[19]进一步开展了一系列摆式吸振器参数优化与结构改进等方面的研究,Viet[20]提出一种利用科里奥利力减弱摆式机构振动的动力吸振器,开展了吸振器的最优参数研究及半主动控制;Furtmüller等[21]提出了一种通过流体实现摆式机构的低频振动控制的动力吸振器;Nguyen[22]利用等效黏性阻力最大化法开展了二自由度倒立摆吸振器的参数优化;但是以上研究多偏向于吸振器理论分析,考虑到巡检机器人工作环境的特殊性以及很少有学者结合具体工程工况开展吸振研究,开展动力吸振器在巡检机器人工程实践中的应用研究具有重要的意义。
本文的目的是针对可变重心线路巡检机器人在工作中易受风扰动影响出现摆振的问题。基于摆式动力吸振器的工作原理及可变重心线路巡检机器人的结构特点,提出一种在机器人的重心调整箱体中加装动力吸振器的抑振策略。首先,对巡检机器人工作的架空输电线系统、吸振器结构进行描述,确定具体工况参数。基于Davenport谱建立了风扰动模型,确定了后文分析的具体风力数值。分析了机器人行走对输电线的影响,建立了机器人摆动的动力学模型,仿真了不同风速影响下机器人的风振响应。建立巡检机器人加装吸振器后的动力学方程,完成了吸振器的参数设计,并对比加装吸振器与否对巡检机器人风载荷下振动响应的情况。最后通过试验验证了所提出结构改进抑振策略的有效性及可行性。
1 系统描述
1.1 架空输电线系统
可变重心线路巡检机器人在输电线环境中受风载影响示意图,如图1所示。

图1 输电线巡检机器人巡检工作图Fig.1 Diagram of a PTLIR in inspection
由图1可知,研究对象可变重心巡检机器人整机由两个关节臂与连接部件组成;连接部件则由机架与重心调整箱体组成。其中,重心调整箱体主要用于越障时机器人的重心调整,而在正常巡检时是固定不动的[23]。此外,由图1可知输电线巡检机器人工作环境特点为:野外自然环境作业、作业高度距离地面一般为几十米的高空。
野外环境中受自然环境因素(如:风、冰雪、气温等)会影响机器人的工作性能,其中对机器人影响最大、最具有研究意义的为风扰动。当巡检机器人在架空线路上工作时,作用在机器人机体上自然风扰动会导致机身的摆动,极大地影响机器人行驶的安全性与巡检数据的可靠性。为方便研究,本文首先依照我国架空输电线特点,确定在研究中机器人所在高度为35.125 m[24]。并进一步确定研究中具体导线型号为LGJ-630/45,张力为35 316 N,弧垂16.5 m,档距400 m[25]。
1.2 摆式动力吸振器结构描述
考虑到可变重心线路巡检机器人自身的结构特点,本文提出在重心调整箱体加装动力吸振器的抑振策略,具体结构如图2所示。
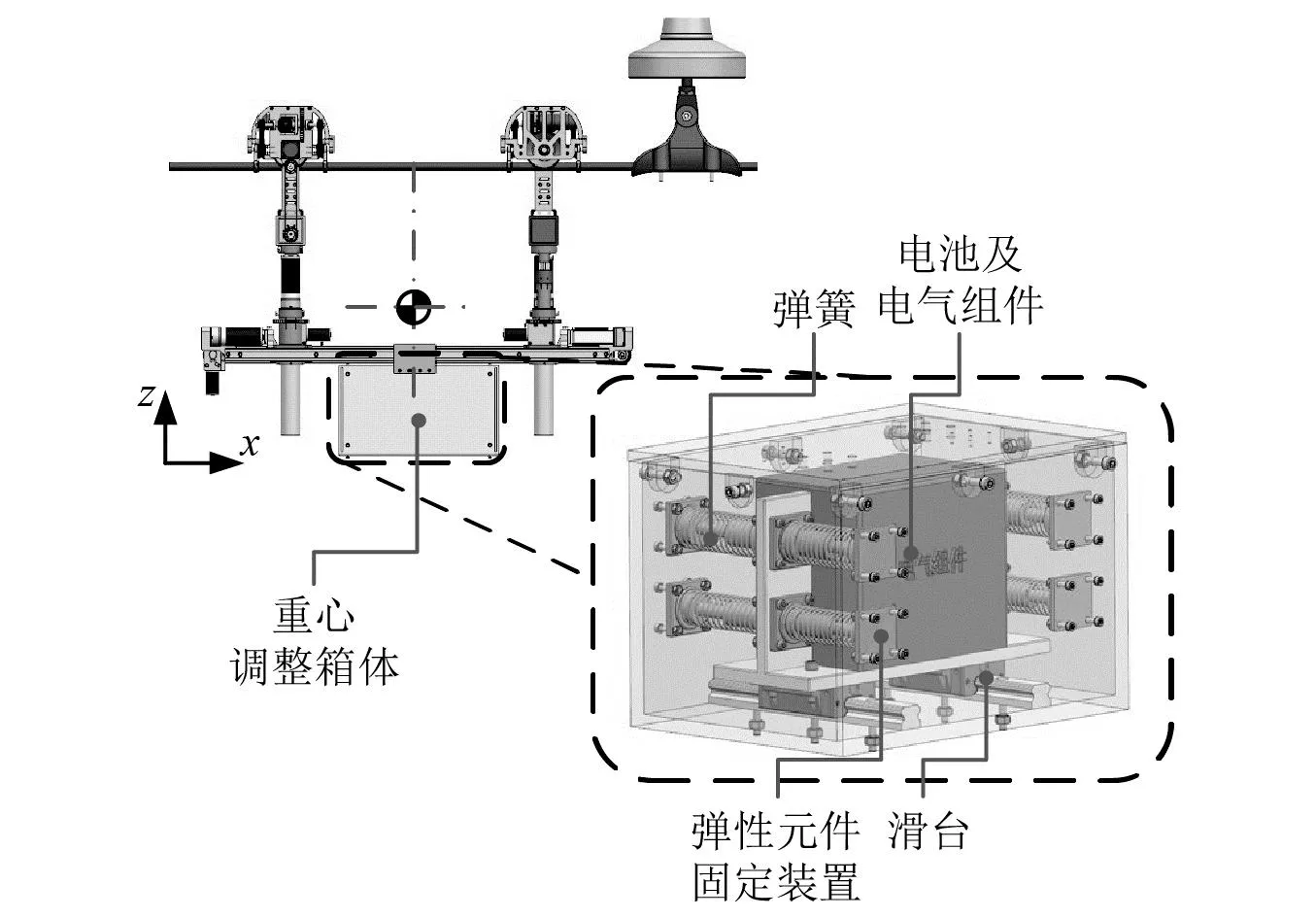
图2 重心调整箱体加装吸振器的结构图Fig.2 Structure drawing of center of gravity adjustment mechanism with DVA
在工程实践中动力吸振器中常用的弹性元件有扭转弹簧、压缩弹簧、卷簧、板簧等;阻尼元件有电磁阻尼、摩擦阻尼、磁性阻尼、液压阻尼等。所设计的动力吸振器中弹性元件使用压缩弹簧,阻尼元件使用滑台。图2中原本固定在箱体的电池及电气组件被作为吸振器的质量块固定在滑台上,作为吸振器的吸振质量。
2 风扰动模型
当巡检机器人在输电线上开展巡检工作时,风的扰动是其主要的外部干扰,具体表现为作用在机器人机体上均匀分布的力。风力大小主要由风速决定。
根据Davenport的标准理论,自然风速为平均风速与脉动风速的组合,计算公式为
v(z,t)=vm(z)+vg(z,t)
(1)
式中:z为高度值;vm(z)为高度为z的平均风速值;vg(z,t)为脉动风速,具有时变性的特点。
2.1 平均风速
由于不同地貌对自然风速的阻碍不同,所以不同高度下风的速度也不同。在正常地形中,风速随着高度增加而增加。
平均风速与高度的关系可以表示为
(2)
式中:zs为参考高度;vs为离地参考高度zs处的平均风速;α为地面粗糙度系数。
对于地面粗糙度系数α,由式(2)可知,不同地面粗糙度系数α下,平均风速剖面也不一样[26]。依据我国规范将地面粗糙度分可为4类,表1给出了每类情况下对应地面粗糙度系数α数值。进一步可得平均风速剖面曲线如图3所示。由图3可知,当已知标准地面粗糙度具体类别α在标准参考高度zs处的平均风速vs后,则可由式(2)确定某一高度z处平均风速的大小。

表1 地面粗糙度指数表Tab.1 Ground roughness index table
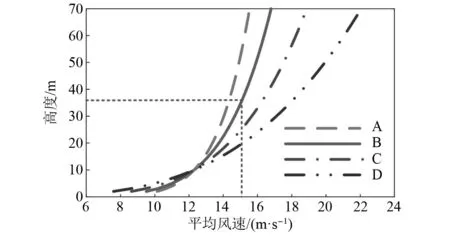
图3 平均风速剖面Fig.3 Steady-state wind speed
根据输电线环境,可确定本文研究参考地面粗糙度系数α为0.16。此外,因我国对地面气象信息一般通过高度为10 m的气象观测塔采集,所以其参考高度zs为10 m。依据所确定的输电线高度,机器人工作高度z定为35.125 m,参考表2的风力等级表计算得到本文所选定的可能的平均风速的最小、最大风速计算分别如式(3)与式(4)所示。

表2 风力等级表Tab.2 Wind scale
(3)
(4)
2.2 脉动风速
脉动风是一个均值为零的平稳高斯随机过程,通常用随机振动理论进行分析。
Davenport进行了大量的风洞试验,给出了一个广泛应用的风频谱,它取决于平均风速和地形粗糙度。Davenport谱可以表示为
(5)
式中:β=Lvf/vm,Lv为湍流尺度;f为脉动风频率;k为表面阻力系数(0.005≤k≤0.015)。
通过将单位标准差的白噪声信号输入Davenport谱的近似滤波器可得脉动风速。本文采用的滤波器为三阶,具体传递函数如式(6)所示。
(6)
依据上述步骤绘制用以描述脉动风速的时程曲线,结果如图4所示。
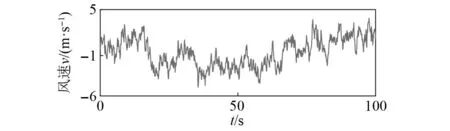
图4 风速的时程曲线Fig.4 Wind speed time history curve
2.3 风力计算
分析巡检机器人在风场中受到风扰动作用对机器人稳定性的影响时,首先需要获得风力大小。由于风速相对较易测得,因此可先确定风速大小,然后通过将风速转化为风压,最后得到风力。
依据伯努利方程,得到的风压与风速的表达式为
(7)
式中,ρa为空气密度,ρa=γ/g,g,γ分别为重力加速度和容重。按标准大气压有g=9.8 m/s2、γ=12.018 N/m3。
进一步得到对应风力的计算表达式为
(8)
式中:C为阻力系数;A为机器人迎风方向的截面面积。
考虑到受风载影响时,不同机身结构下阻力系数C不同。将机器人-输电线系统分为3个部分具体如图5所示。
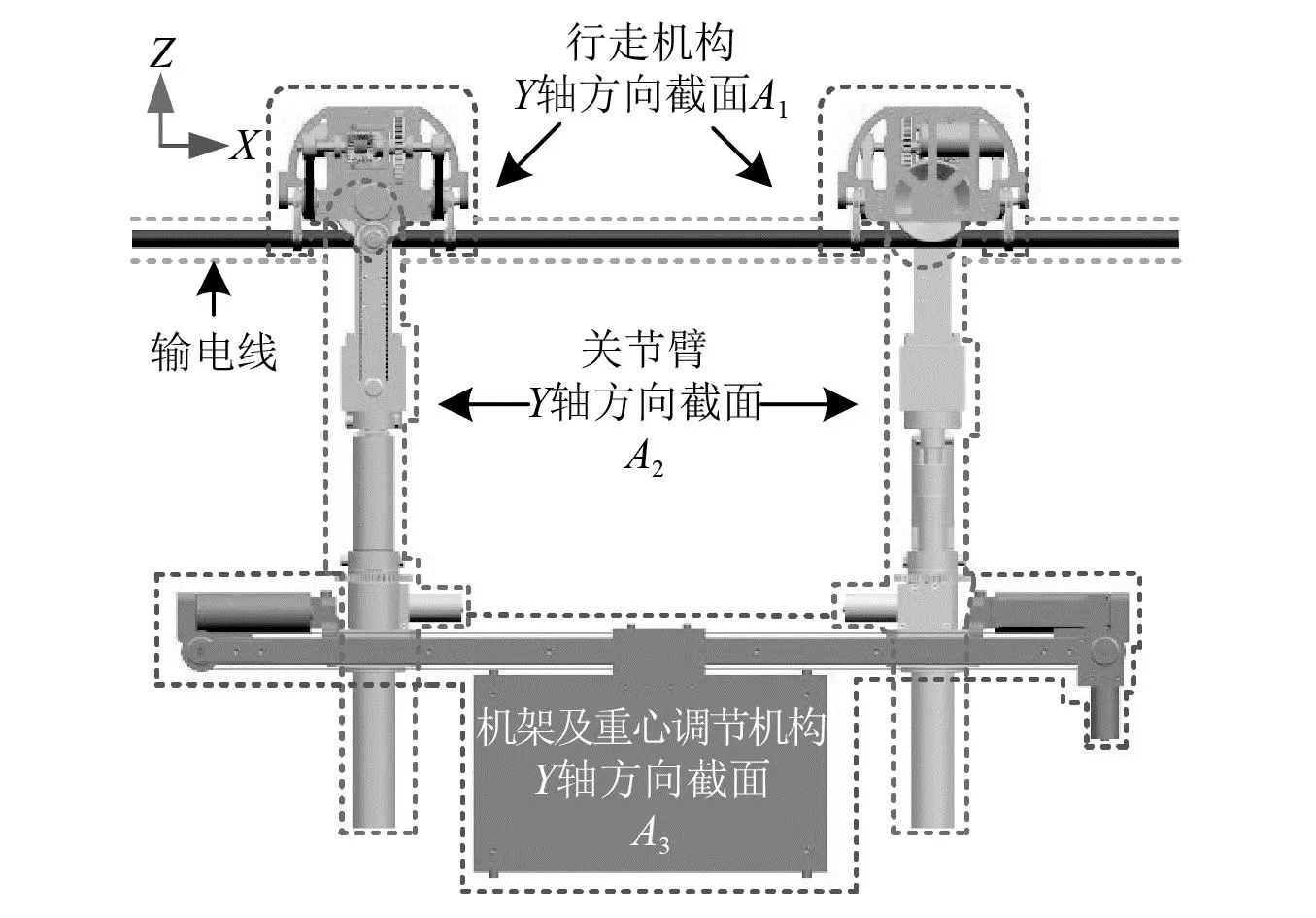
图5 风扰动影响下巡检机器人的截面图Fig.5 The cross section of the PTLIR under the influence of wind disturbance
图5中:Ai为机器人-输电线系统的不同位置在Y轴方向的横截面积;Ci为对应的阻力系数;参数具体数值如表3所示。

表3 模型参数Tab.3 Modelling parameters
基于以上分析过程,本文风力计算模拟过程如图6所示。风扰动影响下的风力计算表达式如式(9)所示。
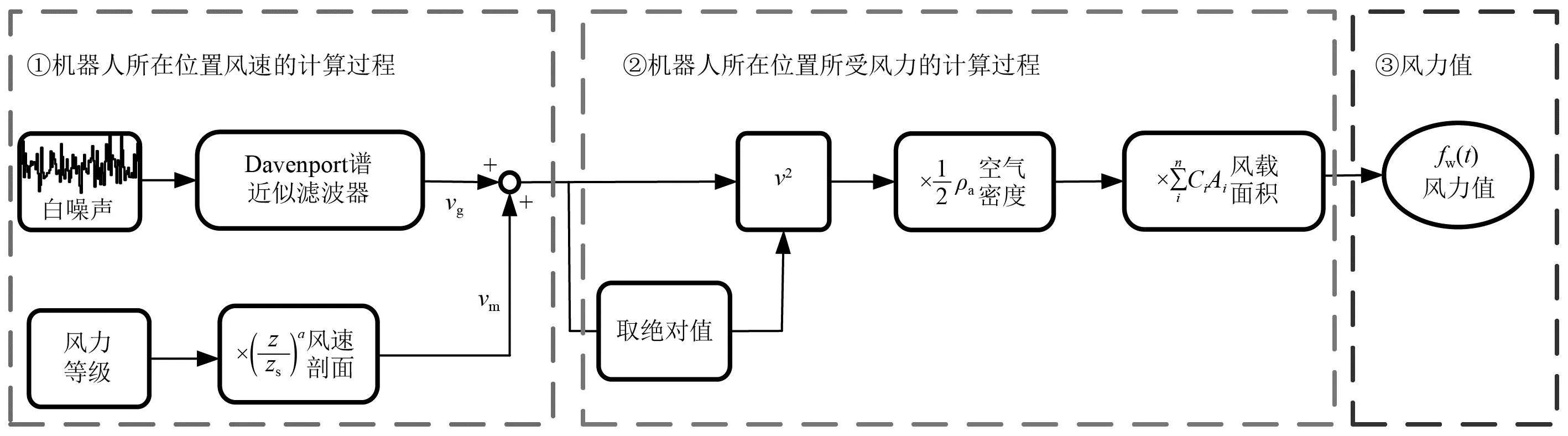
图6 风力计算流程图Fig.6 Flow chart of wind force calculation under natural wind
(9)
进一步绘制的风载荷的时变曲线图如图7所示,可用于下文后续研究中模拟风力。
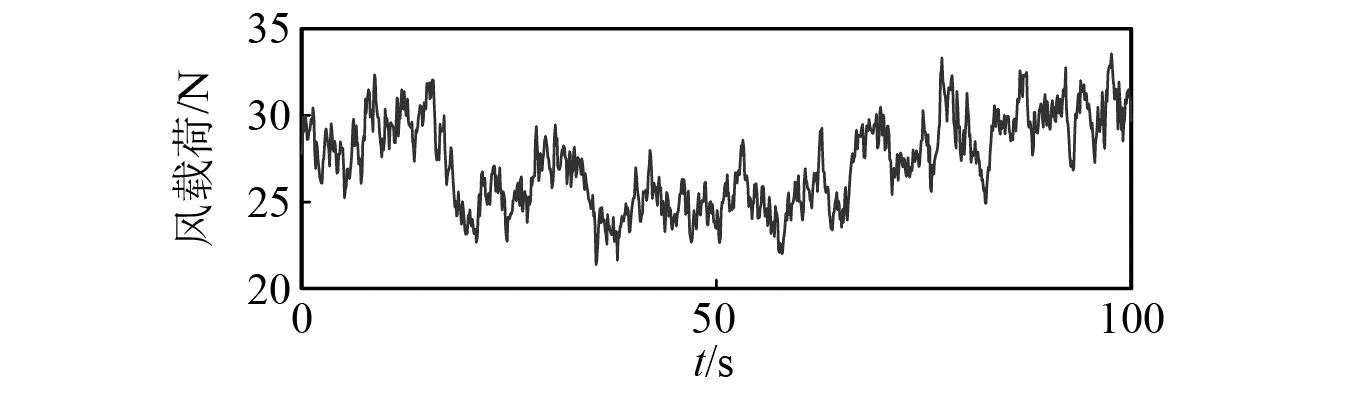
图7 机器人所受风载荷的时变曲线图Fig.7 Time varying curve of transverse wind load on robot
3 风扰动影响下机器人摆振分析
3.1 机器人摆动的动力学模型
考虑到机器人在行走状态下进行巡检时是作为一个移动的负载作用在输电线上,从而引起输电线的振动。因此如图8所示,将输电线视为一根拉伸的弦,将在输电线上执行巡检任务的机器人视为线上行走的移动负载。
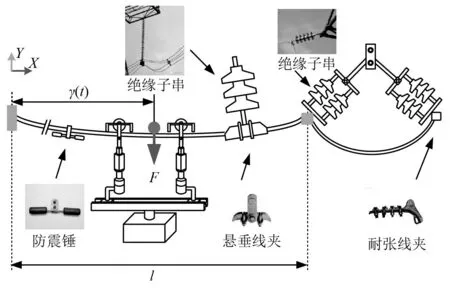
图8 行走状态下巡检机器人示意图Fig.8 Schematic diagram of inspection robot in walking state
建立弦的横向振动方程如式(10)所示
(10)
式中:ρ为弦的单位长度质量,ρ=ρ(γ);f为作用在弦上的横向分布力;T为张力,T=T(γ,t);L为线的跨长;u为弦γ处的横向位移,u=(γ,t)。
由图可知,输电线在两端的位移为0,从而可得边界条件及初始条件如式(11)所示
(11)
考虑到巡检机器人作用在输电线行走时,输电线受到机器人作用的力是移动的,可用狄拉克函数表示。如式(12)所示为机器人重力作用在所在位置γ处输电线上的力。
f(γ,t)=F(t)δ[x-ε(t)]
(12)
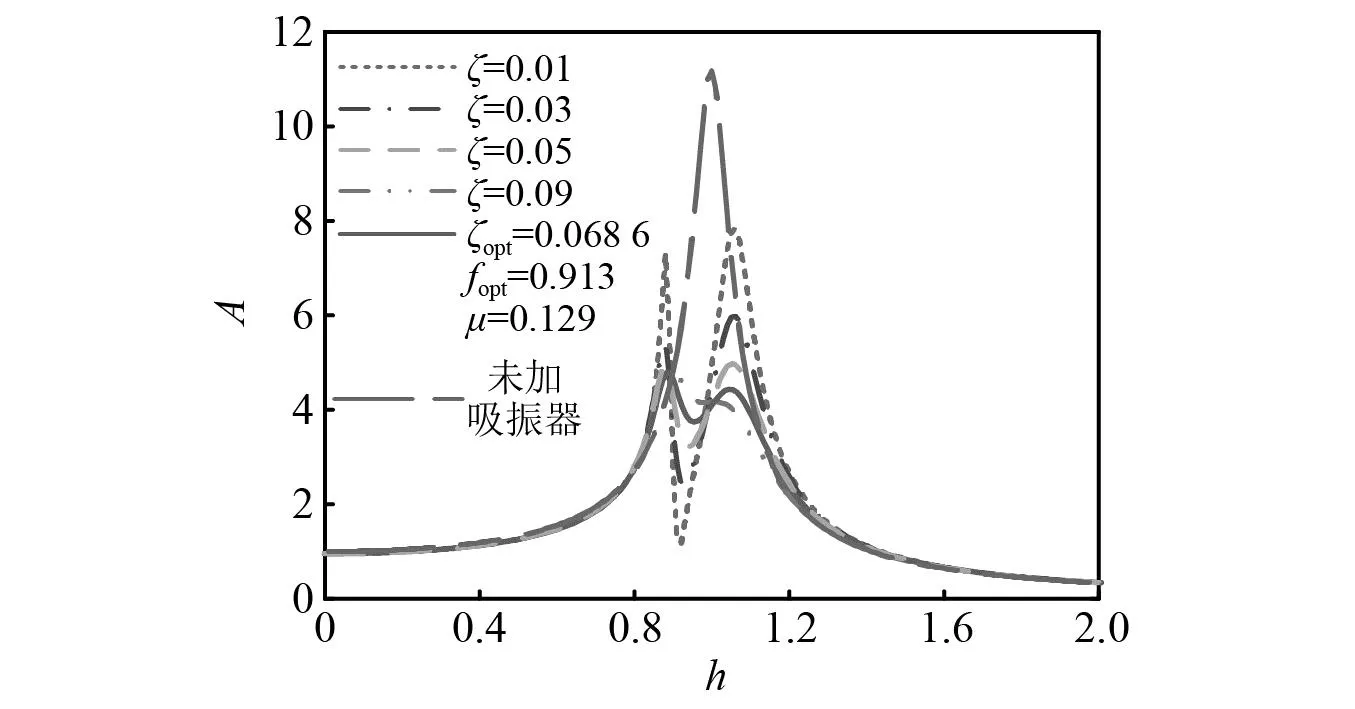
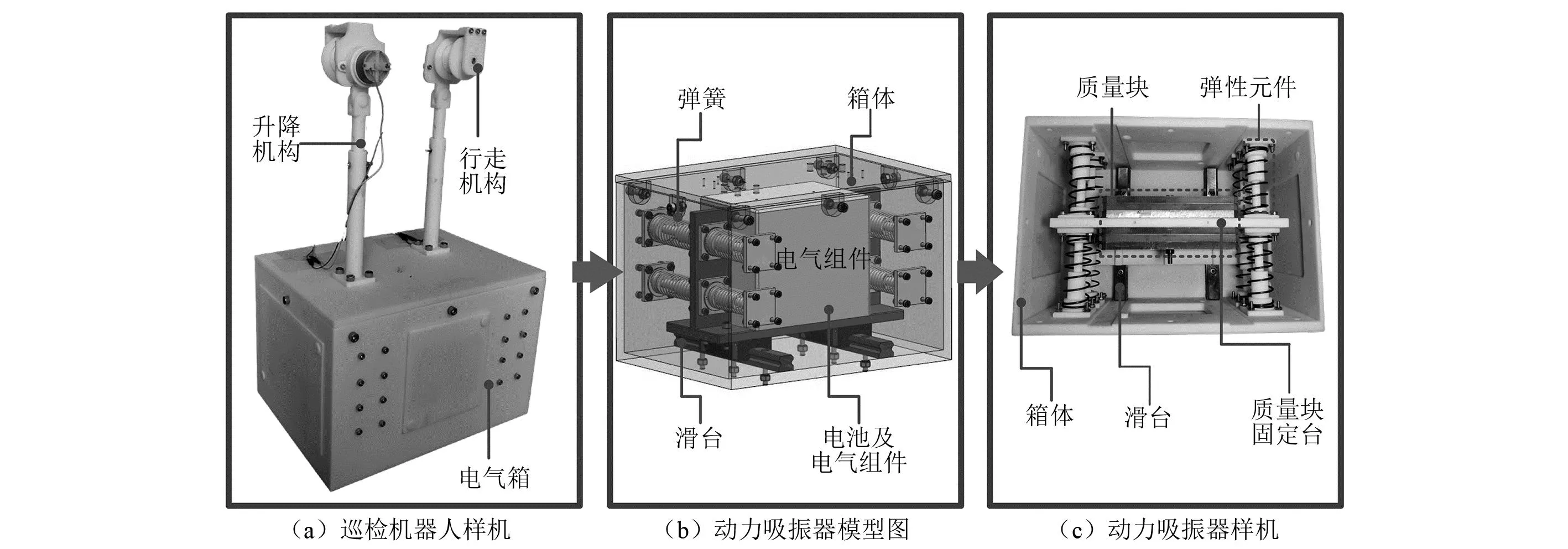
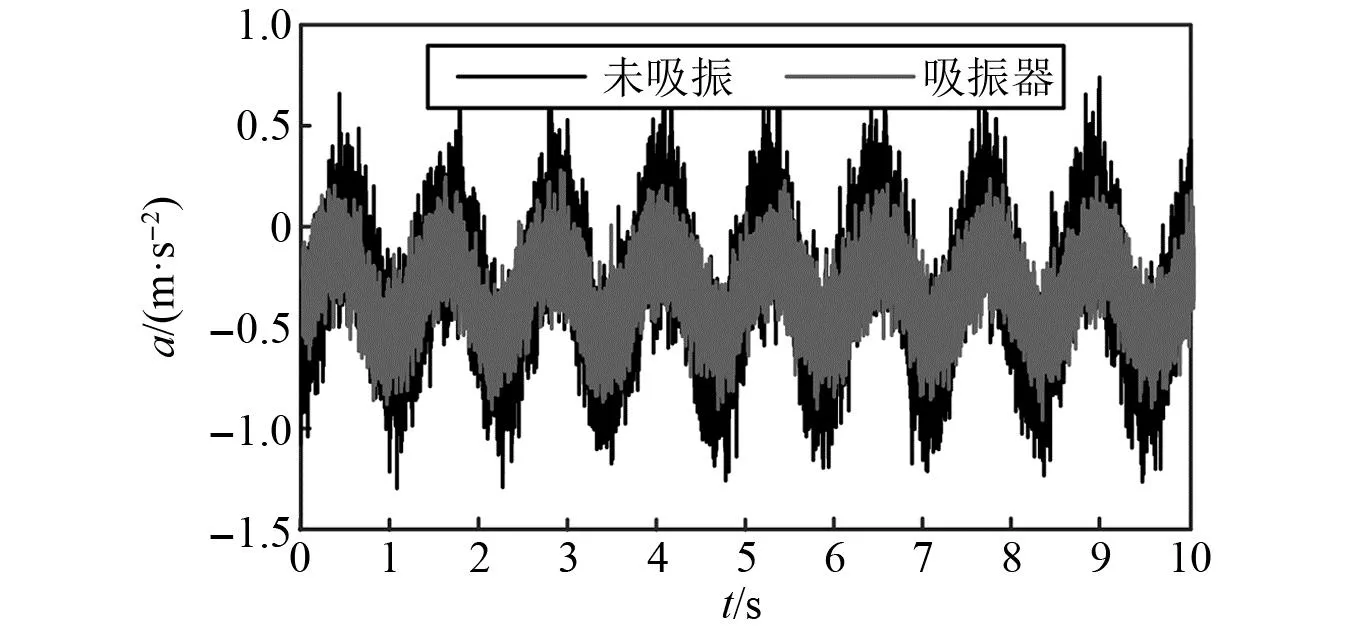
式中,移动的巡检机器人移动规律函数ε(t)的限制条件为0 对式(10)的求解可以用式(13)所示的拉格朗日方程 (13) 输电线作为弦的动能与势能如式(14)所示 (14) (15) 使用零初始条件下的杜哈梅积分求解上述方程,得到方程的解如式(16)所示 以选择导线的型号为LGJ—630/45的输电线路导线为对象进行分析计算。仿真结果如图9所示。 图9 输电线挠度及加速度变化Fig.9 Deflection and acceleration changes of transmission lines 由图9可知,巡检机器人在无障碍行走状态下进行输电线巡检任务时,输电线受机器人移动的影响,挠度变化呈现正弦运动,并伴有锯齿状振荡。且当机器人行走到输电线中心处时,输电线的挠度变化最大,大小约为0.5 m。对比输电线因自身重力作用下产生的弧垂16.5 m,该挠度变化较小,在此期间导线振动波动加速度范围为-1.5×10-3~1.5×10-3m/s2,该数值也较小,因此在后文研究中对机器人行走对输电线影响予以忽略处理。 此外,由于输电线上有安装具有传递机械载荷、保护输电线路的线路金具,如:防震锤、间隔棒等。因此为便于研究,下文所开展的对机器人风载稳定性影响研究中,对因风载引起的输电线舞动予以忽略处理。 巡检机器人在进行线路巡检时,通过行走轮与输电线接触,挂立在输电线上行走巡检。因此,当其受风载影响时,可假设模型为如图10所示的巡检机器人单摆模型图。 图10 风扰动下巡检机器人的摆动模型Fig.10 Swing model of PTLIR under wind disturbance 如图10所示,当横向风载荷fw(t)作用在总质量为m的巡检机器人上,机器人将受力倾斜,受风载荷fw(t)与重力作用,建立如图所示摆长为l1的单摆模型,用ψ(t)表示机器人的摆动角度。 建立动力学方程如式(17)所示 (17) 式中:M为行走机构处的阻力矩;c1为阻尼系数;J为机器人的转动惯量。 为便于分析,假设巡检机器人受风载影响的摆动角度不大[27],则有sinθ≈θ,则式(17)可简化为 (18) 对其进行Laplace变换,得到如式(19)所示的机器人受风载影响摆动的系统传递函数。 (19) 由式(12)仿真式(3)与式(4)已确定的风速范围内巡检机器人风载摆动响应,所得机器人摆角与摆动速度的结果分别如图11与图12所示。此外,不同风速下风激振动摆动角、摆动速度与摆动加速度的极值如表4所示。 表4 不同风速下风振摆动角的极值Tab.4 Extreme value of oscillation angle under different wind speeds 图11 不同风速下机器人的风振摆角Fig.11 Wind induced vibration angles of a PTLIR for different wind velocities 图12 不同风速下机器人的风振摆动速度Fig.12 Wind induced vibration speeds of a PTLIR for different wind velocities 根据结果,归纳可得以下结论: ① 更大风速下机器人的摆角更大,摆动速度波动程度变大,摆动加速度波动变大; ② 风速在大约小于10 m/s下机器人受风载荷影响表现为左右摆动,在风速高于10 m/s后机器人摆角偏向单侧且摆动角度过大; ③ 考虑到在风激振动下过大的摆角会造成机器人机体的不稳定,影响机器人巡检质量,因此需要对巡检机器人进行摆振抑制减小其受自然风的影响,从而保证机器人巡检的安全性。 风扰动下加装吸振器的巡检机器人摆动模型如图13所示。其中加装动力吸振器改进后重心调整箱体的结构具体如1.2节所描述,图中原本固定在箱体的电池及电气组件被作为吸振器的质量块固定在滑台上。 图13 风扰动下加装吸振器的巡检机器人摆动模型Fig.13 Swing model of PTLIR with DVA under wind disturbance 此外,图13中悬挂在输电线上的机器人被简化为质量为m1的单摆,假设其受风力影响偏离中心ψ。未装吸振器前机器人重心距离输电线中心的距离为l1,作为动力吸振器质量块的电器组件重心距离输电线中心距离为l2,电气组件质量为m2,弹簧的弹性系数为k,阻尼系数为c,在受风力fw(t)影响后吸振器质量(电池及电气组件)m2偏离原来位置距离为u(t)。 建立如图13所示的原点O位于输电线中心的坐标系,得到机器人主系统的重心坐标(x1,y1)与吸振器质量块的重心坐标(x2,y2)数值表达式如式(20)所示 (20) 对式(20)求导可得主系统与吸振器质量块的速度值,如式(21)所示 (21) 进一步计算加装动力吸振器后系统的动能,势能与保守力函数分别如式(22)~式(24)所示 (22) (23) (24) 利用拉格朗日法建立动力学方程,拉格朗日方程的表达式如式(25)所示。 (25) 将式(22)~式(24)代入式(25)的拉格朗日方程得到 (26) (27) 为方便获得频率方程,将其改写为如式(28)所示的矩阵形式 (28) 为获得系统的状态空间方程,进一步简化为式(29)所示的形式 依据建立加装动力吸振器后的动力学模型,假设机器人系统受到风力为简谐力fweiωt[28-29],并设稳态响应可表示为 ψ=Θeiωt,u=Ueiωt (30) 进一步得到频率方程如式(31)所示 det[Z(ω)]= (k-ω2m2+iωc)-(m2gl2ω2+m2g)2 (31) 因而有 (32) 通过引入式(33)所示的符号,可将式(32)化为无量纲形式。 (33) 式中:μ为质量比;Ω与ζs分别为机器人系统的固有频率与阻尼比;ωa为吸振器固有频率;ζ为吸振器的阻尼比;r为吸振器的位置参数;h为激励频率比,即激励频率与主系统的固有频率比;f为固有频率比;Θst为激励的无因次振幅。 如式(34)所示,得到了包含上述无量纲参数的形式。由式(34)可知机器人主系统的振幅是μ,ζ,h,f的函数。 (34) 式中各参数具体值如式(35)所示 A1=f2-h2,B1=2h, C1=(1-h2)(f2-h2)-u(rf2-1)(rh2-1), D1=2h(1+μr-(1+μr2)h2) (35) 使用固定点理论[30],可以得到以下最优参数 (36) 式中:fopt为最优固有频率比;ζopt为最优阻尼比,通过对p,q定点阻尼比取均值得到。p,q下的激励频率比可通过式(37)计算得到。其余各参数具体值如式(38)所示。 (38) 依据本文研究对象双臂输电线巡检机器人的实际参数,确定质量比μ=0.129;主系统阻尼比ζs=2.5。 进一步应用式(36)计算研究中确定的动力吸振器无量纲参数fopt=0.913,ζopt=0.686,仿真可得最优参数下,不同阻尼比参数下以及未加吸振器情况下的幅值曲线,如图14所示。由图14可知,吸振器的有效减振频带[31]为0.117 2。此外,由于最优固有频率比的近似计算值小于理论值,导致幅频曲线存在不等高,但仍在可接受范围内,基本实现了优化目标。 图14 不同情况下的幅频响应曲线Fig.14 The amplitude-frequency curve under different conditions 依据Davenport谱,施加随机风力样本。分别仿真自然风在平均风速为5 m/s,10 m/s和15 m/s下,机器人优化结构前及加装吸振器结构优化策略下机器人风激振动过程。结果如图15与图16所示。 图15 吸振优化前后的机器人的风振摆角对比Fig.15 Comparison of wind induced vibration angles of robot with and without DVA 图16 吸振优化前后的机器人的风振摆动速度对比Fig.16 Comparison of wind induced vibration speeds of robot with and without DVA 不同风速下优化前后机器人摆角的最大、最小值对比,如表5所示。同时,为了更直观分析抑振策略的作用效果,对比抑振前后不同风速下机器人摆角均方根值如表6所示。 表5 不同风速下机器人摆动角极值对比Tab.5 Comparison of extreme value of robot swing angle under different wind speeds 表6 不同风速下机器人摆动角均方根值对比Tab.6 Comparison of mean square root values of robot swing angle under different wind speeds 由图可知,在不同风速下加装吸振器后机器人在风载下机器人的风振摆动在摆动角ψ、摆动速度v方面均有一定程度的减弱;由表可知,不同风速下加装动力吸振器可分别使主系统的响应衰减34.13%,19.94%与13.65%。即抑振后的巡检机器人在受风扰动影响时,可以表现出更好的稳定性;此外在风速为5 m/s时系统表现出了更好的减振效果。 为验证所设计结构的有效性,在室内开展了巡检机器人风扰动试验。首先对双臂式输电线巡检器人模型进行简化,制作如图17所示的巡检机器人样机以及重心调整箱体中加装动力吸振器的样机。通过搭建室内输电环境,并使用大功率的工业风扇模拟自然风,从而验证所提出的抑振策略对机器人稳定性的影响。 图17 巡检机器人样机及动力吸振器结构图Fig.17 Structure drawing of PTLIR and DVA prototype 室内巡检机器人风扰动试验布置如图18(a)所示。其中,工业电风扇作为风力源,风速大小通过切换风扇不同档位实现。风速具体数值通过数字风速计(GM89010)测试得到。由于机器人躯干是最容易受到外界干扰的位置,同时也是一般巡检机器人摄像装置安装的位置,因此,将加速度传感器(DH3311E)安装在机器人躯干,用于测量机器人机身的振动情况。其余用于机器人线路系统实时分析的具体参数为:①所布置输电线长度为2 m;②机器人被布置在距离地面1.5 m的高度;③由风速计测得试验所用工业风扇最大风速为5.5 m/s,最小风速为4.5 m/s;④机器人行走机构采用12 V电源,控制机器人行走速度为20 mm/s;⑤每次试验的时间为1 min如图18(b)所示,通过在滑台上安装限位装置来模拟抑振前后的机身结构,用于对比吸振优化前后对机器人机身的振动情况的影响。 图18 样机试验Fig.18 Prototype test drawing 依据加速度传感器的测试数据,经过处理获得图19与图20所示的工业风扇在最大,最小风速分别为4.5 m/s与5.5 m/s的2个不同档位下,机器人躯干的振动加速度曲线。 图19 风速为4.5 m/s下机器人躯干的加速度曲线Fig.19 Acceleration curve of robot body at wind speed of 4.5 m/s 图20 风速为5.5 m/s下机器人躯干的加速度曲线Fig.20 Acceleration curve of robot body at wind speed of 5.5 m/s 由图19、图20可知在4.5 m/s与5.5 m/s风速下,采取加装动力吸振器抑振策略的机器人,其躯干的振动情况明显减弱。即在风力等级为三级的试验环境中,加装吸振器后的巡检机器人的工作稳定性表现更好。 (1) 针对可变重心输电线巡检机器人在工作时受风扰动影响摆振现象导致稳定性变差的问题,本文提出一种基于摆式动力吸振器摆振抑制策略,并完成了结构设计及样机制作。采用拉格朗日方程建立了摆式动力吸振器的动力学模型,完成了吸振器的参数设计,通过仿真与试验验证了所提出的改进策略的有效性。 (2) 机器人行走对输电线的挠度影响变化呈现正弦运动,并伴有锯齿状振荡,在风速小于10 m/s时,机器人受风载荷影响表现为左右摆动;在风速大于10 m/s后机器人摆动角度过大,会造成机器人机体的不稳定,影响机器人巡检质量。 (3) 仿真环境中,风速为5 m/s,10 m/s与15 m/s时,加装动力吸振器可分别使主系统的响应衰减34.13%,19.94%与13.65%;室内试验环境中,在工业风扇风力等级为三级时,加装动力吸振后的巡检机器人摆振波动程度更小。即采用加装动力吸振器的抑振策略后,巡检机器人在风振响应程度方面可表现出更好的稳定性。
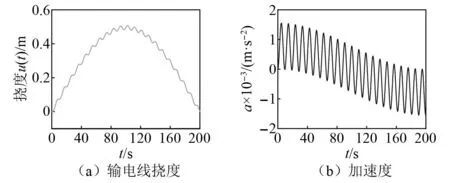

3.2 仿真分析


4 基于摆式动力吸振器的摆振抑制策略
4.1 加装动力吸振器后的动力学模型
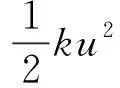
4.2 动力吸振器的参数设计
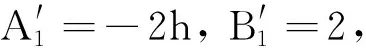
4.3 仿真分析




5 样机试验

6 结 论

