市域列车牵引变压器声辐射特性与降噪措施分析

黄佳程, 肖新标, 王 奇, 杜 星, 周顺元, 都业林

(1. 西南交通大学 牵引动力国家重点实验室,成都 610031; 2. 西南交通大学 电气工程学院,成都 610031; 3. 中车大连机车车辆有限公司 城铁开发部,辽宁 大连 116022)

市域列车运行速度介于高铁与地铁之间,其主要运营在大城市中心城区与其卫星城之间,具有快速启停的特点。较高的运行速度与快速启停的特点对市域列车牵引系统的运行功率提出了更高的要求,尤其是牵引变压器。在车体轻量化的大环境下,市域列车车体的刚度较低,凸显了牵引变压器的噪声问题。现场试验表明,在市域列车静置或低速行驶时,牵引变压器是车内噪声的主要来源之一。因此,研究牵引变压器的噪声特性显得更加迫切。

变压器工作时内部存在周期性变化的电磁场,铁心硅钢片、绕组等结构在电磁力的强迫作用下发生振动,并向周围辐射噪声[1]。为研究变压器的振动问题,国内外学者对其开展了大量试验测试与理论建模的工作。Kitagawa等[2]通过试验测量硅钢片的磁致伸缩特性,获得了磁通密度与磁致伸缩率的关系。Mapps等[3]进一步通过测试,发现硅钢片在纵向上振动大于其在横向上的振动,其具有各向异性。Moses[4]测量了由多层硅钢片组合而成的铁心的振动特性,发现铁心振动能量集中电压的偶次谐波上。汲胜昌等[5]通过测试得到了变压器铁心与绕组的振动幅值与电流电压的关系,测试仅得到了振动与电学参数在基频(电压的2倍频率)上的经验公式,并未能建立更高谐波频率上两者的对应关系。为了更深入地分析变压器铁心振动的影响因素,Michael等[6]提出需要综合考虑变压器电磁场-结构力场的耦合影响,并基于有限元法建立了铁心在电磁场-结构力场耦合作用下的仿真模型。师愉航等[7-8]通过建立模型研究了绕组和箱体的振动问题,发现绕组振动主要集中在100 Hz处,变压器箱体振动集中在100 Hz谐波频率处。祝丽花等[9]建立了包含详细内部结构的变压器模型,通过仿真指出变压器铁心的振动远大于绕组振动,后续建模时可忽略绕组的影响。Yan等[10]通过仿真分析明确了铁心振动的来源为磁场的强迫振动,即磁致伸缩效应。

对于变压器振动的影响因素,同样有大量学者开展了丰富的研究。李琪菡等[11]分析了铁芯和绕组压紧程度、负载功率因数、负载三相不平衡度、绝缘油黏度等参数对变压器振动的影响,指出绝缘油黏度对铁心振动传递影响较小,建模时可不考虑绝缘油的影响。朱叶叶等[12]通过试验得到了变压器空载、负载与功率因素等电磁学参数对变压器振动的影响。Weiser等[13]对影响铁心振动的关键因素进行了研究,铁心振动受磁通密度与硅钢片质量影响较大。Teeraphon[14]建立了三相变压器的铁心振动模型,讨论了硅钢片厚度、铁心压紧力等结构参数对变压器振动的影响。变压器的主要影响因素是铁心在磁场作用下的振动,即铁心的磁致伸缩效应,箱体、油液、绕组等结构对变压器噪声影响较小。需要考虑铁心磁致伸缩的非线性与硅钢片的各向异性的影响。

针对变压器铁心振动引起的辐射噪声问题,Michael等[15]通过仿真和试验分析,变压器辐射噪声能量的主要来源为铁心的振动,绕组与箱体的振动对其贡献较小。许庆新等[16]建立了变压器铁心声场仿真模型,利用实测的铁心表面法向加速度,计算了铁心的远场辐射噪声,但该模型的激励输入依靠试验测量,当外界输入条件变化时,必须重复进行振动试验,不利于变压器的噪声优化仿真。张雪冰等[17]等建立了变压器油箱的有限元模型,研究了铁心振动激励下的油箱振动能量的传递路径与分布状况,认为变压器顶面或底面的振动能体现变压器的振动水平,建议测试传感器尽量布置在顶面或底面。在电磁场-结构力场模型的基础上,王晓伟[18]建立了用于仿真变压器辐射噪声的变压器电磁场-结构力场-声场耦合模型,并通过试验数据验证了模型的准确性。综上所述,前人在变压器本体振动噪声方面做出了大量研究,但对于牵引变压器如何影响列车车内噪声尚未有人深入研究。

本文针对市域列车牵引变压器噪声特性,建立了用于分析市域列车车内噪声受牵引变压器影响的单向耦合模型,模型分为两部分:首先是电磁场、结构力场与压力声场耦合的牵引变压器辐射噪声仿真模型;其次建立了市域列车车内噪声仿真模型,两部分模型均利用试验数据进行了验证。本文的最后从电磁与结构两方面提出了多种变压器降噪方案,分析了降噪方案的有效性。

1 牵引变压器声辐射噪声特性分析

牵引变压器的内部结构图,如图1所示。牵引变压器作为市域列车关键电气设备,其主要是由铁心、绕组、夹件、铁轭、箱体等部件组成,并通过吊挂装置悬吊于车下。牵引变压器在工作状态下,其绕组会产生周期变化的磁场,该磁场的频率与绕组中电流的频率一致,在磁场的作用下,铁心因磁致伸缩效应而产生周期性振动,这是牵引变压器电磁噪声的主要来源。

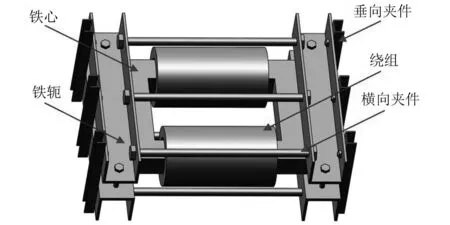
图1 牵引变压器内部结构图Fig.1 Internal structure diagram of traction transformer

1.1 牵引变压器辐射噪声试验

某型号牵引变压器的电磁噪声测试的现场图片,如图2所示。该型牵引变压器一次侧电压为25 kV,频率为50 Hz。测试时牵引变压器空载且冷却风机关闭,测点分布参考变压器电磁噪声测试标准[19],声传感器与牵引变压器箱体外轮廓之间的距离为1 m。

图2 测试现场图片Fig.2 Test site pictures

牵引变压器辐射噪声的1/3倍频程频谱图与窄带频谱图,如图3所示。其中,图3(a)给出了牵引变压器本体辐射噪声在20～12.5 kHz内的三分之一倍频程频谱数据,这是为了分析牵引变压器本体辐射噪声的声能量在频域上的分布情况,得到噪声显著频段,便于缩小噪声窄带频谱的分析范围。图3(b)给出了牵引变压器本体辐射噪声在20～1 600 Hz的窄带频谱数据。

图3 牵引变压器辐射噪声频谱图Fig.3 Radiation noise spectrum of traction transformer

由图3(a)可见,牵引变压器辐射噪声在100 Hz与200 Hz频率处存在显著峰值,噪声显著频段为中心频率在100～1 000 Hz的三分之一倍频程频带内。由图3(b)可见,牵引变压器辐射噪声在100 Hz的谐波频率处出现明显峰值,且峰值主要出现在1 000 Hz以内,其中100 Hz,200 Hz与400 Hz处的声压级分别为54.4 dB(A),60.0 dB(A)与52.6 dB(A)。由此可见,牵引变压器电磁噪声能量主要集中在1 000 Hz以内的100 Hz的谐波频率处。

1.2 牵引变压器辐射噪声仿真建模

牵引变压器辐射噪声模型分为电磁场、结构力场和压力声场三部分。

1.2.1电磁场建模

在对牵引变压器内部电磁场进行建模时,添加了外部电路,运用场路耦合法,将电磁场方程与外电路方程直接耦合联立,用于求解绕组产生的磁场。图4给出了模型仿真电路图,图4中左侧电路图为牵引变压器高压绕组电路图,右侧电路图为牵引绕组电路图,Coil1代表一次侧绕组,Coil2代表二次侧绕组,Uac代表交流电源,由交流电源向高压绕组施加的额定电压。

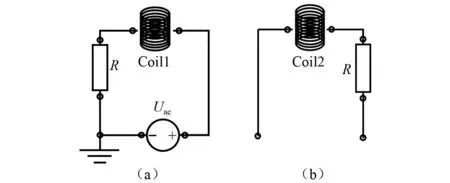
图4 仿真电路图Fig.4 Simulation circuit diagram

假设变压器一次侧电压为Umsin(ωt),由电磁感应原理可得,一次侧绕组所产生的磁感应强度B为

(1)

式中:Φ为铁心磁通量;A为铁心横截面积;N1为变压器一次侧绕组线圈匝数。

令B0=Um/(AN1ω),且B0不大于铁心的饱和磁感应强度Bs,那么铁心中的磁场强度H为

(2)

式中:μ为铁心的相对磁导率;Hc为矫顽力。

1.2.2 结构力场建模

经过电磁场计算,可以得到铁心内部的磁场强度,将其作为激励,在结构力场中计算变压器的振动。

因为绕组产生的磁场集中在铁心内部,所以夹件因磁致伸缩效应所引起的振动远小于铁心的振动,因此忽略了夹件的磁致伸缩效应,仅考虑夹件因铁心振动所引起的强迫振动。对于多层线圈绕制而成的绕组,虽然通过电流的导线之间会产生洛伦兹力,进而导致绕组振动,但由于绕组振动远小于铁心振动,所以忽略了绕组的振动。

磁致伸缩效应引起的铁心形变的计算公式为

(3)

式中:ΔL为硅钢片伸长量;L为硅钢片原始尺寸;εs为硅钢片的磁致伸缩系数。

由式(1)～式(3)可以得到硅钢片的最大伸长量ΔL为

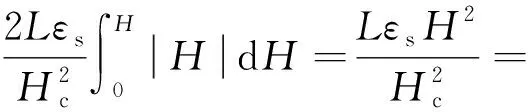
(4)

由式(4)可知,磁致伸缩效应引起的铁心振动加速度为

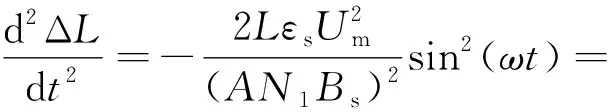
(5)

由式(5)可知,铁心振动频率为电源频率的2倍,所以由磁致伸缩所引起的铁心噪声是以两倍的电源频率为基频。

为有效仿真牵引变压器的振动,需要建立牵引变压器几何模型。牵引变压器的几何模型,如图5所示。

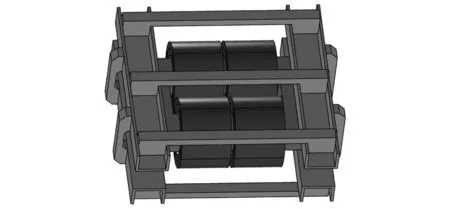
图5 牵引变压器几何模型Fig.5 Traction transformer geometric model

由图5可知,该模型主要由铁心、绕组、铁轭、夹件组成,并在建模过程中对模型进行相关简化。忽略了铁心的层叠结构,将其视作一个整体,考虑到绕组的实际结构为多圈导线绕制并使用绝缘材料压紧而成,所以将绕组简化为多个空心圆筒进行建模,对于夹件,忽略了螺栓、螺孔等局部结构的影响,通过设置边界条件的方式对各部件之间的接触关系如预紧力等进行模拟。

结构力场是为了计算铁心以及夹件的振动加速度。针对现有的几何模型,不考虑模型与箱体的约束,将模型的边界设置为了自由状态,并且考虑了各部件材料的各向异性。

1.2.3 压力声场建模

对于计算牵引变压器的辐射噪声,利用声-结构耦合的方式,将结构力场中的振动加速度作为激励,计算空气域中的压力变化。式(6)给出了声-结构耦合的控制方程。

(6)

式中:n为结构表面的法向;ρ为空气密度;Pt为总声压;qd为偶极子声源;ac为结构的振动加速度;FA为施加于结构上的载荷。

由于声压的变化对于牵引变压器结构振动的影响较小,将空气与变压器的接触面设置成单向耦合。在理想情况下,空气域应无限延伸,以此来避免空气域的边界发生声波的反射,影响计算的结果,为此利用式(7)调整了空气域的边界条件,使得出射波能够以最小的反射离开建模区域。

(7)

式中:κ(r)为波形函数;pi为入射压力场。

为有效计算声波在空气域中的传播,空气域的网格尺寸需要提供足够的波分辨率,所以利用式(8)限制了空气域网格的最大尺寸Lmax

(8)

式中,λmin为介质中声音的最小波长。

因为牵引变压器声辐射是由铁心与夹件的振动引起的,对于模型中空气与牵引变压器的接触边界,网格划分进行了加密处理。

1.3 模型验证

通过1.2节,建立了牵引变压器电磁场-结构力场-压力声场耦合模型,为了验证该模型的准确性,以1.1节中被测牵引变压器为研究对象,对比实测值与仿真值,模型的关键参数如表1所示,且模型整体被空气包裹。

表1 模型关键参数Tab.1 Key parameters of the model

模型仿真选择时域的计算方法,对于仿真步长,由图3可知,牵引变压器本体辐射噪声的显著频段为中心频率在100～1 000 Hz的三分之一倍频程频带内,噪声峰值主要出现在1 000 Hz以内100 Hz的倍频处,因此选择对比20～1 000 Hz内的仿真值与实测值进行模型验证。这需要对仿真模型计算的时域结果进行快速傅里叶变换(fast Fourier transform,FFT),得到其频域数据。对于采样频率为fs的信号,其在进行FFT变换后,分析频率范围为0～fs/2 Hz。基于此,仿真模型计算步长选为1×10-4s,这时采样频率fs为1×104Hz,那么分析频率范围为0～5 000 Hz,涵盖了进行模型验证所需的分析频率(20～1 000 Hz)。

模型仿真计算时长t选为0.2 s,这是因为计算时长t=0.2 s时,对仿真结果进行FFT变换后,其频率间隔f=1/t=5 Hz,由图3可知,牵引变压器辐射噪声峰值主要出现在100 Hz的倍频处,为5 Hz的倍数,并且为了减少模型计算所消耗的时间,综合考虑下选择计算时长t为0.2 s。

图6给出了仿真模型距离铁心顶端1 m处的声压经频谱分析后的结果,并与牵引变压器的实测值进行了对比,图6中实线为实测值,虚线为仿真值。

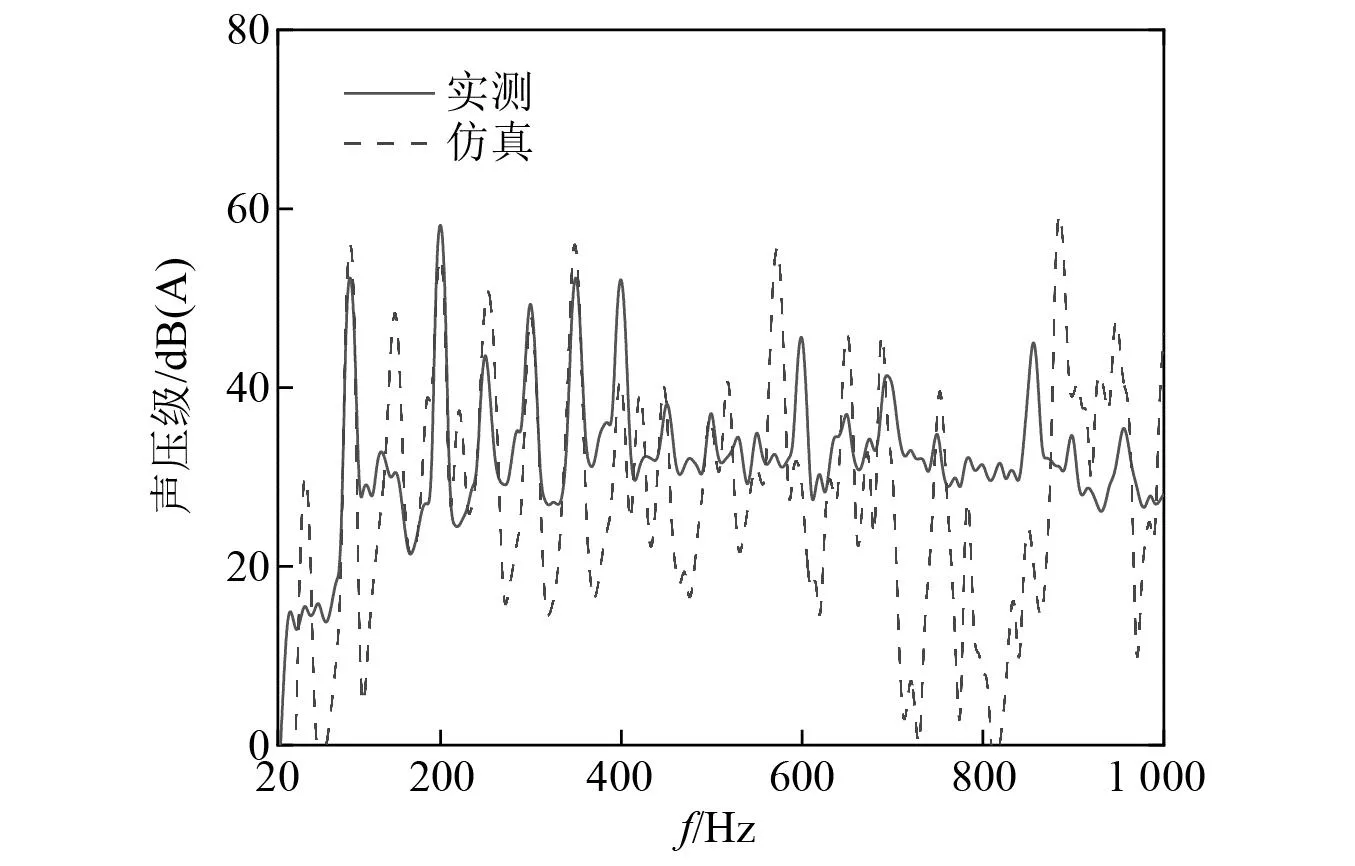
图6 仿真值与实测值频谱对比Fig.6 Spectrum comparison between simulated and measured values

由图6可知,牵引变压器辐射噪声的最大峰值出现在100 Hz处,为57.8 dB(A),在200 Hz与300 Hz处的峰值分别有56.3 dB(A)与49.9 dB(A),具有明显的谐波特征。

表2给出了仿真值与实测值的总值以及二者在100 Hz,200 Hz,300 Hz与350 Hz处的数据对比,噪声总值的计算频率范围为20～1 000 Hz。

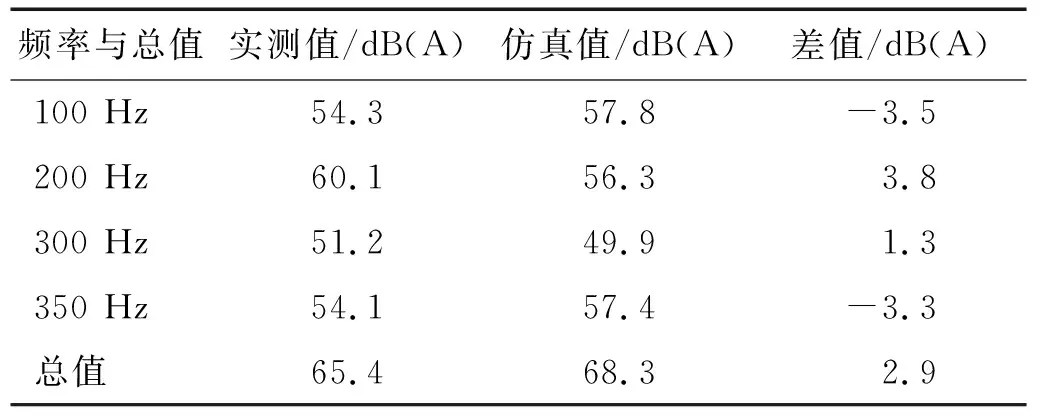
表2 仿真值与实测值对比表Tab.2 Simulation value and measured value comparison table

由表2可知,实测数据的总值为65.4 dB(A),仿真数据的总值为68.3 dB(A),二者差距2.9 dB(A)。仿真值与实测值在300 Hz处差值最小,为1.3 dB(A),在200 Hz处差值最大,为3.8 dB(A)。由图6可见,在700～1 000 Hz的频率范围内,仿真与实测相差较大,可能的原因是该模型的输入电压为正弦波,而牵引变压器在实际工作时,输入电压并非标准正弦波,其中往往包含着部分高次谐波,这些高次谐波的存在会增大变压器的高频噪声。总体而言,该模型100 Hz及其高次谐波处能有效仿真牵引变压器的电磁噪声。

2 市域列车车内噪声预测模型

为了明确牵引变压器作为激励源对市域列车车内噪声的影响,基于统计能量分析法建立了车内噪声仿真模型。

2.1 统计能量分析法基本原理

统计能量分析法(statistical energy analysis,SEA)是一种解决复杂系统的动力响应及声振耦合的有效方法。它的核心是能量在系统之间的流动,这其中包括外界激励将能量传递至系统内部、能量在子系统之间传递的损耗和子系统自身的能量损耗。其功率流平衡方程可表示为

(9)

式中:Ei为第i个子系统贡献的能量;Pi,Pj为激励源对子系统的输入功率;Pid,Pjd为子系统的耗散功率;ηid为子系统结构内损耗因子;Pij,Pji为子系统间的能量流动;ηij为子系统i和j间的耦合损耗因子,其满足互易性原理。

2.2 车厢SEA建模

根据SEA理论对某型市域列车的M2车建立了车内噪声仿真模型,模型考虑了市域列车的车体结构特征,划分了车厢子系统。子系统的划分过程基本遵循以下原则:

(1)对于共振模态参数类似的结构或声腔,划分为一类子系统,例如侧墙、地板与顶板子系统,以及车内声腔与车外声腔子系统;

(2)综合考虑列车结构的实际尺寸与计算的精度要求,尽可能使得各个子系统具备高模态数。

市域列车车内噪声预测模型如图7所示。

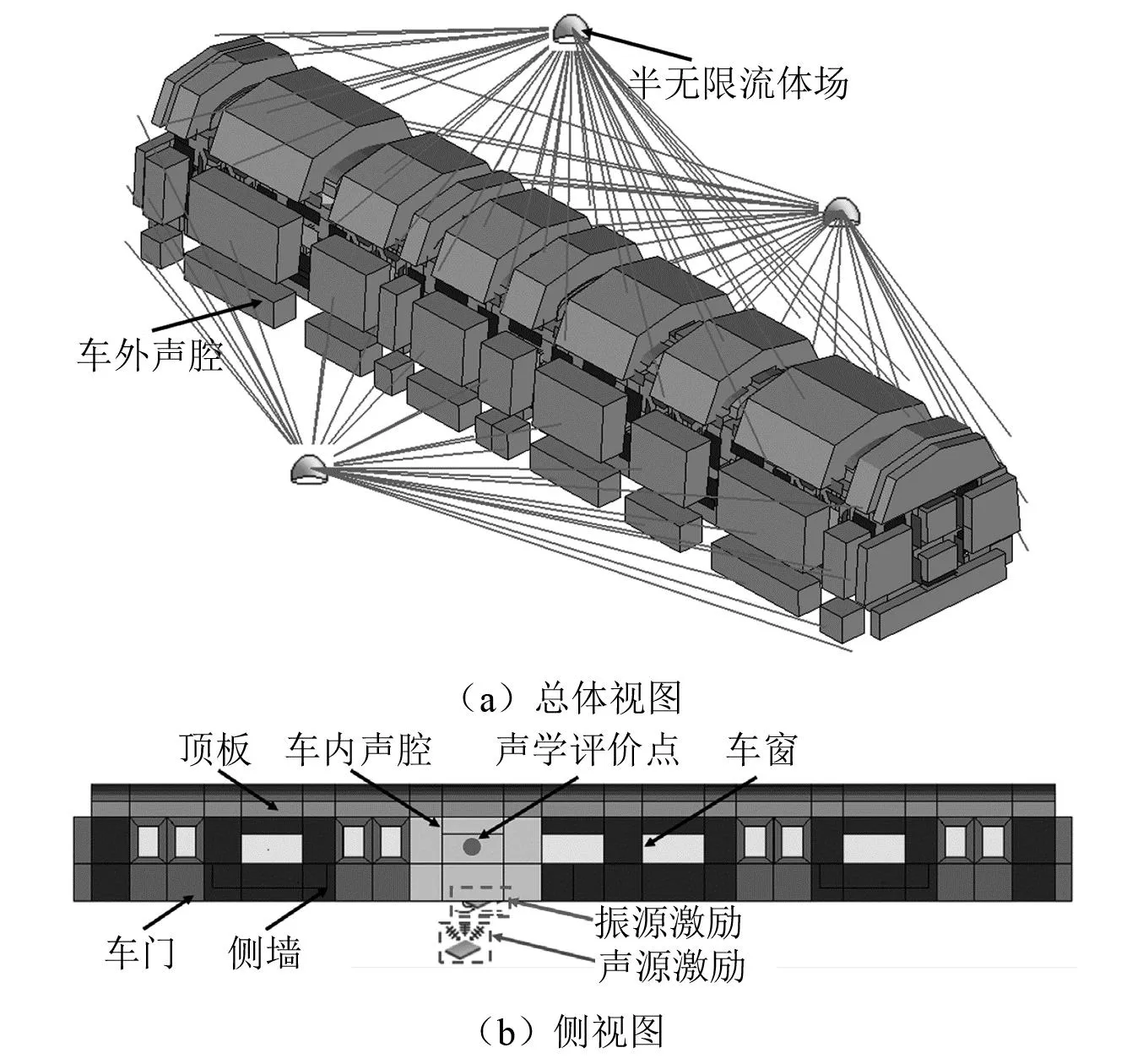
图7 车内噪声SEA模型示意图Fig.7 SEA model diagram of vehicle interior noise

市域列车车内噪声仿真模型的主要由声腔子系统、车体子系统与输入激励等组成。其中声腔子系统由车内声腔与车外声腔组成。由图7可知,车内声腔沿车身纵向方向划分为25组,沿车身高度方向划分为3组,沿车身横线方向划分为2组,车外声腔沿车辆纵向方向划分为12组,沿车身横向方向划分为3组。为了模拟列车两侧与顶部无反射的声学边界条件,在车外两侧与顶部声腔使用了半无限流体子系统进行声学连接。

车体子系统主要由平板与单曲面板组成,包括车窗、顶板、侧墙、地板与端墙等。在实际建模中,将车体的中空铝型材结构简化为铝合金板,忽略了车内尺寸较小的内饰结构。为考虑座椅的吸声对列车车内噪声的影响,按照车内座椅的实际尺寸与安装位置建立了简化的座椅子系统。由图7(b)可知,整个车厢的底部结构沿车身纵向方向划分了22组,沿车身横向方向划分了2组,侧面结构沿车身纵向方向划分了25组,沿车身高度划分了2组,顶部结构沿车身纵向方向划分了19组,沿车身横向方向划分了2～3组。

输入激励分为牵引变压器辐射噪声激励与振动激励。由图7(b)可知,噪声激励加载于车下空腔,振动激励加载于车体地板,且声/振激励的加载位置与该型市域列车牵引变压器的实际安装位置一致。通过建立各子系统之间的连接,噪声激励不仅会通过车体地板隔声传递至车内空腔,也会经由车体外部空腔,通过侧墙隔声影响车内噪声,对于振动激励,经由地板子系统与车内声腔子系统之间的连接,其也会对车内噪声产生影响。

2.3 SEA模型验证

将车内噪声模型的预测结果与市域列车静置状态且牵引变压器开启状态下的实测数据进行对比,结果如图8所示。

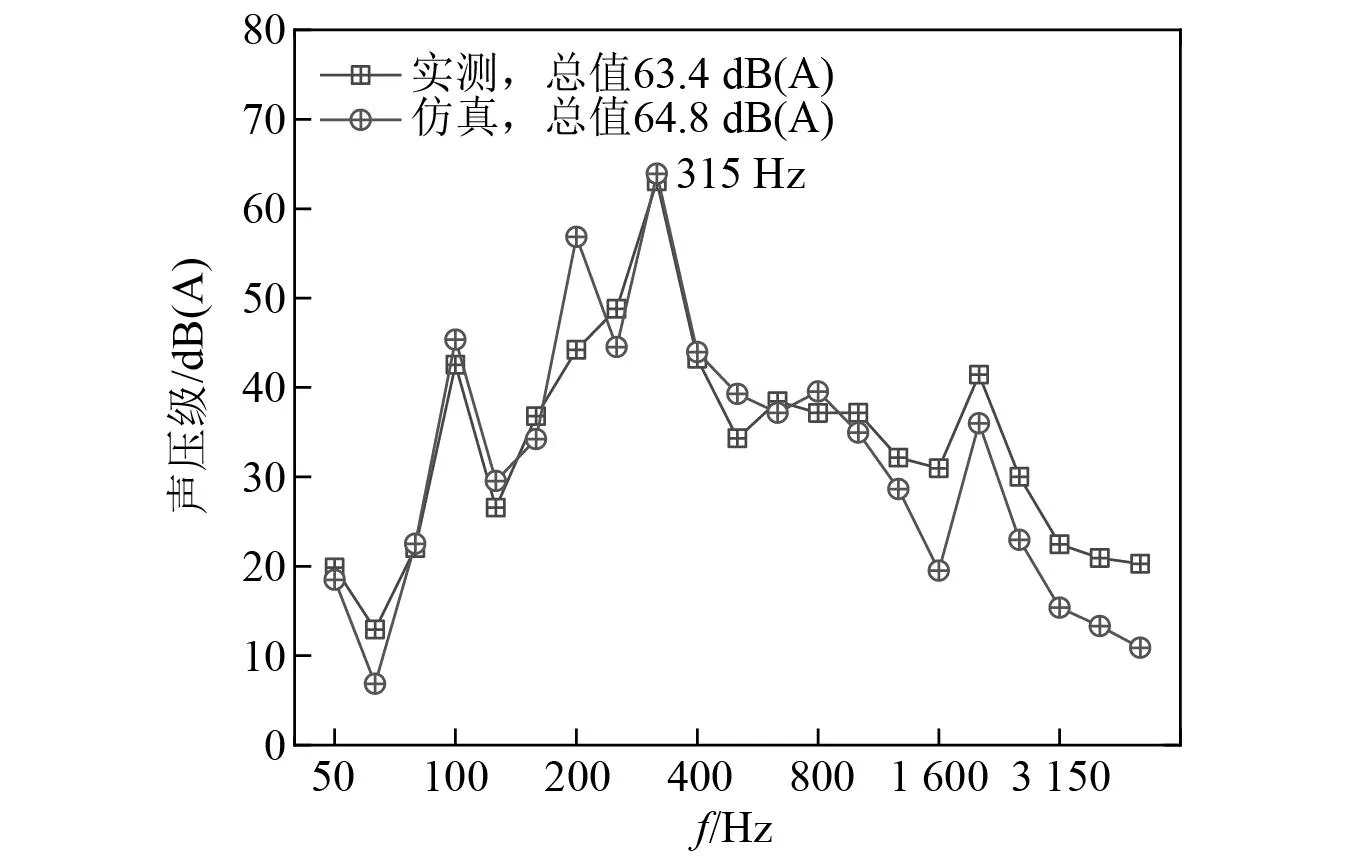
图8 仿真值与实测值对比Fig.8 Comparison between simulated and measured values

由图8可知,对于车内噪声总值,仿真与实测的差值为1.4 dB(A);实测与仿真数据的噪声显著频段分别为250～400 Hz与200～400 Hz,两组数据的噪声显著频段基本一致,但在200 Hz处仿真值与实测值差距较大,在峰值频率315 Hz处,市域列车车内噪声实测值与仿真值仅相差0.9 dB(A),可见该仿真模型在峰值处可以有效预测车内噪声;在50～1 000 Hz内,实测值与仿真值走势较为一致,声压级幅值拟合较好。综上所述,该模型能较好地预测车内噪声。

对于200 Hz处仿真值与实测值差距较大的问题,牵引变压器对市域列车车内噪声影响示意图,如图9所示。如图9所示,牵引变压器通常悬挂安装在市域列车的车体底架上,其本体的辐射噪声会经由车体缝隙的泄漏声或车体板件的隔声传递至车内,本体振动会通过悬吊元件传递至车内。由此可见,牵引变压器的振动噪声会通过多种方式影响市域列车的车内噪声,由于不同的传递方式会影响到振动噪声的频域特征,例如板件隔声对不同频率噪声的隔声效率并不相同,因此,牵引变压器本体辐射噪声与列车车内噪声的频谱特征会有所差别,这解释了为何图3表明牵引变压器本体噪声的峰值为200 Hz,而图8表明列车车内噪声峰值为315 Hz。

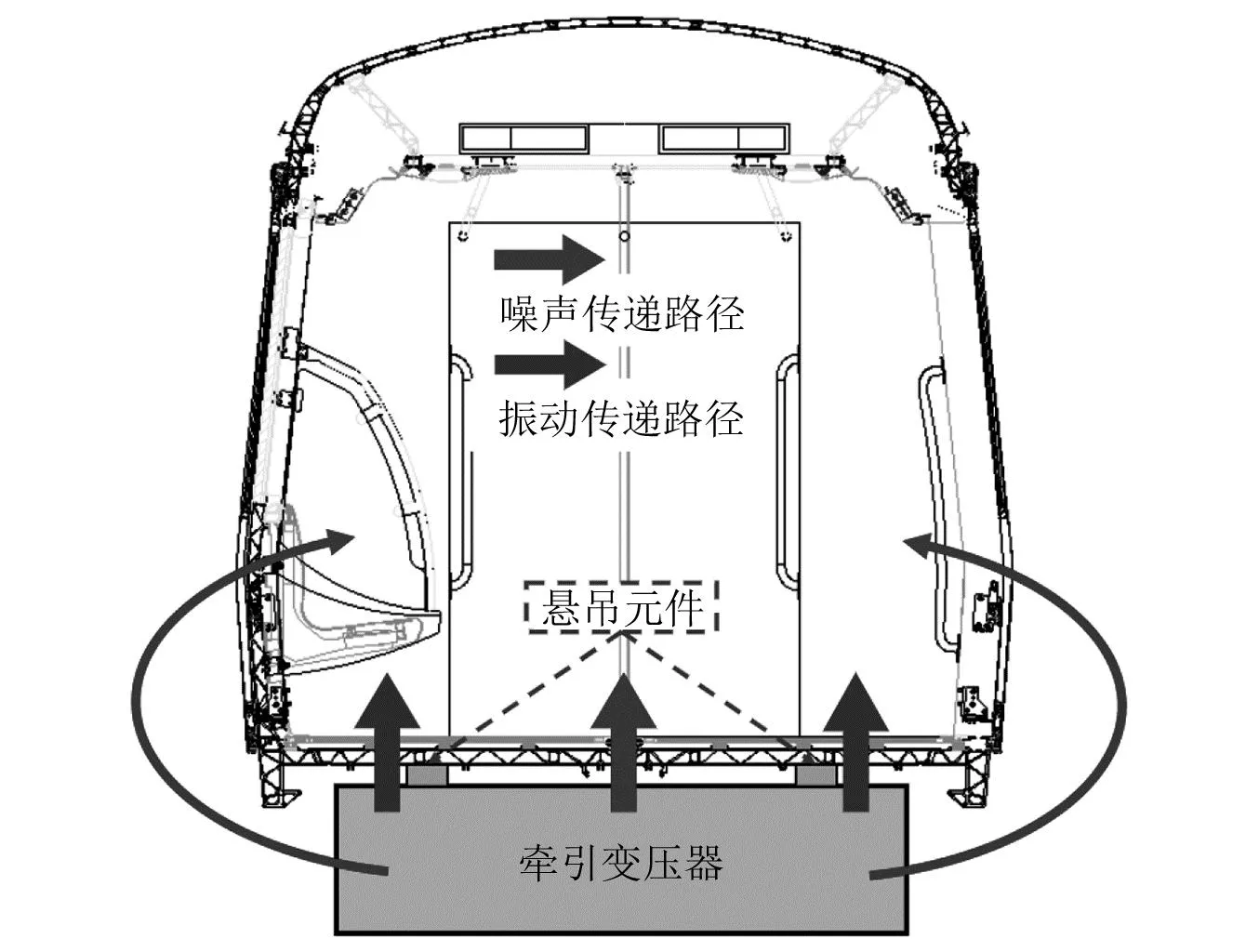
图9 牵引变压器对列车车内噪声影响示意图Fig.9 The influence diagram of traction transformer on train interior noise

3 牵引变压器降噪方案

3.1 降噪方案

为了降低牵引变压器的电磁噪声,在其箱体上贴附吸声隔声材料或增加减振装置是常见的降噪措施,但该措施更适用于宽频噪声,变压器噪声单频峰值占主要贡献,附加降噪材料的降噪效果有所降低,而且附加材料会增加变压器的质量,不利于市域列车的轻量化设计。因此,需要采用其他方式实现牵引变压器降噪。

对于空载运行的牵引变压器,其辐射噪声能量的主要来源为铁心,因此牵引变压器降噪的关键在于降低铁心振动,具体考虑结构与电磁两方面。结构方面是通过抑制铁心及其各部件的振动实现牵引变压器降噪,电磁方面主要是考虑降低铁心内部的磁通密度。为提升结构刚度,常用措施为更换材料,如部分硅钢片的刚度值可达300 GPa,此外还可以通过结构表面喷涂聚酯胶与优化结构等方式增加刚度,为降低磁通密度,通过优化线圈结构与分布为常用措施[20-21]。在本文模型的基础上,给出了4种降噪方案,如表3所示。

表3 牵引变压器降噪方案Tab.3 Traction transformer noise reduction scheme

为合理制定各方案优化后的参数值,需要进行牵引变压器辐射噪声影响参数调查,以夹件垂向刚度优化过程为例,将该参数分别提高20%,40%,60%,80%,100%与120%,计算不同参数下的辐射噪声总值。不同夹件垂向刚度时的计算结果,如图10所示。

图10 优化夹件垂向刚度计算结果Fig.10 Optimization of vertical clamp stiffness calculation results

由图10可知,牵引变压器辐射噪声总值随着刚度的增加呈现先减小后增大的趋势,出现这一趋势可能的原因是夹件垂向刚度的增加改变了牵引变压器整体结构的固有频率,增大了结构共振引起的振动响应。因此,将刚度增大80%作为垂向夹件刚度的优化方案。

3.2 降噪方案分析

为了分析各个牵引变压器降噪措施对市域列车车内噪声的影响,提取了不同降噪方案下牵引变压器仿真模型中的声振激励,将其加载至车内噪声仿真模型,计算车内噪声,并将该结果与仿真激励下的车内噪声进行对比。采取降噪措施前后市域列车车内噪声的仿真结果,如图11所示。图11中虚线为采取降噪措施前的仿真值,实线为采取降噪措施后的仿真值,图11中噪声总值的计算频率为50～5 000 Hz。

图11 牵引变压器降噪方案对比Fig.11 Comparison of Noise Reduction Schemes for Traction Transformer

由图11可知,对于增加夹件垂向刚度的方案一,对比原方案,车内噪声总值降低了2.4 dB(A),原方案与方案一的噪声显著频段均为250～400 Hz,在315～600 Hz以及1 600～3 150 Hz范围内,方案一的噪声相比于原方案有所降低。对于增加夹件横向刚度的方案二,对比原方案,车内噪声总值降低了2.6 dB(A),噪声显著频段变为250～630 Hz,夹件横向刚度的增加有效抑制了315 Hz处的噪声峰值,但是增大了400～630 Hz范围内的噪声。对于增加铁心刚度的方案三,对比原方案,车内噪声总值降低了8.2 dB(A),噪声显著频段变为200～500 Hz,铁心刚度的增加有效抑制了100 Hz与315 Hz处的噪声峰值,并且对630～5 000 Hz范围内的噪声也有明显的抑制效果,这是由于铁心刚度的增加从源头上抑制了铁心的振动。对于降低铁心内磁通密度的方案四,对比原方案,车内噪声总值降低了4.4 dB(A),噪声显著频段不变,依旧为250～400 Hz,铁心刚度的增加有效抑制了315 Hz处的噪声峰值,并且对50～5 000 Hz范围内的噪声均有一定的抑制效果,但是在高频段这种抑制效果更明显,这是因为磁通密度的降低缓解了铁心的磁场饱和,减小了磁场饱和引起的磁通密度中的谐波分量,因此磁通密度的降低对高频段噪声的抑制效果更明显。

以上四种方案均可在一定程度上降低车内噪声总值,综合比较而言,从根源上降低铁心振动噪声的方案三与方案四,不仅可以有效降低车内噪声总值,而且对高频范围内噪声也有较强的抑制效果。在实际工程应用中,以上四种方案均可作为牵引变压器降噪措施,具体还需结合牵引变压器电磁噪声的频谱特征进行综合选择。

4 结 论

本文针对市域列车牵引变压器的声辐射特性进行了测试,建立了用于分析市域列车车内噪声受牵引变压器影响的单向耦合模型。结果表明:

(1)牵引变压器的辐射噪声在100 Hz及其倍频处存在显著峰值,具有明显谐波特征,且主要集中在1 000 Hz以内。牵引变压器声辐射仿真模型的仿真结果在中低频尤其是峰值处与实测值吻合较好,高频处的误差可能原因是输入电压为理想正弦波,与含有丰富高次谐波的实际电压不一致。

(2)建立了牵引变压器辐射噪声仿真模型与市域列车车内噪声仿真模型,分别将牵引变压器声振激励的实测值与仿真值加载至车内噪声仿真模型,对比了仿真结果与车内噪声的实测值,结果表明,将牵引变压器仿真模型的结果作为激励,可以较好地反映牵引变压器振动噪声对列车车内噪声的影响。

(3)根据牵引变压器电磁噪声产生机理与频谱分布特征,从结构与电磁两方面提出降噪措施,各措施对降低车内噪声均有一定的效果,其中增加铁心刚度与降低铁心磁通密度的措施效果最突出,在实际工程应用中可结合具体情况进行综合考虑。