单套索人工肌肉的力学特性建模及试验分析
杨明星, 夏玉磊, 刘庆运, 汤国庆, 郑近德
(1.安徽工业大学 特种重载机器人安徽省重点实验室,安徽 马鞍山 243032; 2.安徽工业大学 机械工程学院,安徽 马鞍山 243032)
套索传动装置主要由具有外部的螺旋中空套管、内部的柔性钢丝绳索、端部固定的螺栓以及其它紧固件组成,具有结构轻巧柔软、质量轻、传输路径灵活多变、输出力矩大的优点。此外,套索传动装置还能够穿过狭窄弯曲的空间进行远程动力传递,并巧妙地实现驱动部件和执行部件的分离,可以有效简化机械结构的本体设计,降低系统整体的质量和体积。目前,套索传动系统被广泛用于多种类型的机器人及其传动装置的系统设计中,如仿生灵感下的弹性执行器设计[1]、穿戴式外骨骼机器人的驱动部件外置[2]、机器人灵巧手的远端驱动控制[3]以及多功能连续体机器人的姿态操作[4]等。但由于套索驱动系统中存在绳索受力状态时的长度变化、套管和绳索间的摩擦等因素的影响,引入了死区、间隙和迟滞等诸多非线性特性,这不仅会造成套索系统在传动过程中的能量损耗,而且严重影响末端执行器的精确定位和可靠性操作[5-6]。
为了建立精确的数学模型,消除工程应用中因传?动死区、摩擦、迟滞等特征的影响,国内外许多学者对套索传动的非线性特性进行了研究,并取得了一些进展。意大利博洛尼亚大学的Palli等[7]使用类LuGre动态摩擦模型来研究绳索的蠕变现象,并基于静摩擦模型对具有前馈摩擦补偿的套索拉力控制展开了研究。为了描述套索驱动手术机器人中因摩擦效应引起的迟滞现象,新加坡南洋理工大学的Do等[8]提出一种改进的归一化Bouc-Wen模型来模拟绳索和套管之间的摩擦特性,并通过计仿真计算和试验验证了模型的正确性。加拿大瑞尔森大学的Norouzi-Ghazbi等[9]基于内部驱动机构和柔性体之间的连续交互作用,建立了等效的离散模型来模拟具有连续相互作用的套索传动柔顺特性,完成了驱动端到连续体机器人末端执行器之间力传递未知参数的识别。韩国科学技术高级学院的Rho等[10]利用电动机驱动套索方式进行了便携性柔性外骨骼手套的设计,提高了整个装置的功率/质量比,但是没有进行力-位移关系的建模分析。东南大学的王兴松教授课题组成员一直致力于套索传动技术相关的研究,团队在套索系统力矩传动特性分析与建模[11]、驱动执行器设计[12]及其在外骨骼机器人[13]中的应用等方面均有丰硕成果产出。
在套索传动路径上适当增加弹性元件可以减小执行器所受到的冲击,从而使机器人获得更好的柔顺交互性能。意大利理工学院的Di等[14]设计了一款以套索作为驱动方式的下肢外骨骼机器人,在套索输出端位置增加了弹簧并配备了弹簧预紧装置,保证了系统的柔顺性和控制精度。西安电子科技大学的李清桓等[15]设计了一款绳索驱动并联机器人,将弹性元件加入绳索传动中,起到增加张紧作用的同时改善了系统的刚度,但建立的传输模型对柔性绳索传动特性的解释不够充分。中科院沈阳自动化研究所的刘自文等[16]设计了一款套索传动的柔性外骨骼手套,进行了人体穿戴抓取物体的力控制试验。南京航空航天大学的陈柏等[17]提出一种基于套索的人工肌肉驱动器,该人工肌肉由套索、拉伸弹簧和压缩弹簧构成,三者共同作用可实现相当的弹性和柔顺性。上述研究工作主要集中于套索传动在应用中的功能实现,对于在新型驱动装置中出现的特有死区、摩擦、迟滞等现象缺乏针对性的理论分析,在一定程度上制约了新型执行器性能的进一步提升。
本文将Hill肌肉模型与套索传动机构相结合,提出了一种新型的单套索人工肌肉驱动器,该装置具有简单的机械结构和优异的柔顺驱动性能,为创新性柔顺驱动器的实现提供了一种思路。分别从静力学和动力学的角度对套索传动机构进行了建模和分析,根据刚度关系将输入位移选为动力学模型输入,提高了模型的实用性。在此基础上分析了套索人工肌肉传递特性影响因素,并搭建试验台进行了试验验证,所得结论为套索人工肌肉的工程应用提供重要的理论支持。
1 单套索人工肌肉传动特性建模
如图1(a)所示,单套索人工肌肉的设计灵感来自Hill肌肉模型。Hill肌肉模型是描述肌肉特性的一种简单而有效的方式,在简化肌肉的功能和结构之后,它主要包括三种物理元素:一个可控收缩力的收缩元CE、一个与CE并联的弹性元PE、一个与CE和PE串联的弹性元SE[18]。其中,CE产生的力等于SE产生的力,最终肌肉模型产生的力等于PE和CE的组合,这三个要素协同作用,以顺利实现特定肌肉的传输特性。

图1 基于Hill模型的单套索人工肌肉原理示意图Fig.1 Schematic diagram of a single tendon-sheath artificial muscle based on Hill model
结合Hill三元素模型以及套索传动系统,得到如图1(b)所示的单套索人工肌肉整体结构方案。其中,传动系统的末端连接到一个拉簧,该拉伸弹簧在系统中充当负载。电机驱动的套索部分作为肌肉的主动收缩元CE为系统提供收缩力和位移,套管末端与挡块之间的拉伸弹簧可以看作为人工肌肉的串联弹性元SE,绳索与挡块固连后与负载拉簧相连。并联弹性元PE的一端固定,另一端通过挡块与绳索单向连接。当肌肉长度小于原长度时,挡块与PE之间无接触,PE弹性元不参与作用;当肌肉被拉伸超出原长时,挡块会带动PE向外拉伸,此时PE就会承受部分拉力。PE在被拉到一定程度时可承受绝大部分负载以保护系统的结构。本文设计的单套索人工肌肉结构轻巧、输出力大,具有类似肌肉的弹性及收缩机制。为了研究套索人工肌肉的传动特性并进一步提高其在致动器中的应用性能,有必要对其传动性能相关的静力学特性和动力传动特性进行分析。
1.1 单套索人工肌肉静力学建模
(1)单套索传动静力学建模
如图2所示为单套索传动模型,通常情况下套索在工作时可以看作是一条任意光滑的空间曲线。套管的两端分别固定在J,K两处,Xin,Fin分别表示传动系统的输入位移与输入拉力,Xout,Fout分别为系统相应的输出位移与输出拉力,x是指从J点起沿套管方向的弧长,L为套管的总长度,kL为弹性负载的刚度。
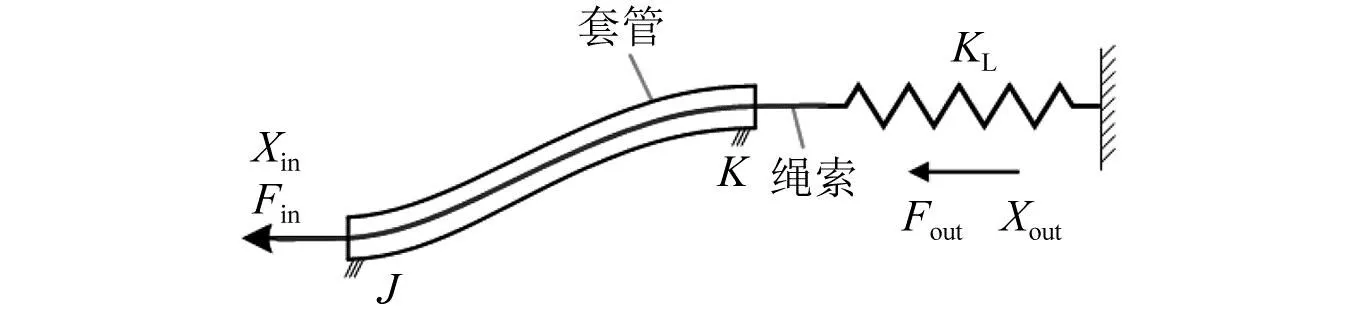
图2 任意形状的单套索传动模型Fig.2 A single tendon-sheath transmission model with arbitrary shape
考虑到套索的摩擦力主要由弯曲绳索所受的轴向拉力产生,为了进一步定量分析套索力与位移之间的传递关系,可以通过微元分析方法建立空间任意曲线形式的套索传动模型。如图3所示,可将套索分割成若干段,每一段可作为一个二维微元体,取弧长x处的微元体进行分析,R(x)为微元弯曲半径,F(x)与F(x+Δx)分别为目标套索微元两端的拉力,Δx代表微元弧长,Δθ是微元弧长所对应的圆心角,Ff与FN分别为套管对绳索的动摩擦力和法向压力。

图3 套索的微元体受力分析Fig.3 Force analysis of the tendon-sheath element
对套索微元进行受力平衡分析可得
(1)
(2)
考虑当微元足够小时,高阶无穷小量dF(x)sin(Δθ/2)可以忽略不计,cos(Δθ/2) =1且sin(Δθ/2)=Δθ/2。因此式(2)可写为
(3)
因为,消去式(3)中的Ff和FN可得
(4)
式中,κ(x)为弧长x处套管的曲率。

(5)
式中:ξ(L)为整条套索曲线的弯曲程度;F(0),F(L)分别为输入端和输出端的拉力。
由于系统中的绳索存在弹性形变,当输入拉力方向刚开始改变时输出端的拉力仍保持上一时刻的值而不会立刻响应,直到输入端拉力减小至输出端拉力足以反向拉动整段套索为止。其数学表述为
(6)
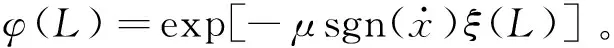
假设绳索一直处于弹性形变范围内,根据胡克定律可以获得套索微元的形变量为
(7)
式中:dδ(x)为x处微元体的形变量;E,A分别为绳索的弹性模量和横截面积。
假设绳索不存在轴向转动,可在区间[0,L]内对式(7)进行积分描述套索传递路径上总的变形量为
(8)
套索变形量与力的传递有相似之处,假设在t0时刻输入端运动方向改变时其输出端位移保持不变,直到进入下一个响应阶段。因此,套索总形变量表述为
(9)
此时,套索输入位移和输出位移的关系为
Xout=Xin-δ(x)
(10)
因此,单套索传动机构中静力学研究的力与位移传递关系可通过式(5)、式(9)以及式(10)来描述。
(2)单套索传动死区分析
由于套索传动死区对本研究套索人工肌肉的传动特性有一定影响,有必要针对影响套索死区大小的因素进行分析。
在套索由拉伸状态转变为放松状态时会经过一个放松死区,由放松状态变为拉伸状态时会经过一个拉伸死区。放松位移死区为拉伸状态结束时拉索的总伸长量与放松状态下输出端将有位移输出时拉索的总伸长量之差,这两个状态点的输入拉力之差即为放松力死区。具体推导过程如下。
为了简化结论推导,这里不妨假设套管曲率半径为定值R。令P,P′分别为放松位移死区和放松力死区的输入位移变化量,根据式(6)和式(9)可得
(11)
P′=Fin1-Fin2
(12)
式中:ε1=1-exp(-μξ(L));ε2=1-exp(μξ(L));Fin1为放松死区起点时套索输入端拉力,Fin2为放松死区终点套索输入端拉力。令F01为放松死区套索输出端拉力,由式(6)可知Fin1与Fin2可表示为
(13)
联立式(11)~式(13)可得
(14)
由式(14)可以看出当套索全曲率ξ(L)不变时,随着R值的增大,套索传动位移的损耗和位移死区也将增大。值得注意的是,相同情况下拉力死区不受套管半径R的影响。
为了探究摩擦因数μ以及全曲率ξ(L)对放松死区的影响,根据式(14)将放松位移死区函数P分别对全曲率ξ(L)、摩擦因数μ进行求导可得
(15)
式中,ζ=μξ(L)(eμξ(L)-e-μξ(L))-eμξ(L)-e-μξ(L)+2。
已知式(15)中的参数均为正数,显然放松位移死区P及其对ξ(L)的导数值恒大于零,故随着全曲率ξ(L)的增大,放松位移死区P也会随之增大。此外,由式(15)无法直接看出ς与0的大小关系,可将ς视为μ的函数,ς(μ)的导数为
(16)
式中,参数均为正数,所以ς(μ)的导数大于零,并且由ς(0)=0和μ>0可知ς(μ)>0,从而可得P对μ的导数值大于零。因此,随着摩擦因数的增大,拉伸位移死区也会随之增大。同理可证放松力死区P′随着摩擦因数μ的增大而增大,放松力死区P′也随着全曲率ξ(L)的增大而增大。拉伸死区分析情况与放松死区的分析方法相同,在此不再赘述。
综上,全曲率ξ(L)、摩擦力μ的增大将会增加套索在传动过程中力和位移的损耗。除此之外,全曲率一定时,位移死区还随着套管半径R增大而增大,但拉力死区不受套管半径R的影响。
(3)单套索人工肌肉建模
为便于分析,本研究基于Hill肌肉模型的套索人工肌肉的结构原理如图4所示。首先假设在t1时刻挡块开始与并联弹性元PE相互接触,设此时人工肌肉长度变化量ΔLe以及套索输出位移Xout均为0。

图4 Hill人工肌肉结构原理图Fig.4 Structural schematic diagram of the Hill artificial muscle
人工肌肉的长度等于原长的初始时刻,因并联弹性元PE承载的拉力小于其初始内应力Fj,其长度并无明显变化,当其内应力被完全克服后会促使并联弹性元开始动作。因此,给定Xj=-Fj/kSE和Xc=Xout(t)-Xout(t1),则有
(17)

此时,对挡块节点处受力分析,可得
Fm=FPE+FSE
(18)
式中,FSE=FCE=F(L,t)。
将式(6)、式(17)和式(18)联立求解,可得人工肌肉力传递特性表达式为
(19)
由式(19)可以看出:当人工肌肉长度小于原长时并联弹性元不参与作用,此刻Xout≥0,λ=FPE=0,Fm=FCE;在t1时刻,并联弹性元与挡块开始相互接触,此时FPE=0且Fm=FCE;当PE承载部分力但其长度几乎不发生改变(即0>Xc>Xj)时,FPE=|Xc|kSE,肌肉输出力由PE和SE共同提供;当肌肉长度变化量为ΔLe>0时,PE承担的拉力与长度变化量遵循胡克定律。基于上述分析,选取合适参数对套索人工肌肉静态模型进行仿真,所得拉力及位移传递特性曲线如图5所示。
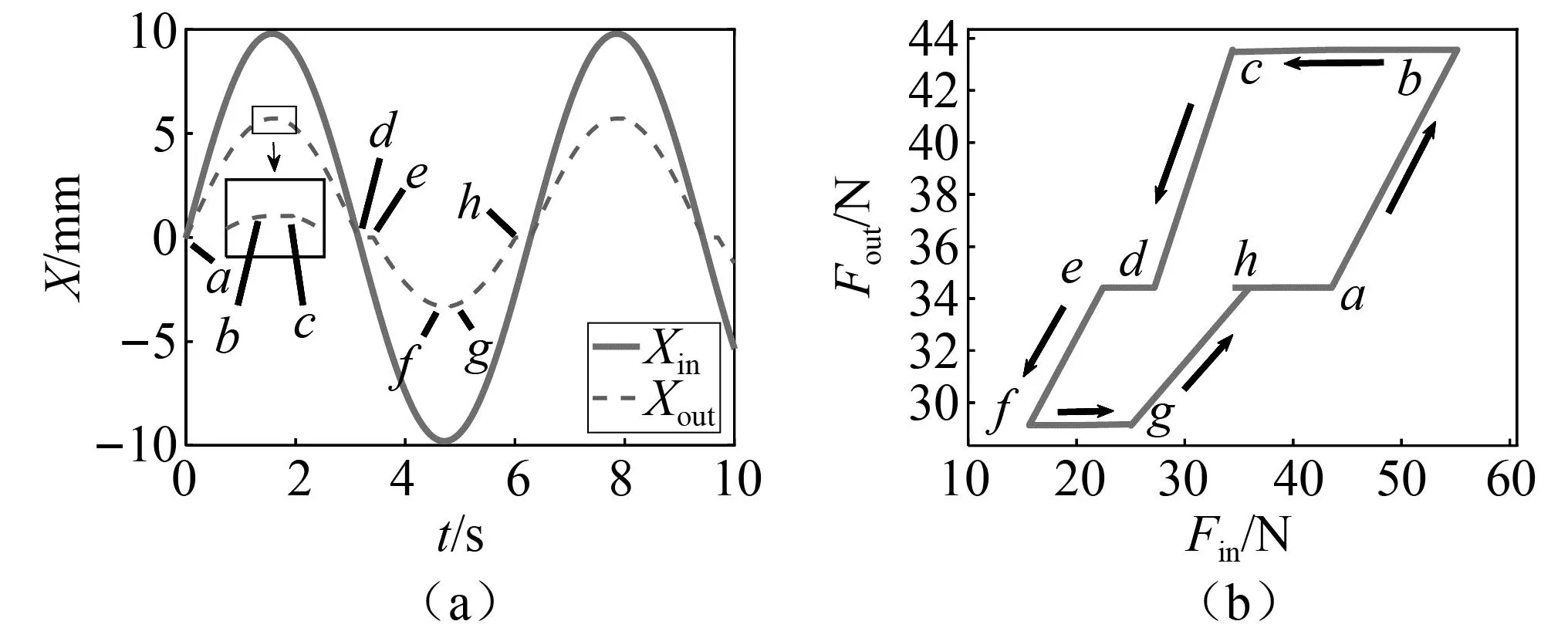
图5 套索人工肌肉的静态模型仿真Fig.5 Static model simulation of the tendon-sheath artificial muscle
a~b过程,电机输入位移从0增至9.8 mm,系统输出拉力从34.4 N增至43.6 N;b~c过程,电机反转,电机输入位移由9.8 mm减至9.7 mm,因死区的存在,其输出端无响应,输出拉力保持在43.6 N附近;c~d过程,电机输入位移继续减至0,输出端拉力逐渐从43.6 N减至34.4 N,因挡块只在人工肌肉伸长时起作用,此时并联弹性元不参与作用;d~e过程,电机输入位移由0减小至-2.82 mm,并联弹性元受到的拉力小于其内应力,其长度无明显变化,人工肌肉输出力保持在34.4 N附近。至此完成了人工肌肉的半个动作周期,后半个周期与前半个周期类似,在此不再赘述。
1.2 单套索人工肌肉的动力学建模
在上述静力学模型中忽略了绳索的质量以及速度对力的影响,因此在动力学模型中加入了绳索质量和阻尼。如图6所示,将图2所示的绳索分成n个首尾相连的弹簧-质量-阻尼系统,其中xin,xout,Fin,Fout和kL分别表示系统输入位移、输出位移、输入拉力、输出拉力以及负载的弹性系数;xi,mi,ki,fi,ci分别表示第i个套索单元的位移、质量、弹性系数、来自套管的摩擦力和阻尼系数。
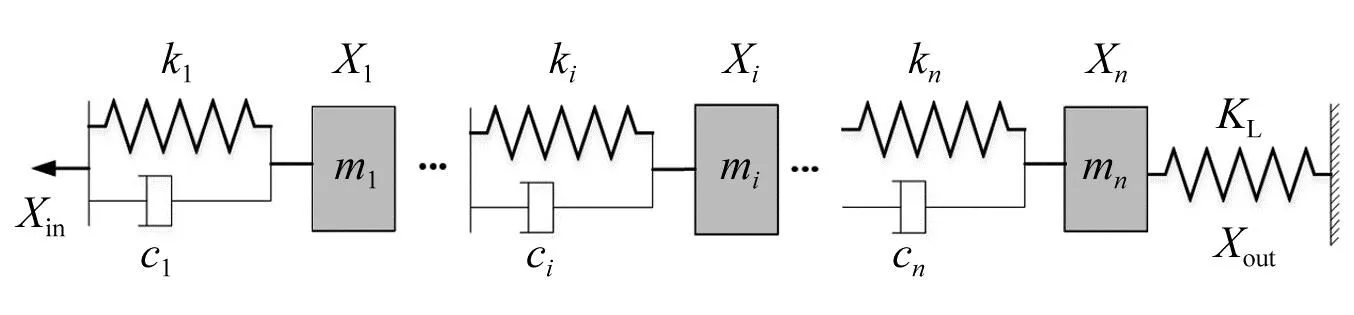
图6 单套索传动的动力学模型示意图Fig.6 Schematic diagram of dynamic model for the single tendon-sheath transmission
根据牛顿方程,对第i个弹簧-质量-阻尼系统受力分析可得
(20)
式中:1≤i≤n;x0=xin;cn+1=0。此时,输出力和位移可表示为
(21)
式中,F0为预紧力。
如图7所示,在动力学的基础上加入串联/并联弹性元后,套索人工肌肉的运动过程可以分为如下三个阶段。
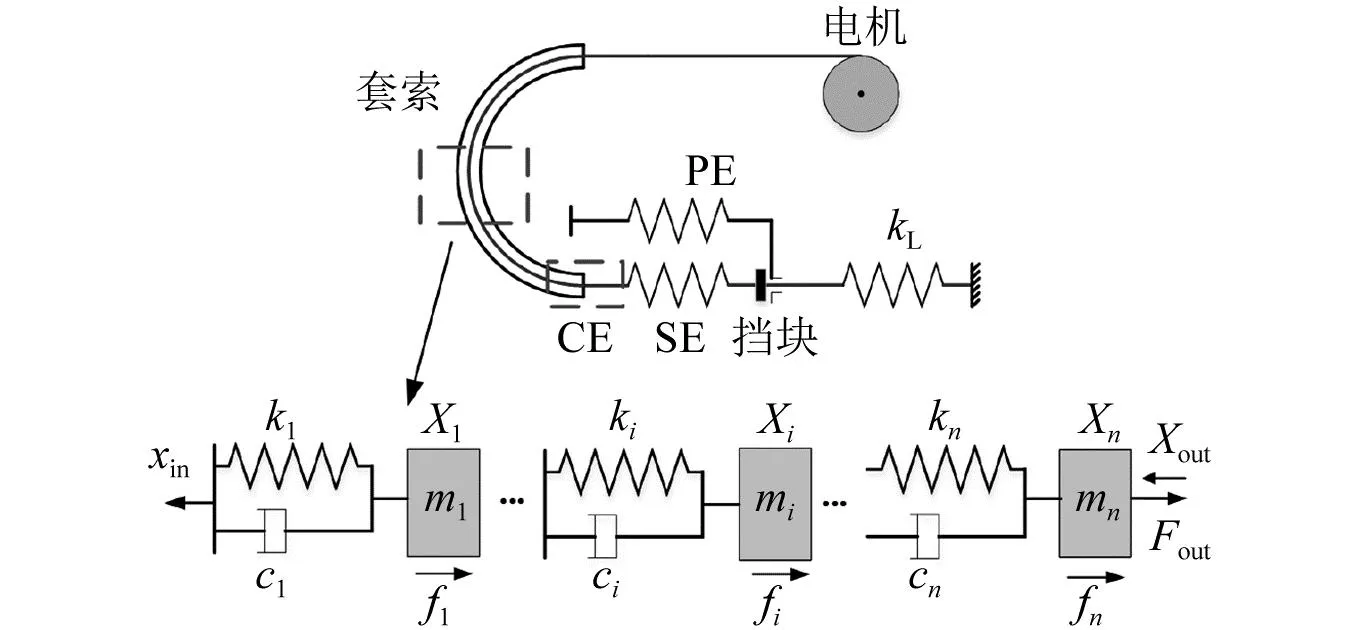
图7 套索人工肌肉的动力学模型图Fig.7 Dynamic model diagram of the tendon-sheath artificial muscle
第一阶段:舒张阶段。此时并联弹性元参与作用,人工肌肉的长度大于原长,此时动力学方程表述为
(22)
式中:Kr1=kSE(kPE+kL)/(kSE+kPE+kL);0≤xn≤A-xj;A为输入位移的幅值;xj=Fj/kSE;Fj为并联弹性元作用时的内应力。
第二阶段:克服弹簧内应力阶段。由于并联弹性元存在初始内应力,使得当并联弹性元达到原长时其上依然存在力,此时串联弹性元需要继续拉伸至其上的拉力与负载弹簧拉力相等时,并联弹性元拉力为零,此时动力学方程表述为
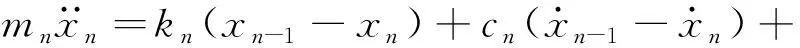
(23)
其中,
第三阶段:收缩阶段。此时并联弹性元不参与作用,人工肌肉可简化为串联弹性元与负载弹簧串联的模型,其动力学方程可表述为
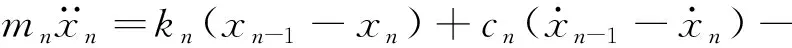
(24)
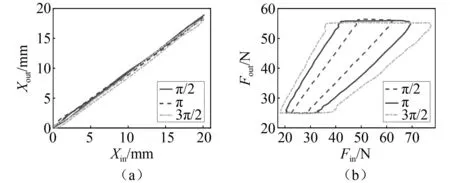
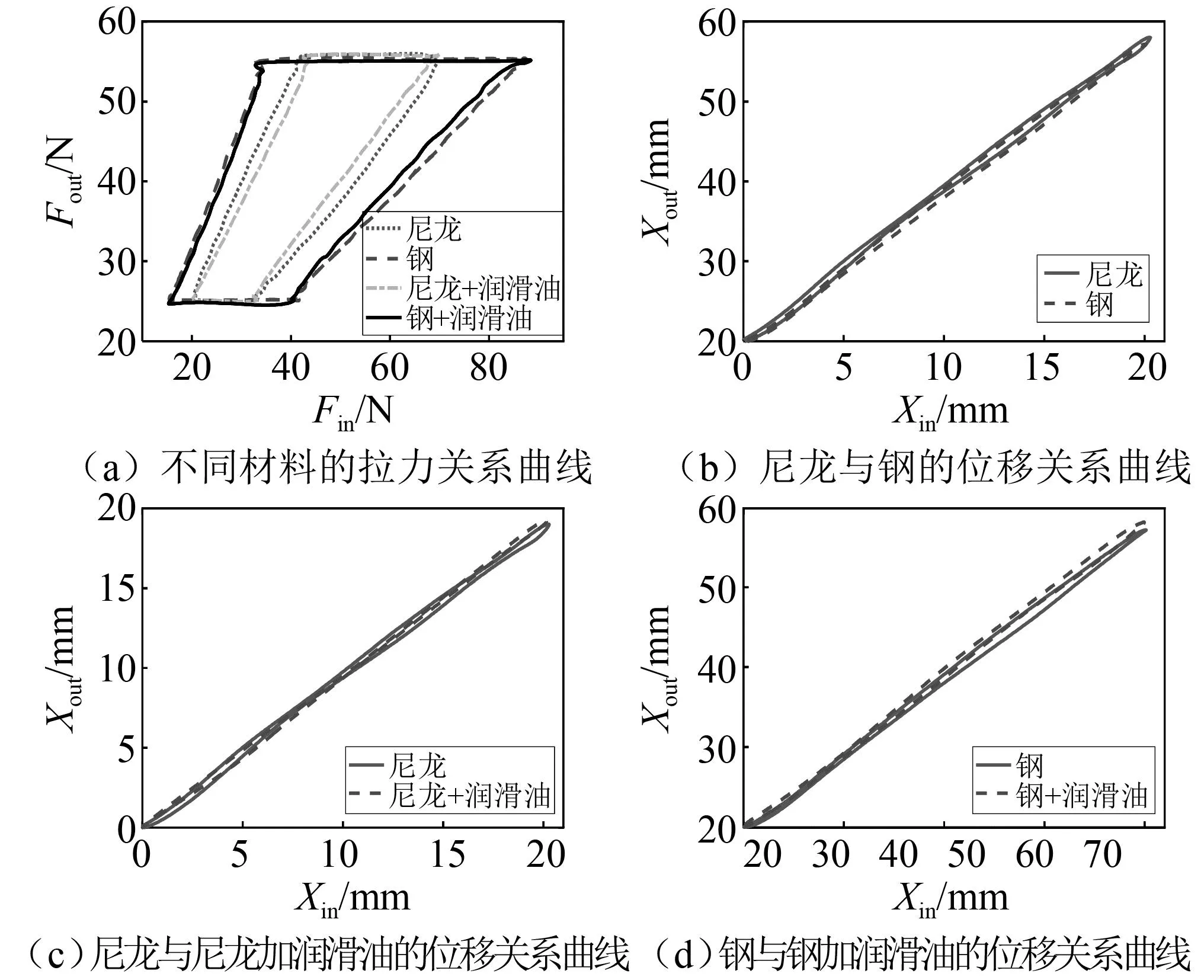
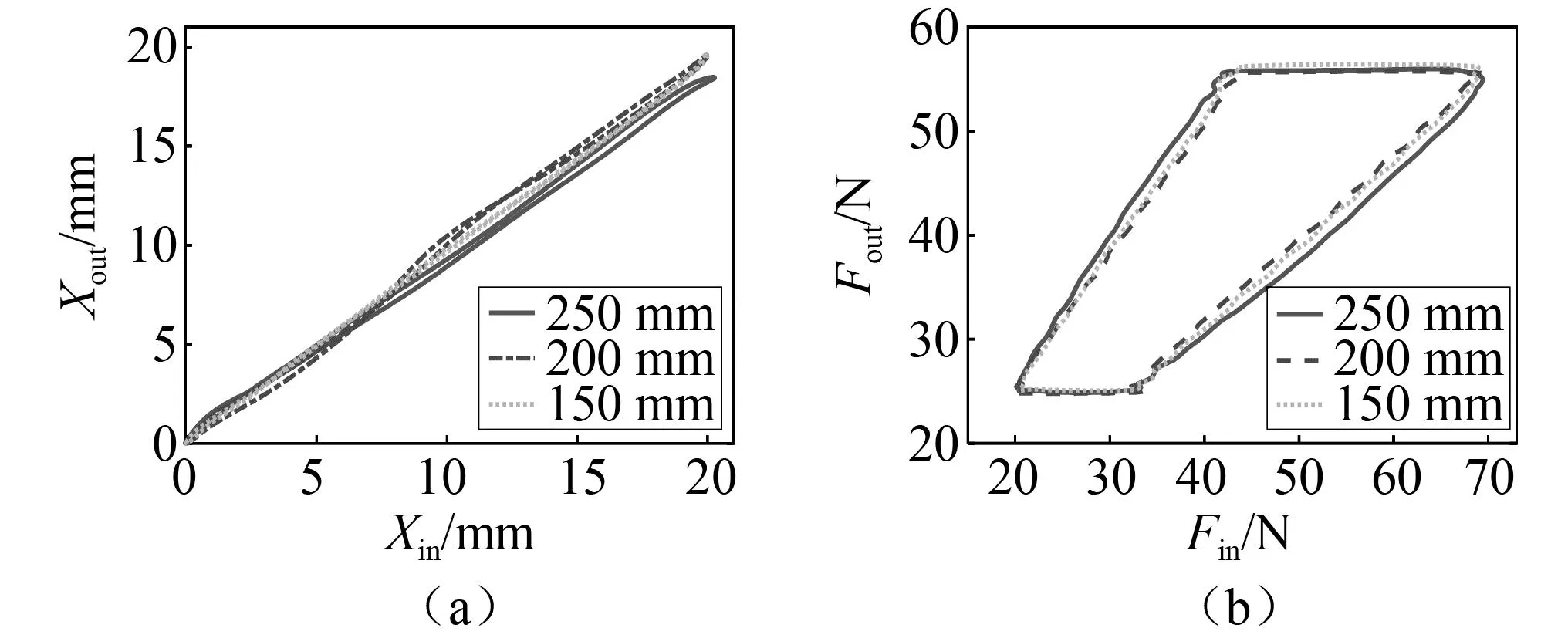
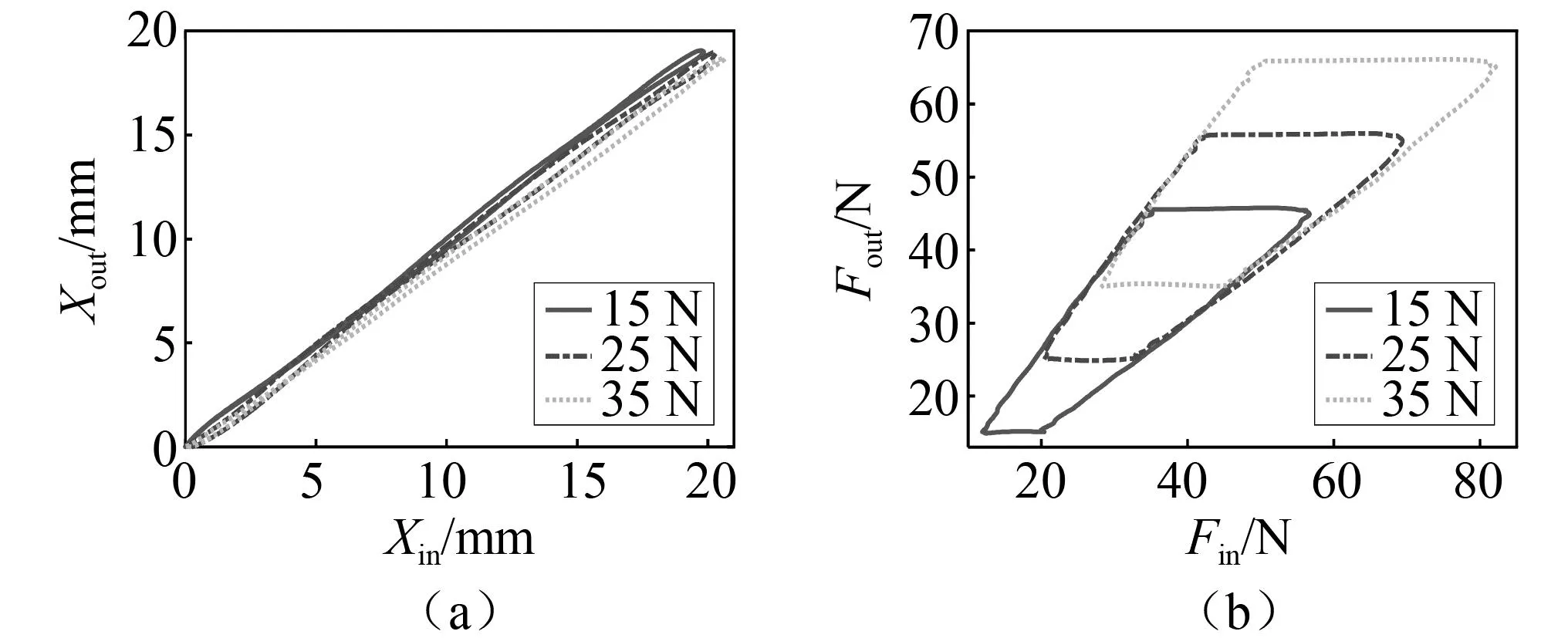
式中,A 针对套索传动系统力传递死区明显的问题,为了提高模型的实用性,将系统输入端位移选为动力学模型的输入。综上所述,可得套索传动的动态模型为 (25) 其中, (26) (27) (28) M,K,C均为n阶方阵,M可描述为 M=diag(m,…,m) (29) K可描述为 K=K(i,j) (30) 式中,1≤i≤n,1≤j≤n,K(n,n)=km。当i=j C=C(i,j) (31) 式中,1≤i≤n,1≤j≤n,C(n,n)=-c。当i=j 综上所述,式(25)中除了未知的摩擦力向量fn×1,其余参数均为已知或可求量。因此,对套索动力学模型求解问题转换成了处理套索内部摩擦力的问题。考虑LuGre动态摩擦模型可以准确地描述库伦摩擦、黏性摩擦、预滑动、Stribeck效应等现象,同时又具有良好的实用性、求解方便容易理解等优点。本研究采用Lugre模型对系统的摩擦进行描述,Lugre模型的数学描述为 (32) 式中:z为刚毛平均变形量;x为两接触表面相对位移;f为摩擦力;Fc为库仑摩擦力;Fs为静态黏性摩擦力;σ0为刚毛刚度;σ1为微观阻尼系数;σ2黏性摩擦因数;νs为Stribeck速度。 联立式(25)和式(32),套索传动整个过程的动态过程可描述为 (33) 为初步验证所建立的套索传动系统动态模型以及基于套索传动的人工肌肉动态模型的正确性,以试验参数为准对单套索模型以及基于套索传动的人工肌肉模型进行仿真分析。试验所用绳索直径d=1.2 mm,套管长度L=785 mm,绳索线密度ρ=0.25 kg/(100 m),套管全曲率θ=π,负载弹簧刚度KL=1.58 N/mm,串联弹性元刚度KSE=2.23 N/mm,并联弹性元刚度KPE=1.11 N/mm,系统动力学参数如表1所示。 表1 动态模型仿真参数Tab.1 Parameters of dynamic model simulation 仿真计算得套索传动动态模型的拉力和位移特性曲线如图8所示,套索人工人肌肉动态模型的拉力特性曲线如图9所示。值得注意的是:虽然试验中规定了套索输入端的位移信息为一个正弦信号,而由于套索的传递具有严重的非线性,使得套索输入力不是正弦信号,为了真实地反映套索的行为,本文在式(28)中引用了输入位移来等效表示输入力,这样可以使模型的仿真与实际情况相符。 图8 单套索传动的动态模型仿真结果Fig.8 Dynamic model simulation results of the single tendon-sheath transmission 图9 套索人工肌肉的动态模型仿真结果Fig.9 Dynamic model simulation results of the tendon-sheath artificial muscle 为了验证推导的单套索传动位移/力传递模型及影响其传动特性的因素,搭建了图10所示的单套索传动试验平台。该试验台主要由基于dSPACE在内的快速控制原型(rapid control prototype,RCP)系统、一个Maxon电机及其驱动器、两个激光位移传感器、两个拉力传感器、一根套索以及与其连接的负载弹簧组成。其中,RCP系统的软件包括Matlab-simulink、实时接口(real-time interface,RTI)模块库和dSPACE上位机ControlDesk,激光位移传感器型号为CMOS IL-300,拉力传感器的型号为SBT630。dSPACE通过CAN-open与电机驱动器实现通讯,使电机工作在位置模式下。电机通过套索按照预定轨迹拉动负载弹簧,位于套索两端的传感器用于采集系统的输入力、输入位移、输出力和输出位移,采集到的模拟量信号经过数据采集卡传输至上位机ControlDesk用于模型验证。 图10 单套索传动特性的试验平台Fig.10 Experimental platform for the single tendon-sheath transmission characteristics 本试验采取控制变量的方法来探究套索传动影响因素,参照试验组参数设置如下:输入位移10 sin(ωx)+10(mm),套管弯曲半径250 mm,全曲率为π,套管内衬材料为尼龙,预紧力25 N(预紧力定义为套索输出力的最小值)。为了验证已推导套索传动模型的正确性,将理论计算的仿真结果与参考试验组的测试结果进行比较,如图11所示。 图11 单套索传动仿真与实验对比图Fig.11 Comparison between simulation and experiment of the single tendon-sheath transmission 图11的对比结果主要反映两个现象:一是动态模型与静态模型的仿真计算结果较为接近;二是试验测量的系统输出位移略小于仿真计算值,在拉力传递特性图中这种差别主要体现在系统开始换向时,但总体上模型与试验的误差较小。前者现象的原因主要是绳索的质量较轻且属于低速传动,静态模型与动态模型相差较小。对于后者,除了由于位移传感器的挡光片无法安装在套管的端点处,造成了测量的输出位移偏小,还因信号处理中使用了滤波器导致信号失真。 此外,根据前文可知影响套索传动特性的因素主要有传动速度、全曲率ξ(L) 、摩擦因数μ以及套管半径R等,下面通过单独调整某一试验变量来进行试验分析。 (1) 角频率的影响 该组试验中角频率分别设置为0.5 rad/s,1.0 rad/s和1.5 rad/s,得到的传动特性如图12所示。 从图12中可以看出,当角频率为0.5 rad/s时其位移传递特性曲线抖动较大,这是由于速度较小,系统容易出现爬行现象。由系统力的传递特性图可以看出角频率为0.5 rad/s时,系统拉力死区最小;角频率为1.5 rad/s时,系统拉力死区最大。因此角频率增大时拉力死区也随之增大,这是由于在实际情况下套索内部存在与速度相关的阻尼力。 (2)全曲率的影响 在探究全曲率对套索传动特性影响时,试验中套管弯曲半径分别选取了π/2、π和3π/2,套索传动特性曲线如图13所示。从图13中可以明显看出,全曲率由π/2增大到3π/2过程中拉力放松死区大约从14.5 N增大到41.1 N。这是因为绳索与套管间的接触面积增大,也就导致了摩擦力的增大。 图13 不同全曲率时的位移与拉力关系图Fig.13 Diagram of displacement and tension at different total curvature 当全曲率为零时理论上就可以避免死区,但是这并没有实际的应用。因此在人工肌肉应用领域,在进行人工肌肉线路规划时应实现尽可能小的全曲率,以期达到最好的传动效果。此外,由于套管与绳索间摩擦力的增大使位移传递损失增大的同时拉力损失也随之增大,所以当全曲率变大时其最大输出力会变小,在其它试验中也出现了这种现象。 (3)摩擦力的影响 该组试验中套索的润滑条件分别设置为尼龙套管加润滑油、尼龙套管、钢制套管加润滑油以及钢制套管四种接触条件,传动特性曲线如图14(a)所示。四种条件下的拉力死区分别为25.6 N,27.4 N,49.5 N和52.9 N,可见摩擦力对套索传动性能的影响极为明显,尼龙套管相比于钢制套管其拉力死区减小明显。为提高套索的传动性能,减小死区与迟滞现象,本试验在套管中加入了润滑油, 尼龙套管与钢套管的传动特性均得到一定改善。 图14 不同材料时拉力与位移关系试验结果Fig.14 Experimental results of relationship between tension and displacement in different materials 为了便于比较不同条件下套索传动机构的位移传递特性,本文将不同试验组位移传递特性图两两进行对比,对比结果如图14(b)~图14(d)所示。可以看出尼龙套管试验组位移传递效率略高于钢制套管试验组,因此减小摩擦力可提高套索传动机构的传递效率,从其它位移对比图中均可得到相似结论。 (4)套管弯曲半径的影响 该组试验中套管弯曲半径分别设置为250 mm、200 mm、150 mm,得到的传动特性如图15所示。套管半径的变化,实际上是套管长度的变化,在拉力一定时套管总长度与套索伸长量正相关,由于绳索的刚度较大,力和位移曲线未出现明显的变化 图15 不同套管弯曲半径时的位移与拉力关系Fig.15 Relationship between displacement and tension of different casing bending radius (5)预紧力的影响 该组试验中套索预紧力分别设置为15 N,25 N和35 N,传动特性曲线如图16所示。由图可知,在实现相同目标位移的情况下,预紧力越大使得所需要的拉力也越大,其拉力死区也会相应变大。这是因为预紧力增加后,绳索和套管之间的摩擦力随之增加,位移损失也会因摩擦力的增大而增大。但考虑在实际应用中,过小的预紧力会导致套索松弛,因此在传动系统工作前有必要对其进行适当预紧。 图16 不同预紧力时的位移与拉力关系Fig.16 Relationship between displacement and tension under different preloads 为了验证套索人工肌肉模型的正确性以及探究串联/并联弹性元刚度对人工肌肉传动性能的影响,在原套索传动试验平台的基础上加入所需的弹性元件,搭建了图17(a)所示的单套索人工肌肉的性能测试试验平台。其中,主动收缩元CE模仿肌纤维为人工肌肉提供动力输入,串联弹性元SE模仿肌腱和肌纤维的弹性,并联弹性元PE一端固定,另一端通过滑块与套索单向连接,其只在人工肌肉被拉长时起作用,模仿了肌肉放松状态下的被动刚度。 图17 套索人工肌肉的试验原理及其试验平台Fig.17 Experimental principle and platform for the single tendon-sheath artificial muscle 由图17可以看出,绳索的一端与减速器相连,另一端穿过套管与人工肌肉相连,随后人工肌肉的末端连接负载弹簧。套索输入端和人工肌肉输出端安装有拉力传感器和位移传感器,用于分别测量系统的输入和输出的力、位移信号。一方面,将人工肌肉模型仿真计算结果与试验测量结果进行对比;另一方面,选择不同刚度的串联/并联弹性元件进行测试试验,采集试验中系统力与位移的数据,并对人工肌肉的传递特性进行对比分析。 定义并联弹性元与挡块开始接触时人工肌肉为原长,选择并联弹性元、串联弹性元刚度分别为1.01 N/mm和2.3 N/mm,试验测得套索人工肌肉的力/位移传递特性与仿真计算结果的对比情况如图18所示。 图18 套索人工肌肉传递特性的结果对比图Fig.18 Comparison of transmission characteristics of the single tendon-sheath artificial muscle 从图18中可以看出,套索人工肌肉的位移/力传递特性的仿真计算与试验结果基本吻合,由于套索具有明显的滞回特性,人工肌肉在收缩和放松过程中出现了与肌肉相似的滞回现象;然而由于绳索刚度较大,蠕变现象并不明显。试验结果中输出力和输出位移的最大值略小于仿真计算,其原因是除了套索传动特性的影响外,人工肌肉的加入增加了输出位移的测量结果。此外,由拉力传递特性曲线可知,当系统输出拉力小于34.3 N时并联弹性元参与作用,可以发现并联弹性元的加入在一定程度上降低了人工肌肉的传递效率,同时增大了整体的输出刚度。 为了分别探究串联弹性元刚度和并联弹性元刚度对套索人工肌肉的驱动柔顺性、传动效率等特性的影响,先后选取了不同刚度的串联/并联弹性元件对人工肌肉传递特性进行研究。将并联弹性元件的刚度设为1.01 N/mm,串联弹性元SE 的刚度分别选为1.2 N/mm,1.9 N/mm,2.3 N/mm和2.96 N/mm,所测人工肌肉的位移和拉力传递特性曲线如图19(a)所示;将串联弹性元件的刚度定为2.3 N/mm,并联弹性元PE的刚度分别选为0.37 N/mm、1.0 N/mm、1.3 N/mm和1.9 N/mm,所测人工肌肉的位移和拉力传递特性如图19(b)所示。 图19 串联/并弹性元对人工肌肉传递特性的影响Fig.19 Influence of series/parallel elastic elements on transfer characteristics of the tendon-sheath artificial muscle 由图19(a)可以看出,改变串联弹性元的刚度对位移传递结果的影响较大。具体表现为:当串联弹性元刚度降低时,输出位移与输入位移的比值变小,位移传递效率降低,套索人工肌肉表现得更柔顺;当串联弹性元刚度较大时,套索人工肌肉弹性变形量较小,输出位移更接近于输入位移,套索人工肌肉传动效率较高。因此,在实际应用中可以选择刚度合适的串联弹性元以满足不同应用场景的要求。由图19(b)可以看出,当并联弹性元刚度降低时,系统的输入位移更接近输出位移,同时拉力所受阻碍也更小,套索人工肌肉传动效率较高;而当并联弹性元刚度增大时,并联弹性元对人工肌肉的保护力度也随之提高,但是其位移和力的传动效率出现大幅度降低,因此需要综合考虑并联弹性元对人工肌肉的保护力度以及人工肌肉的传动效率选择适当的并联弹性元刚度。 本文通过理论计算与试验验证相结合的方法探究了影响套索人工肌肉传递特性的因素。根据仿真分析以及试验现象的结果可以得出以下结论: (1)全曲率一定时,位移死区随着套管半径R增大而增大,但拉力死区不受套管半径R的影响。预紧力的选择需要在满足负载要求的前提下,尽可能选择较小值。 (2)可通过增大串联弹性元的刚度提高人工肌肉的传动效率,但是串联弹性元刚度过大会降低人工肌肉的柔顺性输出;并联弹性元对人工肌肉起辅助作用,过大的刚度会导致传动效率降低,可依据现有驱动能力与负载的大小适当选择并联弹性元刚度。 (3)在系统动力学模型中,根据刚度关系将动力学模型的输入选为输入端位移,提高了模型的实用性。本文所探究的套索人工肌肉传递特性可为套索人工肌肉在工业机器人领域、医疗领域等其他应用领域提供重要的理论指导。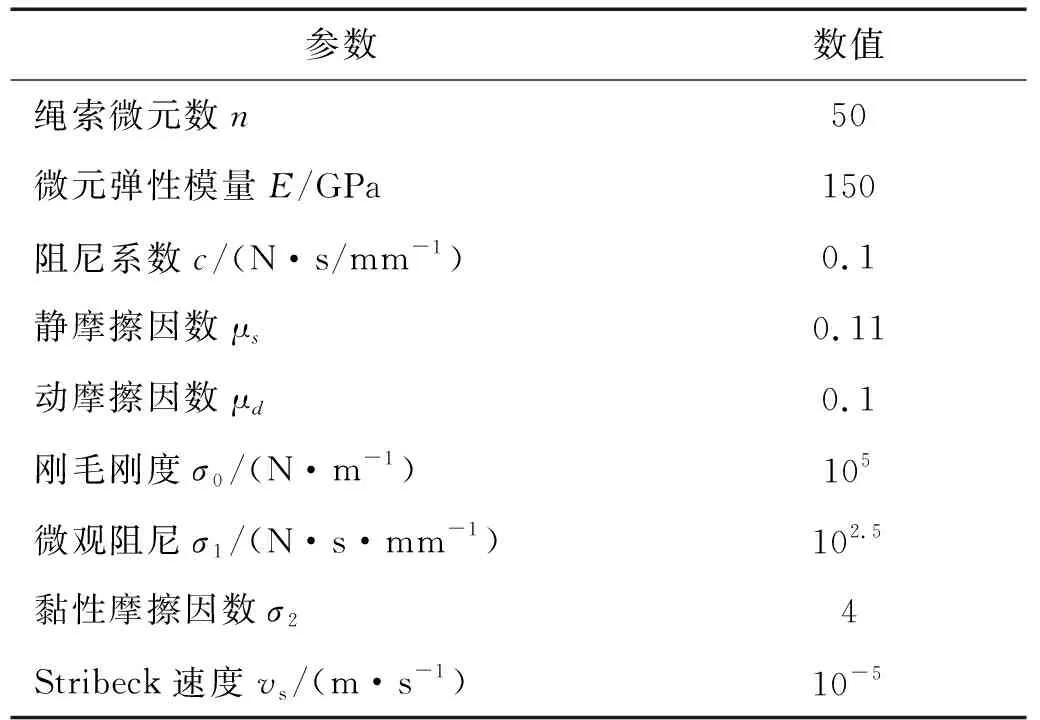


2 套索传动试验平台搭建及模型验证
2.1 套索传动特性试验平台介绍

2.2 套索传动模型验证及其影响因素分析

3 单套索人工肌肉试验平台搭建及模型验证
3.1 单套索人工肌肉的试验平台介绍
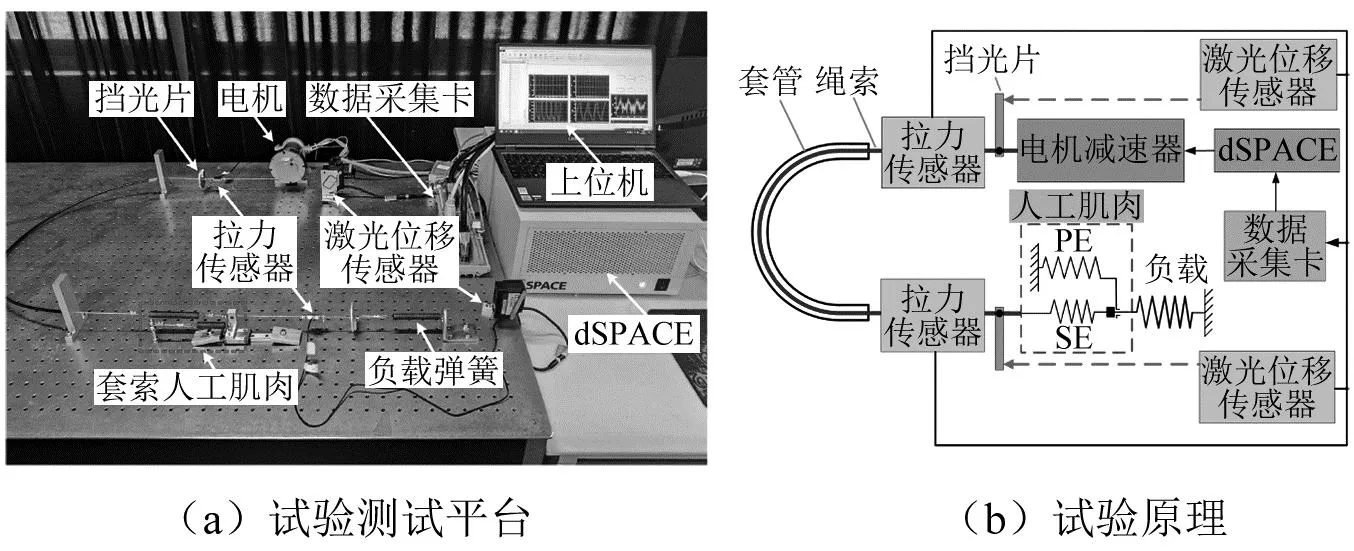
3.2 单套索人工肌肉模型验证结果分析
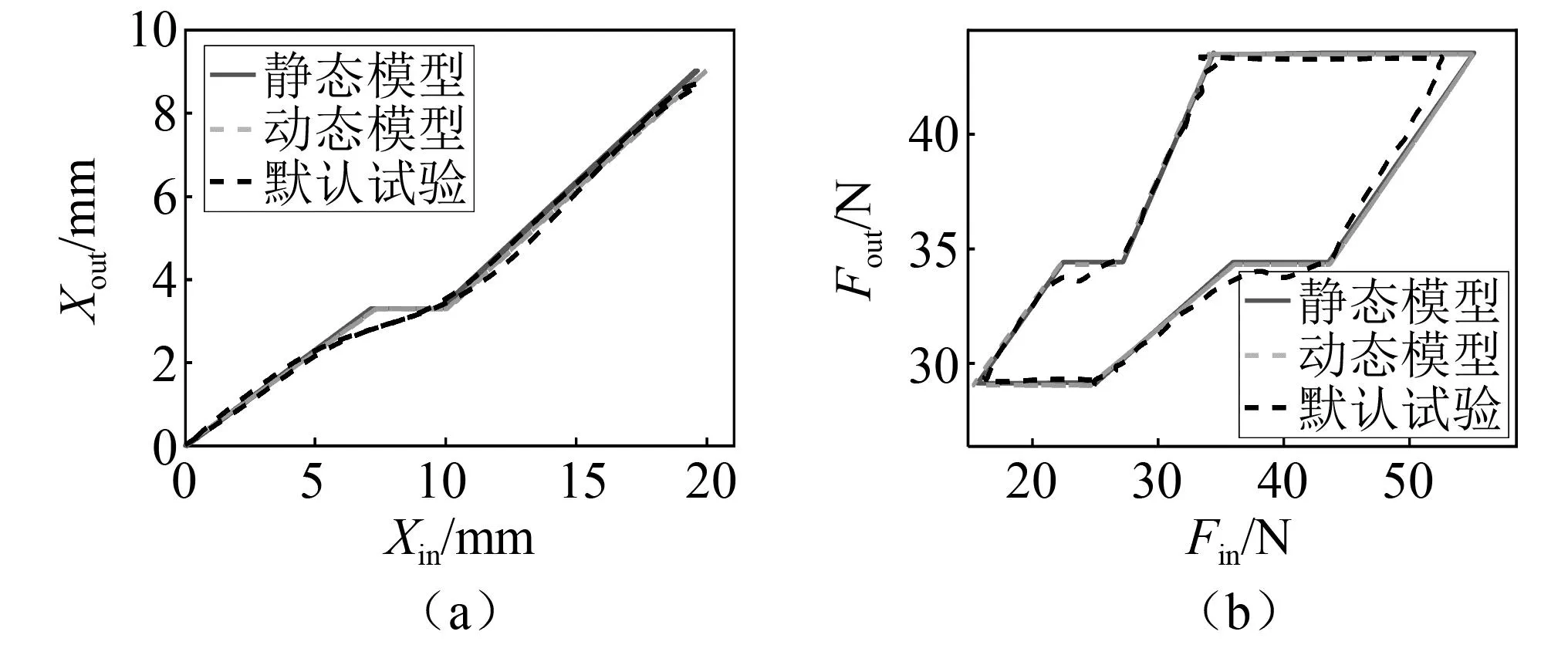

4 结 论
——一种可供多肽类药物设计和改造的多功能载体

