结构间隙对起落架地面滑跑摆振特性影响分析

阮 爽, 张 明, 聂 宏

(1. 南京航空航天大学 航空学院,南京 210016; 2. 南京航空航天大学 航空航天结构力学及控制全国重点实验室,南京 210016; 3. 南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016)

飞机在跑道以一定的速度滑行时,受到不确定激励后,机轮会偏离其所在的中间位置,围着机身轴线或支柱定向轴方向会出现强烈耦合振动,这个现象被称作摆振[1]。这种振动的方向与飞机向前滑跑的方向垂直,同时摆振的幅度急剧增加,并引发整个机体强烈晃动,情况严峻时会导致起落架结构损坏甚至引发重大安全事故[2]。

摆振是严重影响飞机正常运行的自激振动,需要采取措施避免摆振[3]。面对摆振的困扰,最合适的措施是使用减摆器[4]。为飞机安装减摆器可使摆振问题得到显著改善,但是某些飞机在滑跑过程中可能处于操纵状态[5]。

无论是使用何种方法避免摆振现象发生,都离不开间隙存在这个客观事实[6]。根据工程经验,起落架结构间隙主要体现在上扭力臂和下扭力臂的连接处、扭力臂和起落架支柱的连接处以及减摆传动系统的间隙,还有机轮轴承处的间隙[7]。

对于这些转动部件,配合间隙过小,会加大构件之间的摩擦,不利于机构运动,同时加大零件磨损[8];如果间隙过大,就无法保证运动精度,零部件剧烈的碰撞会破坏起落架的强度,缩短使用寿命。对含运动副间隙的起落架进行精确的数学建模,研究其摆振动力学特性,这对起落架的防摆及减摆设计有极其重要的意义[9]。

摆振的动力学稳定性分析具有鲜明的多维度、高耦合、强非线性特性[10],针对摆振的非线性特点,目前已有多种非线性振动分析方法,比较常见的有积分法[11]、描述函数法、多尺度法、增量谐波平衡法等[12]。近年来,利用非线性分岔理论来探究摆振领域的问题开始兴起[13]。

经过漫长的将近一个世纪的发展,利用数值分析对摆振进行稳定性研究已经非常普遍[14]。但是在一些含有复杂非线性项的模型中,要做到对摆振发生机理的深入了解还很困难,特别是对非光滑系统的研究[15]。

Zhuravlev等[16]通过试验分析间隙可能是诱导摆振的直接原因。Sura[17-18]研究了存在扭转自由间隙时系统会持续摆振的现象。Yi等[19]采用了描述函数法处理间隙模型进而进行研究。Howcroft等[20-21]建立了扭转间隙力矩的函数表达式,并将其分段函数光滑化处理,同时在主起落架摆振进行了间隙的研究[21]。Rahmani等[22]在考虑间隙的同时,也把库伦摩擦力矩同时考虑进去,一起分析两者耦合效应。

现有的文献对间隙项的研究还不充分,对间隙的认识还不够全面,尤其是回程间隙和操纵状态下的间隙影响。本文建立多维度、全面精确的起落架摆振模型,同时考虑减摆状态和操纵状态,将间隙作用形式采用函数光滑化处理,研究间隙对起落架摆振所带来的非线性影响以及对系统频域上的影响,真切地展现了结构间隙在起落架摆振中的原理。

1 前起落架滑跑状态及摆振动力学建模

1.1 起落架减摆及操纵状态简介

现代飞机一般具有两种滑跑模式:一种是减摆模式;另一种是操纵模式。前起落架操纵作动筒,如图1所示。

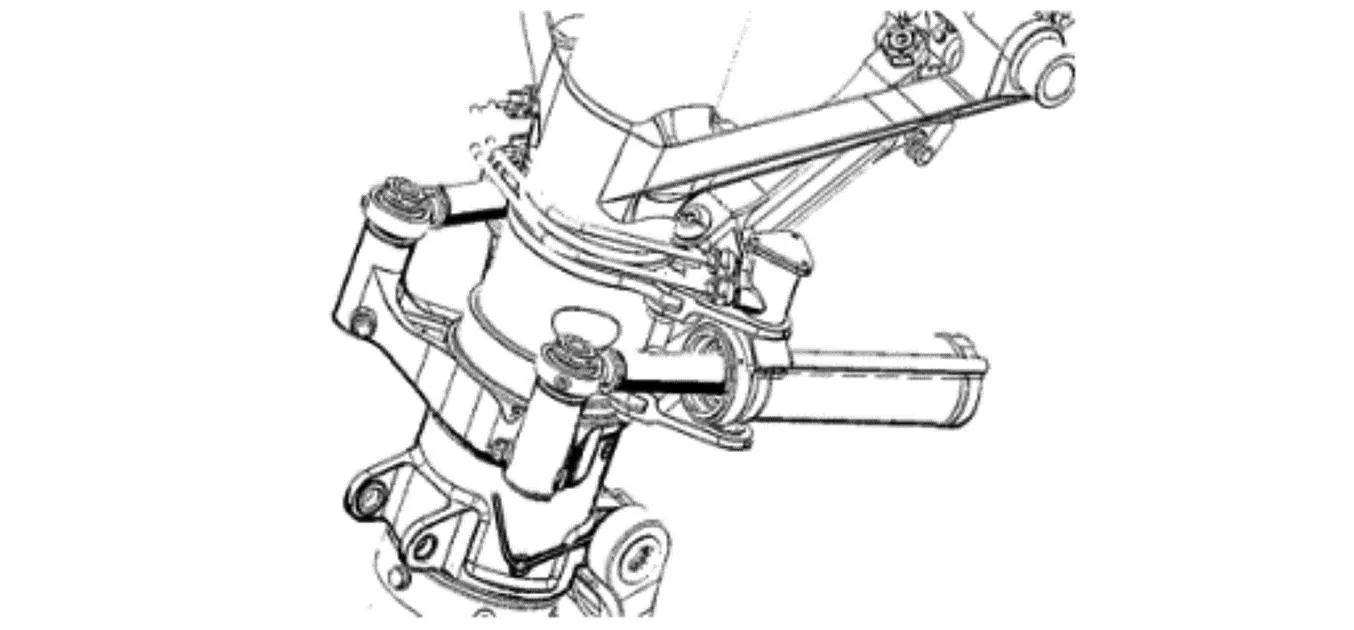
图1 前起落架操纵作动筒Fig.1 Nose gear control actuator

操纵状态是现代战斗机常有的一种状态,此状态下,飞机无论是进行直线滑跑,还是转弯操纵,均有可能出现摆振的情况。操纵模式下,起落架的转动套筒会被两个油液作动器给支撑,油液作动器中充满高压油液,导致起落架扭转方向不再自由。操纵系统原理图,如图2所示。

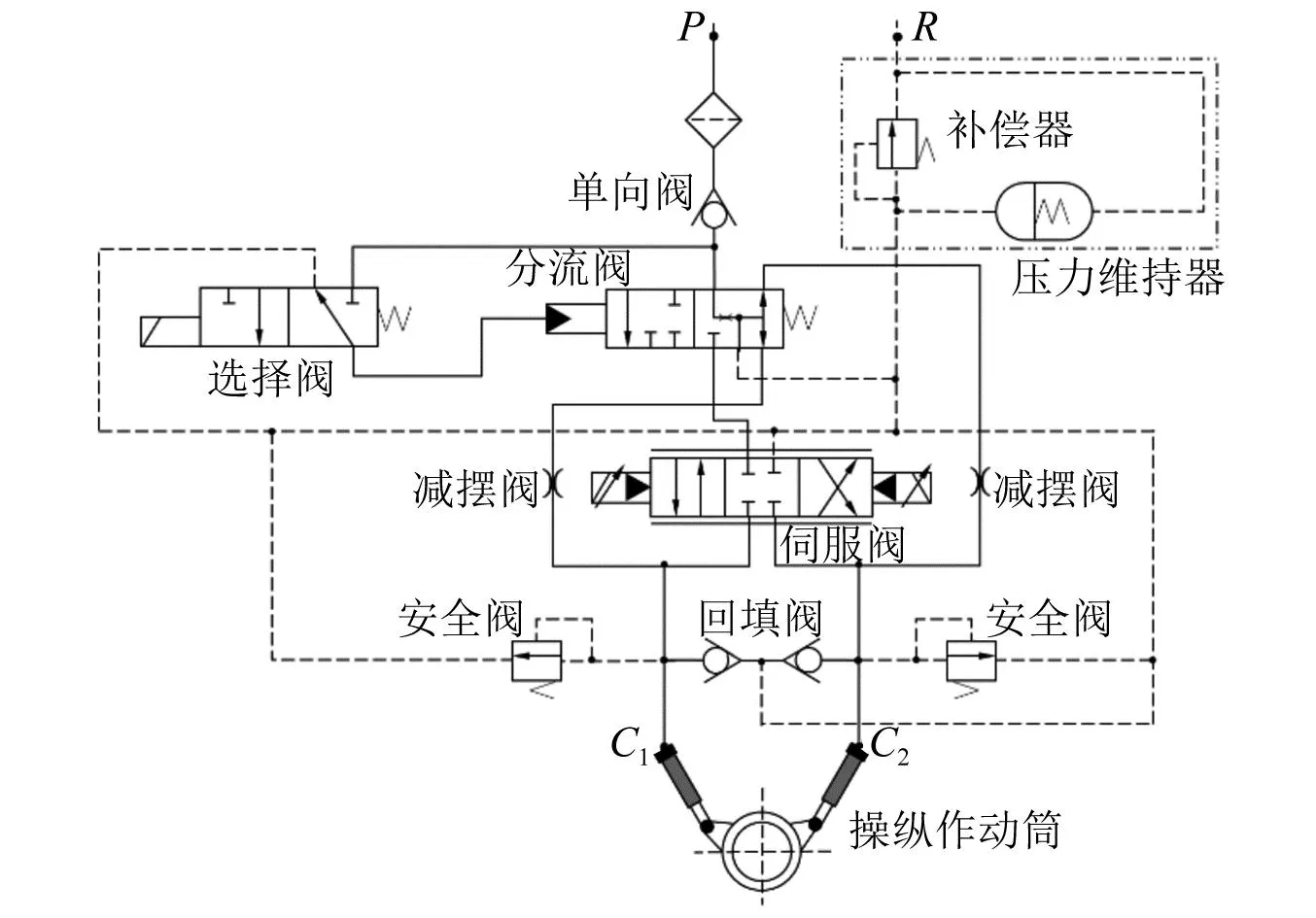
图2 操纵系统原理图Fig.2 Schematic diagram of control system

由于油液具有可压缩性,以及起落架防扭力臂自身会发生扭转变形,因此支柱相对转动时,会有一个较大的扭转阻力,阻碍起落架前轮自由偏转,此力矩与扭转角度成正比

MKψ=Kψ·ψ

(1)

式中:Kψ为操纵系统在起落架支柱扭转方向的扭转刚度;ψ为支柱扭转角。

当系统切换到减摆模式时,作动筒两腔回路接通,两个减摆阀在回路中的作用是通过自身的阻尼将液流的动能转换成热能耗散掉,从而达到减摆的目的。当支柱转动一定角速度时,假设传动比为1∶1,减摆模式产生的减摆阻尼力矩为

(2)

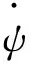
1.2 起落架间隙存在及其形式

间隙的产生有两种可能:①在起落架使用过程中,不可避免地造成一些机构的变形和磨损,产生间隙;②由于零部件的制造误差而产生的间隙,其相对于磨损所产生的间隙较小。机构存在间隙会降低零件的使用寿命,严重时导致运动副猛烈冲击和碰撞,致使机构失灵。对于机构的正常运行来讲,间隙是一个不容忽视的问题。

飞机起落架零部件结构较多,对摆振影响较大的间隙主要为各连接处间隙,如传动机构间即扭力臂一块。如图3所示,直接影响到扭转方向间隙的是下扭力臂和支柱、下扭力臂和上扭力臂、上扭力臂和套筒以及套筒和减摆装置之间的连接。间隙的传递是不连续的,是逐级递进的,但是从整体上来分析,在动力学中,可以视为是一个整体,满足叠加效应。并且这些间隙存在的部位,均是相对运动、反复摩擦的,长期磨损逐渐放大对起落架摆振稳定性的影响,因此,在起落架的设计、制造以及使用维修阶段,间隙因素都是不可忽略的关键因素之一。

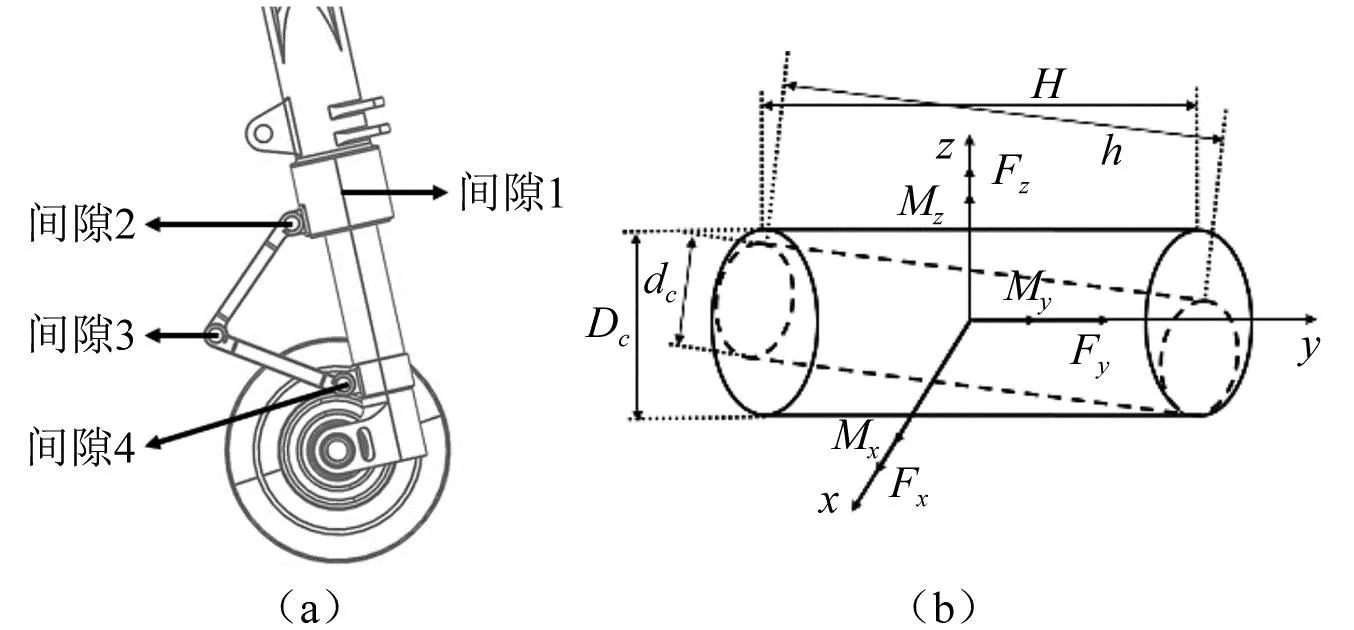
图3 间隙的位置和作用形式Fig.3 Position and action form of clearance

1.3 前起落架摆振分析数学建模

为准确描述双轮前起落架模型的基本结构和特性,本文在分析中假设前起落架支柱上端固支,忽略机身运动对前轮侧向运动的影响,建立双轮起落架摆振动力学模型,使用七个自由度用于描述前轮的摆振运动。其构型、相关变量和参数如图4和表1所示。

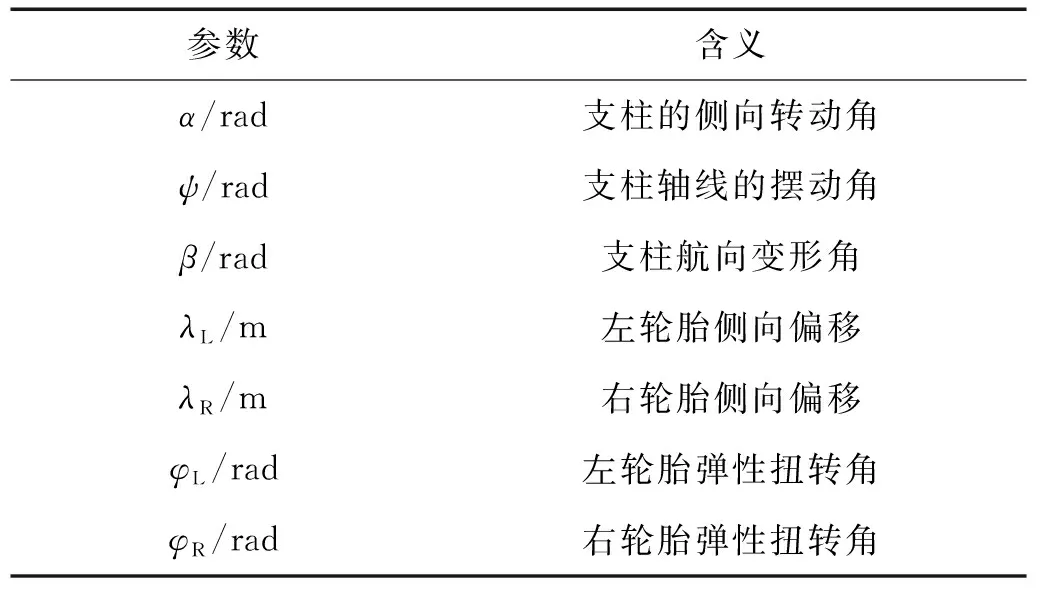
表1 自由度变量及其含义Tab.1 Degree of freedom variables and their meanings

图4 起落架摆振动力学模型Fig.4 Landing gear shimmy dynamic model

由于起落架存在前倾角,通过几何关系可得机轮摆角θ=ψcos(φ+β);轮轴倾角为γ=ψsin(φ+β);起落架的等效稳定距如下

eff=ecos(φ+β)+Rtan cos(φ+β)+
esin(φ+β)tan(φ+β)

(3)

作用在前起落架上的力矩包括惯性力矩、陀螺力矩、弹性恢复力矩以及外部作用力矩,根据动力学原理,起落架支柱侧向弯曲自由度的微分方程如式(4)所示

(4)

MλαL=MλαR=lgFKλL/Rcosθcos(φ+β)

(5)

前起落架摆振动力学模型中纵向弯曲自由度的微分方程为

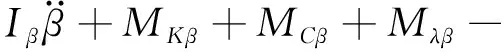
(6)

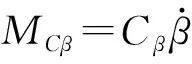
同理前起落架扭转自由度上的微分方程为

(7)

1.4 轮胎Smiley张线模型

Smiley的轮胎力学理论中,地面作用在轮胎上的力和力矩可以表示为

(8)

(9)

式中:Kλ和Cλ分别为轮胎的侧向刚度和阻尼系数;Kφ和Cφ为轮胎的扭转刚度和阻尼系数;λ和φ分别为轮胎的侧向弹性变形及扭转弹性变形。

由图5可知,λ0和φ0可以表示为

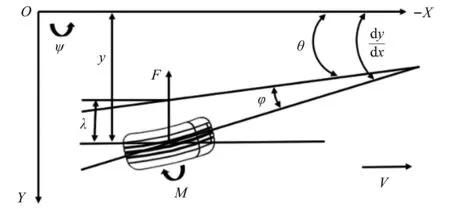
图5 轮胎模型Fig.5 Tire model

λ0=y0-(H+R)·α-effθ

(10)

(11)

Smiley利用Taylor级数将式(10)展开,忽略级数中的高次项,就可以形成轮胎近似的约束方程,本文采用Smiley的二阶近似公式

(12)

式中,L2=h(h+2σ)/2;L1=h+σ,h为轮胎触地面半长,σ为轮胎松弛长度。

通过方程协调计算得到轮胎公式为

(13)

(14)

将表示轮胎弹性力、力矩及约束条件的方程与上述平衡方程联合在一起,就形成了一组完整的、支柱上端固支的、具有双轮的前起落架摆振稳定性分析方程组。结构模型参数取值,如表2所示。

表2 结构模型参数取值Tab.2 Structural model parameter value

2 “减摆状态”含间隙摆振非线性分析

2.1 减摆状态下的间隙模型

结构间隙的存在会让减摆阻尼器的实际作用时间减少。当支柱转角达到最大值,开始往另一个方向偏转时,由于间隙的存在,实际上减摆器并没有起到作用,等支柱转过间隙值角度后,再通过扭力臂等机构带动减摆器运动,减摆器此时发挥其真正的作用,如图6、图7所示。

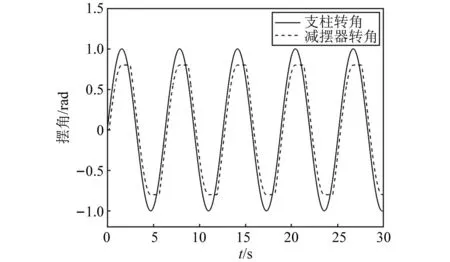
图6 起落架相关角度变化Fig.6 Landing gear related angle change

从图6中可以看到,减摆器的转动会随着支柱转动而转动,但是在支柱转角变向的情况时,减摆器有一段非工作时间,这种间隙称之为回程间隙,回程间隙的研究无法进行光滑化系统处理,在以前论文中鲜有研究,因此对回程间隙的分析十分有必要。

2.2 间隙对系统稳定性的影响

间隙的存在会真实地减弱阻尼器的作用,为便于从理论上对间隙因素进行分析,模型中只存在间隙为零和不为零的情况,并且存在间隙时,扭转角小于间隙值的部分,减摆阻尼系数设置为零,如图8所示。

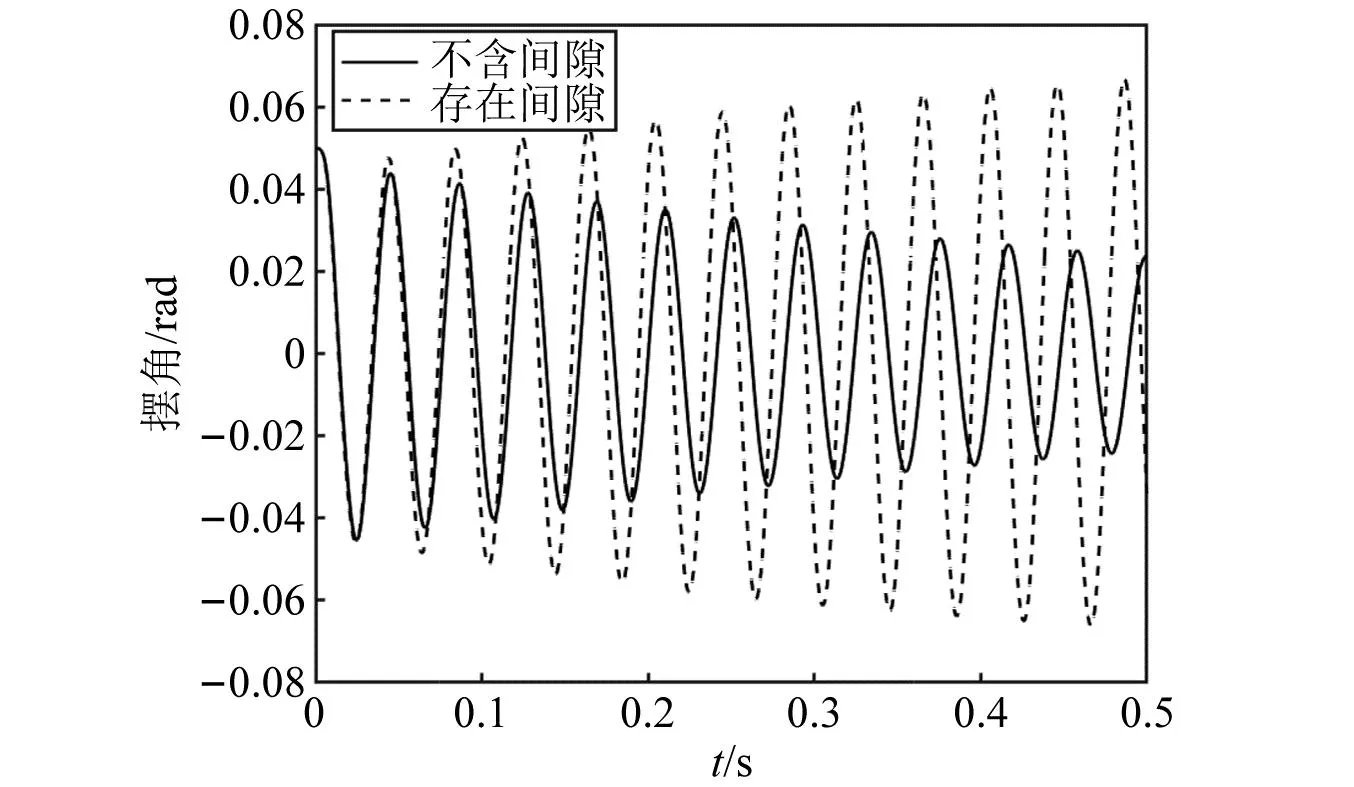
图8 间隙对稳定性的影响Fig.8 Effect of clearance on stability

由于间隙的存在,减摆器提供的阻尼系数可等效为一个更小的阻尼系数,摆角的幅值角度较小时,其等效的阻尼不满足系统稳定的阻尼值,因此会出现发散状况。存在间隙后,其摆振频率会略微增大。

随着摆角的增大,间隙占比有限,特别是对于转角处,其角速度本身就较小,影响会越来越弱。故增大阻尼系数进行数值分析如图9所示。

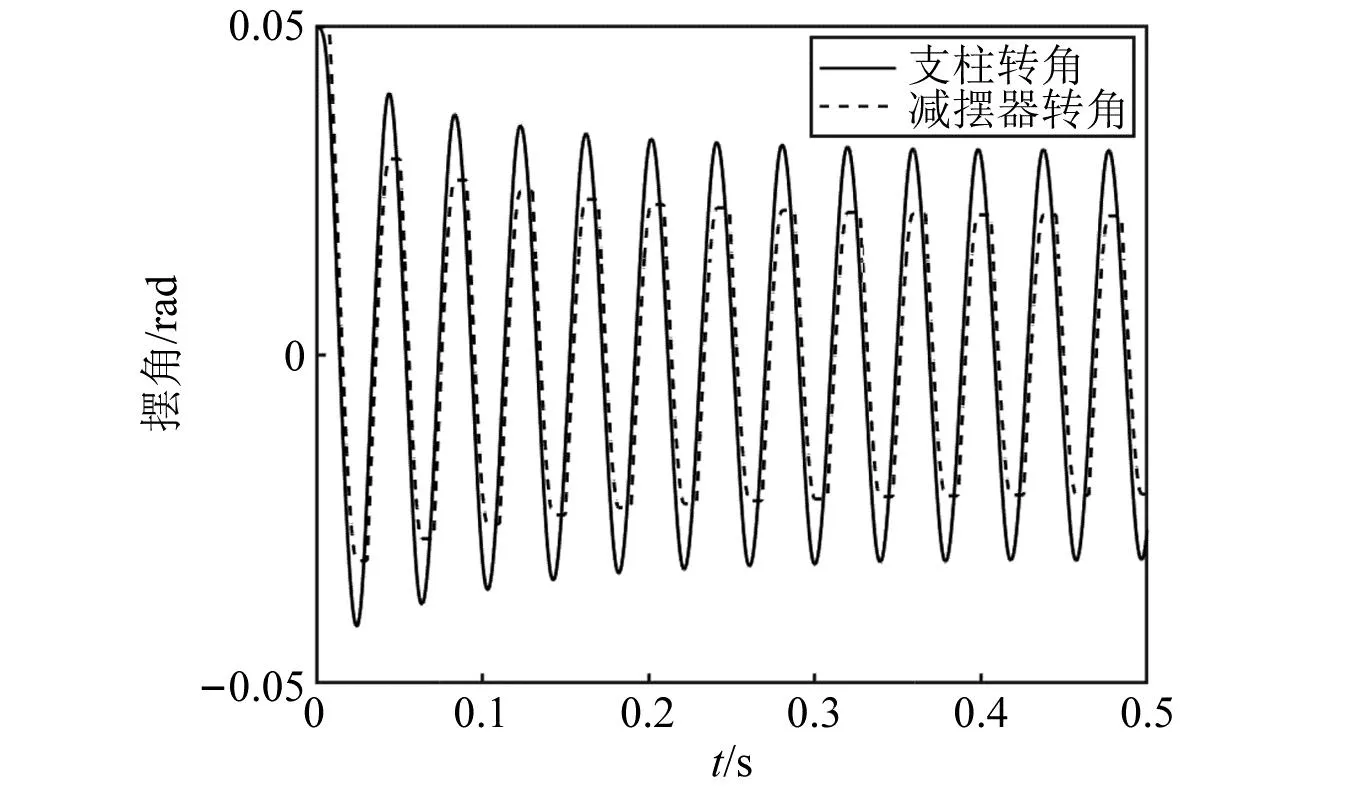
图9 含间隙起落架摆振曲线Fig.9 Shimmy curve of landing gear with clearance

观察支柱转角以及减摆器转角可以发现,整个起落架处于一个稳定的震荡状态。值得注意的是,扭转间隙值的大小对摆振稳定区域并无影响。只要扭转间隙大于零,不同取值得出的摆振区域是完全重合的。

2.3 间隙与极限环的相互关系

上述分析已经不是线性系统所能解释清楚的,此处基于分岔理论,分析间隙对系统稳定性的影响,计算在不同间隙值情况下动力学特性以及间隙值对摆振振幅的影响探究。

不同于普通摆振的极限环,含间隙摆振极限环具有一定的不连续现象。从力学本质上看,起落架机轮自激型摆振是一种动力学失稳现象,当结构存在间隙时,支柱轴的摆动不再是渐进稳定的,而进入一种极限环震荡现象。从数学上看,描述摆振系统的数学方程的解的拓扑结构发生了变化,出现分岔现象。从定性上看,摆振类似于非线性系统的霍普夫分岔现象,如图10所示。

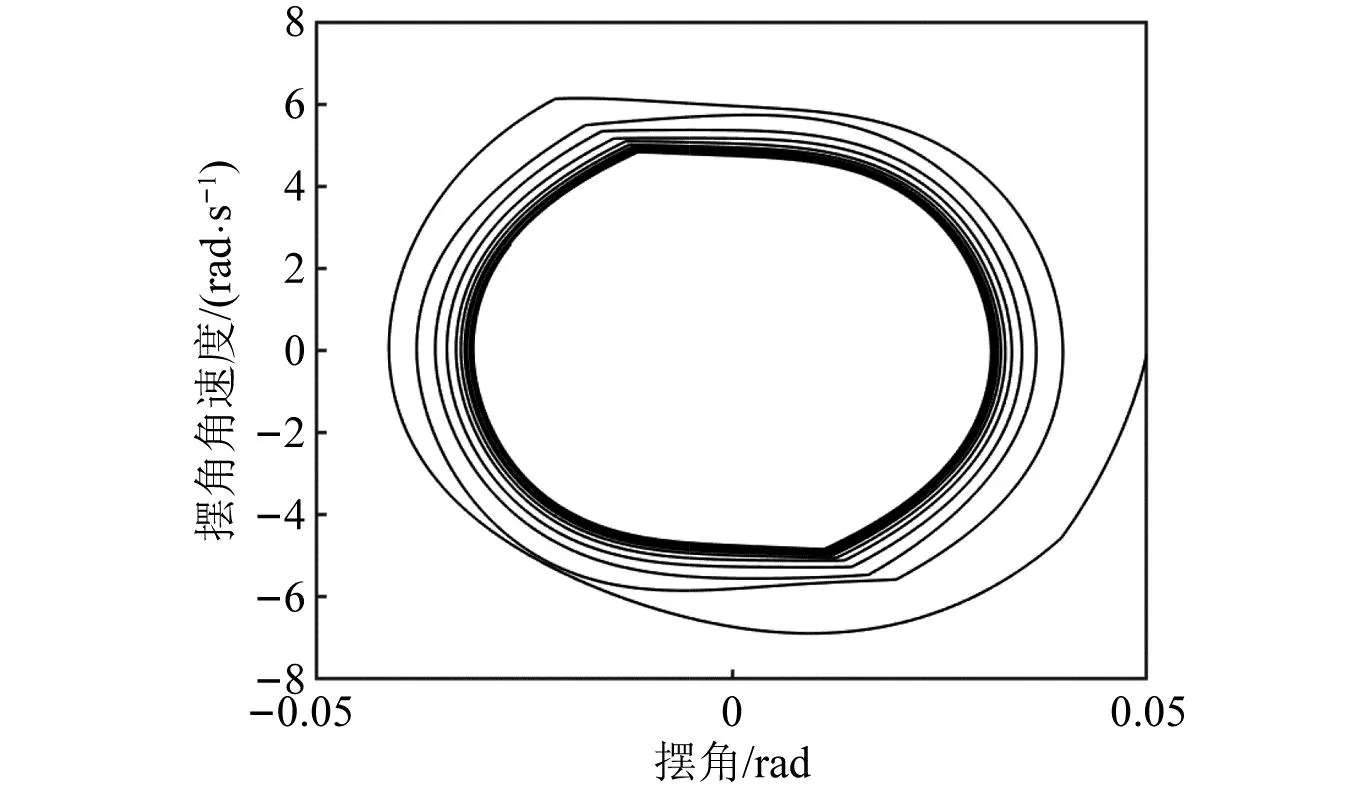
图10 含间隙摆振极限环Fig.10 Shimmy limit cycle with clearance

为研究减摆阻尼系数以及间隙值的大小对起落架摆振极限环的影响,设置满足稳定裕度的阻尼系数以及不同大小的间隙值,数值求解其稳定的极限环振幅数值,结果如图11和图12所示。

图11 阻尼系数对振幅的影响Fig.11 Shimmy limit cycle with clearance

图12 间隙值大小对振幅的影响Fig.12 Shimmy limit cycle with clearance

对于相同间隙值,随着减摆器减摆阻尼系数的增大,其稳定后的极限环振幅是越来越接近间隙值的。对于不同间隙值大小,其振幅和间隙大小关系近似成正比。所以在一些特定飞机,随着滑跑次数的增多,机构零部件叠加的间隙越来越大,其发生摆振的几率会增大且其摆振的幅值也随着增大,对飞机滑跑产生更加恶劣的影响。

2.4 含间隙下库伦摩擦的作用

库伦摩擦普遍存在于起落架系统,由于支柱表面的不光滑,以及结构间存在的灰尘等都不会使扭转阻尼严格为零,只要接触界面存在相对滑动,并且具备一定接触力,就一定存在库伦摩擦作用。库伦摩擦恰好可以实时提供与运动方向相反的摩擦力矩来耗散能量。

为方便研究运算以及解决角速度在零值点的不可导问题,采用反正切函数来模拟库伦摩擦力矩

(15)

式中:M0为库伦摩擦力矩大小;ks为一取值为正的无量纲参数,定义为阶跃模拟系数。

如图13所示,当取1 000时就可以大致描述库伦摩擦的影响作用,取值过大会造成系统运算负担,仅仅略微改变系统的计算结果的精度。在采用式(15)来表示库伦摩擦力矩后,动力学方程不光滑的现象得以改善。对比考虑间隙情况下,库伦摩擦对系统的影响如图14所示。

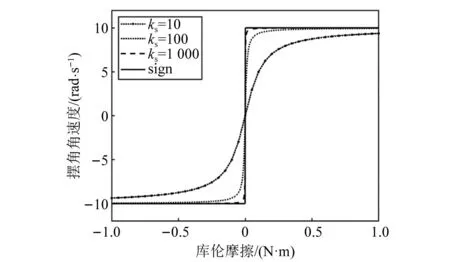
图13 正切函数近似阶跃函数示意图Fig.13 Schematic diagram of approximate step function of tangent function

图14 库伦摩擦对含间隙系统的影响Fig.14 Influence of Coulomb friction on system with clearance

由图14可知,由于库伦摩擦的存在,一定程度弥补了减摆器非工作状态下系统稳定所需的阻尼力矩,系统并没有出现震荡的情况。因此可以推测,起落架系统在结构间隙较小时,库伦摩擦作用能够避免系统出现摆振现象。

3 “操纵状态”含间隙摆振特性分析

3.1 操纵状态下的间隙模型

操纵状态下,当起落架系统存在结构间隙时,起落架支柱的有效扭转刚度会急剧降低,当扭转角的幅度没有间隙大时,支柱的扭转刚度和扭转阻尼均不产生效果。假设扭转自由度存在扭转间隙,其间隙数值大小是关于扭转轴正负各。扭转角度的绝对值大于时,扭转力矩起效;反之,则失效。此处的扭转力矩设置为线性扭转阻尼,且不考虑库伦摩擦与平方阻尼的作用,扭转作用力可表示为

(16)

图15为不同大小间隙值情况下支柱刚度作用的分段函数曲线。虽然扭矩连杆自由间隙的非光滑模型给出了扭矩连杆自由间隙区域上接触动力学的简单表示,在实践中,物理系统中自由间隙和接触区域之间的过渡不太可能是真正非光滑的。相反,灰尘、油脂的存在以及扭矩连杆组件的退化和磨损等因素都会导致在顶点接头内产生阻力和耗散力。因此,系统的真实动力学将不同于理想的非光滑情况。

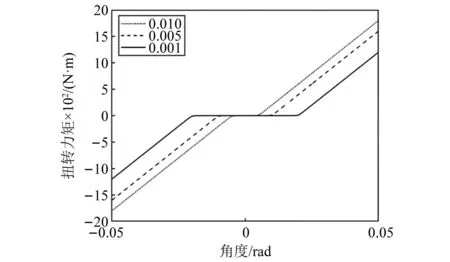
图15 包含间隙项的支柱扭矩示意图Fig.15 Strut torque diagram with clearance items

从零刚度到非零刚度的非常快速的过渡,虽然仅仅在间隙小且有限范围内发生,但是为反映这一行为,本文将上述公式的平滑表示,引入平滑参数,函数可以表示为

(17)

如图16所示,随着平滑参数越来越小,函数越来越接近光滑情况。

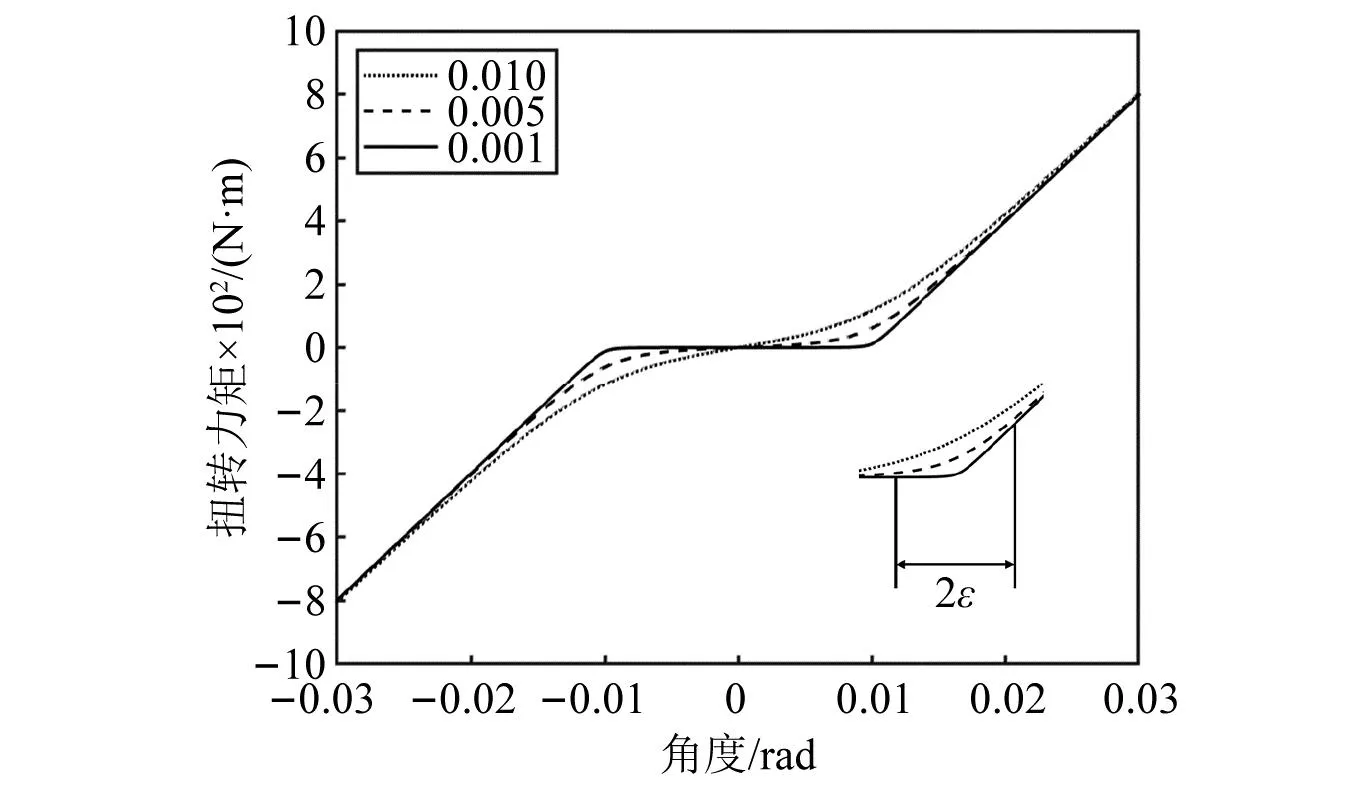
图16 支柱扭矩拟合示意图Fig.16 Schematic diagram of strut torque fitting

3.2 含间隙摆振特性分析

自由间隙的存在会真实地影响扭转刚度的作用,只有当轮摆角幅度超过间隙值,支柱的扭转刚度和扭转阻尼才会共同作用来抑制摆振产生。反之,两者在摆振中不产生任何作用。

图17中:实线为支柱的真实转动角度;而虚线则代表起落架扭转刚度产生作用的角度。系统保持着持续震荡的状态,其幅值略大于间隙值。

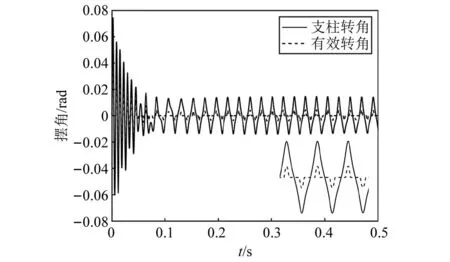
图17 含自由间隙摆振曲线Fig.17 Shimmy curve with free clearance

不难发现在曲线的姿态中,当支柱转角小于间隙值时,其斜率即角速度的变化存在变速的情况,为方便研究其角速度和角度的关系,绘制其相图进行研究分析:

与一般振动稳定极限环不同,虽然系统表现出持续震荡的状态,但是其相图并不是一个环状结构。从图18可以发现,当处于扭转刚度非作用状态时,支柱角速度是先减小后增大的;当系统从零刚度状态过渡到非零刚度状态时,起落架的摆角变化很小,但是角速度很快地就反向了,使系统不再发散。

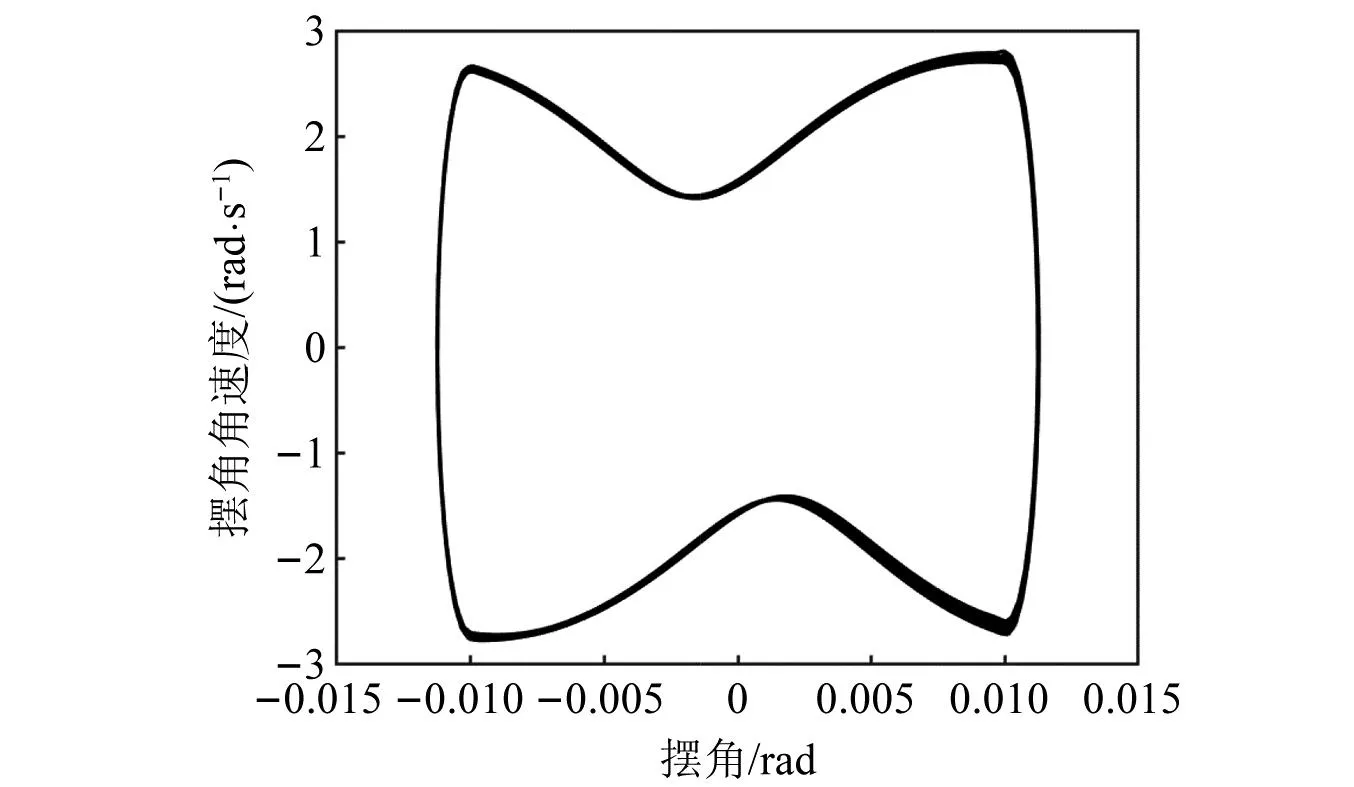
图18 摆振相图Fig.18 Pendulum phase diagram

从图19中可以看出,系统最初的频率明显低于后续震荡的频率,这是由于最开始系统扭转间隙未起作用,系统主要是扭转方向轮胎的摆振,俗称“轮胎型摆振”,后续由于扭转刚度开始发生作用,系统的扭转方向的刚度变大,系统整体上开始耗散能量,与间隙作用时自激振动的能量平衡,系统能够保持稳定的震荡状态。

图19 小激励下的摆振Fig.19 Shimmy under small excitation

3.3 耦合效应的频率分析方法

快速博里叶变换(fast Fourier transformation, FFT)算法,可以将时域信号变换到频域。设置不同的扭转方向刚度,系统呈现两种振动状态:一种是减摆状态下,自由振动频率;另一种是操纵状态下,具有较大的支柱振动频率,时域曲线可以验证FFT算法对频域计算的可靠性。

改变扭转方向刚度,观察系统频率变化如20图所示。

图20中,随着扭转刚度的增大,系统的摆振频率也增大,因为起落架主要性状是个二阶耦合系统,因此会出现两个振动频率。当扭转刚度相对侧向刚度较小时,由于侧弯刚度相对较大,变形较小,体现的是轮胎绕轴旋转变形的振动频率;当扭转刚度较大时,支柱侧弯方向较大振动的频率会显现出来。飞机摆振是两者相互作用的结果,扭转刚度越大,其扭转方向的振动越发明显,且振动频率也会增大。

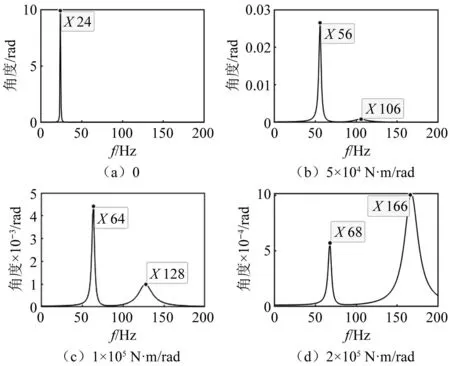
图20 扭转刚度对频率的影响Fig.20 Influence of torsional stiffness on frequency

改变侧弯方向刚度,观察系统频率变化如图21所示。

图21 侧弯刚度对频率的影响Fig.21 Influence of lateral bending stiffness on frequency

侧弯刚度的增加,可以增大起落架整体的摆振频率。从幅值上来看,由于侧弯刚度的增加,扭转刚度相对侧弯自由度而言变弱了,因此高频扭转方向的振动会变得不再明显。因此在设计起落架时,应该更多地考虑侧向刚度的数值,不然扭转方向刚度过大会引起高频的支柱型摆振,对起落架的功能、寿命等其他因素极其地不利。

3.4 含间隙情况下的时频分析

结构间隙的存在会让扭转刚度处分为零刚度和非零刚度的情况,但它只针对扭转方向的刚度和阻尼,对轮胎的变形以及支柱的变形不产生直接影响。考虑扭转间隙后,假设起落架在扭转正负方向存在间隙值为的自由间隙。首先从时域上研究间隙大小对摆振的影响,设置不同的间隙值,数值分析得到如图22所示曲线。

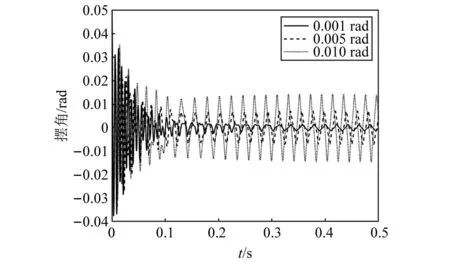
图22 不同间隙值的时域曲线Fig.22 Time domain curves with different gap values

由图22可知,系统首先出现的是高频振动,最后慢慢趋于临界稳定。随着自由间隙值的增大,系统的震荡幅值增大,系统始终出现摆振现象,振幅略大于间隙值。从频率上看,几乎没有任何改变,故使用FFT算法对不同间隙摆振工况进行频域分析得如图23所示。

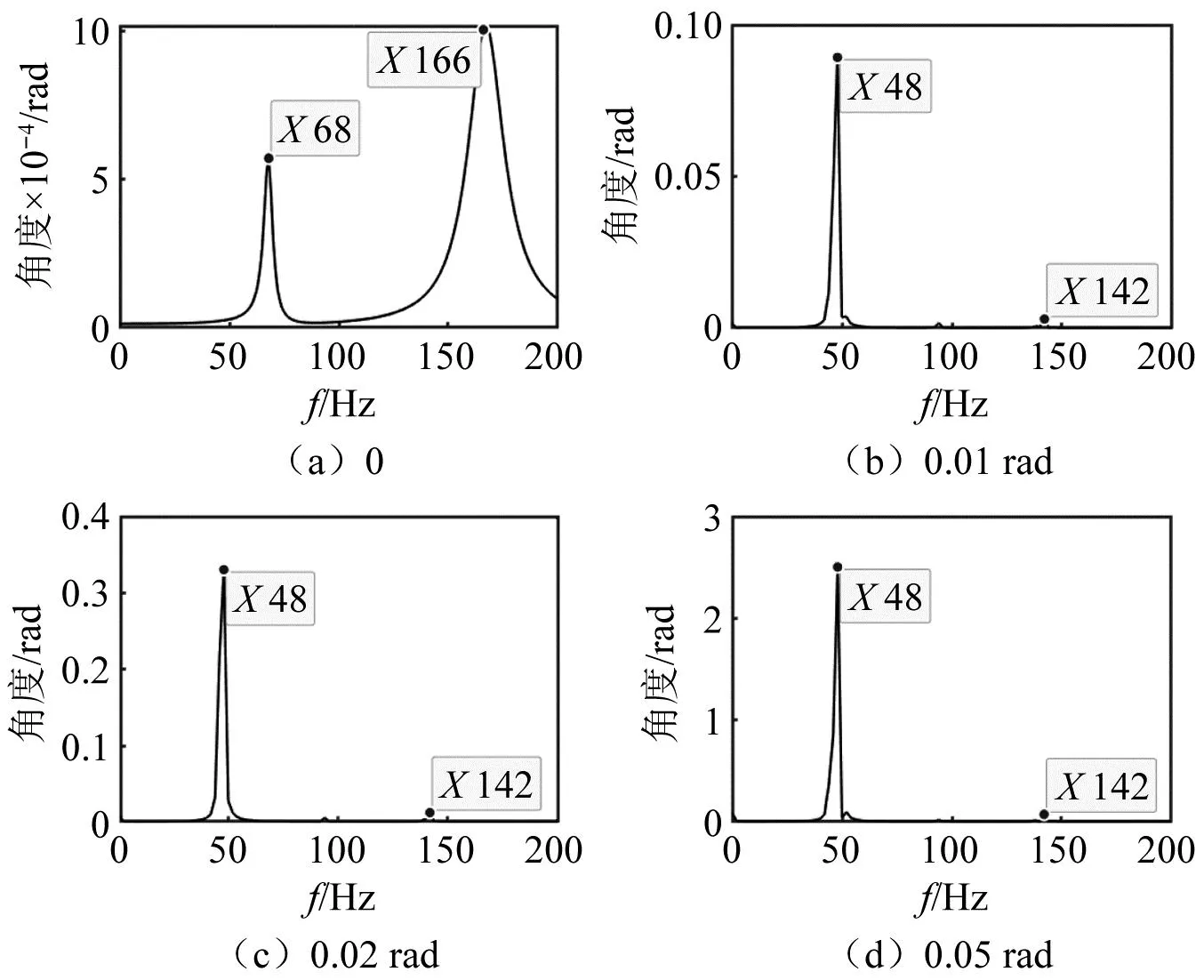
图23 间隙对频率的影响Fig.23 Effect of gap on frequency

频域分析发现,不含间隙时,起落架摆振显示68 Hz和166 Hz振动频率,这是纯操纵状态下的系统摆振频率。含间隙系统的摆振频率均处于48 Hz以及142 Hz。

为探究其缘由,此处将扭转刚度、间隙值以及振幅记录如表3所示。

表3 刚度、间隙与振幅的关系Tab.3 Relationship between stiffness、clearance and amplitude

从表3中看出,扭转刚度越大,其振幅会减小,且振幅大小和间隙大致成正比的关系,可认为操纵状态油液扭转力矩的有效作用区间和非作用区间的比值是大致固定的,数据上可解释图23间隙数值的变化并没有导致系统频率的变化的正确性。

存在结构间隙后,起落架系统变成两个振动的叠加态,一个是不稳定的自激振动状态,另一个是收敛的操纵状态。间隙数值的变大会增大自激振动的幅值,影响摆振的角速度,导致系统的能量会增大,相应地,操纵状态是耗散运动的能量,那么肯定有一个平衡点使得操纵状态下阻尼耗 散的能量等于自激摆振状态下系统产生的能量,由于模型中两个振动状态各自的振动系统非线性比较弱,所以无论任何间隙数值大小,系统在稳定的等幅振荡的情况下,两种状态作用时间的占比大致不变,因此理想状态下频率不会受到间隙数值的影响。

上述模型和分析均是基于理想状态,实际上由于非线性阻尼、库伦摩擦、碰撞等因素的存在,当系统存在间隙的时候,其产生阻力和耗散力会耗散系统整体动能,影响系统的振动频率。

4 结 论

本文建立了多自由度双轮起落架动力学模型,对数学模型进行光滑化处理,应用数值分析以及频域分析的方法,模拟了不同状态下,起落架含间隙的摆振动力学过程,并对其特性进行分析。

(1) 减摆状态下,起落架间隙的存在会使起落架出现持续震荡的情况,且摆振频率略微增大,扭转间隙值的大小对摆振区域并无影响。间隙型摆振类似于非线性系统的霍普夫分岔现象。

(2) 减摆状态下,由于库伦摩擦的存在,弥补了间隙情况下减摆器非工作状态,系统也不会出现震荡的情况。间隙增大到一定值,库伦摩擦难以满足稳定要求时,飞机仍旧会出现摆振现象。

(3) 操纵状态下,自由间隙的存在会真实地影响扭转刚度的作用,只有当轮摆角幅度超过间隙值,支柱的扭转刚度和扭转阻尼才会共同作用来抑制摆振产生。系统保持着持续震荡的状态,其振动幅值略大于间隙值,并且与扭转刚度有关。

(4) 操纵状态下,通过对系统进行频域分析,系统有两个固有振动频率,理想情况下,存在间隙后,系统振动频率降低,振动幅值随着间隙的增大而增大,但是系统振动频率不会随着间隙大小的变化而明显发生改变。