桥梁风工程研究中的雷诺数效应研究进展
刘庆宽, 韩 原, 孙一飞, 郑云飞
(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043; 2.河北省风工程和风能利用工程技术创新中心,石家庄 050043;3.石家庄铁道大学 土木工程学院,石家庄 050043; 4.石家庄铁路职业技术学院 铁道工程系,石家庄 050043)
随着大跨度桥梁跨度的日益增大,主梁和桥塔、斜拉索等构件上的风荷载和风致振动问题日益突出,大跨度桥梁风致振动事件引起广泛的社会关注,如2020年鹦鹉洲大桥、虎门大桥、西堠门大桥先后发生了涡激振动现象[1-3]。为了研究和解决桥梁的风荷载和风致振动问题,常用的研究手段有现场实测、数值流体计算和风洞试验。
风洞试验在大跨度桥梁抗风验算和设计中起着重要的作用。风洞试验中需要遵守相似准则,雷诺数作为风洞试验相似理论中的最重要参数之一,其准确模拟对于试验结果的准确性具有十分重要的意义。由于风洞尺寸和试验风速的限制,一般风洞试验的雷诺数远小于实际桥梁的雷诺数,因此,研究表征桥梁结构和构件的风荷载与风致振动相关特性的参数随雷诺数的变化规律,对于判定试验结果的准确性和可靠性,具有重要的研究意义和工程应用前景。
对于桥梁风工程研究中涉及到的各种雷诺数效应问题,尽管已经取得一定的成果,但是由于影响雷诺数效应的因素很多,仍有许多问题值得进一步深入研究和探讨。本文介绍了雷诺数效应问题的由来,分析了雷诺数的影响因素,从静力、流场、风致振动等方面,系统总结归纳了桥梁风工程研究中雷诺数效应相关的研究成果和最新进展,指出了依然存在的若干问题,为相关的研究和工程应用提供依据和参考。
1 雷诺数的由来和影响因素分析
早在1883年, Reynolds[4]指出闭口管道中水的流动状态为层流、过渡流还是湍流,取决于水的密度ρ、黏性系数μ、流速U和管道的内径D。随后, Rayleigh[5]引入圆柱体的外径D作为特征尺寸,以ρUD/μ的形式将上述参数进行无量纲化组合,用以表示惯性力和黏性力之比,并将该组合参数应用于球体和柱体的绕流问题。阿诺德·索末菲于1908年将无量纲参数ρUD/μ命名为“Reynolds number”,Von Karman[6]用“Re”作为“Reynolds number”的简写,并引入运动黏性系数ν=μ/ρ,则雷诺数的表达式Re=UD/ν。这就是如今常用的雷诺数表达式。
在之后开展的钝体绕流研究中,人们发现物体周围的流场状态同雷诺数的大小存在较强的依存性[7-8]。不同雷诺数下,物体周围的流场和对应的气动力、涡脱特性等都可能发生显著变化。因此,在以风洞试验、水槽试验为主要研究手段的流体力学、空气动力学和风工程的研究中,试验雷诺数和实际雷诺数的相似成为相似准则中需要重点考虑的问题。
从雷诺数的表达式Re=UD/ν[9-12]来分析三方面因素对数值大小的影响。
首先分析黏性系数μ和运动黏性系数ν=μ/ρ。对于黏性系数,根据萨瑟兰公式,当压强不变时,可通过式(1)计算
(1)
式中:ρ0为17.16×10-6Pa·s;T为绝对温度;T0取值273.15 K;c取值110.6 K。
当压强的数值变化不太大时,压强对黏性系数的影响很小。
流体密度与环境(温度、湿度、气压、海拔、纬度等)有关。对于空气密度来说,其与温度、湿度和气压的关系可用式(2)表达
ρ=0.003 484 3(p-0.377 9φps)/T
(2)
式中:ρ为空气密度;p为大气压强;φ为相对湿度;T为绝对温度;ps为饱和水蒸气分压力。
ps=Aitk(i=1,2,…,5)
(3)
式中:Ai为常数,数值分别为44.327 6,1.421 3,0.026 8,2.784 27×10-4,2.67×10-6;ti为温度。
分析式(1)和式(2)可知运动黏性系数分别随温度和相对湿度单调增加。为了直观掌握环境对运动黏性系数的影响,分别取两组差异较大的参数,取气温t=-10 ℃、相对湿度φ=0和气温t=40 ℃、相对湿度φ=90%,算得运动黏性系数分别为1.241 8×10-5和1.907 6×10-5,后者约为前者的1.5倍。因此,当试验环境为自然环境时,因季节改变而引起的温度和湿度变化所导致的运动黏性系数的变化范围有限,不会产生数量级的差别。
其次,对于Re=UD/ν分子中的速度项,由于受到风洞设备和性能方面的限制,来流速度U通常比实际的数值小很多。对于桥梁风洞试验来说,用于全桥模型和节段模型振动测试的常用风速一般在20 m/s以内,风洞的最大风速一般在40 m/s左右,风速方面除了电机调速范围、常用风速、功率等许多因素之外,马赫数不能超过0.3也是限制因素之一。
最后,对于Re=UD/ν分子中的特征尺寸项,受到试验断面尺寸、阻塞度的要求和模型刚度的要求等限制,试验模型比实际结构要小1~2个数量级,因此试验中雷诺数表达式的分子项数值通常比实际数值小若干数量级。以1 ∶1 000缩尺比的全桥气弹模型试验为例,根据几何缩尺比可以算得试验风速为实际风速的1/10,在不考虑运动黏性系数影响时,试验雷诺数为实桥雷诺数的1/1 000。如何缩小两者的差别,或者在无法缩小差别的情况下,如何利用试验结果来准确反映实际结果,一直是该领域重要的研究课题。
2 桥梁结构雷诺数效应的原因分析
风荷载和风致振动问题是大跨度桥梁设计中需要重点考虑的问题。在设计阶段,通过风洞试验或其它方法准确掌握风荷载的大小,明确是否发生风致振动问题,对于大桥设计的安全性和经济性具有重要的意义。
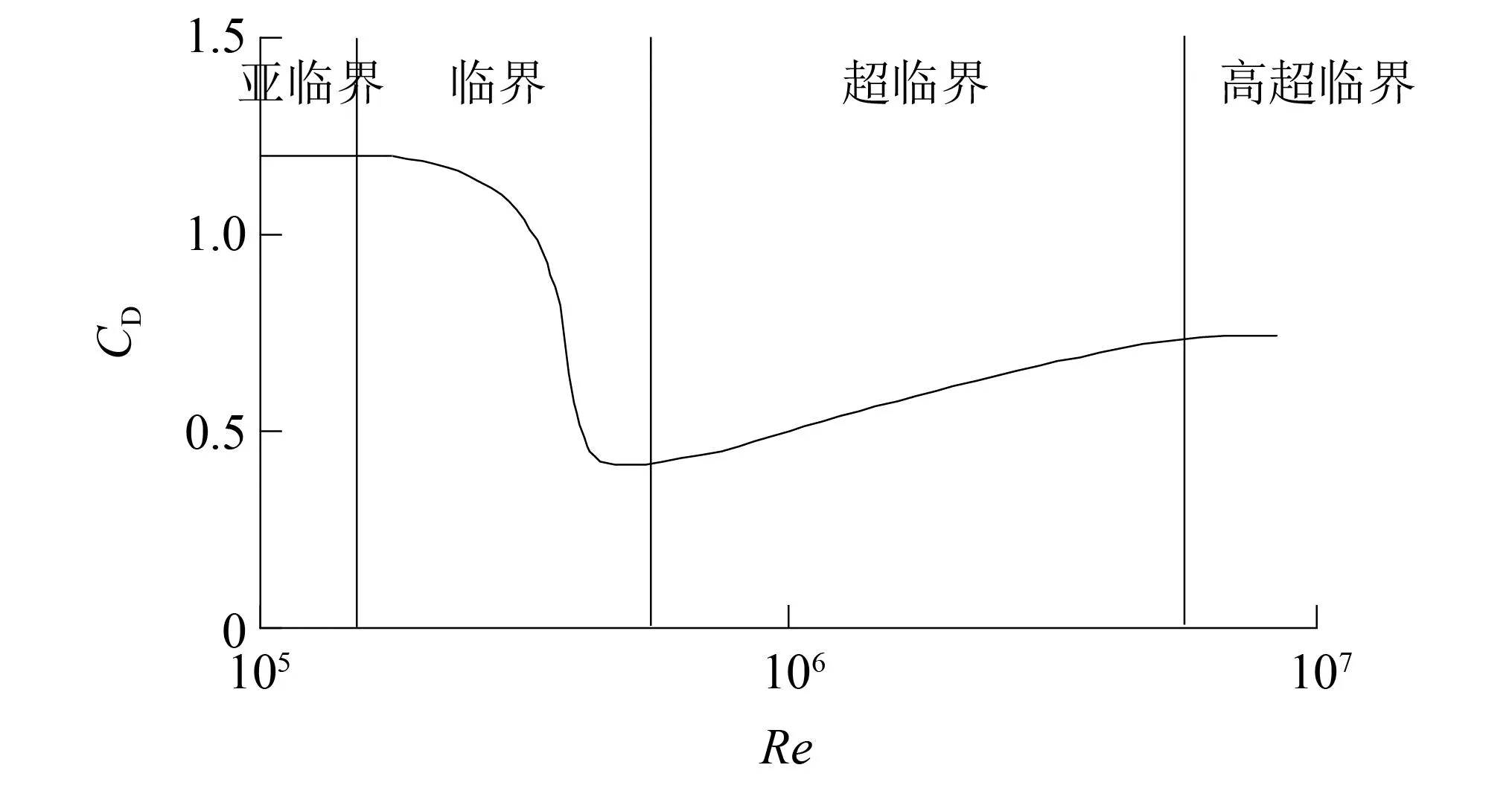
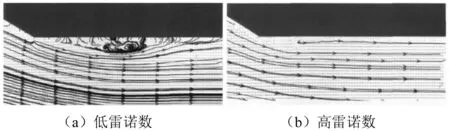
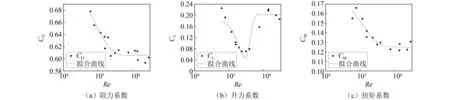
虽然斜拉索、桥塔、主梁等不同断面形式的结构,在低雷诺数一定范围内,静力三分力系数、表面压力系数及其分布、流场结构、振动特性等气动特性不随雷诺数变化;但是,在较高雷诺数范围内,桥梁结构的气动特性随雷诺数变化而变化。这种气动特性随雷诺数变化的规律即桥梁结构的雷诺数效应。如圆形断面的阻力系数在Re<1.4×10。5时约为1.2,而在1.4×105 对于桥梁主梁,由于具有较分明的棱角,一般认为对于类似结构,流场的分离点会被固定在棱角上,包括流场分离和再附着等特征的流场状态与雷诺数关系不大;再加上常规风洞试验中很难满足雷诺数相似的准则,因此一直以来常忽略类似结构的雷诺数效应问题。 但后续的相关研究发现,即使对于具有尖锐棱角的梯形箱梁等断面,气动力系数和斯托罗哈数对雷诺数也具有不容忽视的依赖性[13-18],而气动力系数是风荷载计算(静阵风荷载和静力稳定性)和动力分析(驰振、抖振)的基础;此外,涡激振动和颤振等现象与结构周围流场有着密切关系,雷诺数的改变如果导致流场状态的变化,也必然影响涡激振动和颤振分析的结果。目前越来越多的大跨度桥梁采用流线型箱梁,加上桥梁几何尺度的不断增大(雷诺数数值随之增大),使得雷诺数效应问题越来越突出。 目前常规风洞试验进行气动力测量的雷诺数只有几万到十几万,而对于实际大跨度桥梁,下列因素使得雷诺数数值较大: 第一,大跨度桥梁经常建在大江大河的入海口,这些区域基本风速较高; 第二,为了满足通航的要求,主梁离开水面的位置较高,加上主塔结构、斜拉索或者主缆等结构在高度方向上尺寸很大,使得设计基准风速较大,即雷诺数计算公式中的U数值较大; 第三,主梁、主塔等结构尺寸较大,即雷诺数计算公式中的D数值较大。 这些因素使得实际桥梁结构和构件的雷诺数数值较大。例如,根据年平均气象条件算得苏通长江大桥主梁的雷诺数超过1 500 万[19],超过常规风洞试验中几万到十几万雷诺数几个数量级。 利用比实际雷诺数小两个或更多数量级的模型试验测得的气动力系数和斯托罗哈数进行桥梁抗风设计和验算,可能导致设计结果偏于保守,浪费建设资金和原材料;或偏于危险,造成更为严重的后果。 对于大跨度桥梁的圆形断面构件,如斜拉桥的斜拉索、拱桥和悬索桥的吊杆、圆形桥墩或桥塔等,气动响应对雷诺数十分敏感,是研究中不可回避的问题。目前对于这些构件,JTG/T 3360-01—2018《公路桥梁抗风设计规范》[20](以下简称《规范》)中虽然考虑了雷诺数效应,但仅仅考虑了临界或超临界雷诺数状态下气动阻力与亚临界状态下的不同,并没有考虑临界雷诺数状态下横风向出现的不可忽视的升力。以高宽比为40的光滑圆形桥墩或桥塔为例,记d为圆断面直径,Ud为构件设计基准风速,则dUd对应雷诺数计算公式的分子项。《规范》规定:当dUd≥6 m2/s(高雷诺数)时,光滑圆形桥墩或桥塔阻力系数取0.6;当dUd<6 m2/s(低雷诺数)时,光滑圆形桥墩或桥塔阻力系数取1.2。而关于桥墩或桥塔的升力系数,《规范》并未做出规定。又如附加抑制风雨振气动措施(表面缠绕螺旋线等)的斜拉索,在临界或超临界雷诺数状态下升力的大小和方向,也是设计中需要考虑和研究的问题。 另外,对于其它断面形状的结构如倒角矩形的桥塔、拱桥的主拱等,由于断面尺寸大、形状不规则,都有可能存在雷诺数效应问题。 桥梁结构基本断面类型包括圆形(如桥墩、斜拉桥的斜拉索、悬索桥的主缆和吊杆、拱桥的吊杆等)、矩形(桥墩、桥塔及横梁、主梁、拱桥的主拱等)、流线型(主梁)和其它类型(如椭圆形桥塔、倒角矩形桥塔、桁架、组合类型)等。这些断面的雷诺数效应分别包括静力、流场和风致振动方面。下面分别阐述相关问题的研究进展。 圆形是在桥墩、斜拉索、主缆、吊杆等桥梁结构上常出现的断面形式,是工程中最基本的结构之一,其雷诺数效应最为复杂,研究也有悠久的历史。 分析结构周围的流场随雷诺数的变化规律可以从本质上更好的掌握结构的气动特性随雷诺数变化的规律。 20世纪中期,Roshko[21]研究了圆柱表面风压分布,试验表明当Re=1.1×105时,边界层的分离是层流分离;当Re=8.4×106时,边界层的分离变为湍流分离。随后Achenbach[22]通过增压试验的方法,在风洞中通过提高空气密度ρ,提高了雷诺数数值,发现在亚临界雷诺数区,分离点与前驻点的夹角为95°,当Re=3.0×105时,该夹角变为140°;当流场从亚临界到临界过渡时,产生非对称的分离气泡,当Re=1.5×106时,分离气泡消失。Higuchi等[23]研究圆柱流场发现:当Re>1.5×105时,伴随着旋涡脱落的减弱,非对称的分离气泡开始出现。 总结既有的研究成果,可以得到流场随雷诺数的变化规律如下: 在亚临界区,圆柱的分离点与前驻点的夹角约在75°附近;在临界区,边界层发生分离和再附着,形成非对称的分离气泡,分离点向后移;在超临界区,分离点前移,保持在120°附近;在跨临界区,分离点基本固定不变。 伴随着流场的变化,旋涡脱落的无量纲频率即斯托罗哈数也发生变化。早在1878年,Strouhal[24]通过试验发现当流体绕过圆柱体后,在尾流中将出现交替脱落的旋涡,并且旋涡的脱落频率f、流速U和圆柱直径D之间有一定的关系,之后用St=fD/U来表示旋涡脱落的无量纲频率。Von Karman研究了圆柱绕流的机理,认为两行涡街的行距等于相邻涡距的0.28倍时,涡街才是稳定的[25]。 研究发现雷诺数是影响斯托罗哈数的主要因素之一。Ribner等[26]在亚临界区范围内(1.0×104 Roshko、Schewe等[28-31]对圆柱体流场的旋涡脱落研究发现:当雷诺数在40 图1 斯托罗哈数随雷诺数的变化规律Fig.1 Strouhal number changes with Reynolds number 为了方便计算,小西一郎[32]给出了斯托罗哈数的近似公式 (4) 式中,CD为阻力系数。 圆形断面雷诺数效应的研究源于其阻力系数的研究。1912年,Von Karman研究了圆柱绕流的涡脱迹线[33]。随后Wieselsberger通过改变圆柱直径的方法,在Re为400~8×106内测量了其阻力系数随雷诺数的变化情况,发现阻力系数由Re=400时的CD=4.0减小为Re=5×106时的CD=0.3[34]。Roshko通过增压的方法对圆柱体实现了在106~107雷诺数范围内的测试试验,发现在3.5×106之前的雷诺数范围内,CD从0.3逐渐增大到0.7左右,在雷诺数达到3.5×106之后CD基本不再变化;Schewe在1.0×104kPa的增压风洞中对圆柱体进行了测力试验,发现在3.5×105~1.0×106雷诺数范围内CD保持在0.22附近,在雷诺数达到1.0×106之后阻力系数逐渐增长并稳定在0.52附近。 Simiu[35]总结了气动力随雷诺数的变化规律如下:对于光滑表面的圆柱,在低湍流度下,在亚临界区CD基本保持不变,约为1.2;在临界区阻力系数急剧下降,最低可达0.2左右(最小值跟表面的光滑程度有关),此种现象称为“Drag Crisis”;在超临界区阻力系数从0.5左右开始缓慢增大,直至高超临界区保持不变。阻力系数CD的变化如图2所示。 图2 阻力系数随雷诺数的变化Fig.2 Drag coefficient changes with Reynolds number 表面粗糙度和湍流度的变化会导致雷诺数效应的变化。刘庆宽等[36]对圆形断面光滑斜拉索模型进行了不同湍流度下的风洞试验,发现湍流度越大,圆形断面的临界雷诺数区提前越多。 Fage等[37]经过研究发现:随着圆柱表面粗糙度增加,临界区间内最小阻力系数值会增大,高雷诺数区间的阻力系数也会增大,并且高雷诺数特性向低雷诺数区域进行平移。Achenbach[38]在4×104~3×106雷诺数范围内研究了表面粗糙度对圆柱雷诺数效应的影响。试验发现,随着圆柱表面粗糙度的增大,临界雷诺数会减小;在跨临界区,粗糙度越高,最大阻力系数值越大。Ma等[39]通过风洞试验研究了粗糙度对圆柱气动力的影响。研究发现,在临界雷诺数区间内,粗糙度的增加会降低气动力的雷诺数效应,推测这是由于粗糙度提高增强了表面气流的湍流特性导致的。 图3是不同表面粗糙度的圆柱阻力系数随雷诺数的变化[40-43]。随着粗糙度的增大,临界区雷诺数的数值减小,阻力系数下降的程度也减小。 图3 圆柱的表面粗糙度对雷诺数的影响Fig.3 Influence of surface roughness on the Reynolds number of circular cylinder 早期关于力系数随雷诺数的变化研究中,关注阻力系数的较多,而对升力系数的关注相对较少。Almosnino等[44]在水洞中对两种直径的圆柱体进行研究,发现在临界雷诺数区域会产生较大不可忽视的升力。Szepessy等[45]经过系统研究发现,在亚临界区(8.0×103 Zdravkovich等[47]在其专著中对圆柱体的脉动升力进行了专门的研究,发现超临界区的脉动升力系数比亚临界区的要小。Norberg[48-49]在总结前人研究成果的基础上拟合了脉动升力系数随雷诺数变化的经验公式。 标准圆断面的斜拉索在生产、运输和安装过程中都可能出现损伤,导致表面出现划痕或断面不再是标准圆。损伤后的断面相较于标准圆断面,气动力特性会发生变化。刘庆宽等[50-51]针对切面模型、不同深度划痕模型、光滑模型和微椭圆断面模型进行了风洞试验,拟合出了不同模型的阻力系数随雷诺数的变化曲线,得出结论:表面损伤并不会改变斜拉索模型阻力系数随雷诺数的变化趋势,但是,划痕越深,临界区雷诺数的数值越小,超临界区的阻力系数越大;微椭圆断面斜拉索雷诺数临界区间较标准圆断面时有所变化,0°~60°风向角时前移,60°~90°风向角时后移。 Khalak等[52]研究发现,圆柱涡激振动振幅随雷诺数的变化曲线,按照雷诺数由低到高大致可分为初始分支、上分支和下分支三个部分,如图4所示。 图4 圆柱涡激振动振幅Fig.4 Vortex induced vibration amplitude of cylindrical Raghavan等[53]分别以直径为6.35 cm、7.62 cm、8.89 cm和15.24 cm的圆柱为研究对象,通过改变特征尺寸和模型自振频率,研究了在2.86×104 图5 不同雷诺数下圆柱涡激振动振幅Fig.5 Vortex induced vibration amplitude of a cylinder at different Reynolds numbers Kang等[54]使用数值模拟的手段,研究了两自由度圆柱在雷诺数1 450~10 200,5 800~40 800和13 050~91 800内的涡激振动特性,结果表明:随着雷诺数增加,顺风向和横风向的涡激振动振幅均有所增加,但圆柱的运动轨迹在形状上没有本质变化。 Martins等[55]同样用数值模拟的手段,对两自由度圆柱涡激振动特性在7.5×102 Gu等[56]使用弹性安装的刚性圆柱开展了水槽试验,分别通过改变弹簧刚度和圆柱直径的方法,研究了雷诺数对圆柱涡激振动特性的影响。研究发现,雷诺数对圆柱涡激振动振幅的影响大小,以某一临界折减风速为分界点。小于临界折减风速时,雷诺数对圆柱涡激振动振幅影响不明显;大于临界折减风速时,圆柱涡激振动振幅随雷诺数增加而增加。另外,综合考虑涡激振动振幅和频率,发现在模型振动频率等于或大于固有频率时,圆柱涡激振动振幅的雷诺数效应更加明显。 矩形断面会出现在桥墩、桥塔、主梁、拱桥的主肋等桥梁结构上。矩形结构由于具有明显的棱角,一般认为流场的分离点会被固定在棱角上,雷诺数效应不会明显;同时由于在试验中很难满足雷诺数的相似关系,因此在较长的时间内这个问题一直被忽视。但是后来的研究发现这类断面也有雷诺数效应问题。 Okajima[57]通过风洞试验研究了宽厚比分别为1,2,3和4的矩形柱在雷诺数2×102~2×104内,斯托罗哈数随雷诺数的变化规律;通过水槽试验研究了宽厚比分别为1,2和3的矩形柱在雷诺数小于300的范围内,斯托罗哈数随雷诺数的变化规律,并进行了流动可视化试验。研究发现,对于宽厚比为2和3的矩形柱,在斯托罗哈数突变的雷诺数处,流场结构发生了变化:低于该雷诺数时,会在上下表面再附着;高于该雷诺数时,不会发生再附着。 Robertson等[58-59]和Schewe等对具有小宽厚比的矩形结构表面风压分布随雷诺数变化的研究发现,气流在前棱角处分离后形成很宽的尾流,不产生再附着,但对于大宽厚比的矩形柱,分离的气流有可能会再附于结构的两个侧面,气流的再附会影响矩形结构侧面的风压分布和尾流情况,从而改变矩形结构气动特性。雷诺数的变化,有可能影响气流的再附着情况,这也是矩形断面雷诺数效应的由来。 Norberg[60]以宽厚比为1~5的矩形柱为研究对象,进行了Re=400~3.0×103内,0°~90°风攻角下的风洞试验,研究了不同宽厚比的矩形柱斯托罗哈数随雷诺数和风攻角的变化规律。研究发现,宽厚比在2~3,0°风攻角时,某些雷诺数下会有多个斯托罗哈数,可能是由于在这些雷诺数时,旋涡脱落强度较弱且不稳定导致的。Shimada等[61]发现长宽比为2.6和6的矩形断面出现斯托罗哈数突变的现象。 Tamai等[62]对3组不同尺寸的方柱做了斯托罗哈数实测研究,实测的雷诺数范围为3×104~3×106;作为对比,做了1组小尺寸方柱的风洞试验。研究发现,雷诺数越大,斯托罗哈数分布越分散;斯托罗哈数的上限随雷诺数的增加而增加,下限则基本不受雷诺数影响。 雷诺数变化导致气流再附着情况发生变化,从而引发气动力的变化。Simiu总结了矩形断面的阻力系数随长宽比的变化情况,研究发现,B/D在0~2时,阻力系数先增大再减小,2~4时结果具有一定的离散性。 Shimada等以矩形断面的长宽比为参数,研究了阻力系数和升力系数的变化情况,发现阻力系数在B/D=0.6时取得最大值。前述Tamai等[62]的试验还研究了雷诺数对方柱的阻力系数和升力系数的影响,发现阻力系数和升力系数整体都随雷诺数增大而减小。Larose等也对相关问题进行了研究,指出结果的离散性可能同湍流度和雷诺数有关。 Schewe[63]在增压风洞中进行了宽厚比为5的矩形柱测压测力试验,试验雷诺数范围4×103~4×105。试验发现:当攻角α≠0°时,三分力系数有较明显的雷诺数效应,尤其是升力系数;当α=4°时,升力系数在0.3~0.6变化,其随雷诺数的变化曲线有一个拐点;当α=6°和α=2°时,也有相似的变化曲线,但是拐点分别移动到了更低和更高的雷诺数。推测取决于雷诺数的分离泡形状是造成这些变化的原因。 在研究过程中发现将矩形断面的四个角进行倒角处理,雷诺数效应会发生变化。Scruton研究了倒圆角的方柱,当倒角半径与方柱宽之比r/b=0.021时,在雷诺数2.0×104~1.0×106内,阻力系数基本稳定在2.0左右;当r/b=0.167时,在雷诺数7.0×105附近,阻力系数突降至0.5左右;当r/b=0.333时,在雷诺数3.0×105左右阻力系数突降至0.4附近。即随着倒角半径的增大,阻力系数突降的雷诺数减小,阻力系数降幅增大,如图6所示。 图6 倒角方柱的雷诺数效应Fig.6 Reynolds number effect of chamfering square column Larose等研究发现在雷诺数3.0×105~2.5×106内,宽厚比为2的矩形断面,倒圆角率对雷诺数效应有较为明显的影响。杨群等[64]在Re=0.8×105~3.8×105内,分别测试了标准方柱和圆角率(倒角半径与方柱边长之比)分别为0.1,0.2,0.3,0.4方柱的气动特性。研究发现:圆角率为0.1的方柱脉动升力系数雷诺数效应明显;圆角率为0.2,0.3,0.4的方柱平均阻力系数、平均升力系数和斯托罗哈数在临界雷诺数附近有明显的“跳跃”现象,雷诺数效应明显。 陈海龙[65]以宽厚比为6 ∶1的矩形截面柱为研究对象,分别开展了高、中和低自振频率下的矩形柱涡激振动风洞试验,通过改变自振频率,达到改变涡激振动发生雷诺数的目的。试验发现,对于宽厚比为6 ∶1的矩形柱,改变自振频率时,涡激振动振幅随折减风速的变化趋势基本相同,起振风速和最大振幅差别很小,涡激振动雷诺数效应不明显。 商东洋[66]以大小两种尺寸,宽厚比为6 ∶1的矩形截面柱为研究对象,使用同一套弹簧悬挂系统,开展了涡激振动风洞试验,通过改变模型尺寸,达到改变涡激振动发生雷诺数的目的。试验发现,大尺寸矩形柱的涡激振动振幅远小于小尺寸矩形柱的涡激振动振幅,即宽厚比为6 ∶1的矩形柱涡激振动振幅随雷诺数增加而减小。 Chang等[67]通过风洞试验,采用改变自振频率的方式,研究了雷诺数为3.93×103~3.25×104时方柱涡激振动的雷诺数效应。研究结果表明,方柱的涡激振动振幅和涡激振动锁定区间均随着雷诺数增加而减小,起振风速随雷诺数增加而增加。 大跨度桥梁的主梁常用的断面形式有流线型箱梁、桁架梁和分离式双箱梁等,其中流线型箱梁和分离式双箱梁的实例更多一些。与矩形断面相比,流线型箱梁和分离式双箱梁能大幅减小气动阻力和提高颤振稳定性。 主跨193 m的大海带东桥(Great Belt East Bridge)西引桥的断面为梯形,宽高比为3.7,在设计阶段,通过风洞试验得到的斯托罗哈数为0.16,而实际建设过程中发生涡激振动时的数值为0.21,明显不同于风洞试验的结果[68-69]。Schewe等利用可高达100 bar的低速增压风洞对该桥主梁节段模型进行了雷诺数效应研究,绘出了斯托罗哈数随雷诺数的变化曲线,如图7所示。发现雷诺数小于8×104时,斯托罗哈数为0.18,与之前设计时的低雷诺数试验得到的0.16接近;当雷诺数大于4×105时,该数值增大到0.22,与实桥的0.21接近。利用低雷诺数(Re=1×105)和高雷诺数(Re=1.5×106)下的油膜流动显示图分析了桥梁底板气流的拓扑结构,发现尾流的拓扑结构改变有可能是引起雷诺数效应的原因,低雷诺数下边界层是层流分离,在迎风侧边缘产生很大的分离气泡,形成很宽的尾流区;而高雷诺数达到超临界区域时,边界层是层流分离并伴随着紊流再附同时分离气泡变小,尾流区明显变窄,并作出了流场拓扑变化的简图,如图8所示。 图7 大海带东桥西引桥主梁斯托罗哈数随雷诺数变化规律Fig.7 Strouhal number changes with Reynolds number for the Great Belt East Bridge west approach span 图8 大海带东桥西引桥主梁流场拓扑简图Fig.8 Simplified sketch of flow topologies for the Great Belt East Bridge west approach span Kubo等为了研究斯托罗哈数的雷诺数效应,对Ikara桥主梁断面进行了1 ∶121(Re=4×102~3×103),1 ∶36(Re=1×103~8×104)和1 ∶20(Re=3×104~3×105)不同缩尺比的模型试验,试验最大雷诺数达到Re=3×105,得到斯托罗哈数随雷诺数的变化情况并与实桥测压(Re=1.4×106)所得St=0.203做了比较,发现Re≥2×104时St≈0.2,此时模型试验的雷诺数条件符合设计要求。 金挺等[70]以苏通长江大桥为研究对象,通过节段模型风洞试验的方法,研究了流线型箱梁断面斯托罗哈数的雷诺数效应问题。试验雷诺数范围为Re=2.7×104~1.4×106,最高雷诺数与实桥仅差一个数量级,为目前国内针对流线型箱梁节段模型试验达到的最大雷诺数,能近似反映实桥流场情况。研究拟合出了不同风攻角下,斯托罗哈数随雷诺数的变化曲线。结果表明,在0°,±3°风攻角下,流线型箱梁断面斯托罗哈数均具有明显的雷诺数效应,在Re=2.0×105~4.0×105内,斯托罗哈数随雷诺数的变化曲线出现了明显的跃升“台阶”。 张伟等[71]使用粒子图像测速系统,获得了大海带东桥主桥的主梁断面在高低雷诺数下周围流场结构,如图9和图10所示。由图9和图10可知:在低雷诺数下,迎风侧风嘴与底板交界处出现了流动分离,导致梁底出现了贴体涡,而在高雷诺数下,梁底的贴体涡消失;主梁尾部的流场结构同样受雷诺数影响很大,随着雷诺数提高,尾部旋涡增大,并且向下游移动的更远。 图9 大海带东桥主桥梁底时均流场Fig.9 Average flow fields under bottom of Great Belt East Bridge main span bridge deck 图10 大海带东桥主桥主梁尾流时均流场Fig.10 Average flow fields of downstream of Great Belt East Bridge main girder of main span 刘健新等[72]通过测压再积分的方法得到三分力,再通过对三分力时程数据的频域分析,经计算发现刚性支撑的流线型桥梁断面在Re=6×104~1.4×105内的斯托罗哈数基本稳定在0.11,并与苏通大桥、大海带东桥西引桥和Ikara桥高雷诺数试验值(Re≥1×106)进行比较,发现虽然苏通大桥同样是流线型断面,但是因为雷诺数量级不同,斯托罗哈数相差较大。 Li等[73]研究了分离式双箱梁气动特性的雷诺数效应,试验雷诺数范围为5.85×103~1.12×105。研究表明:分离式双箱梁下表面的风压分布有明显的雷诺数效应,尤其是在前梁底板前端和后梁迎风面;前梁底板前端分离泡大小与雷诺数密切相关,随着雷诺数增加,气流在前梁底板上的再附点不断前移,分离泡逐渐减小;斯托罗哈数随着雷诺数的增加而增加,尤其是在雷诺数较低时。 德国的Schewe[74]是较早关注桥梁雷诺数效应的学者之一,他通过低速增压风洞对H形断面主梁的涡激振动问题进行试验研究时,发现高雷诺数范围内升力系数和扭矩系数的变化并不剧烈,试验的最大雷诺数达到1.25×106。虽然在试验中发现了雷诺数效应对这些断面的气动特性有一定的影响,但是并没有引起足够的重视。 Barre等对诺曼底桥进行了1 ∶10(Re=3×106~1.2×107),1 ∶50(Re=7×105)和1 ∶200(Re=2×105)缩尺比的节段模型试验。其中1 ∶10的模型试验在Re=3×106~1.2×107范围内发现阻力系数、升力系数和扭矩系数随雷诺数没有明显变化。通过对比三种缩尺模型的试验结果,发现阻力系数非常相近,在风攻角为-3°时1 ∶200试验得到的升力系数与另外两个试验最大相差0.2,扭矩系数也是只有1 ∶200的试验结果与其他稍有不同。 前述Schewe等利用低速增压风洞,对丹麦大海带东桥西引桥进行了试验研究,试验Re=3×104~4×106,阻力系数在雷诺数为5×104时达到最大值0.68,Re≤4×105时阻力系数随雷诺数增加而减小,Re=2×106时减小到0.60稳定下来;升力系数则由0.225减小到0.075左右,而后又增加至原来值再减小到最终值为0.175;扭矩系数的雷诺数效应不明显。升力系数、阻力系数及扭矩系数随雷诺数的变化曲线如图11所示。由此可知:类似桥梁箱形主梁的尖锐边缘断面细长结构会表现出明显的雷诺数效应;利用低雷诺数风洞试验得到的阻力系数偏于保守。 图11 大海带东桥西引桥主梁三分力系数随雷诺数变化规律Fig.11 Three component coefficients changes with Reynolds number of the Great Belt East Bridge main girder of west approach span Matsuda等利用加拿大NRCC的9.1 m×9.1 m风洞、日本IHI的6.0 m×3.0 m风洞和1.5 m×2.5 m风洞,对四种箱梁断面在Re=1.1×104~1.5×106内进行了气动力系数研究,比较1 ∶10(Re=1.4×105~1.5×106)、1 ∶30(Re=1×105)和1 ∶80(Re=5.1×104)几种缩尺比模型的试验结果发现,风嘴为80°角且两箱梁之间有格栅的断面三分力系数受雷诺数影响较大,升力系数和扭矩系数在风攻角大于-2°小于3°时随雷诺数增加而变化,风攻角为0°时没有表现出明显的雷诺数效应。随后Larose等总结了有尖角结构的雷诺数效应问题,指出雷诺数效应随断面形状的不同而变化。 Larose等对香港昂船洲大桥主梁的气动力系数在Re=5×105~2.5×106(以单幅箱梁宽度为特征尺寸)范围内进行了雷诺数效应研究,试验发现,在试验雷诺数范围内,阻力系数随着雷诺数增加而显著增加,在0°风攻角下变化最大,由Re=5×105时的0.045增加至Re=2.5×106时的0.065,大约增加44.44%。 李加武[75]分别针对Π型断面和流线型箱梁断面主梁缩尺模型,进行了Re=8×103~3×105的风洞试验。研究发现:流线型箱梁断面阻力系数随雷诺数增加而减小,在高雷诺数区尤其明显;Π型断面阻力系数随雷诺数增加而增大,在低雷诺数区尤其明显;流线型箱梁断面的升力系数雷诺数效应明显,而Π型断面升力系数基本没有雷诺数效应;通过增加表面粗糙度的方法可以一定程度减小三分力系数的雷诺数效应。 Li等的试验同样研究了阻力系数随雷诺数的变化关系,得出结论,在试验雷诺数范围内,阻力系数随雷诺数的增加而减小,并且前梁底板前端的分离泡长度与阻力系数近似呈线性关系,说明阻力系数的雷诺数效应与分离流的转捩有关。 Lee等[76]在韩国空军学院的中尺寸风洞中,针对缩尺比为1 ∶30的分离式双箱梁主梁节段模型进行了高速风洞试验,探究了气动力随雷诺数的变化规律,试验雷诺数范围为Re=3.0×105~2.1×106(以单幅箱梁宽度为特征尺寸)。研究发现:随着雷诺数增加,阻力系数和升力系数逐渐降低,而扭矩系数变化很小,并且存在临界雷诺数区。在临界雷诺数区间内,阻力系数和升力系数随着雷诺数增加而急剧减小,之后减小趋势放缓;栏杆的存在会减小阻力系数和升力系数的雷诺数效应。 针对主梁断面涡激振动的雷诺数效应,主要集中在梯形箱梁、分离式双箱梁、流线型箱梁和桁架梁上。 5.3.1 梯形箱梁 梯形箱梁是较早观察到主梁涡激振动雷诺数效应的主梁形式。 大海带东桥西引桥主梁采用了梯形箱梁,在建设过程中出现了涡激振动现象,风洞试验得到的涡激振动风速为23 m/s左右(Re=6.0×104),斯托罗哈数St为0.16,而实桥发生涡激振动时的风速为16~20 m/s(Re=7.5×106~9.3×106),相应的斯托罗哈数为0.21,可见雷诺数对涡激振动特性的影响不容忽视。Larose等对比多种断面形式的主梁后发现,梯形断面的箱梁气动特性对雷诺数较敏感。 5.3.2 分离式双箱梁 分离式双箱梁是一种颤振性能较好的主梁形式,但是其涡激振动性能较差。学者在研究时发现,分离式双箱梁涡激振动特性也存在着雷诺数效应。 IHI桥、昂船洲大桥和西堠门大桥的主梁都是典型的分离式双箱梁。 前述Matsuda等以日本IHI桥主梁为研究对象,开展了1:10缩尺比模型的高雷诺数风洞试验。研究发现:在±5°风攻角下,斯托罗哈数随着雷诺数增加而增大,即低雷诺数试验预测的涡激振动起振风速比实桥的要高。 导流板等附属结构对分离式双箱梁的雷诺数效应影响同样不可忽视。Larose等对昂船洲大桥主梁断面采用1:80和1:20两种缩尺比的模型进行了高低雷诺数对比试验,结果表明:导流板在低雷诺数下会增大涡激振动振幅,而在高雷诺数下能减小振幅。 张伟等[77]针对西堠门大桥,分别采用1 ∶40和1 ∶20两种缩尺比的主梁节段模型进行风洞试验,同样进行了导流板对分离式双箱梁涡激振动雷诺数效应的影响研究。发现两种雷诺数状态下涡激振动发生的阻尼比区间以及换算到实桥的振幅都不同;关于导流板对涡激振动振幅雷诺数效应的影响,得到了与Larose等相似的结论。 赖马树金[78]分别针对西堠门大桥主梁的1 ∶80(Re=6.47×103~7.93×103),1 ∶40(Re=1.17×104~1.62×104)和1:25(Re=1.87×104~2.90×104)缩尺比主梁模型进行了涡激振动风洞试验,并结合现场实测的手段,研究了分离式双箱梁涡激振动响应及其涡激振动气动力随雷诺数的变化规律。结果表明:分离式双箱梁涡激振动响应有明显的雷诺数效应,在观测的雷诺数范围内,涡激振动最大位移与雷诺数正相关;斯托罗哈数随雷诺数增加而增加,低雷诺数下涡激振动起振风速更高。 5.3.3 流线型箱梁 流线型箱梁是大跨度桥梁最常用的主梁形式,关于其涡激振动雷诺数效应的研究更丰富。 鲜荣等[79]针对南京长江四桥的流线型箱梁,利用1 ∶50和1 ∶20两种缩尺比的模型进行风洞试验发现,随着雷诺数增大,斯托罗哈数增大,涡激振动振幅减小。 崔欣等[80]利用1 ∶50和1 ∶25两种缩尺比的流线型钢箱梁主梁节段模型进行风洞试验发现:扭转涡激振动特性存在明显的雷诺数效应,随着雷诺数的增加,涡激振动振幅减小,用低雷诺数试验振幅预测实桥振幅是偏于安全的。 熊龙等[81]以某钢箱梁斜拉桥为背景,利用1 ∶50和1 ∶20两种缩尺比的主梁节段模型进行涡激振动试验,结果显示:两种模型周围流场存在明显差异,低雷诺数模型有两个涡激振动区,而高雷诺数模型仅有一个涡激振动区;低雷诺数下的涡激振动最大振幅较之高雷诺数时偏大,以低雷诺数试验振幅预测实桥振幅是偏于安全的。 董浩天等[82]以某闭口钢箱梁悬索桥为研究对象,分别开展了1 ∶122全桥气弹模型、1 ∶60主梁节段模型和1 ∶20主梁节段模型的风洞测振试验,研究发现:高雷诺数下的节段模型涡激振动锁定区间更窄,振幅更低,体现出涡激振动振幅的雷诺数效应;全桥气弹模型试验由于多构件同时参与,其涡激振动现象与节段模型有较大差异。 胡传新等[83]对缩尺比分别为1 ∶70(Re=6.08×103~2.28×104)和1 ∶20(Re=1.06×104~1.40×104)的流线型箱梁主梁节段模型进行了涡激振动风洞试验。研究表明:与小缩尺比模型相比,大缩尺比模型试验时出现了扭转涡激振动以及更高阶的竖向涡激振动;高雷诺数时的涡激振动起振风速低于低雷诺数时起振风速,高雷诺数的试验结果更为不利。 刘庆宽等[84]研究了流线型箱梁涡激振动振幅的雷诺数效应,得到与前人相似的结论:低雷诺数下的涡激振动振幅高于高雷诺数下的涡激振动振幅。李震[85]进一步研究发现,流线型箱梁涡激振动振幅与阻尼比的关系也存在雷诺数效应。 5.3.4 钢桁架梁 杨咏漪等[86]以渝利铁路韩家沱长江大桥(钢桁架斜拉桥)为背景,利用1 ∶45.77和1 ∶19.74两种缩尺比的主梁节段模型进行风洞试验,结果表明:以低雷诺数涡激振动试验结果预测的实桥振幅,高于高雷诺数试验结果预测的实桥振幅,用低雷诺数试验结果预测实桥振幅是偏于安全的;低雷诺数试验预估的起振风速高于高雷诺数试验。 上述学者对包括流线型箱梁、分离双箱梁、钝体箱梁以及桁架梁在内的多种断面形式主梁涡激振动雷诺数效应进行了研究。结果表明:同种断面形式主梁在高、低两种雷诺数状态下的涡激振动特性存在明显不同,雷诺数效应明显;不同断面形式主梁涡激振动对雷诺数的敏感性存在差异;由于因为主梁绕流形态对外形变化极其敏感,断面形状相近但细部尺寸不同的主梁涡激振动雷诺数效应也存在差异。 根据文献[77-86],对于梯形箱梁、流线型箱梁、钢桁架梁和分离式双箱梁,低雷诺数试验结果会高估实桥涡激振动振幅起振风速。参考Schewe等、金挺等、Matsuda等和赖马树金的研究,为更好反映实桥的涡激振动特性,风洞试验雷诺数应尽量控制在与实桥雷诺数相差一个数量级以内。 桥梁断面涡激振动雷诺数效应非常复杂,上述研究绝仅针对特定断面的主梁,并不具有普遍性,有必要系统而全面地研究主梁涡激振动的雷诺数效应。 虽然学者们针对桥梁风工程中的雷诺数效应问题进行了很多研究,但是由于问题的复杂性,目前仍有许多问题尚待解决。 第一,气动力和风致振动研究不全面 (1)升力系数的雷诺数效应 目前的研究中,关注阻力系数的较多,而对升力的关注程度不够。许多对称结构如圆断面结构在临界雷诺数下出现不可忽视的升力,对这种升力的大小和作用评价不足。例如刘庆宽等以南京二桥南汊桥的斜拉索为例说明了该问题,如果考虑升力的作用,在风速不大于65.0 m/s时,风荷载在风速50.5 m/s时取得极大值,也是最大值;只有风速大于65.0 m/s时,风荷载才在最大风速下取得最大值。有必要在高雷诺数下对升力系数进行全面系统的研究和评价。 (2)颤振和驰振的雷诺数效应 桥梁颤振稳定性研究和临界风速的确定方法包括经典理论方法、直接试验方法和理论与试验相结合方法[87]。其中无论是直接试验方法确定颤振临界风速还是理论与试验相结合方法确定颤振导数均涉及到雷诺数问题。而颤振临界风速与颤振导数是否随雷诺数发生变化仍未明确。 斜拉桥斜拉索、悬索桥主缆和吊杆、桥塔以及桥梁施工过程中最大悬臂结构均可能发生驰振。驰振与气动外形密切相关,即断面形状和风攻角对驰振不稳定性有重要影响,同样的气动外形在高雷诺数下的流场形态与低雷诺数状态下的结果是否一致尚未确定。 第二,缺乏对附加结构影响的系统研究 为了使桥梁结构具有更好的气动特性,在结构表面增添附加结构是常用的手段,如:为了防止风雨振,在斜拉索表面缠绕螺旋线和设置凹坑等;为更好的抑制涡激振动,在主梁上安装导流板、抑流板和稳定板等。这些措施对桥梁结构雷诺数效应的影响是复杂的,目前没有一般规律性的结论,还有待开展系统性的研究。 第三,缺少实桥雷诺数下的结果 为了获得实桥雷诺数下的结果,现场实测是一种可行的方法。但是由于受到风的参数、现场情况和传感器的限制,实测常遇到诸多难题,导致实测结果匮乏。 首先是捕捉到较大的风速比较困难。现在的大桥设计都是基于百年一遇的风速,而针对雷诺数的实测只能选在建设期内的某一段时间(桥面铺装和通车会影响桥面压力测试),在短时间内遇到很高风速的概率很小,如陶奇等[88]从2007年5月—2007年8月进行的三个月实测,捕捉到的最大风速仅为12.3 m/s;其次是风向不可控制,来流风向大都与主梁存在一定的水平和竖直偏角;再次,实测只能通过数量有限的测压点测试主梁的表面压力,再通过压力积分得到气动力,不得不忽略风与桥梁表面的摩擦力,另外压力测试的准确程度依赖于测压点的数量、分布密度和现场传感器的精度,桥上的细部结构如栏杆、隔离带、检修结构等由于不方便布置测点,其作用经常被忽略。 第四,试验方法的局限 由公式Re=UD/ν分析如何提高风洞试验中的雷诺数。要提高雷诺数,或是提高来流风速(增大U),或是增大结构的特征尺寸(增大D),或是减小运动粘性系数(减小ν)。由于风速过高会引发其它的空气动力学问题(如空气的压缩性问题和马赫数不一致带来的问题等),因此获得高雷诺数的方法主要通过增大D和减小ν来实现。与此对应,目前世界上低速高雷诺数风洞主要有三种类型[89]:第一类是常压运行的全尺寸风洞(增大D),如美国NASA于1982年改造完成的36 m×24 m风洞;第二类是低温风洞(减小ν),如德国DLR于1984年建成的KKK风洞;第三类是增压风洞(减小ν),如英国RAE于1978年建成的5 m增压风洞。此外还有采用重气体(如氟利昂,减小ν)的方法。 对于进行桥梁风工程研究的风洞而言,提高雷诺数都有一定的难度。对于进行全桥模型试验的风洞,虽然具有较大的宽度,但是由于全桥气弹模型的风速缩尺为几何缩尺开方分之一,因此这类风洞的最大风速经常在20 m/s以内,而其他如增压、低温和利用高密度气体等方法一般也不实用,且成本高昂。因此,如何经济实用的获得更高的试验雷诺数,仍是一个有待解决的问题。 第五,抑制手段的缺乏 由于在风洞试验中模拟实际雷诺数有难度,而增大结构表面粗糙度和来流湍流度,可在相对较低的雷诺数下得到与临界或超临界雷诺数状态下相似的平均阻力特性,因此受雷诺数效应影响较大的圆形截面结构,如冷却塔和电视塔[90-91]等,在风洞试验中通常采用在模型表面粘贴绊线等增大表面粗糙度以及提高来流湍流度的方法。但是这种方法会明显减小圆形截面结构的平均升力系数。 对于矩形截面结构和主梁结构的气动力,使用增加表面粗糙度和来流湍流度的方法,对雷诺数效应的抑制效果有限,甚至在某些情况下会放大雷诺数效应。 如何抑制风洞试验中的雷诺数效应,通过低雷诺数风洞试验获得桥梁结构实际雷诺数下的气动力、流场和振动特性,目前依然是一个未能很好解决的问题。 随着桥梁跨度和结构尺度的增大,桥梁结构的雷诺数效应问题愈发引起关注。为了解决相关问题,给出如下建议: (1)一些特种风洞可以通过调整影响雷诺数的相关参数实现相对高的雷诺数,建议开展特种风洞模型试验研究。 (2)大尺度模型实测能够获得模型在高雷诺数状态下的气动特性,建议开展大尺度模型的实测工作。 (3)随着计算机性能的飞速提高及流体力学的不断发展,CFD数值计算将是雷诺数效应研究的非常有前途的技术手段。 (4)深入研究粗糙度和来流湍流度对桥梁断面雷诺数效应的影响规律和机理,为在低速风洞中模拟高雷诺数下流动状态提供量化参数。 (5)利用机器学习方法,对风洞试验和现场实测数据进行训练,建立桥梁各种断面的气动特性在全雷诺数范围内的预测模型,一定程度上可以预测实际桥梁的气动特性。3 圆形断面的雷诺数效应研究
3.1 流场随雷诺数的变化
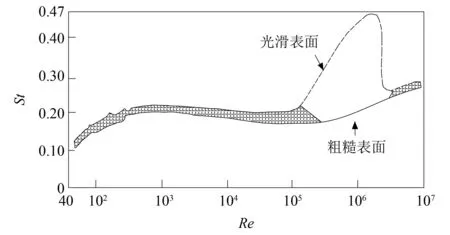
3.2 气动力随雷诺数的变化

3.3 涡激振动随雷诺数的变化
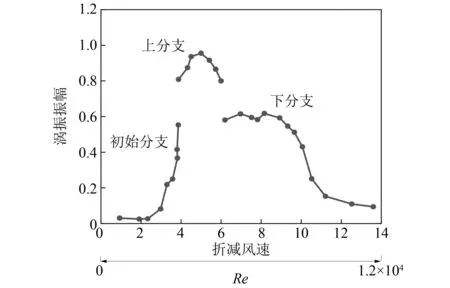

4 矩形断面的雷诺数效应研究
4.1 流场随雷诺数的变化
4.2 气动力随雷诺数的变化

4.3 涡激振动随雷诺数的变化
5 主梁断面的雷诺数效应研究
5.1 流场随雷诺数的变化
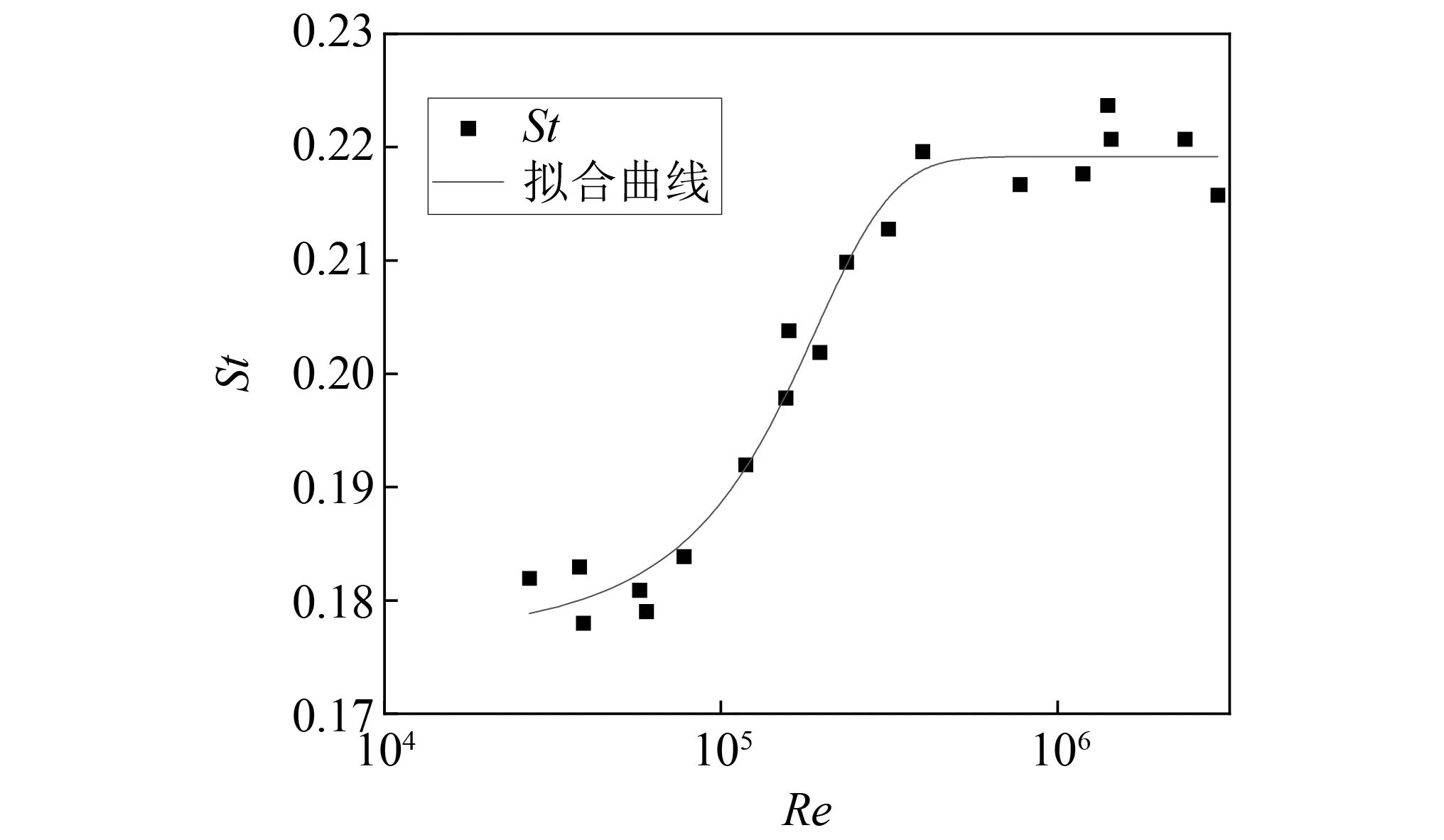


5.2 气动力随雷诺数的变化
5.3 涡激振动随雷诺数的变化
6 尚待解决的问题
7 结 论

