大型矿用齿轮传动系统宏观参数动力学优化

杨孝新, 肖 鹿, 杨晓东, 李奇奇, 高晓鑫, 金鹏程

(1.中国矿业大学 矿业学院 江苏 徐州 221116;2.新疆天池能源有限责任公司,新疆 昌吉 831100; 3.新疆维吾尔自治区科技发展战略研究院,乌鲁木齐 830000;4.新疆大学 机械工程学院,乌鲁木齐 830017)

现代工业生产中,机械设备向着大型、复杂、自动化方面发展。大型矿用齿轮传动系统由于系统复杂,工作环境恶劣,故障发生率很高,且一旦发生故障直接影响企业的经济效益,因此,为避免传动系统发生故障,提高系统可靠性,需要在动力学特性上对系统进行更完备的设计。传统的设计方法过程复杂,且常依赖经验,为提高设计的效率、系统性与完备性,在大型矿用齿轮组设计的初始阶段,有必要对矿用齿轮传动系统进行多目标宏观参数的优化。

针对大型矿用传动系统的宏观参数的动力学优化,国内外学者分别从动力学模型的建立与优化模型的设计中进行了大量研究。王勇等[1]利用集中质量法对单对直齿轮进行动力学建模,借助遗传算法优化了齿轮对的随机振动与质量,张庆伟等[2]建立了大型矿用齿轮系统的集中参数模型,利用混合离散变量组合型法同时优化了振动加速度与系统质量,减少了制造成本,提高了可靠性。综上,在以往对齿轮系统优化的研究中,大多建立集中质量法模型,将轴、轴承,齿轮视作含有阻尼的弹性质量块,无法预测齿轮在轴上不同位置的动态响应,导致无法对平行轴齿轮系统进行考虑布局参数的动力学优化。为此,Neriya等[3]首先将轴的质量与刚度离散化,并针对齿轮转子系统进行了动力学的响应分析;Kuber等[4]建立了多级轴系与多啮合齿轮系统的耦合动力学模型,对级间相位角对轴承动载荷的影响进行了分析;常乐浩等[5]借助广义有限元方法,建立了定轴齿轮系统与箱体的通用建模方法,并证明了该方法的有效性与求解响应时的精确性。

为降低齿轮系统的振动与噪声,以往的齿轮系统宏观参数的优化模型建立时,其目标函数大多为增大齿轮重合度或直接以噪声经验公式为目标函数,付学中等[6]针对斜齿轮振动噪声问题,以斜齿轮啮合刚度波动幅值为目标函数,采用轮齿承载接触分析(loaded contact analysis tooth,LTCA)与遗传算法对斜齿轮进行了修形优化。蔡文奇等[7-8]以某电动汽车两档变速箱传动系统为对象,以渐开线斜齿轮总重合度最大为优化目标,对变速器齿轮副进行了宏观参数优化,并进一步进行了修形研究。蒋春明[9]为提高变速器可靠性以重合度与传动系统体积为目标函数对三轴四档汽车变速器进行了多目标优化;邵正宇等[10]以噪声经验公式与齿轮体积为优化目标函数对准双曲面齿轮的设计参数进行了优化。此类目标函数虽然可以减少齿轮系统的刚度激励,但未考虑复杂系统与转速的频率关系,因此可能减弱优化效果。对于考虑频率关系的齿轮系统的动态优化,目标函数表达式常由各项参数与动力学微分方程组求得的动态响应拟合而成,过程相对复杂,其研究成果相对较少。如秦大同等[11]采用谐波平衡法求解大型矿用传动系统的动态响应,以振动加速度为目标函数进行优化;聂慧阳[12]针对两路分流齿轮传动系统建立集中参数模型,在求解动态响应的基础上分析了均载系数并予以优化。

上述研究大多使用集中质量法建立动力学模型,无法预测齿轮在轴上不同安装位置的动态响应且对不同目标函数对系统动态特性的影响分析较少,齿轮副的动态啮合力幅值作为引起齿轮系统啸叫问题的主要激励源,传动系统的体积作为系统经济性的体现,两者在设计中常常是相悖的,为针对此类不足,有必要建立综合动力学模型并进行多目标寻优。本文以大型矿用齿轮箱中的定轴传动系统部分为研究对象,利用广义有限元法建立宏观参数化的动力学模型,基于NSGA-Ⅱ优化算法建立包含不同目标函数的优化模型并对其所求动态响应进行对比分析。

1 二级齿轮传动参数化动力学模型建立

如图1所示,二级大型矿用齿轮传动系统由输入轴、中间轴、输出轴、两级齿轮与三对轴承组成。以大型矿用齿轮箱中的二级定轴传动系统为研究对象,将其离散化,建立各单元参数化动力学模型,再将各单元动力学按照不同安装方式实现参数化组装,以实现传动系统参数与动态响应的一一映射,其映射关系可为优化的目标函数拟合提供数据集。

图1 二级齿轮传动系统结构图Fig.1 Structure diagram of secondary gear transmission system

1.1 轴的参数化建模

如图2所示,建立8自由度铁木辛柯梁动力学模型,其质量与刚度子矩阵可参考文献[13]。将子矩阵按节点叠加形成轴的总体刚度矩阵。因此,由式(1)所示,在确定材料属性前提下,其总体刚度矩阵可利用轴的轴径参数与轴长参数表示

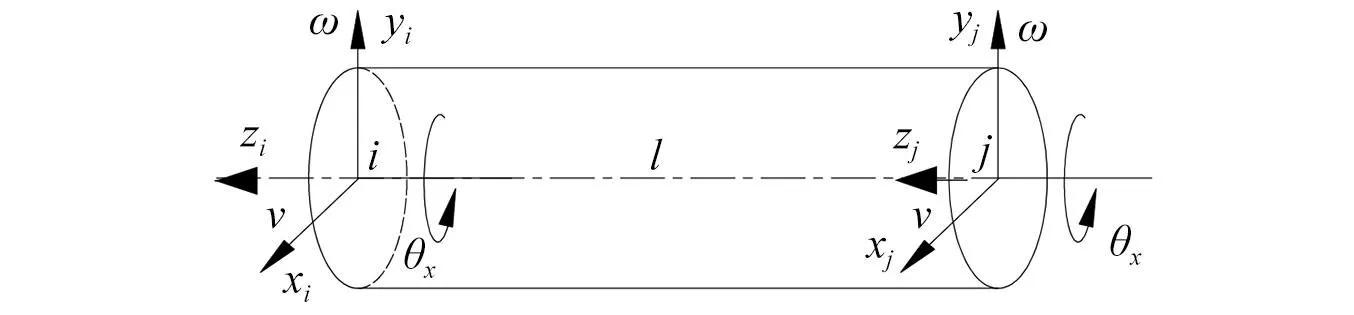
图2 轴段单元定义Fig.2 Shaft segment unit definition

Ks=f(ri,n)

(1)

式中:ri为轴半径,i=1,2,3;n为轴长参数,代表将轴离散单元数量,为计算结果的精确性,将轴段单元设为0.05 m。

1.2 斜齿轮的参数化建模

如图3所示,建立八自由度斜齿轮啮合模型,根据达朗贝尔原理建立微分方程组即公式,整理得到8×8啮合单元刚度矩阵

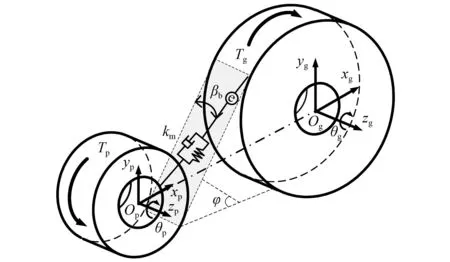
图3 斜齿轮啮合单元Fig.3 Helical gear meshing unit

(2)

式中:mp/g为主、从动齿轮质量;Izp/zg为主、从动轮绕z轴的转动惯量;cm为啮合阻尼;km为综合啮合刚度;βb为齿轮螺旋角;φ为齿轮压力角

其时变啮合刚度km采用势能法求解

(3)

各参数详见参考文献[14],利用上述4种势能分别计算赫兹刚度kh,弯曲刚度kb,剪切刚度ks与径向压缩刚度ka,同时考虑齿轮基圆的柔性变形,计算所对应刚度

(4)

式中参数要取决于齿数,次要取决于刀刃半径、压力角与齿顶高,具体计算为在实际范围内对式中系数进行多项式拟合计算得出,具体方法可参考文献[15]。因此刚度为

(5)

将刚度矩阵形成函数程序,输出的啮合刚度矩阵可利用函数表示为

kv=f(zi,mi,Li,α,βb)

(6)

式中:zi为两级齿轮齿数;mi为两级齿轮模数;Li为两级齿轮齿宽;α为压力角;βb为两级齿轮螺旋角

1.3 轴承的动力学模型

对轴承而言,在轴的转动过程中其刚度由于滚子数目奇偶的变化而往复变化。对奇压而言,其刚度为轴承所受径向载荷与径向位移间的比值,同时借由滚子方位角计算出偶压刚度,本文中利用正弦曲线近似轴承径向时变刚度,对轴向进行全约束,如图4所示。

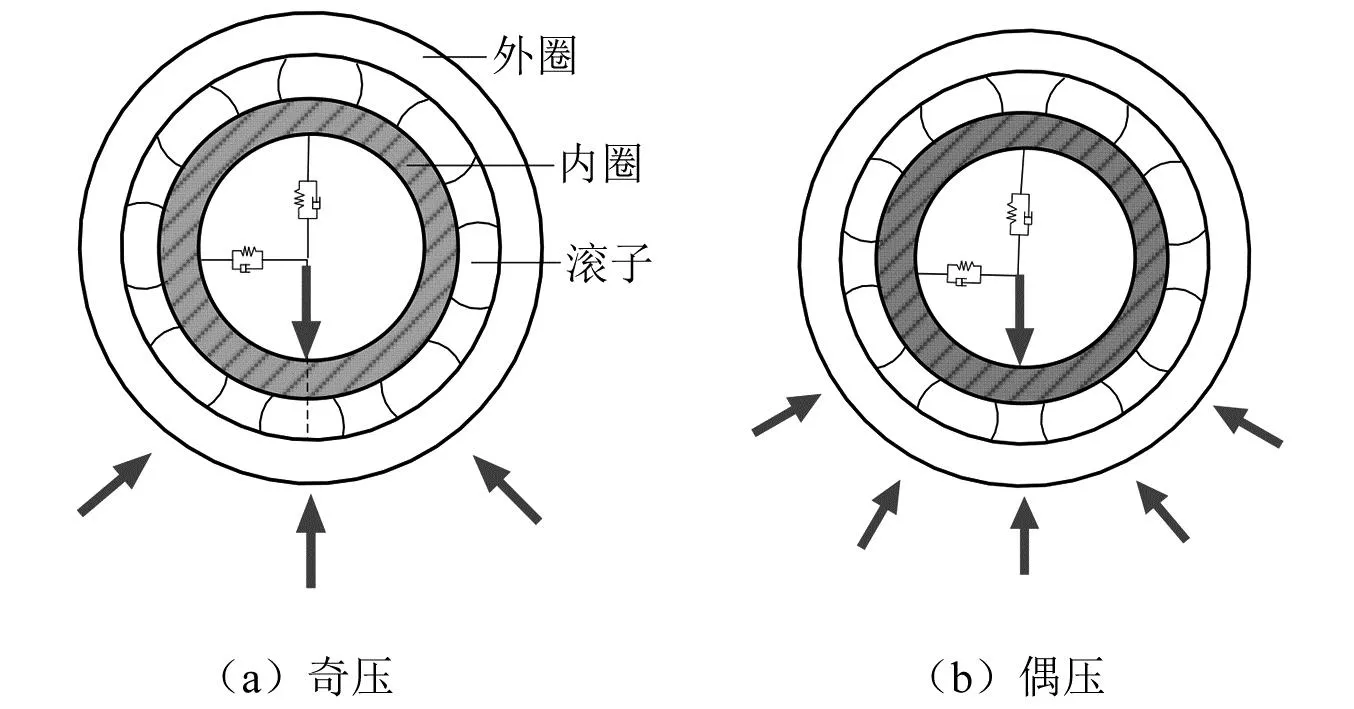
图4 轴承动力学模型Fig.4 Dynamic model of bearing

(7)

Kx,y(t)=K0+Kasin(2πfbt+β0)

(8)

式中:Kx,y(t)为水平与垂直方向的轴承时变啮合刚度;K0为轴承静刚度,K0=(kbe+kb0)/2;Ka为轴承刚度波动幅值;fb为通过频率;β0为初始相位角。

1.4 齿侧间隙

当轮齿存在间隙时,齿轮运转过程振动较大或小扭矩时会产生脱啮现象,为探究轮齿脱啮对优化结果的影响,本文采用分段函数表征齿侧间隙与齿轮副沿着啮合线方向上的相对位移之间的关系。

(9)

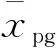
1.5 参数化定轴传动系统动力学模型

根据1.3节动力学模型的分析,可将任意定轴传动系统按照节点进行刚度矩阵组装,如图5所示。因此任一定轴传动系统总刚度矩阵可以函数表示

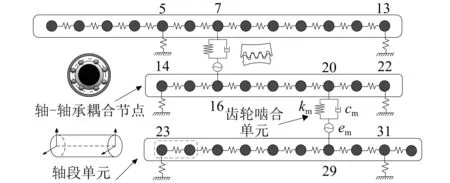
图5 大型矿用传动系统有限元模型Fig.5 Finite element model of large mine transmission system

K=f(ri,zi,mi,Li,α,βb,n,n1,n2)

(10)

式中:n1为第一级齿轮安装参数;n2为第二级齿轮安装参数;定义齿轮安装参数距中间轴端部节点数目,n1/2=1,2,3,…,(n/2-1)。

如图6所示。施加边界条件后,消除刚体位移的影响,得总体刚度矩阵。总装后含齿轮系统的整体动力学微分方程为

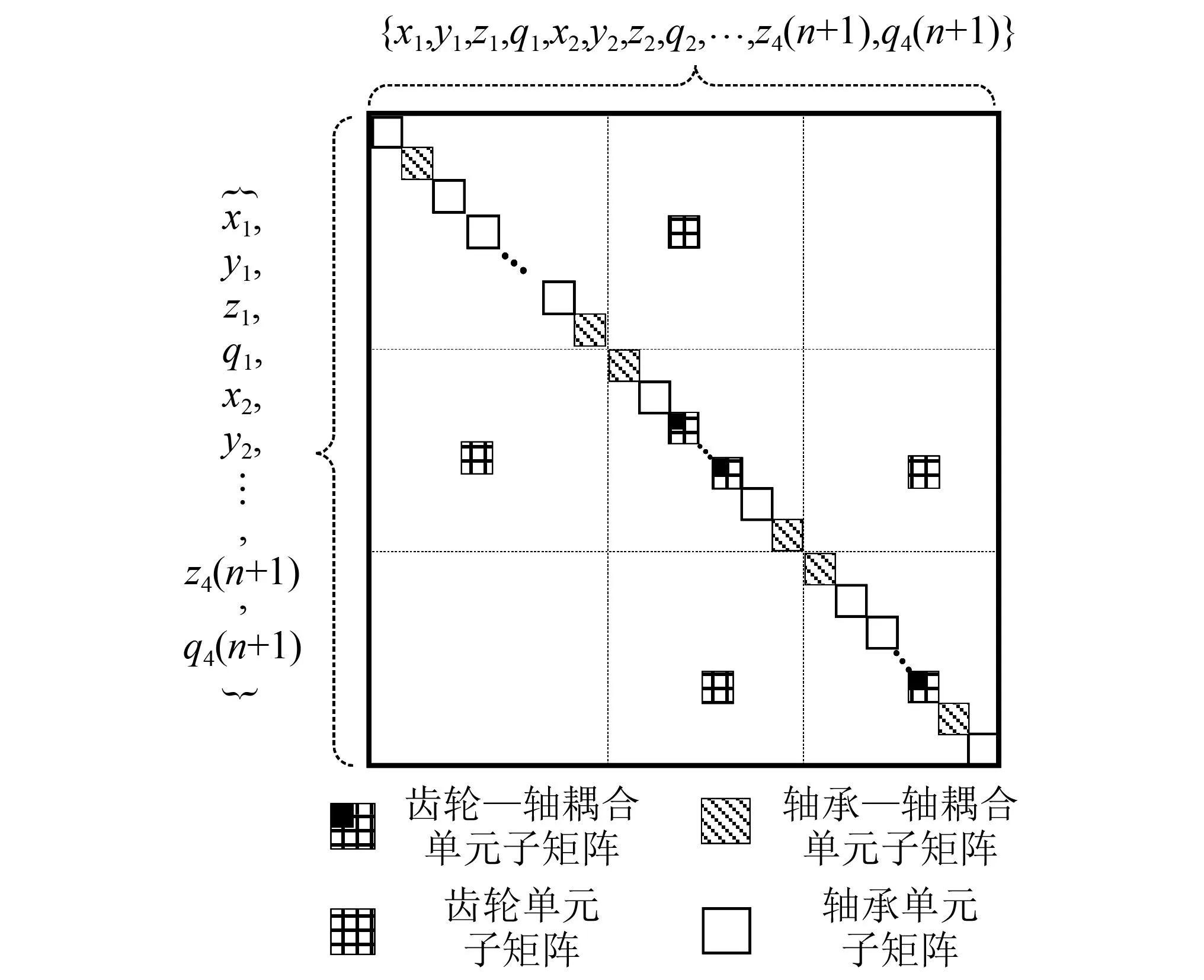
图6 大型矿用传动系统整体刚度组装示意图Fig.6 Schematic diagram of overall rigidity assembly of large mining transmission system

(11)

式中:X为节点位移列阵为{x1,y1,z1,θ1,x2,y2,z2,θ2,…,x4(n+1),y4(n+1),z4(n+1),θ4(n+1)};M,C,Kf分别为含质量总装矩阵、阻尼总装矩阵及刚度总装矩阵;Po为系统外部激励;Fe为系统误差激励。

由上述分析可知,整体动力学的刚度矩阵为各项宏观参数的函数,因此经过数值计算求得的系统动态响应为相同参数的函数,本文所用建模方法的正确性已于文献[16]中进行试验验证,因此不再赘述。

2 宏观参数优化模型

为改善大型矿用传动系统的噪声特性与质量,目标函数的设定与优化策略的制定,优化算法的选择一直未形成系统性的规范,本文以齿轮重合度与数值计算后求解所得齿轮啮合力均方根值与包含轴系的传动系统质量为不同的目标函数,综合设计优化模型与智能算法。

2.1 目标函数

2.1.1 重合度目标函数(F1(x))

重合度作为影响衡量齿轮承载能力与传动平稳性的重要指标,针对齿轮传动系统的动态特性,齿轮重合度越大传动越平稳,振动噪声越小。对渐开线斜齿轮而言,其总重合度ε为端面重合度与轴向重合度的叠加

ε=εα+εβ

(12)

端面重合度与轴向重合度计算如下

(13)

(14)

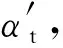
(15)

定义总重合度的相反数最小为第一目标函数

f1=min(-ε)

(16)

2.1.2 动态特性最优目标函数(F2(x))

对于矿用齿轮箱而言,轴承加速度连接箱体,对其传动平稳性与系统结构噪声具有重要影响,因此,可以将轴承加速度均方根值作为动态性能最优目标函数可以写为

(17)

式中:nm为啮合齿轮对个数;Fi为第i级啮合的动态啮合力。

2.1.3 质量目标函数(F3(x))

齿轮系统需在满足强度与动态特性的要求的基础上尽量减小体积与质量。对于二级大型矿用传动系统而言其质量为轴,齿轮与壳体质量的叠加,由于本文只考虑传动系统因此忽略壳体质量,传动系统质量可表示为

(18)

式中,Li为输入轴、中间轴、输出轴长度。

2.2 设计变量

据建模过程分析可知,可将影响系统动力学刚度矩阵的各项宏观参数作为优化设计变量

X=[zjmBr1r2r3nn1n2αβi]T

(19)

2.3 约束条件

2.3.1 齿数约束条件

为避免干涉,二级传动从动轮与输出轴的距离需大于一定值

(20)

式中:r1为输入轴半径Zp1/2为一级或二级主动轮齿数;Zg1/2为一级或二级从动轮齿数;m为模数;α为相位角;ξ为一个基于安全性考虑的小量,本文取5 mm。

2.3.2 轴径强度约束

(21)

式中:C为与轴材料有关的系数;vs为传动轴的转速;P为轴传递的功率;di为第i根轴的直径。

2.3.3 传动比约束

二级传动系统传动比一般为8～40,考虑到优化后齿数的变化会导致总传动比的变化,需要对总传动比进行约束

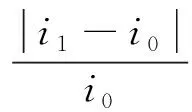
(22)

式中,i0,i1分别为优化前、后传动比。

2.3.4 强度约束条件

强度约束包括齿轮副的齿面接触疲劳强度与齿根弯曲疲劳强度与轴的扭转强度。

(23)

(24)

(25)

2.4 算法选择

由于本文优化问题基于Newmark-β实时演算得到的数值解集具有强非线性,因此无法利用与梯度有关的优化算法进行寻优,群优化算法作为一种使用群体的随机搜索算法为此类问题提供了思路[18]。NSGA-Ⅱ同时考虑了拥挤度与精英策略,利用拥挤度比较算子,降低了计算复杂度,有效避免了优化过程中的局部收敛[19]。

本文采用带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)对整个二级传动系统宏观参数进行寻优,如图7所示,基于Pareto理论,各项目标函数无须设置贡献度,如图7所示,优化结果为一个非劣解集。

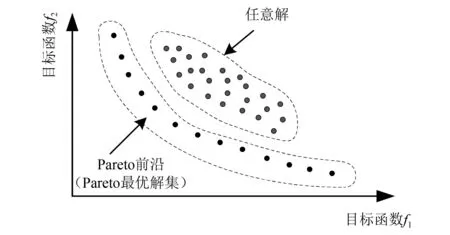
图7 Pareto平面示意图Fig.7 Pareto plane

首先需对设计变量进行编码,其方式取决于优化变量的个数与特征。就本文而言,设计变量包含齿数、齿轮组安装位置等整型变量与轴径、齿宽等浮点型变量,采用二进制编码方法会导致搜索空间维度过高对最优解的求解形成困难,因此本文采用整型与浮点型混合编码的方式对设计变量进行编码优化,具体参数设置如表1所示。

表1 遗传算法参数设置Tab.1 Genetic algorithm parameter setting

3 算例优化结果

为验证本文所提出的优化模型的有效性,以某公司大型矿用齿轮箱为例进行宏观参数多目标寻优,为方便计算,选用减速器额定转速为500 r/min,负载扭矩为2 000 N·m,传动系统与轮齿宏观参数如表2所示。

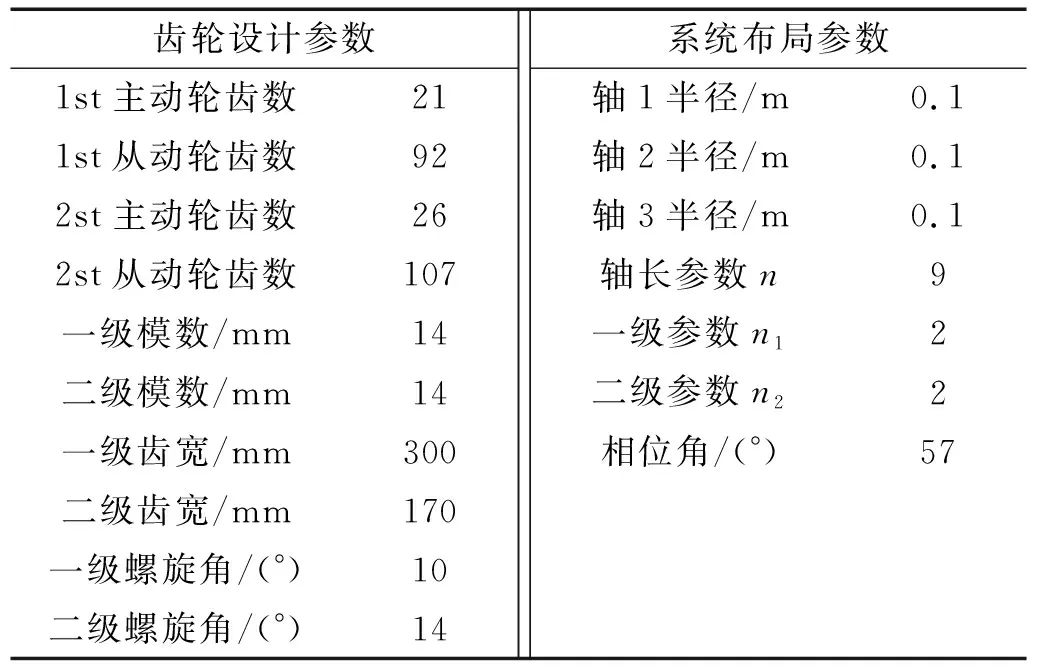
表2 传动系统宏观参数Tab.2 Macro parameters of transmission system

为分析多目标优化结果的宏观参数特征与动态特性,以B2优化策略为例,如图8所示,可见经多目标优化后,轴系布局更紧凑,加工制造也更经济。

图8 优化前、后系统布局对比Fig.8 Comparison of system layout before and after optimization

为验证优化的有效性,将初始参数与优化后的参数代入编写的MATLAB程序中,首先不考虑传动系统质量,以重合度与轴承加速度均方根值作为目标函数进行优化,优化结果为表中A1。由优化结果分析得知虽然齿轮动载荷均方根值得到有效减少,但系统质量大幅增加,因此基于重合度或轴承加速度均方根值的优化适用于高扭矩,体积不受限的设计中。二级齿轮系统的体积优化是大型矿用装备设计中的一项重要环节,因此将加速度均方根值与系统质量作为目标函数同时优化,得到Pareto平面如图9所示,在优化后得到的Pareto平面内选取三种典型优化策略B1～B3,如表3所示,将三种优化策略优化参数代入本文所建动力学模型中得到轴承加速度均方根,与初始参数所求结果进行对比,如果如表4所示。

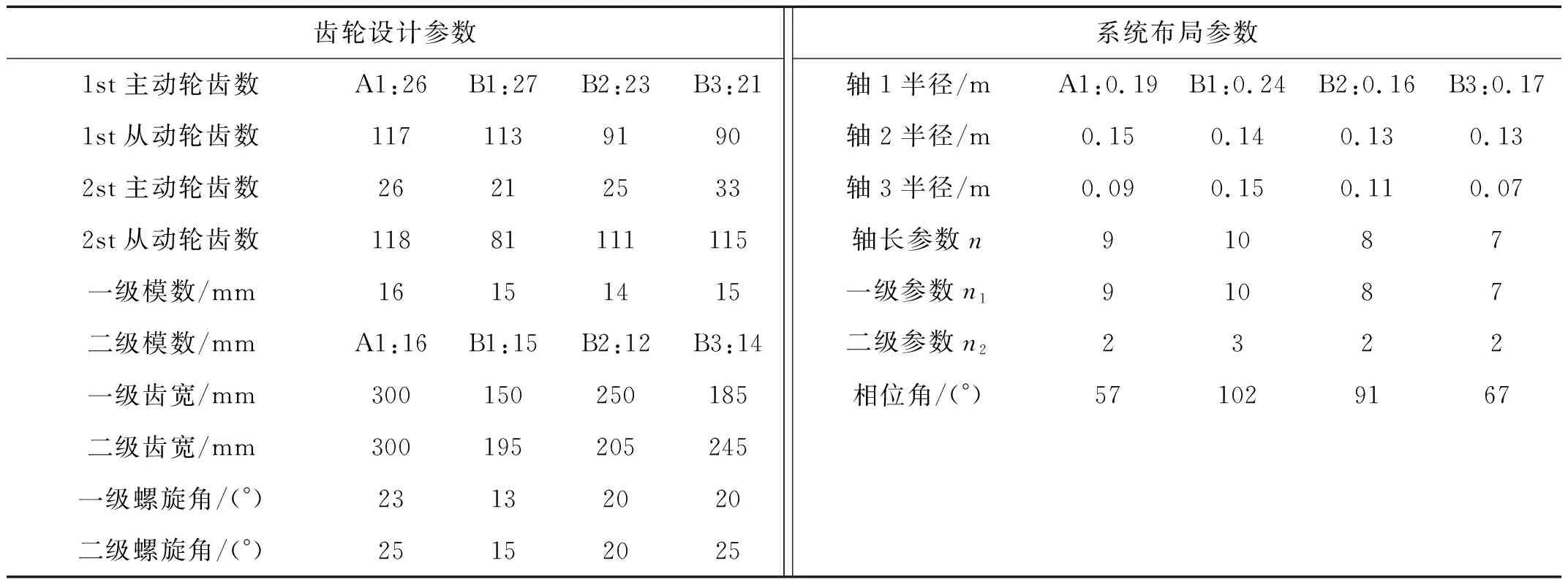
表3 不同目标函数优化方案系统参数Tab.3 System parameters of different objective function optimization schemes

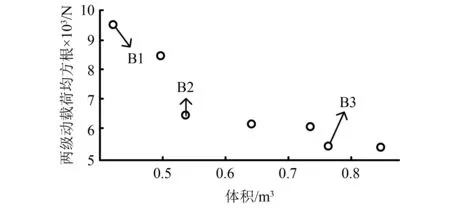
图9 Pareto平面Fig.9 Pareto plane

表4 不同方案优化目标值Tab.4 Optimization results of different schemes

4 优化参数验证

选取策略B2的各项参数代入编写的程序中,得到第一级、第二级齿轮动态啮合力的时域响应,傅里叶变换后得到其频域信号,将其与优化前的响应对比分析。优化前的第一级齿轮啮合频率为

(26)

二级齿轮啮合频率为

(27)

如图10所示,优化后的一级齿轮啮合力幅值明显降低,具体为优化后幅值为2 557 N,优化前的动态啮合力幅值为2 770 N,降低7.6%。由频域图可见,振动响应的主要频率成分为一级齿轮啮合频率及其倍频,由于优化前后一级齿轮啮合频率较为相近,因此在低阶频率成分将近重合,到高倍频处逐渐拉开差距,大部分频率成分的能量均有所低。由图11所示,优化后的二级齿轮啮合力幅值小幅度降低,具体为优化后幅值为19 537 N,优化前的动态啮合力幅值为23 107 N,降低15.7%。由频域图可见,振动响应的主要频率成分为二级齿轮啮合频率与倍频,二倍啮合频率与三倍啮合频率成分有小幅增加,其原因在于该频率接近系统某一固有频率,因此,当设计中对某阶频率成分有要求时,可通过改变优化目标函数进行频域级的精细化设计。

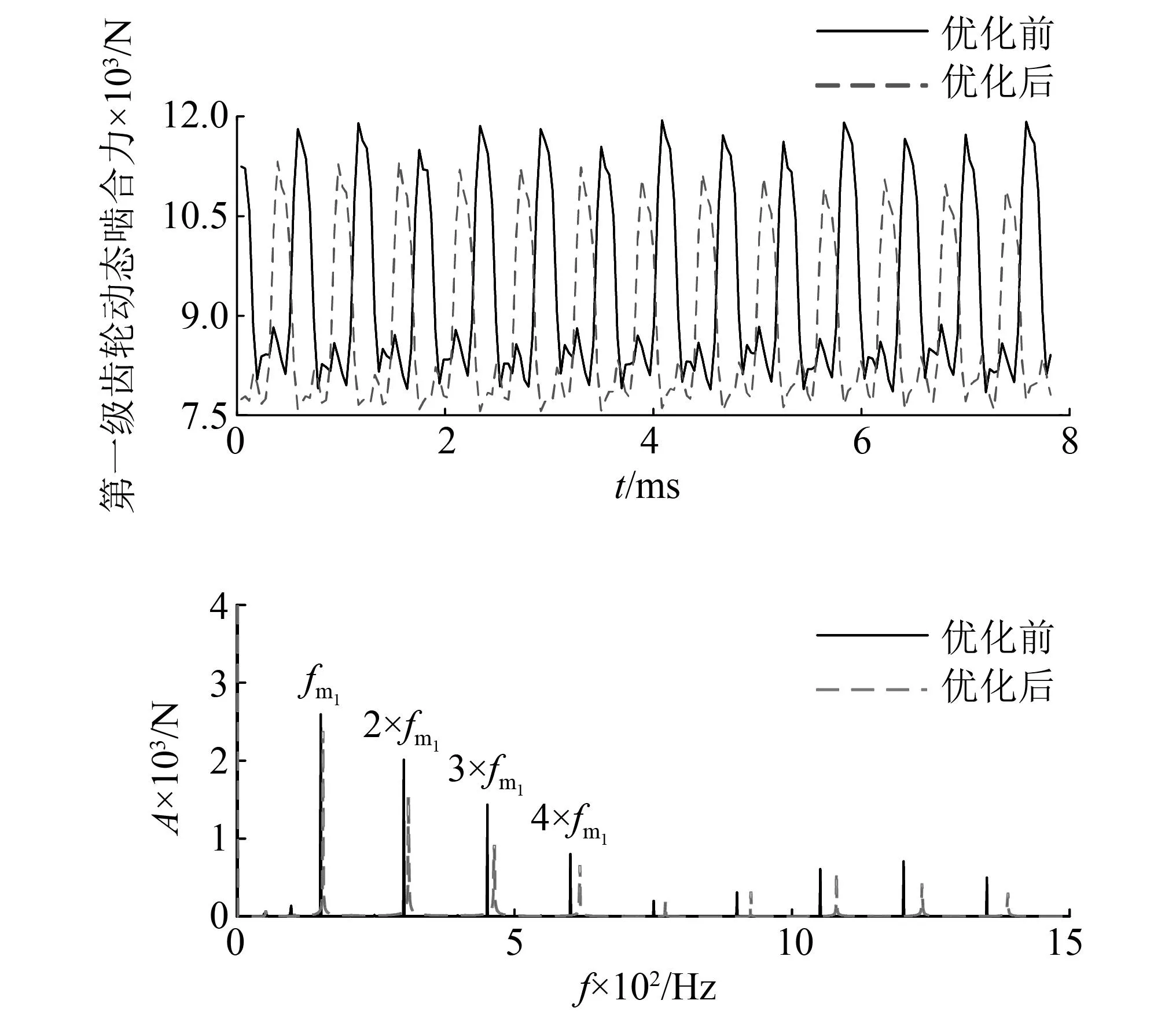
图10 第一级齿轮动态啮合力时域与频域图Fig.10 Time domain and frequency domain diagram of the dynamic meshing force of the first stage gear

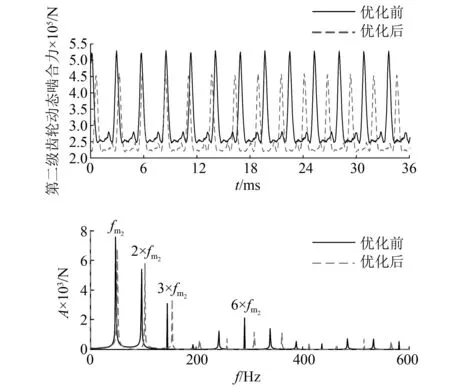
图11 第二级齿轮动态啮合力时域与频域图Fig.11 Time domain and frequency domain diagram of the dynamic meshing force of the second stage gear

将考虑偏心的优化结果代入动力学程序中,得到优化前、后的齿轮动态啮合力,如图12和图13所示,当考虑偏心时,轮齿会发生脱齿行为,整个啮合过程经过接触、分离、再接触的一个反复过程,由图可见,优化前齿轮动态啮合力幅值为2 942.94 N,优化后幅值降为2 589.02 N,降幅为12%,由此可见,本文方法以处理过的实时计算的数据集为目标函数,可适用于考虑多源时变激励的齿轮传动系统。另外,优化前齿轮动态啮合力均值为1196.63N,优化后为965.21 N,其啮合力均值的变化原因为:经优化,齿轮齿数发生了变化,导致静平衡力发生了变化。实际应用中,应当根据各级齿轮强度进行配齿设计,以免降低齿轮疲劳寿命。

图12 考虑偏心的齿轮动态啮合力(优化前)Fig.12 Dynamic meshing force of gear considering eccentricity(Before optimization)

图13 考虑偏心的齿轮动态啮合力(优化后)Fig.13 Dynamic meshing force of gear considering eccentricity(After optimization)

5 结 论

(1)利用有限元法建立了大型矿用齿轮传动系统参数化动力学模型,通过Newmark时域积分法求解动力学方程得到数值解集,以此反映设计参数与布局参数和动力学响应之间的映射,在此基础上建立同时考虑设计参数与布局参数的优化模型。

(2)通过优化后模型与原始模型求解的动态数值计算结果对比说明,NSGA-Ⅱ算法对大型矿用齿轮传动系统的动态性能优化设计十分有效,多目标优化后两级齿轮动态啮合力分别降低7.6%与15.7%,体积降低27.0%。

(3)对于大型矿用齿轮传动系统,由于齿轮箱体积与结构对大型矿用齿轮箱与性能具有显著影响,因此对于矿用传动系统的设计,多目标优化的结果更合适。