不同风场中特高压换流站阀厅屋盖风压特性试验研究

汪之松, 王宇杰, 余 波, 徐 晴, 何 勇, 李正良

(1. 重庆大学 土木工程学院,重庆 400045; 2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045; 3. 中国电力工程顾问集团西南电力设计院有限公司,成都 610021)

阀厅是换流站的核心建筑,其主体一般采用单层单跨的钢结构,屋面多为坡度较小的直立锁边金属板屋面。在风荷载作用下,阀厅屋面板的风揭事故多发,从而造成阀厅关键设备损坏,严重影响电力系统的正常运转。作为重要的围护结构,阀厅金属屋面的设计风压通常采用规范规定的良态风下的极值风压,且一般只考虑结构主轴方向的风荷载[1]。然而,由于实际气候复杂多变,在对围护结构设计风荷载取值时,不仅要考虑大气边界层风场的影响,也不能忽视雷暴风等极端风场的作用,因此,进行不同风场作用下全风向角工况的阀厅屋面风压分布特性研究十分必要。

对低矮建筑的屋面极值风压分布规律的研究已经被广泛开展。Tieleman等[2-3]在风洞中研究了来流中湍流强度的不同对低矮建筑物表面风压的影响,发现当湍流积分尺度在某些范围之内时,屋面角部区域测点的峰值风压系数和脉动风压系数受到较大的影响。Hoxey等[4-5]基于风洞试验对不同雷诺数下双坡屋面旋涡再附处测点的风压特征进行了分析,发现在迎风前缘处和屋脊分离区测点的风压雷诺数效应明显。傅继阳等[6]在风洞试验中对某大跨悬挑平屋盖结构进行了研究,讨论了均匀流和大气边界层B类风场下该结构的局部体形系数和极值分布规律,发现在两种风场的平均与脉动风压上都具有显著差别。董欣等[7]基于平屋盖风洞刚性模型测压试验结果,分析了均匀流场与湍流流场作用下锥形涡的作用特点。秦乐等[8]分析了风向角、风速、屋盖厚度和场地环境等参数对大跨屋盖的风压分布特性的影响,重点讨论了锥形涡对屋面风压的影响,引入斜度与峰态值来区分屋面风压的高斯与非高斯区域。

在下击暴流风场模拟方面,壁面射流能够较好模拟下击暴流的出流段,并且因模型比例尺不受限制而得到广泛应用。Letchford等[9-10]采用倒立的射流装置来实现静止和移动下击暴流模拟,并研究了下击暴流作用下立方体块的表面风压分布规律,并与均匀流和边界层风结果相比较。王超等[11]分别采用冲击射流和壁面射流两种模型进行数值模拟,表明二者风速水平分量在径向各位置均吻合良好,这为采用壁面射流在大气边界层风洞中实现大比例尺的下击暴流出流段的模拟提供了参考。段旻等[12]在常规大气边界层风洞中得到了平均风速剖面与经验模型相吻合的下击暴流风场,并对圆柱形大跨屋盖的风压特性进行了分析。钟永力等[13]通过在壁面射流中引入协同流的方法来模拟下击暴流的移动增大效应,得到了下击暴流任意水平移动速度下的最大平均风剖面。

在计算屋面极值风压时,峰值因子法通常假设风压时程服从高斯分布,并基于零值穿越理论给出峰值因子,将其乘以时程的标准差来考虑风压的脉动成分。Gioffre等[14]通过与高斯模型比较发现,非高斯风压导致的结构破坏程度比高斯风压的大15%～30%,所以需要重视屋面风压的非高斯特性。庄翔等[15]根据风洞试验的测压结果,用三阶、四阶矩来进行高层建筑表面高斯与非高斯区域的划分,并采用了Hermite级数、全概率迭代和Sadek-Simiu法来计算峰值因子,并对Hermite级数中的各项参数进行了简化,其得到的三参数Heimite矩法与改进的Hermite矩法相比差距较小。叶继红等[16]采用三阶、四阶统计量及柯尔莫哥洛夫检验法研究了五种模型屋面风压,发现在迎风前缘区域及尾流区域非高斯特性较强。

本文研究对象为典型特高压换流站阀厅,其几何尺寸为77.8 m×32.6 m×32.0 m(长×宽×高),双坡屋面坡度为5°,是一个外形规则的单层钢结构建筑。虽然现有文献对低矮坡屋面处于边界层风中的风压特征研究已相当丰富,但建筑高度多小于24.0 m,对达到32.0 m高度的阀厅屋面鲜有研究。且使用壁面射流装置对于下击暴流风场中屋面极值风压的研究更为少见。鉴于特高压换流站阀厅屋面的抗风揭工程需求,本文通过刚性模型的测压风洞试验,探讨边界层风场、壁面射流风场和均匀湍流风场中建筑屋面风压的分布规律,为该类屋面的抗风揭设计取值提供参考。

1 风洞试验概况

1.1 试验装置

测压试验在重庆大学复合直流风洞中进行,试验段尺寸为18.0 m×2.4 m×1.8 m(长×宽×高),具备壁面射流的模拟功能[17]。壁面射流喷口位于试验段起始处,高度为60 mm,宽度与边界层风洞一致,最大射流风速可达到45 m/s。壁面射流装置如图1(a)所示,风洞内壁面射流入口如图1(b)所示。采用壁面射流模拟下击暴流风场的原理示意图如图1(c)所示,其中:Uc为主风洞风机均匀流风速;Uj为壁面射流风速,由壁面射流装置产生;得到的混合风场剖面最大风速为Um,最大风速高度为ym。大气边界层风场和均匀湍流风场分别采用尖劈、粗糙元和格栅在主风洞中实现。模型在壁面射流、边界层和均匀湍流风场中的试验照片分别如图1(b)、图2(a)和图2(b)所示。

图1 壁面射流装置、壁面射流试验与风场原理Fig.1 Wall-jet device, wall-jet test and wind field principle

图2 大气边界层风与均匀湍流风洞试验Fig.2 Wind tunnel test of ABL wind and homogeneous turbulence flow

1.2 试验模型及工况

测压试验模型缩尺比为1∶100。阀厅屋面为双轴对称,测点布置分为A,B,C,D,E,F6个区;测点在屋面边缘位置加密,总计共378个测点。试验风向角为0°～90°,每15°一个工况,共7个风向角。测点布置分区、编号规则与风向角示意如图3所示。

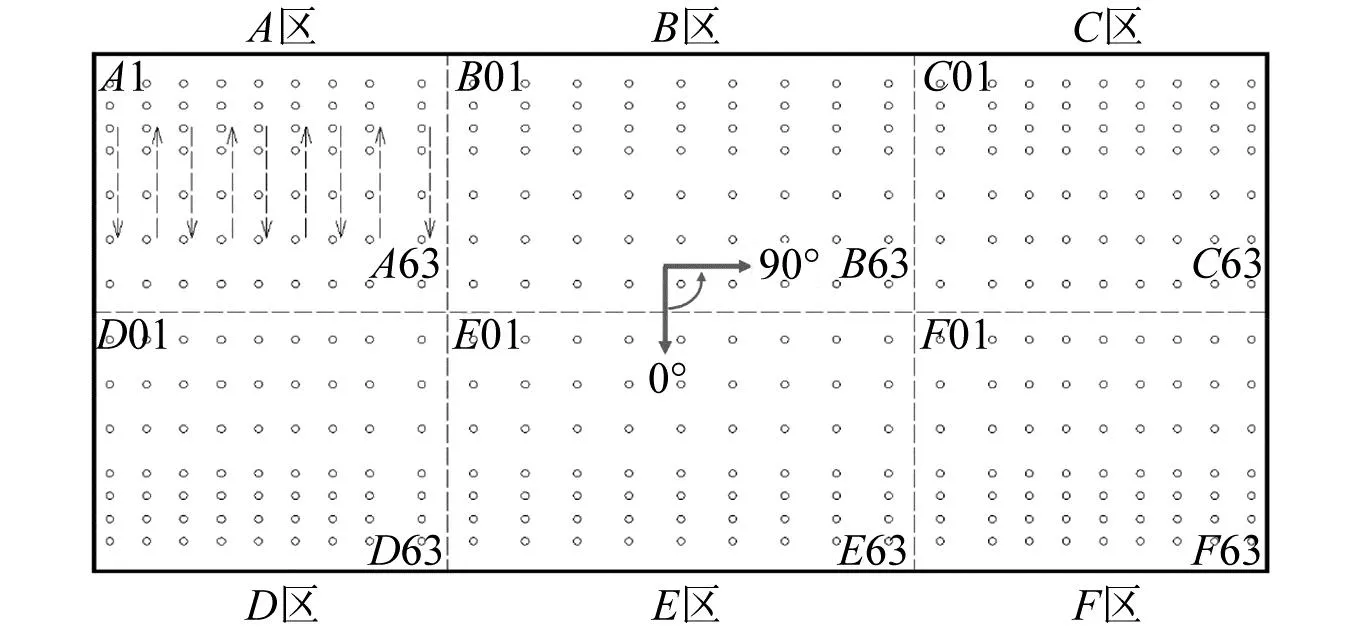
图3 阀厅屋盖测点布置与风向角示意图Fig.3 The pressure measuring points on valve hall roof and wind direction in the tests

本次试验考虑B类大气边界层风场,均匀湍流分别考虑三种风速和三种湍流度,以及壁面射流模拟的下击暴流风场。总体试验工况如表1所示,其中UH为参考点高度处风速,本文试验参考点高度取为建筑顶面高度0.32 m。

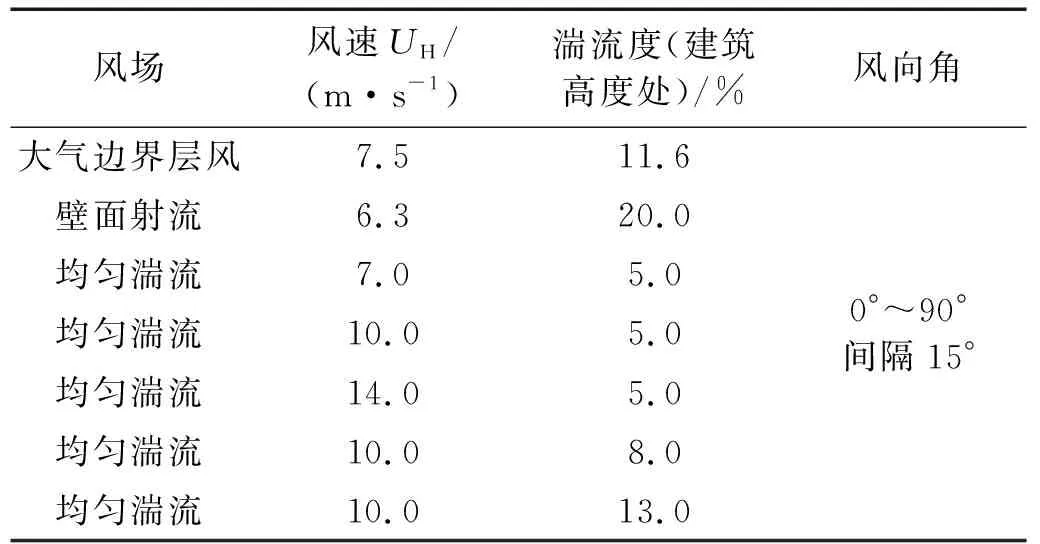
表1 风洞试验工况设置Tab.1 Wind tunnel test conditions

1.3 试验与理论、经验模型对比

1.3.1 大气边界层风场

采用Cobra探头获取不同高度的风速,得到该位置处的平均风剖面及湍流度剖面与理论值对比如图4所示。

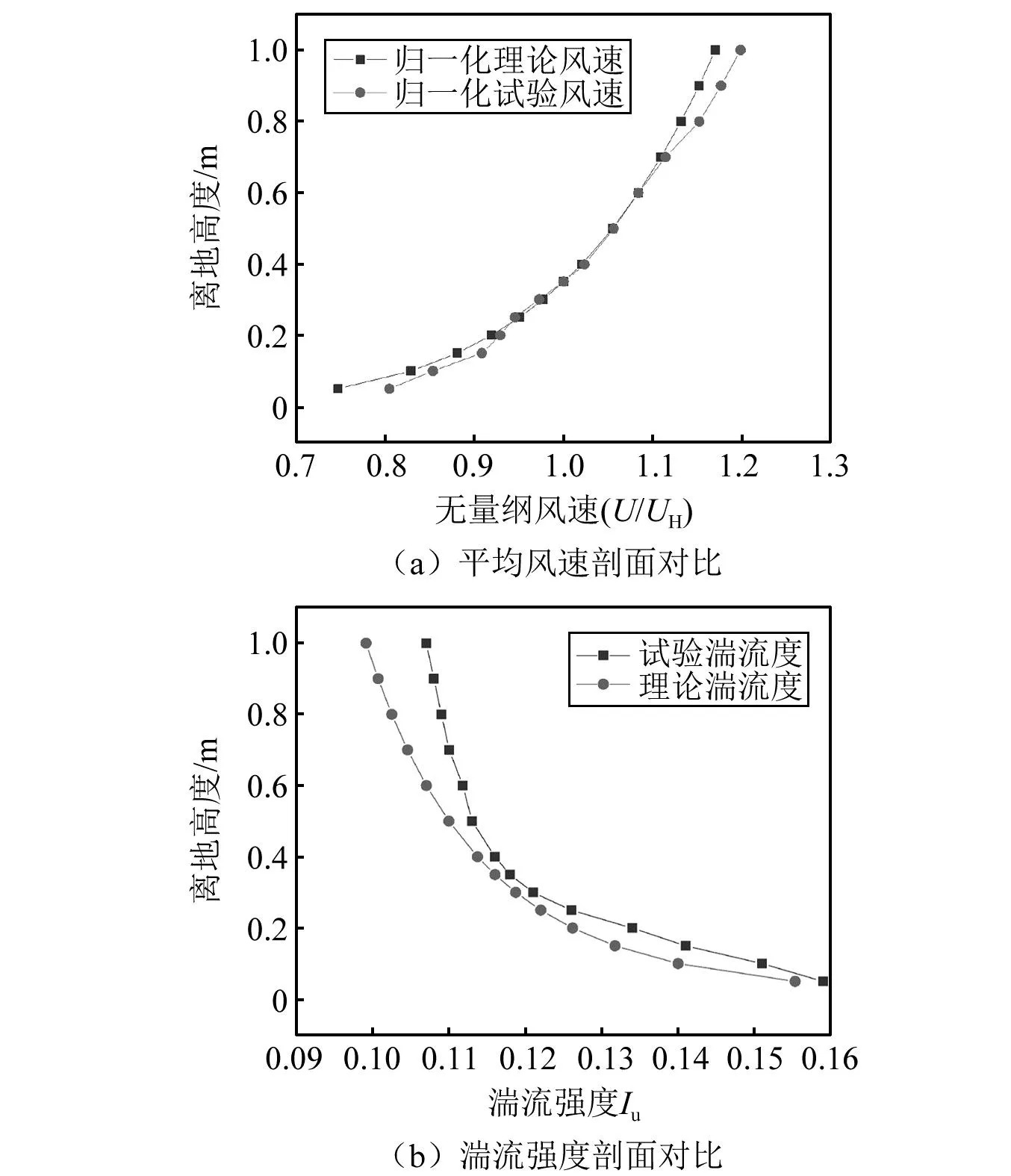
图4 风洞试验与理论剖面对比Fig.4 Comparison of wind profiles of test and theoretical model

在建筑模型高度范围内,试验风场基本吻合理论值。图5为来流参考高度处无量纲化的风速谱,横坐标为折减频率,即fH/UH,为了方便对比,图中还给出了Kamial谱和我国规范建议的Davenport谱。

图5 顺风向脉动风速功率谱Fig.5 The power spectrums of windward wind speed

1.3.2 壁面射流风场

图6为试验和各模型水平速度的无量纲化风剖面,横坐标以最大水平风速Um进行无量纲化,纵坐标以Um相对应的zm进行无量纲化。

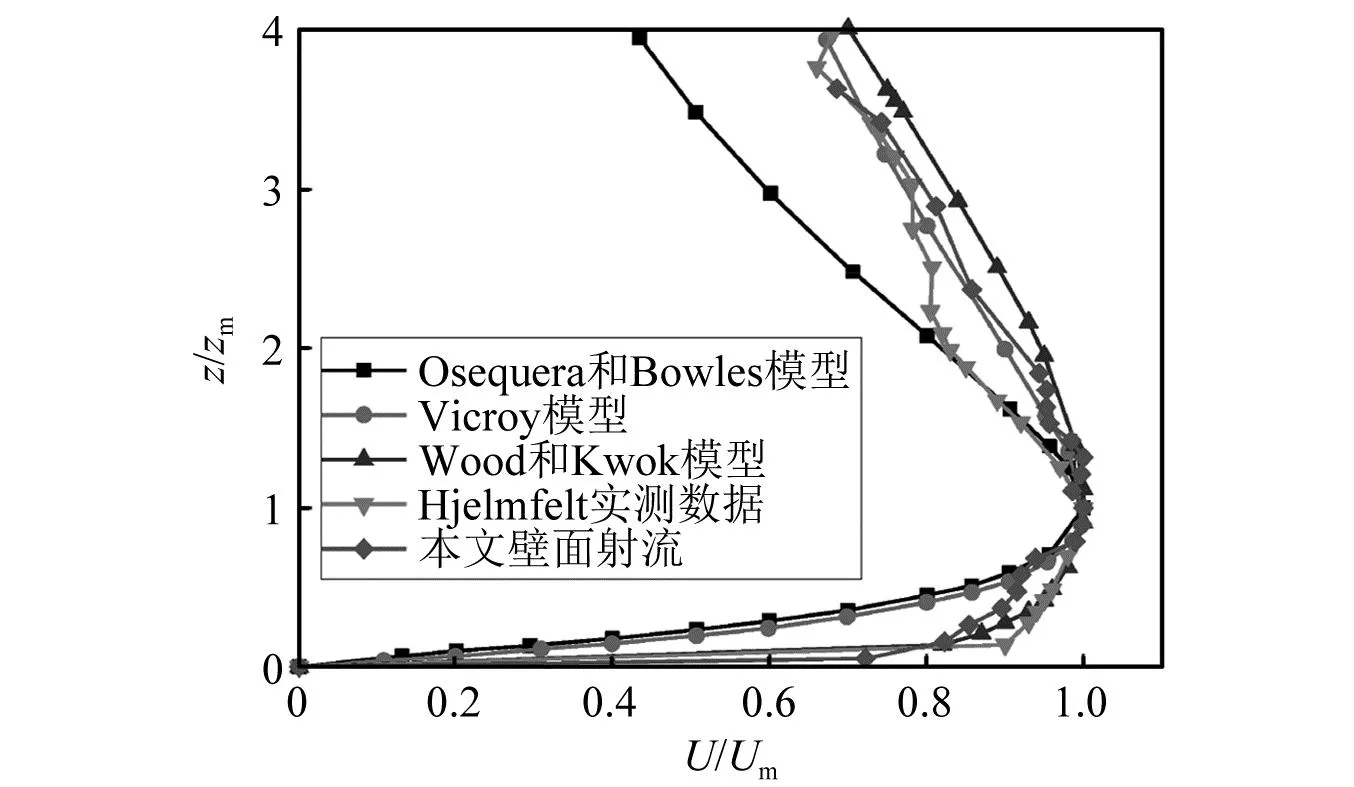
图6 水平速度的无量纲竖向风剖面对比Fig.6 Comparison of non-dimensional vertical wind speed profiles by different models

所有的经验模型在zm高度以下的水平风速都比实测的结果小,OB模型[18]无论是内层还是外层与实测结果都相差较大,Vicroy模型[19]、Wood模型[20]在外层与实测结果符合的较好,壁面射流得到的数据相较于其他模型与实测吻合的程度较高,此次试验的水平风速竖向风剖面与Wood模型吻合较好。壁面射流的极值风速出现在200～300 mm的高度范围内,与阀厅建筑模型高度相近。

1.3.3 均匀湍流风场

图7为均匀湍流风场试验的平均风剖面和湍流强度剖面。试验风速分三档:Ua=5 m/s,Ub=10 m/s,Uc=14 m/s;湍流强度也分为三档:Ia=5%,Ib=8%,Ic=13%。对于试验的平均风速,当风速较低时平均风剖面基本保持竖直;随着试验风速的增大,风洞壁面效应对近地面风速影响增大,但与设计风速相差不超过1 m/s,基本可以认为是均匀湍流场。

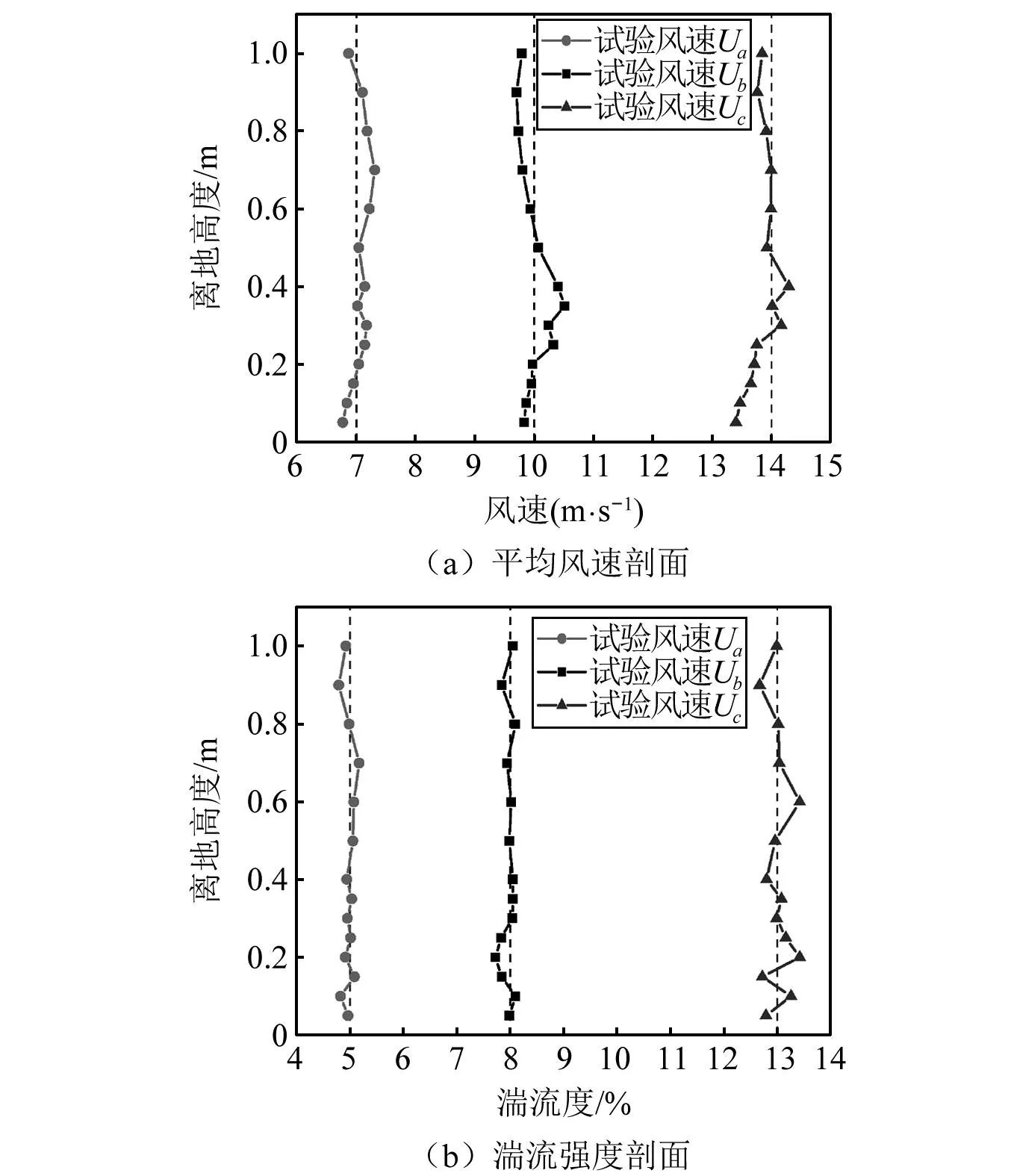
图7 均匀湍流试验风场Fig.7 The profiles of mean wind speed and turbulence intensity of the homogeneous turbulence test wind field

湍流强度较低时,湍流度沿高度分布基本稳定;湍流强度达到13%时,其沿高度分布出现明显波动,本文主要关注屋盖附近流场,故取建筑物顶面高度处的湍流强度作为该工况下的湍流度。

2 屋面测点风压统计特征

2.1 平均风压系数

风洞试验测压系统采用PSI电子压力扫描阀,采样频率约为333 Hz,屋面无量纲风压系数时程计算公式为

(1)

式中:Cpi(tn)为测点i处tn时刻的压力系数;Pi为测点i处测得的压力,Pa;P0和P∞分别为试验时参考高度处的总压和静压,Pa;ρ为空气密度,kg/m3;UH为参考高度风速,m/s。

平均风压系数Cpi,mean的计算式

(2)

式中,N为采样数。

由试验得到大气边界层风场、壁面射流风场和均匀湍流风场下的阀厅屋面平均风压系数分布规律基本类似,只是局部区域系数大小有区别,限于篇幅,此处仅给出大气边界层与壁面射流的屋盖平均风压系数云图,如图8和图9所示(风向角与测点布置见图3)。

图8 大气边界层风阀厅屋盖平均风压系数Fig.8 The mead wind pressure coefficient of valve roof in the ABL flow

图9 壁面射流风场阀厅屋盖平均风压系数Fig.9 The mead wind pressure coefficient of valve roof in wall-jet flow

由图8可知,大气边界层风场作用下,平均分压系数均为负值,且在迎风前缘的平均风压系数绝对值较大,在经过一定范围后,平均风压系数的值趋于平缓。在0°和90°风向角下,风压分布沿流动方向存在明显从大到小的分层梯度变化;45°风向角时,受到角部锥形涡影响,风压在迎风屋面角部沿45°斜向呈对称分布,两侧角部出现最不利平均风压系数为-1.51。

对比图8和图9可发现,两种风场下风压梯度变化趋势基本一致,但风压大小存在差异。特别是45°风向时,壁面射流下在迎风前缘位置的最不利平均风压系可达-2.30左右。由此可见屋面风压分布可能随风剖面改变而改变。

为了单独考虑风速、湍流度对屋面风压分布的影响,如图10和图11所示,给出了均匀湍流工况下的风压统计结果,可以发现均匀湍流风场中屋面平均风压系数也基本为负值。在图10中给出了湍流度为5%时三种不同风速的平均风压系数分布情况,图中横坐标为风速7 m/s时的平均风压系数,将其作为基准比较不同风速对屋盖平均风压系数的影响。在0°风向角,不同风速下,屋盖的平均风压系数几乎都处于基准工况10%误差线内,个别点超出了20%误差线。且都表现出平均风压系数分布从-0.30～-0.55较为均匀的特征。在45°风向角下,除了平均风压位于-0.50附近,其余也几乎都处于20%误差线内部。不同于0°的平均风压系数的均匀分布,此时多数点聚集于横坐标-0.10～-0.50,小于-1.0的平均风压系数较少,这是由于极小值仅出现在屋盖的角涡区,所以数量有限。在90°风向角下,屋盖的平均风压系数在0和-0.35附近出现了两个聚集区,当横坐标大于-0.20时,由于基准平均风压系数值较小,所以众多点都超出了20%误差线的范围,而当横坐标小于-0.20时,误差值就处于20%误差线内部。综合来看,当湍流度相同均为5%时,不同风速下,屋盖的平均风压系数除个别测点以外,各风向角下屋面的平均风压系数相差均位于20%误差内,表面风压分布形式基本一致,这说明在本次试验的雷诺数范围(Re≈1.6×106～3.2×106)内风速对于屋面风压分布影响较小。

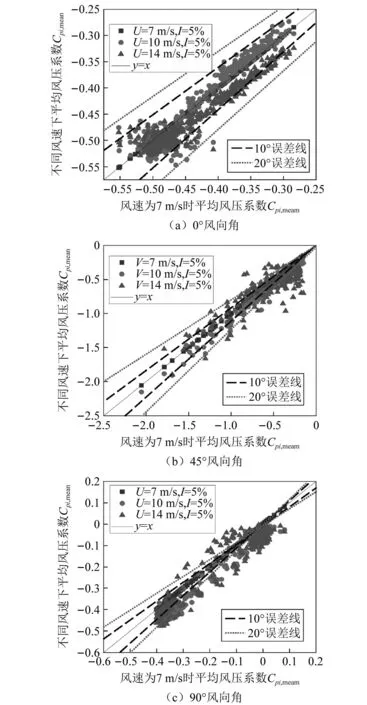
图10 湍流度5%时不同风速下屋面平均风压系数对比Fig.10 Comparison of mean wind pressure coefficients on the roof at different wind speeds while the turbulence intensity is 5%

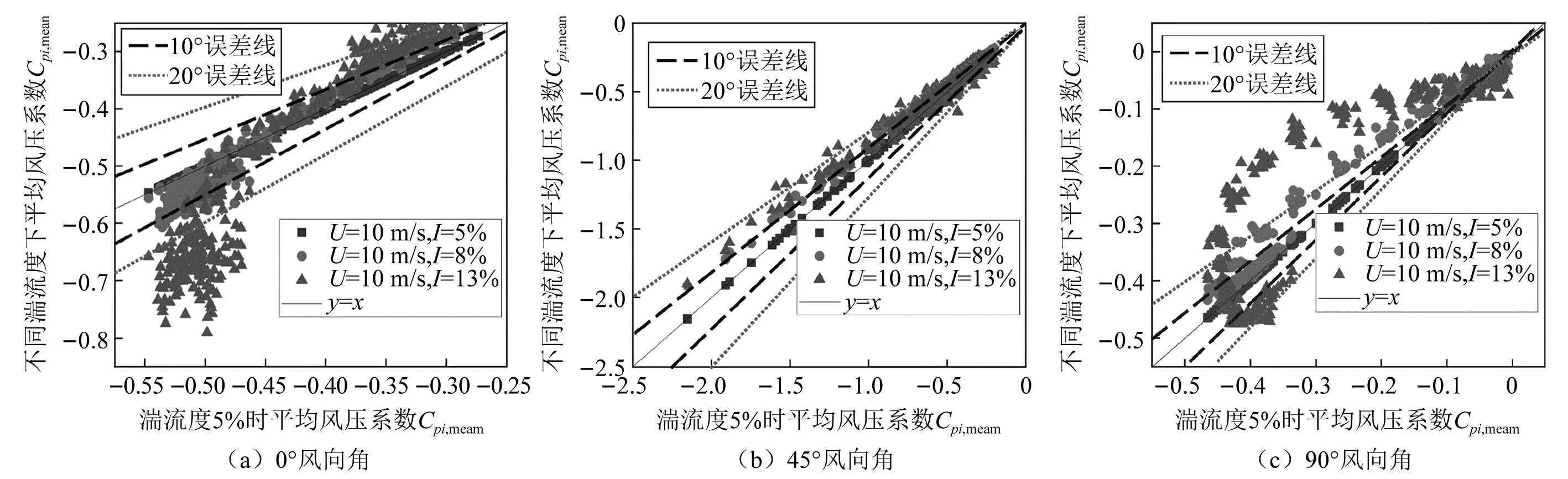
图11 风速10 m/s时不同湍流度屋面平均风压系数对比Fig.11 Comparison of mean wind pressure coefficients of valve roof under different turbulence intensity while the wind speed is 10 m/s

图11给出了同为10 m/s风速时三种湍流度的平均风压系数分布情况。由图11可知,相同风速不同湍流度时,0°和90°风向工况下屋面风压分布差别显著,且湍流度越高,其平均风压系数偏离基准工况越多;在0°风向时,湍流度为8%时,其平均风压系数偏离基准值多位于20%误差线附近;湍流度13%时,平均风压系数已经远超过基准工况的20%误差线。并且较大的湍流度造成极小值风压系数偏离最为严重,这可能与迎风前缘柱涡随湍流度的增大而加强有关。在90°风向时,湍流度为8%,平均风压系数部分超出20%误差线,而13%的湍流度使得平均风压系数大部分都在20%误差线外。而45°风向时屋面风压分布随湍流度变化反而不太明显,基本上都处于10%～20%误差线之间,这表明湍流度对于角涡的生成影响不大。

2.2 脉动风压系数与极小值风压系数

为了研究特征湍流对屋面脉动风压系数与极小值风压系数的影响,给出了阀厅屋面在大气边界层风与壁面射流两种工况下的风压统计量。其中脉动风压系数Cpi,rms

(3)

按我国GB 50009—2012《建筑结构荷载规范》的方法计算屋面负压系数极值

Cpi,min=Cpi,mean-kCpi,rms

(4)

式中:Cpi,mean为平均风压系数;Cpi,rms为脉动风压系数,k=3.5。

图12和图13分别给出了0°与45°工况时大气边界层风场和壁面射流下的屋面脉动风压系数与极小值风压系数。可以看出: 在两类风场下,0°工况时脉动风压系数与极小值风压系数基本呈对称分布,沿屋面分布规律与平均风压系数相似,迎风边角部区域值最为不利;45°风向时,在迎风的两个屋面边缘靠近迎风角附近最为不利,该区域也是锥形涡影响区域,说明锥形涡控制区域内脉动风压系数、极小值风压系数普遍较大。

图12 大气边界层风阀厅屋面风压系数统计量Fig.12 Statistics of wind pressure coefficient on the roof in the ABL wind

图13 壁面射流风场阀厅屋面风压系数统计量Fig.13 Statistics of wind pressure coefficient on the roof in wall-jet flow

对比图12和图13可得,壁面射流下迎风屋面角部区域脉动风压系数和极小值风压系数更大,0°时脉动风压系数和极小值风压系数分别达到了0.39和-2.10,而45°时锥形涡区域脉动风压系数和极小值风压系数分别达到0.95和-5.40。

同样给出均匀湍流的0°和45°工况,来考察湍流度、风速对屋面脉动风压系数的影响。由图14和图15可知,均匀湍流风场下,相同湍流度不同风速时,屋面在各个角度下的脉动风压系数并无较大区别,其差值在0.04范围以内,说明风速的大小对风压系数的影响较小;而相同风速不同湍流度时,脉动风压系数有显著差别,说明湍流度对风压系数影响显著。

图14 湍流度5%时不同风速下阀厅屋面测点脉动风压系数对比Fig.14 Comparison of fluctuating wind pressure coefficients of valve roof at different wind speeds while turbulence intensity is 5%

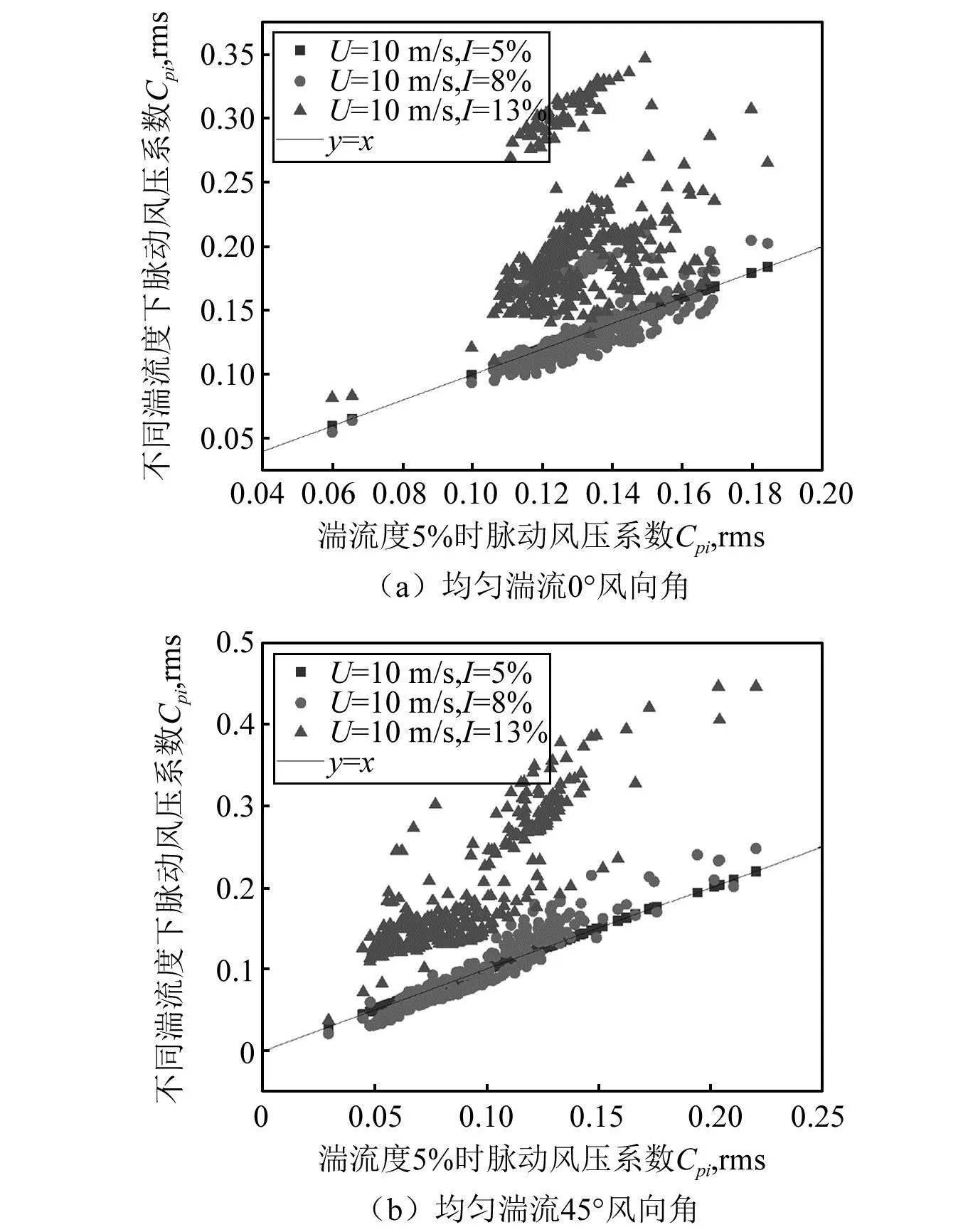
图15 风速为10 m/s时不同湍流度下阀厅屋面测点脉动风压系数对比Fig.15 Comparison of fluctuating wind pressure coefficients of valve roof at different turbulence intensity while wind speed is 10 m/s

屋面风压统计量可以反映绕流场中涡的相关信息,即平均风压系数最小位置的连线可视为涡的中心线,称为涡迹线,脉动风压系数最大的位置可视为涡的再附点[21]。45°工况下的大气边界层风与壁面射流风场的涡迹线与屋面边缘形成的夹角α分别为13.5°和9.72°,这说明在壁面射流风场下,锥形涡的尺度相比于大气边界层有所减小。从图16给出的在不同湍流度下的锥形涡迹线与迎风前缘夹角来看,α随着湍流度增加而呈线性减小,相对应的涡旋尺度降低。

图16 均匀湍流涡迹线与屋缘夹角变化Fig.16 The angle of the vortex trace and the roof edge in the homogeneous turbulent flow

3 屋面风压极值估算

3.1 峰值因子

屋面的破坏往往是湍流引起的风压波动在某一时刻超过设计值而导致的。在风压是平稳随机过程的假定成立的情况下,张相庭[22]认为屋面风压时程围绕均值上下均匀波动,其假定风压的分布为高斯分布,此时风压极值可表示为

Cpi,min=Cpi,mean-gCpi,rms

(5)

式中,g为Davenport峰值因子,计算式为

(6)

式中:T为风压时程的时长;γ为欧拉常数,取为0.577 2;v为零穿越率,计算式为

(7)

式中:S(n)为风压时程功率谱密度;n为频率。

然而来流在经过建筑物时会经历分离、再附着,此时伴随着漩涡的生成与脱落,流场变化剧烈,拟定常假设不再适用。在高湍流风场中,风压具有明显的非高斯特性。采用非高斯峰值因子法计算极值风压系数,其负压极值计算式如下

Cpi,min=Cpi,mean-gnCpi,rms

(8)

式中:Cpi,rms为脉动均方根风压系数;gn为非高斯峰值因子,gn的取值采用基于统计矩的Hermite模型求得。其基本思路为:每一个非高斯过程时程点与高斯过程时程点唯一对应,构造单调函数再进行非线性变换可以将一个非高斯过程用高斯平稳随机过程表达,假设时段T内极值符合Poisson分布,可得到非高斯峰值因子的表达式[23],如下所示

(9)

(10)

(11)

(12)

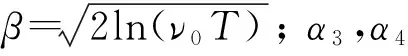
图17 大气边界层风场下屋面测点峰值因子Fig.17 Peak factor of the measuring points on the roof in ABL wind

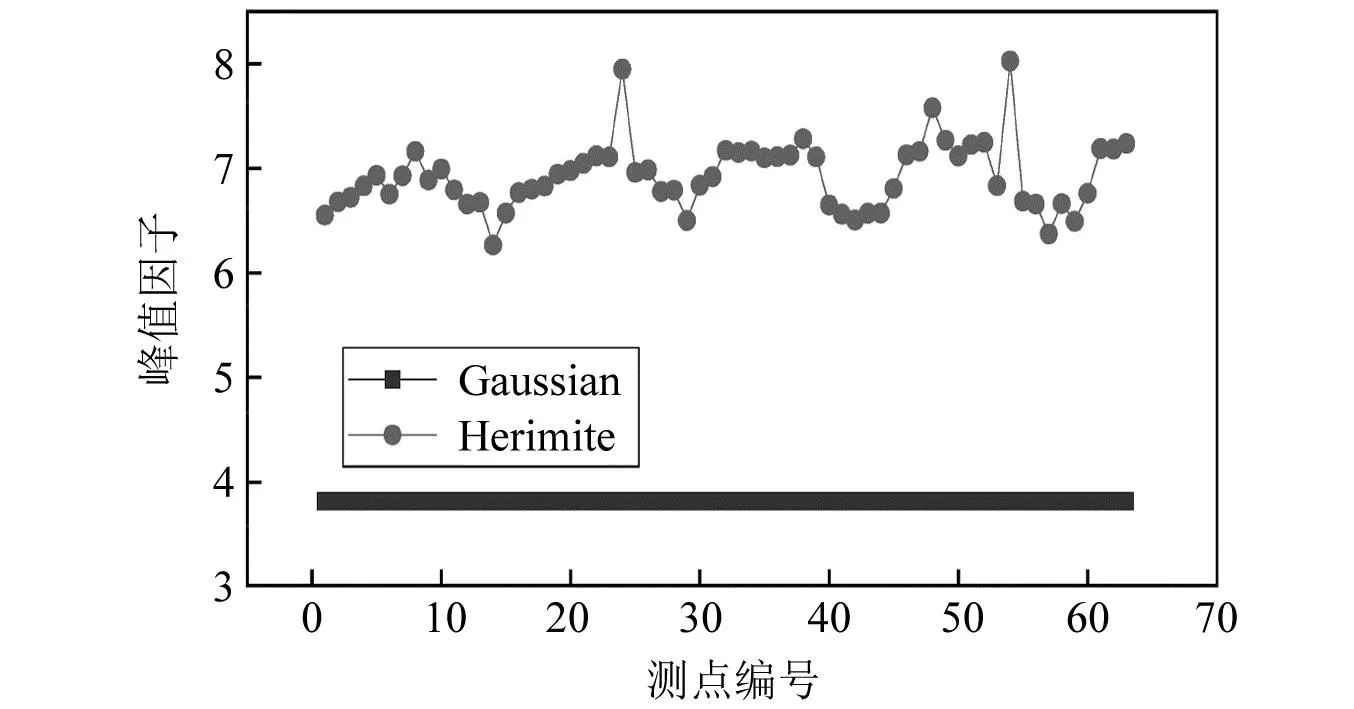
图18 壁面射流风场下屋面测点峰值因子Fig.18 Peak factor of the measuring points on the roof in wall-jet flow

计算结果表明,无论是Davenport基于高斯过程求出极值分布还是Hermite矩法求解峰值因子,都会涉及到零超越率v及时间段T,规定一定时间段内的时程以正斜率超越零界限的次数vT来表征,其取值一般都在100以上,得到的峰值因子常大于3。将Davenport法与Hermite矩法得到峰值因子相比较,前者为一定值,而后者在两种风场作用下都要大于前者,而且后者在壁面射流风场下的取值要大于大气边界层风。相较之下,Hermite矩法求解的峰值因子保证率更高。

3.2 全风向最不利极值风压

在设计中如果按照风压测点的极值来进行围护结构的抗风设计不但会造成设计效率低下,而且由于测点在空间上具有相关性,不一定会在同时刻和同风向达到最不利情况,因此通常取局部面风压系数极值进行设计。

在JGJ/T 481—2019《屋盖结构风荷载标准》[24](下文简称“屋盖标准”)中规定,对于中高层建筑,当屋面坡度在0°<θ≤10°、屋盖平均高度H>20 m或者H/B≥1,H/D≥1时(H,B,D分别为建筑高、长、宽),屋盖围护结构的风荷载分区应按风荷载分区图(如图19所示)确定,其中a取0.1B,0.1D和0.4H中的最小值,且不应小于0.04B和0.04D中较小值,本文a取0.1D。全风向风压系数极值Cpe按表2确定。

表2 中高层建筑屋盖围护结构全风向风压系数最值Tab.2 The maximum wind pressure coefficient in the whole wind direction of the roof of medium and high-rise buildings

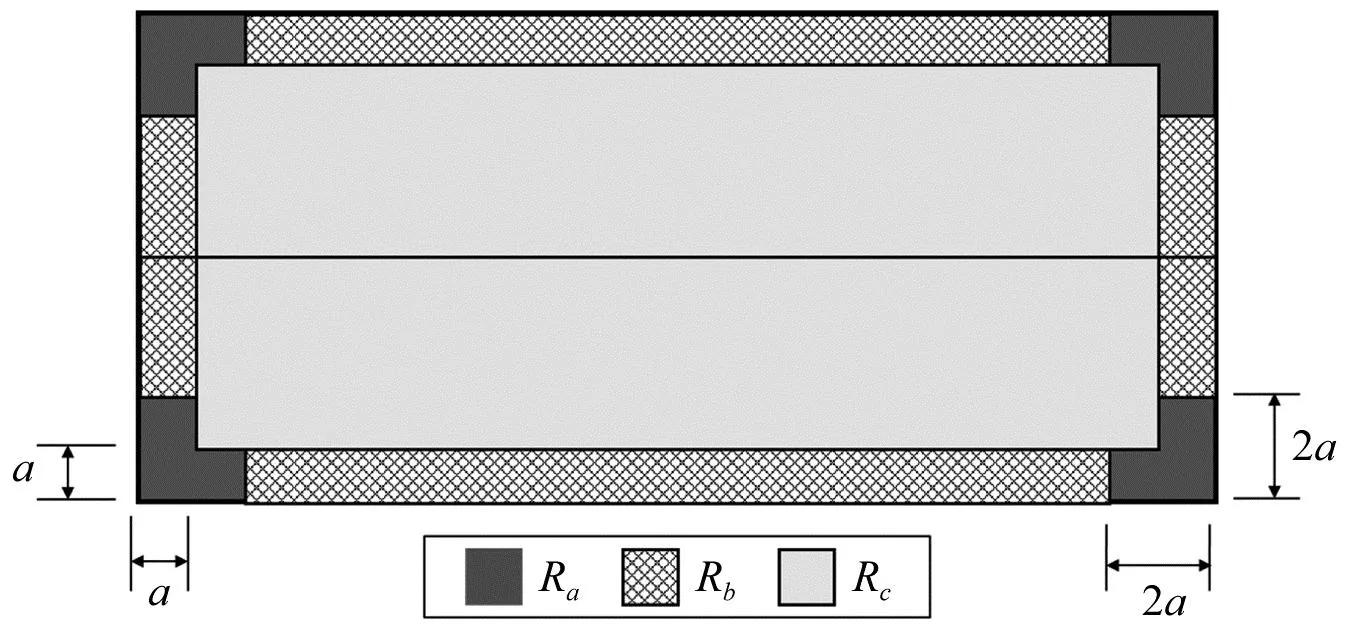
图19 JGJ/T 481—2019《屋盖结构风荷载标准》分区示意图Fig.19 Wind load zoning of the roof that suggested by JGJ/T 481—2019

由测压试验结果结合非高斯峰值因子取值并按公式(5)计算得到测点风压系数极值,按屋盖标准中的分区方法,在各分区中对测点风压系数进行加权平均,并进一步得到各分区的面风压系数极值,如图20所示,图中括号中数值为屋盖标准建议取值。从图中可以看出:在大气边界层风场作用下,风洞试验得到的阀厅屋盖全风向风压系数极值与屋盖标准建议值相比,在角部位置略大,在屋面短边Rb区取值较为接近,而在其他区域,屋盖标准建议值较为保守;来流为壁面射流时,阀厅屋盖全风向最不利系数在各个分区都要超出屋盖标准建议值,采用屋盖标准建议取值进行设计可能会导致阀厅屋面围护结构在极端风场下的不安全。

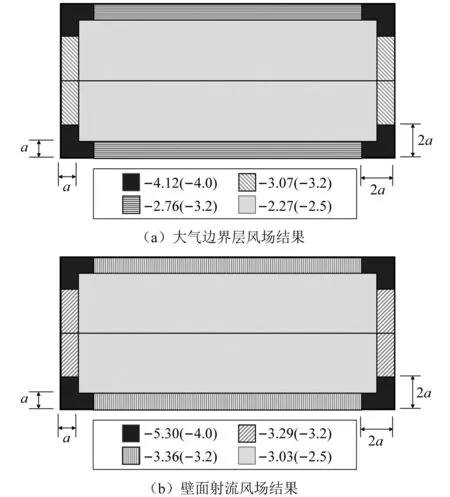
图20 不同风场作用下阀厅屋面全风向风压系数试验极值Fig.20 The maximum value of the wind pressure coefficient in the whole wind direction of the roof in different wind fields by the tests

4 结 论

基于大气边界层、壁面射流和均匀湍流风场下的阀厅模型测压风洞试验,讨论不同风场参数对阀厅屋面风压分布的影响规律,主要结论如下:

(1) 阀厅屋盖迎风前缘负风压最大,沿风向屋面风压梯度变化大。壁面射流风场下平均风压系数与脉动风压系数均超过大气边界层风场下的结果,因此雷暴风等极端气候下的风场是阀厅屋盖围护的最不利风荷载风场,且控制风向角在45°左右。

(2) 均匀湍流风场作用下的结果表明,风速对阀厅屋盖的负风压系数均值和极值影响较小,而湍流度对风压系数的极值影响较大。相同风速不同湍流度工况的结果表明,45°风向角下涡迹线与屋面边缘夹角呈现出随着湍流度的增加而减小的规律。

(3) 阀厅屋盖最不利风压系数的取值方面,在大气边界风场下,除屋面角部区域外,屋盖标准的最不利风压系数建议值偏于保守,按照屋盖荷载标准取值设计是可以保证安全的;但在下击暴流风场下,阀厅屋盖全风向最不利风压系数在所有区域都大于屋盖标准建议值,建议考虑下击暴流极端风环境的屋盖最不利风压系数需要将屋盖荷载规范取值放大1.325倍,并在设计中对屋盖抗风揭加以重视。

由于实际的雷暴风场往往伴随着风暴的移动和风场的非平稳特性,这些因素也会对屋盖的极值风压产生很大影响,可以在以后的研究中进一步深入讨论。