改进Reddy型三阶剪切变形理论下FG-GRC板弯曲和模态分析的无网格法

杨立军, 陈 孔, 陈 卫

(1.湖南文理学院 芙蓉学院,湖南 常德 415000; 2. 中国建筑第八工程局有限公司南方公司,南宁 530004; 3. 南华大学 土木工程学院,湖南 衡阳 421001)

近年来,碳纳米管[1](carbon nanotubes,CNTs)和石墨烯纳米片[2](graphene platelets,GPLs)凭借其优异的电子、光学、热导率和力学性能被广泛应用于聚合物和金属中的增强材料。另外,已经证明在聚合物基体中加入0.1%的GPLS和1%的CNTs,其强度和刚度基本得到了同等改善[3]。GPLs的突出特点有:极高比表面积、高宽径比、高界面黏着性。石墨烯增强复合材料由于其优异的性能,为工程人员在实际工程中开发和设计先进的轻量级结构创造了条件。

功能梯度材料(functionally graded materials, FGM)是一种新型的非均匀复合材料,它是1984年由日本材料学者Koizumi[4]对航天技术中的高落差温度而提出的,其各组分材料可沿一个或多个方向连续梯度变化。2017年,Yang等[5]将FGM的概念引入到石墨烯增强复合材料中,形成了功能梯度石墨烯增强复合材料(functionally graded graphene-reinforced composite,FG-GRC)。嗣后,Feng等[6-7]基于一阶剪切变形理论,采用Ritz法研究了FG-GRC纳米梁的非线性静力弯曲和非线性自由振动行为。Yang等同样基于FSDT理论,采用微分求积法,分析了弹性地基上FG-GRC纳米梁屈曲及后屈曲行为。Song等[8-9]利用基于FSDT的Navier求解技术,对FG-GRC板进行了弯曲、抗压和低速冲击响应分析。Wu等[10-11]基于上述同样的模型给出了FG-GRC板的热屈曲和后屈曲解析解。Reddy等[12]结合FSDT和有限元法,研究了FG-GRC板的自由振动行为。Guo等[13]采用改进的移动最小二乘(improved moving least-square,IMLS)-Ritz法和FSDT相结合,研究了FG-GRC板的自由振动行为。为了保证解的稳定性,在使用FSDT时,还需要在剪切应变能中引入剪修正因子。为了忽略剪切修正因子,需引入了高阶剪切变形理论。Gholami等[14]提出了一种与三阶剪切变形理论(third-order shear deformation theory, TSDT)相结合的变分DQ技术来研究FG GPLRC板的非线性谐激振动行为。庞有卿等[15]采用Navier解答技术给出了新的双曲剪切变形理论(hyperbolic shear deformation theory,HSDT)及TSDT下FG-GRC板自由振动问题的解析解。王壮壮等[16]同样基于Navier解答,对比分析了正弦剪切变形理论(sinusoidal shear deformation theory,SSDT)和TSDT对FG-GRC板的线性弯曲与屈曲的影响。

解析解或半解析法求解的只是少数简单的偏微分方程组,对于工程结构中较为复杂几何模型,边界条件及载荷,很难获得解析解,因而数值类算法显得尤为重要。无网格法作为一种已发展二十年有余的数值算法,在分析板壳问题时虽然相比FEM法具有得天独厚的优势[17],如只需提高形函数的阶次即可完全避免FEM在分析薄板壳问题遇到的剪切锁死现象[18],但因无法准确施加第二类边界条件,大多数文献均是基于FSDT框架下[19-22],结合无网格法,只能处理薄/中厚板问题,限制了无网格法在厚板中的应用。2016年,Selim等[23]假设TSDT位移场中的三阶项为一个独立变量(ψx=φx+∂w0/∂x,ψy=φy+∂w0/∂y),将含5个自由度变量扩展到7个自由度变量,同时避免了第二类边界条件的施加,结合无网格法分析了功能梯度碳纳米管增强复合材料板(functionally graded carbon nanotube-reinforced composite, FG-CNTRC)的自由振动问题。

综上所述,目前对FG-GRC力学性能的研究涌现出不少解析解或基于FSDT理论框架下的数值解,采用基于TSDT的无网格法对FG-GRC板的弯曲及模态研究极为罕见。本文采用稳定移动最小二乘近似(stabilized moving least-square approximation, SMLS)的无网格法,建立分析FG-GRC板线性弯曲与自由振动的无网格模型。其中,为避免无网格法中第二类边界条件的施加困难问题,利用了含7个自由度变量的改进Reddy型TSDT理论框架,该无网格模型不需人工引入剪切修正因子,可分析FG-GRC厚板问题。文中通过算例分析了本文方法的收敛性及有效性,在此基础上进一步数值分析和讨论了GPLs分布模式,质量分数、总层数和边界条件等对FG-GRC板弯曲挠度和自振频率的影响。

1 稳定移动最小二乘近似

设某个域内Ω上的函数u(x)可被函数uh(x)在其子域内Ωx近似[24]

(1)

式中:pi(x)为已知的单项式基函数;m为基函数的个数;bi(x)为待求系数。传统移动最小二乘近似采用pT=[1,x,y,x2,xy,y2]T,但由于传统移动最小二乘近似在节点间距减小时,稳定性削弱,故Li等[25]以相对间距为单项式基函数提出了SMLS

(2)

(3)

式中:w(x-xI)为权函数,在子域Ωx外w(x-xI)=0;N为子域内节点个数;uI为节点参数。令

∂Γ/∂b(x)=0

(4)

则可得

b(x)=B-1(x)A(x)u

(5)

其中,

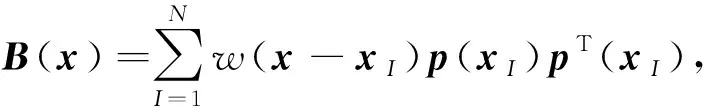
将式(5)代入式(1),则有

(6)

其中,

NI(x)=pT(x)B-1(x)p(xI)w(x-xI)

(7)

2 数学模型

2.1 材料性质

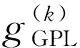
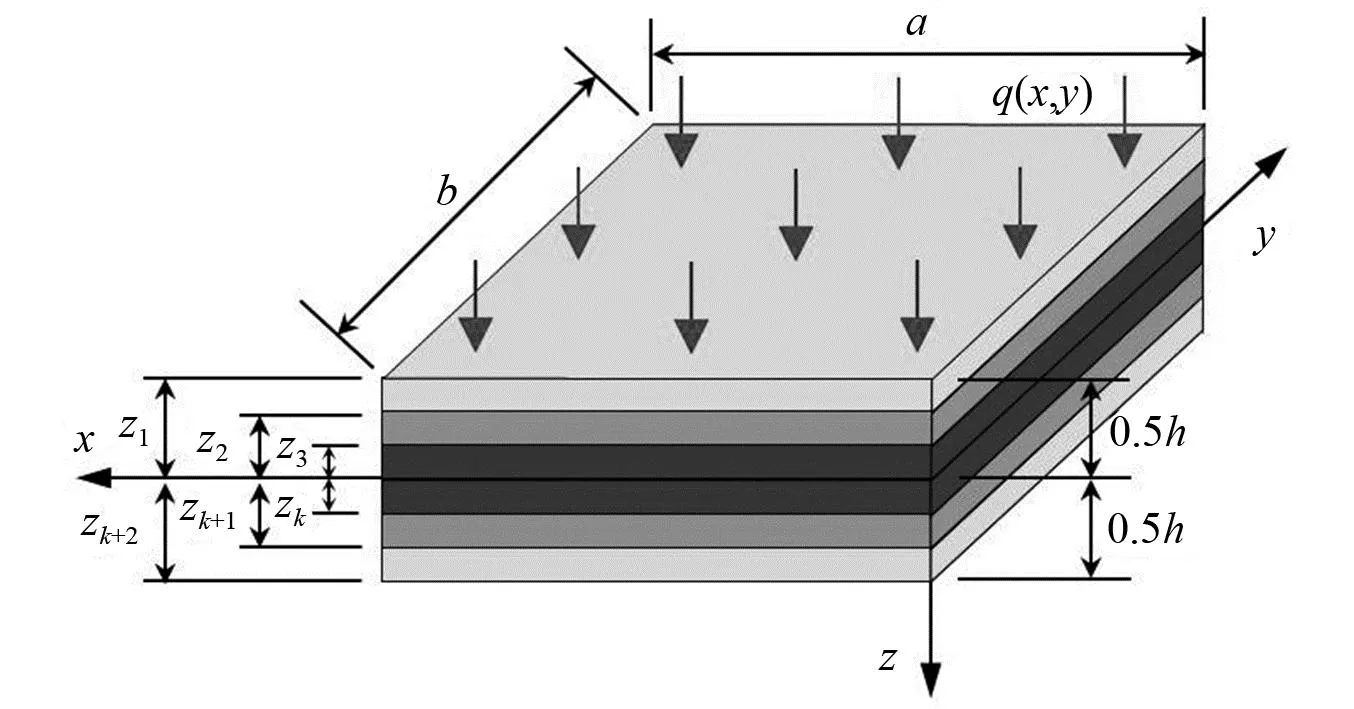
图1 FG-GRC板示意图Fig.1 Schemtaic of functionally graded graphene-reinforced composite plate

图2 GPLs分布模式Fig.2 Graphene nanoplatelets distribution patterns

(8)

式中,gGPL为GPLs的质量分数,k=1,2,3,…,NL。

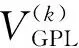
(9)

式中,ρGPL和ρM分别为GPLs和基体的质量密度。

根据修正的Halpin-Tsai模型[26],第k层GRC的有效弹性模量为

(10)

其中,

(11)

式中:EGPL和EM分别为GPLs和基体的弹性模量; 下标GPL,M,C分别为GPLs、基体以及石墨烯增强复合材料;ξl和ξw分别为表征石墨烯纳米材料的几何形状和尺寸的参数,定义如下

(12)

式中,lGPL,wGPL和hGPL为GPLs的长、宽、高。

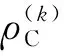
(13)

(14)

2.2 总能量泛函

根据Reddy’s三阶剪切变形理论[27],含5个自由度的广义位移场U=(u,v,w)T可表示为

(15)

式中: (u0,v0,w0)T为板中面任意一点在x,y,z方向的位移;φx,φy分别为绕y轴和x轴的转动;c=-4/3h2。根据文献[28],假设ψx=φx+∂w0/∂x,ψy=φy+∂w0/∂y,式(15)则可改写为含7个自由度变量的广义位移场如下

(16)

根据几何方程,板的面内应变和剪切应变分别为

ε={εxεyγxy}T=ε0+zκ1+z3κ2

(17)

γ={γyzγxz}T=εs+z2κs

(18)

其中,

ε0={u0,xv0,yu0,y+v0,x}T,
κ1={φx,xφy,yφx,y+φy,x}T,
κ2=c{ψx,xψy,yψx,y+ψy,x}T,
εs={φx+w0,xφy+w0,y}T,
κs=3c{ψxψy}T

第k层FG-GRC板的应力-应变关系为

(19)

其中,

(20)

FG-GRC板的内力和应变关系为

(21)

其中,

(Aij,Bij,Dij,Eij,Fij,Hij)=

(22)

(23)

FG-GRC板的应变能为

(24)

FG-GRC板受横向荷载q(x,y)的总势能泛函为

(25)

FG-GRC板的动能为

(26)

将式(24)和式(26)进行叠加,则FG-GRC板自由振动时的总势能泛函为

Πs=Up-T

(27)

2.3 控制方程

对FG-CNTRC板的节点位移及转角进行离散,利用式(6)近似得到

(28)

将式(28)代入式(25),根据最小势能原理,δΠu=0,则FG-GRC板线性弯曲的无网格控制方程为

KU=F

(29)

(30)

其中,

U=[uIvIwIφxIφyIψxIψyI]T,

其中,

3 本质边界条件

由于基于移动最小二乘近似得到的形函数不满足Kronecker条件,各节点未知量是节点参数而非真实位移,本文采用Chen等[29]提出的完全转换法处理本质边界条件。

(31)

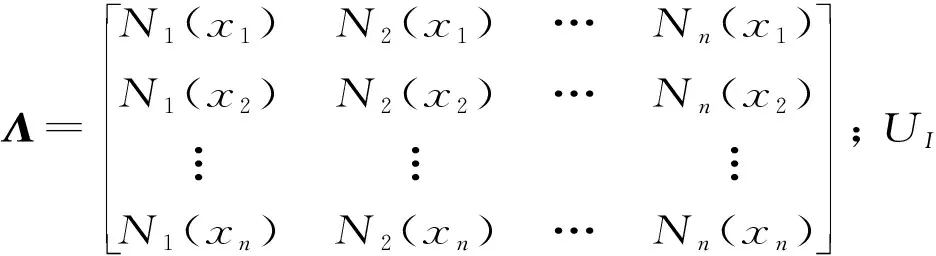
(32)

将式(32)代入式(29)得到

(33)

上式两边同乘TT,则有

(34)

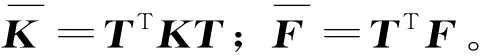
同理,式(30)可修改为

(35)

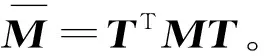
通过解如下方程的特征值问题,可得到FG-GRC板的自振频率。

(36)

4 数值结果与分析

本章首先以四边简支FG-GRC板的弯曲和基频为例,将计算结果与文献中的解析解进行对比,验证本文方法的收敛性及有效性,接着运用本文方法分析GPLs分布模式、质量分数、总层数及边界条件对FG-GRC板的弯曲及自振频率的影响。

数值试验中,FG-GRC板结构考虑如下常见的3种边界条件,以x=0,a边界为例,则有:①固支边界(Clamped, C)u=v=w=φx=φy=ψx=ψy=0;②简支边界(Simply, S)v=w=φy=ψy=0;③自由边界(Free, F)没有限制。

4.1 收敛性分析

为验证本文方法计算FG-GRC板弯曲(均布荷载q0=500 kPa)与自振频率收敛性,取均布无网格节点数5×5,7×7,11×11,15×15对四边简支(SSSS)或四边固支(CCCC)FG-GRC板的无量纲中心挠度及基频进行收敛性分析,计算结果及解析解列于表1和表2。由表1和表2可知,采用本文方法计算FG-GRC板弯曲及自振频率具有较好的收敛性。当节点数为11×11时:①本文方法对四边简支FG-GRC板挠度与基频的计算结果与王壮壮等研究中基于正弦剪切变形理论得到的解析解误差在0.001%以内;②四边固支FG-GRC板基频与文献中基于广义高阶剪切变形理论的等几何分析(isgeometric analysis, IGA)数值结果误差在0.7%以内。由此可认为该离散方案已使得计算结果收敛,后续算例均采用11×11节点离散。

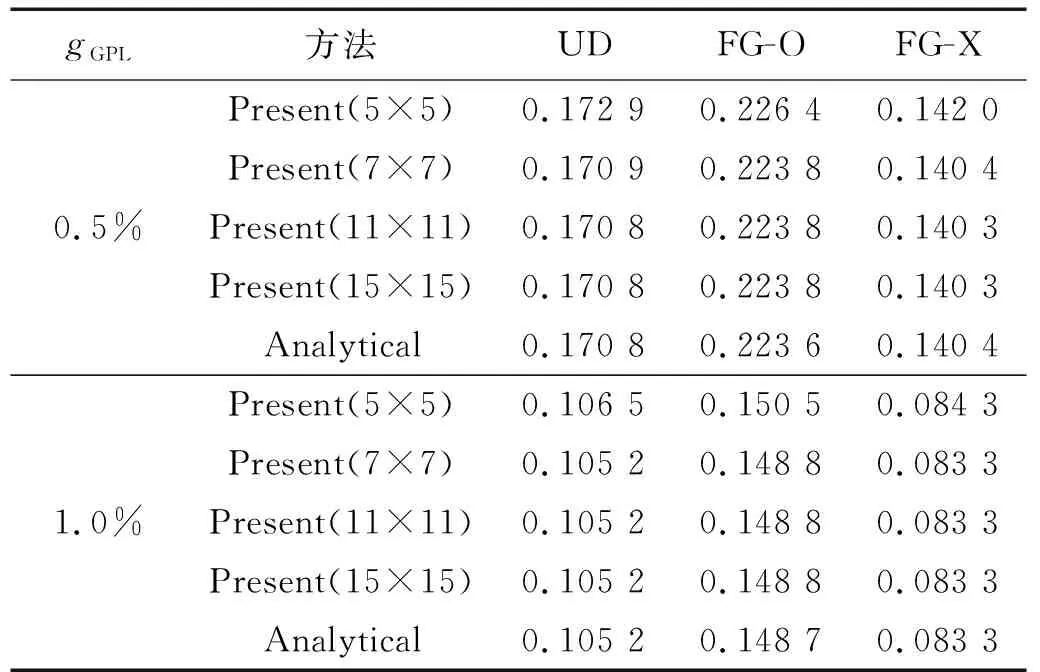
表1 不同GPLs质量分数下四边简支FG-GRC板的无量纲中心挠度收敛性分析Tab.1 Convergence analysis of dimensionless central deflection of simply supported FG-GRC plates under different weight fractions gGPL

表2 四边简支或固支FG-GRC板无量纲基频收敛性分析Tab.2 Convergence analysis of dimensionless fundamental frequency of simply supported or clamped FG-GRC plates

4.2 弯曲分析

表3计算了CCCC、CSCS、CFCF和SSSS 4种边界条件下FG-GRC板的无量纲中心挠度,其中SSSS边界条件下本文的计算结果与基于三阶剪切变形理论的解析解吻合良好,证明了本文方法计算FG-GRC板弯曲的准确性。由表3可知,随着边界约束的增强,FG-GRC板的中心挠度减少;环氧树脂板的中心挠度均大于FG-GRC板,说明GPLs极高的弹性模量可有效增加FG-GRC板的刚度;不同GPLs分布模式下FG-GRC板结构刚度存在较大的差异,按照GPLs分布模式形成的结构刚度大小依次为:FG-X>UD>FG-A>FG-O。

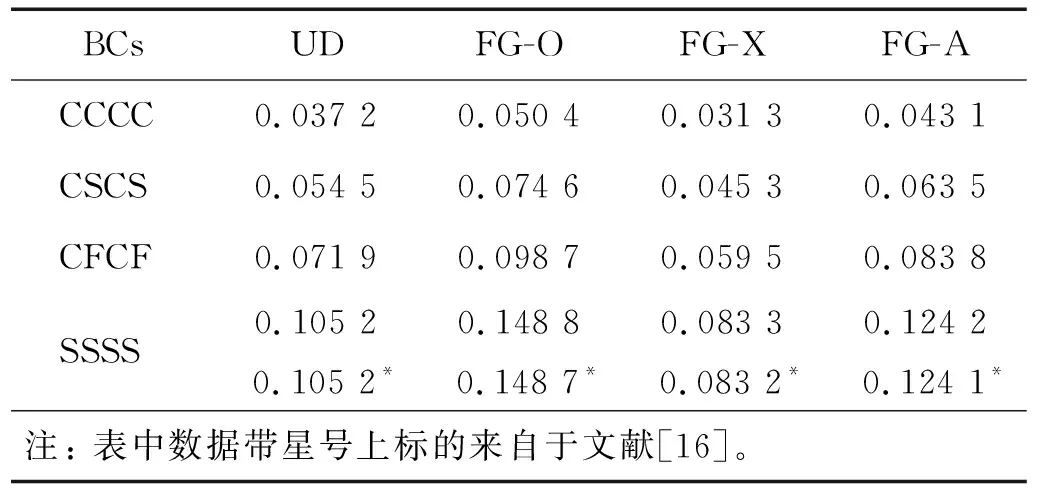
表3 不同边界条件下FG-GRC板的无量纲中心挠度Tab.3 Dimensionless central deflection of FG-GRC plate under different boundary conditions

图3和图4分别展示了GPLs的分布模式、总层数NL和质量分数gGPL对FG-GRC板的无量纲弯曲挠度变化率Dc的影响,其中Dc=wC/wM×100%,wC和wM分别表示FG-GRC板和环氧树脂板的无量纲挠度中心数值。可以看出:4种GPL分布模式的情况下,FG-X的补强效果最好,其次是UD,FG-A和FG-O,GPLs均匀分布模式(uniformly distributed,UD)的板的挠度不受NL的影响;FG-O和FG-A板的挠度随着NL的增加而增加,而FG-X板的挠度随着NL的增加而减小;当FG-GRC板的总层数NL<10～15时,FG-X、FG-A和FG-O分布模式下的板弯曲挠度变化率较为剧烈,说明该阶段相较于环氧树脂板,GPLs增强板的挠度降低(或增加)较快;当FG-GRC板的总层数NL>10～15时,板弯曲挠度变化率较为平缓;随着重量分数gGPL的增加,板的弯曲挠度变化率逐渐减少,由此可以说明,GPLs的含量增加可以显著提高FG-GRC板的刚度。

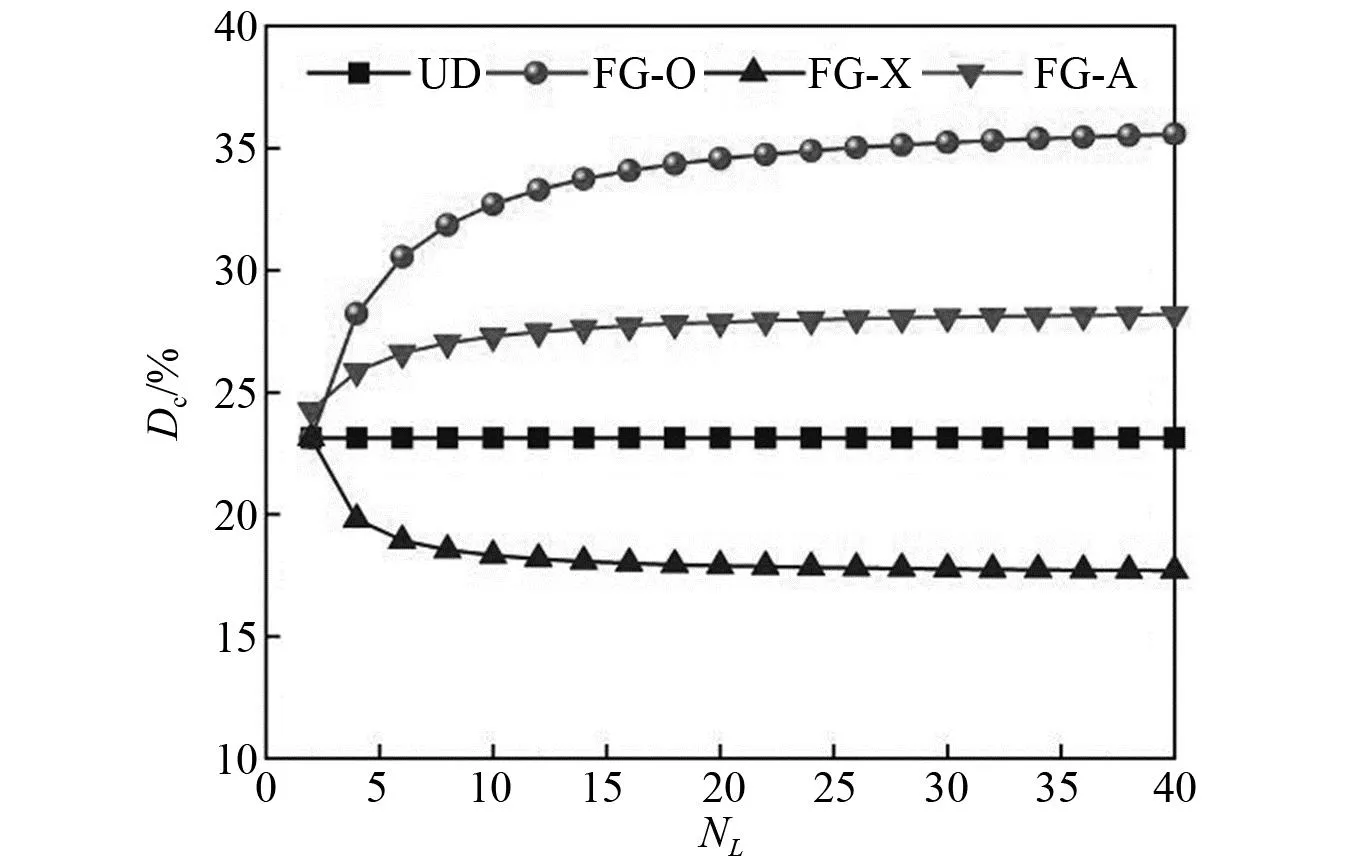
图3 总层数NL对FG-GRC板Dc的影响Fig.3 Effect of total number of layers NL on the percentage defection change Dc of the FG-GRC plates

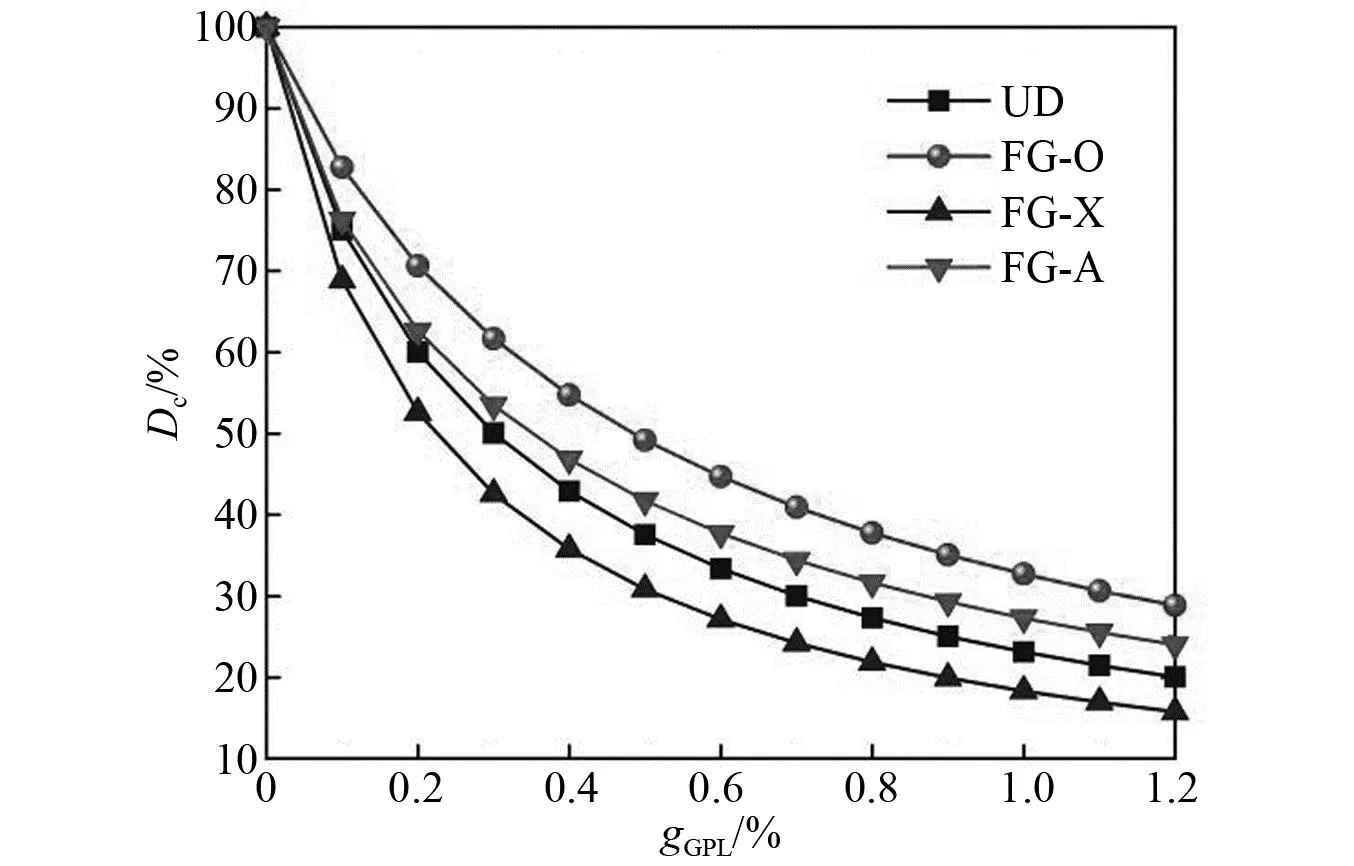
图4 质量分数gGPL对FG-GRC板Dc的影响Fig.4 Effect of weight fraction gGPL on the percentage defection change Dc of the FG-GRC plates

图5讨论了GPLs的分布模式、长宽比lGPL/wGPL和长厚比lGPL/hGPL对FG-GRC板的无量纲弯曲挠度变化率Dc的影响。数值计算时,固定lGPL=2.5 μm不变,变化wGPL和hGPL。研究发明:随着lGPL/hGPL增加到1 000左右,FG-GRC板的无量纲弯曲挠度变化率急剧降低,然后随着lGPL/hGPL的进一步增加而降低非常缓慢;方形GPLs(lGPL/wGPL=1.0)增强FG-GRC板的弯曲挠度比矩形GPLs(lGPL/wGPL=3.0)增强FG-GRC板弯曲挠度小,这是因为方形GPLs(lGPL/wGPL=1.0)增强FG-GRC板具有较高的表面积,GPLs与基体之间较大的接触面积,导致了更高的结构刚度。

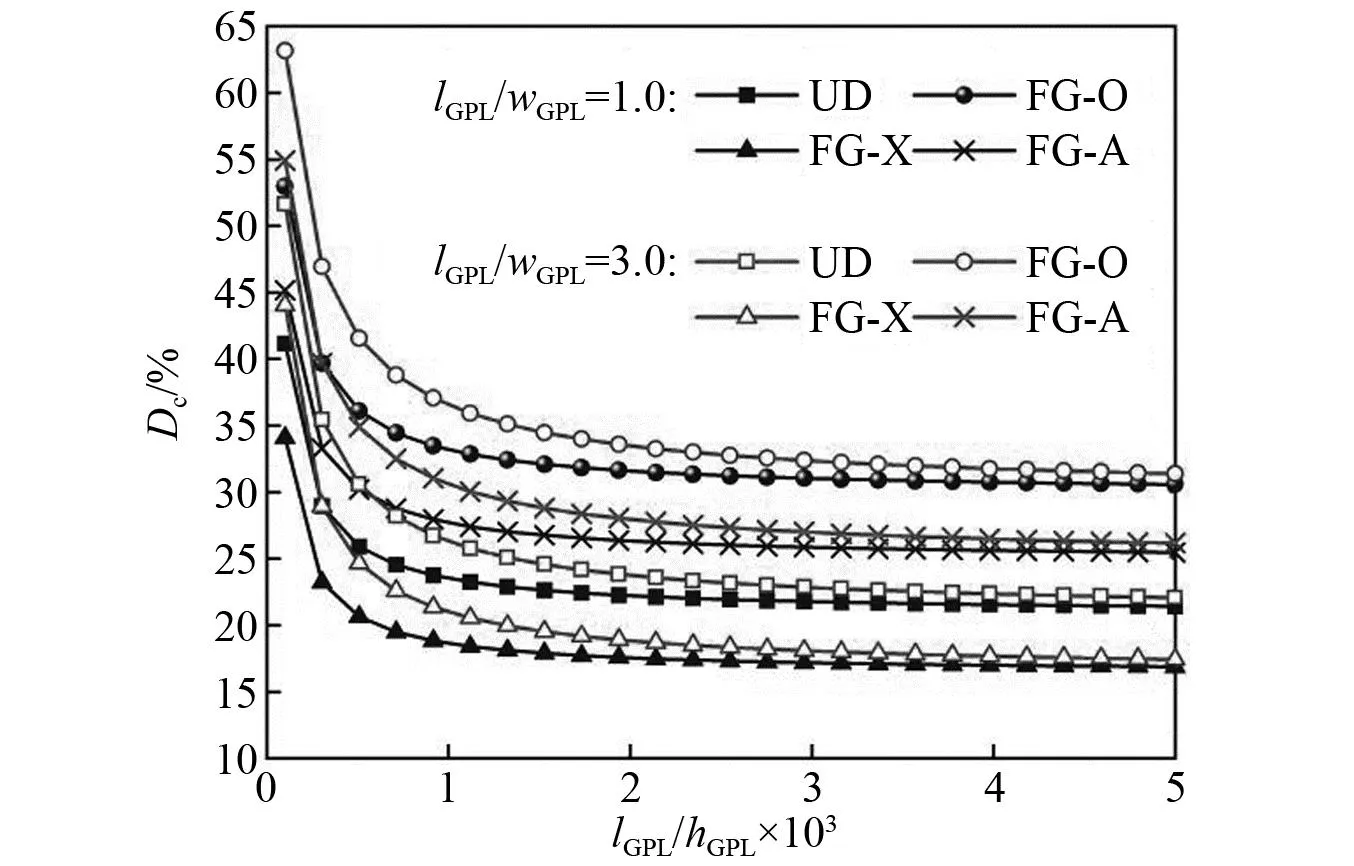
图5 GPLs的几何尺寸对FG-GRC板Dc的影响Fig.5 Effect of gGPL geometry and size on the percentage defection change Dc of the FG-GRC plates

4.3 自振频率分析

下面运用本文方法对FG-GRC板的自振模态问题进行分析和讨论。表4展示了不同宽厚比及GPLs分布模式下四边简支或固支FG-GRC板的前3阶无量纲自振频率,且与Thai等[30]基于广义高阶剪切变形理论,采用等几何分析方法得到的数值结果进行参考比较,说明了本文方法计算FG-GRC板自振频率的准确性。此外还可以发现: 4种分布型下的固支FG-GRC板的自振频率均高于简支FG-GRC板;固定FG-GRC板的宽度,随着厚度h的减少,FG-GRC板结构的自振频率减少。

表4 不同宽厚比下四边简支或固支FG-GRC板的前3阶无量纲自振频率Tab.4 The first three dimensionless natural frequencies of simply supported or clamped FG-GRC plates with different width thickness ratios

图6和图7分析了GPLs的分布模式、总层数NL和质量分数gGPL对FG-GRC板的基频变化率Fc的影响。

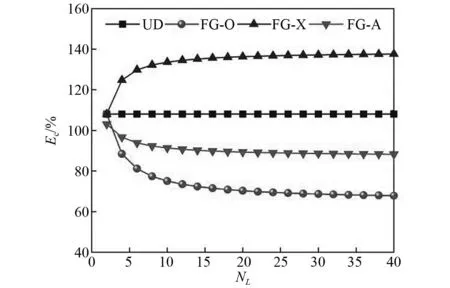
图6 总层数NL对FG-GRC板Fc的影响Fig.6 Effect of total number of layers NL on the percentage frequency change Fc of the FG-GRC plates

图7 gGPL对FG-GRC板Fc的影响Fig.7 Effect of weight fraction gGPL on the percentage frequency change Fc of the FG-GRC plates

定义FG-GRC板的基频变化率为

研究表明:FG-O和FG-A型FG-GRC板的基频随着总层数NL的增加而减少,FG-X型FG-GRC板的基频随着总层数NL的增加而增大,而UD型FG-GRC板的基频随着总层数NL的增加而保持不变;在相同的GPLs质量分数下,FG-X分布模式下的基频最大,FG-O分布模式下的基频最小,这说明在板的顶部和底部界面处分布GPLs,比在板的中面处分布GPLs更加有效增强板的刚度;当FG-GRC板的总层数NL<15～20时,FG-X,FG-A和FG-O分布模式下的板基频变化率较为剧烈,说明该阶段相较于环氧树脂板,GPLs增强板的刚度降低(或增加)较快;当FG-GRC板的总层数NL>15～20时,板基频变化率较为平缓;GPLs的质量分数gGPL从0%逐步增加到1.2%时,FG-GRC板的刚度在增加,从而导致无量纲基频逐渐增大。

图8讨论了GPLs的分布模式、长宽比lGPL/wGPL和长厚比lGPL/hGPL对FG-GRC板的基频变化率Fc的影响。由图8可知,固定GPLs的长度不变,方形GPLs(lGPL/wGPL=1.0)增强FG-GRC板和矩形GPLs(lGPL/wGPL=3.0)增强FG-GRC板的基频均随着长厚比的逐渐增大,GPLs与环氧树脂基体的接触面积逐渐增大,从而结构的整体刚度逐渐增大,导致无量纲基频不断增大,且长厚比在[0,1 000]内时,无量纲基频显著增加。

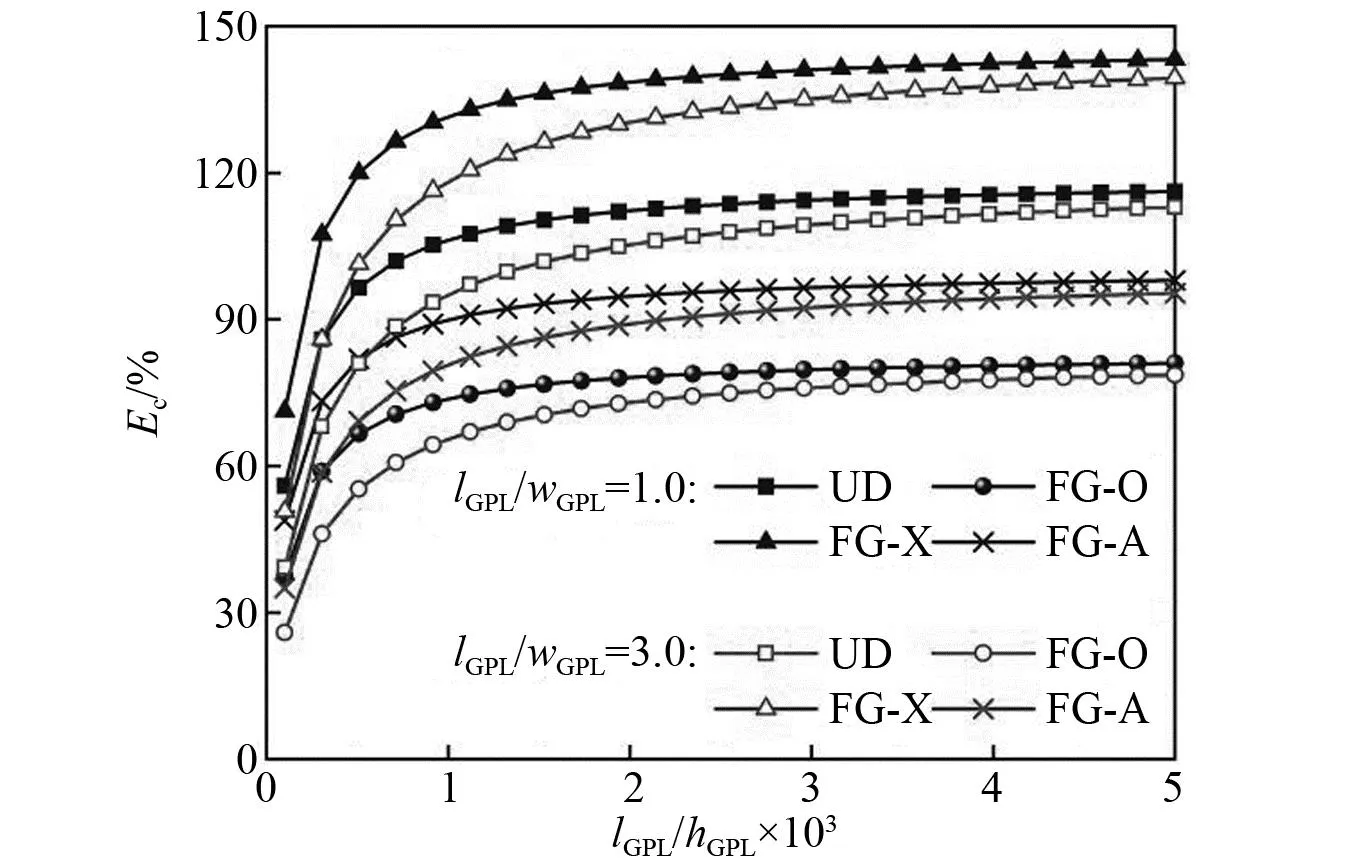
图8 GPLs的几何尺寸对FG-GRC板Fc的影响Fig.8 Effect of gGPL geometry and size on the percentage frequency change Fc of the FG-GRC plates

5 结 论

本文采用基于改进Reddy型三阶剪切变形理论的稳定移动最小二乘近似无网格法求解了功能梯度石墨烯增强复合材料(FG-GRC)板的静态线性弯曲和自振模态问题。通过与文献中解析解的数值结果进行对比,验证了本文方法的收敛性及准确性。数值讨论了GPLs分布模式、几何尺寸、边界条件等对FG-GRC板弯曲和自振模态的影响。研究发现:

(1) 随着边界约束的增强,FG-GRC板的弯曲挠度减少,自振频率增大。

(2) 4种GPL分布模式的增强效果依次为FG-X>UD>FG-A>FG-O。

(3) FG-O和FG-A型FG-GRC板的刚度随着总层数NL的增加而减少,FG-X型FG-GRC板的刚度随着总层数NL的增加而增大,而UD型FG-GRC板的刚度随着总层数NL的增加而基本保持不变。

(4) FG-GRC板中GPLs的质量分数gGPL与板的刚度正相关。

(5) 与无GPLs增强板相比,当FG-GRC板的总层数NL<15～20时,FG-X、FG-A和FG-O型的FG-GRC板刚度变化较为剧烈;当总层数NL>15～20时,FG-GRC板的刚度变化较为平缓。

(6) GPLs长厚比在[0,1 000]内时,FG-GRC板的刚度急剧增加,且方形GPLs(lGPL/wGPL=1.0)增强FG-GRC板的刚度比矩形GPLs(lGPL/wGPL=3.0)增强FG-GRC板刚度大。