基于多头概率稀疏自注意力模型的综合能源系统多元负荷短期预测
韩宝慧,陆玲霞,包哲静,于淼
(浙江大学电气工程学院,杭州市 310027)
0 引 言
随着我国经济的持续发展,能源需求不断增加,能源问题成为影响我国经济可持续发展的关键因素。然而,传统能源系统结构单一,各个能源子系统相互独立,无法有效实现多种能源的协同运行,能源综合利用效率低下。综合能源系统(integrated energy system, IES)突破了传统能源系统的技术和管理壁垒,实现了各类能源的统一规划、管理和调度,在满足多种用能需求的同时提升了能源利用效率[1]。但是随着综合能源系统的不断发展,各能源互补特性增强,多能流间耦合作用加深,大量分布式可再生能源的接入以及电动汽车等新型负荷的出现,进一步加大系统运行不确定性,源网荷之间的多重复杂交互使得系统稳定性受到影响[2]。因此,面对综合能源系统背景下能源供给侧和需求侧的双重不确定性,深入分析和挖掘各个能源子系统之间的耦合特性,实现准确、可靠的多元负荷预测,已经成为当前的重点研究方向[3]。
传统的负荷预测方法主要包括自回归模型[4]、多元线性回归[5]和卡尔曼滤波[6]等统计方法以及随机森林、支持向量机[7]等传统的机器学习方法。近年来,深度学习凭借其对输入输出数据之间非线性特性的准确拟合能力,被广泛应用于负荷预测领域并取得了很好的预测效果。在电力负荷预测方面,文献[8]提出了一种基于长短期记忆(long short term memory, LSTM)网络的短期电力负荷预测模型。文献[9]提出了一种基于完整自适应噪声集成经验模态分解和注意力机制的LSTM预测方法,在LSTM的基础上引入注意力机制以突出关键特征,得到了更好的预测效果。文献[10]基于LSTM的改进网络门控循环单元(gate recurrent unit, GRU)建立预测模型,预测效果相较LSTM网络有所提升。为了进一步提高预测精度,不少学者尝试采用模型融合和模型组合的方式构建负荷预测模型。文献[11]针对电网负荷数据非线性和时序性等特征,提出了一种基于CNN-BiLSTM-Attention深度学习模型实现超短期电力负荷预测,提升了特征提取能力。文献[12]提出基于CNN-LSTM-XGBoost多模型融合的短期负荷预测方法,该组合预测方法相比单一模型预测精度更高。在冷/热负荷预测方面,文献[13]分别采用回归分析、随机森林和神经网络模型对冷热负荷进行预测,证明了神经网络模型的预测效果优于其他2个模型。文献[14]提出一种基于长短期记忆网络的冷负荷预测模型,提升了预测效果。文献[15]使用LSTM预测热负荷,并引入了时空注意机制,提高了热负荷预测的准确性。
目前,针对单一负荷的预测技术已经比较成熟,但是在综合能源系统中,多元负荷不仅受到历史负荷和外部因素的影响,负荷间的耦合关系也会对预测结果产生影响。目前对于多元负荷预测的相关研究相对较少。文献[16]利用多变量相空间重构和卡尔曼滤波对冷热电负荷进行预测;文献[17]针对电-气能源系统建立了基于径向基模型的短期负荷预测;文献[18]提出基于小波包分解和循环神经网络的综合能源系统短期负荷预测方法,使用小波包对冷热电负荷进行频段分解并对各频段内的综合能源负荷进行相关性分析,有效降低了预测误差;文献[19]使用LSTM网络构建了基于冷热电联产系统的负荷预测模型。但是以上文献都采用单任务方式进行负荷预测,针对多能系统的耦合性挖掘力度不够深入。为了进一步挖掘多能系统间的耦合关系,相关学者在多元负荷预测模型的构建中引入了多任务学习。文献[20]建立了基于最小二乘支持向量机和多任务学习的电、热、冷、气负荷组合预测模型,但计算效率较低。文献[21]采用了由多任务学习和CNN-GRU以及集成学习组成的多能负荷预测模型,挖掘了多能负荷的时空相关性。文献[22]提出基于LSTM和多任务学习的综合能源系统多元负荷预测方法,使用硬共享机制结合长短时记忆共享层构建预测模型,提高多元负荷的预测精度。文献[23]采用基于ResNet-LSTM网络和注意力机制的多元负荷预测方法,挖掘多能负荷的空间耦合特性,实现多元负荷的联合预测。文献[24]使用双向GRU结合注意力机制对多元负荷进行未来一小时的预测,验证了多元负荷的预测效果优于单一负荷预测。
作为短期预测的常用方法,LSTM或GRU等都存在一定局限性,如存在梯度爆炸和无法并行运行的缺点。除此之外,大多数多任务架构的实现基本上都基于一个简单的“硬连接”方法,导致要素共享层和具体任务层直接连接,不能反映不同的子任务对共享要素的关注不同。
本文借鉴自然语言处理领域广泛使用的注意力机制,将其改进后应用于多元负荷短期预测,利用多头概率稀疏自注意力(multihead probabilistic sparse self-attention, MPSS)模型学习长序列输入的依赖关系,采用相对位置编码方法增强数据间的内在联系,提高模型的预测性能;并且采用多元预测任务的参数软共享机制,通过不同子任务对共享特征的差异化选择,实现多元负荷的联合预测;最后,在亚利桑那州立大学Tempe校区的多元负荷数据集上对所提模型的性能进行验证。与其他预测模型进行对比,结果表明本文所提多元负荷预测方法能够有效提高预测精度。
1 多元负荷耦合特征挖掘
综合能源系统作为新一代能源系统的重要组成,通过协同发展电、热、冷等多种类型能源,满足不同类型用户的多种用能需求。
一方面,在多元化的电源侧供给互补过程中,风电、光伏、燃气等各类能源供给来源存在着较大的互补特性。同时,综合能源系统集成了电、热、冷等多个能源子系统,在各能源子系统之间均有相互能量转化,充分挖掘了源-源多能耦合、协同互补特性。
另一方面,在综合能源系统的服务商向用户提供多种用能需求的过程中,会受到气象条件、人类活动以及建筑特性等因素影响。气温的变化使得冷热负荷在需求上表现出明显的季节性和地域性,同时,非工作日时居民活动频繁,用能设备灵活多样,用能需求也呈现出随机性和不确定性。
1.1 冷热电负荷相关性分析
本文采用皮尔逊相关系数(Pearson correlation coefficient, PCC)分析多元负荷的内在耦合关系以及多元负荷与气象因素的相关性。皮尔逊相关系数的计算公式为:
(1)
式中:ρY1,Y2为向量Y1、Y2的皮尔逊相关系数;cov(Y1,Y2)为特征向量Y1、Y2的协方差;σY1、σY2分别为Y1、Y2的标准差。
相关系数的取值范围为[-1,1],相关系数的绝对值越大,线性相关性越强。一般认为,相关系数为0.8~1.0表示存在极强相关性,0.6~0.8表示存在强相关性,0.2~0.6表示存在中等相关性,0~0.2表示存在弱相关性或不相关。
使用亚利桑那州立大学Tempe校区的多能负荷数据集,计算综合能源系统多元负荷之间以及与天气影响因素之间的皮尔逊相关系数,得到热力图,如图1所示。由图1可见,电负荷与冷负荷和热负荷之间存在很强的耦合关系,相关系数的绝对值都大于0.6。在多元负荷与天气因素的相关性方面,冷热电负荷与温度的相关性极强,其中冷负荷与温度的相关系数为0.94,热负荷与温度的相关系数为-0.84,这与用户的用能习惯一致,高温时冷负荷需求增加,低温时热负荷需求相应增加。同时,多元负荷与露点、气压、湿度的相关性较强,与风速的相关性比较弱。
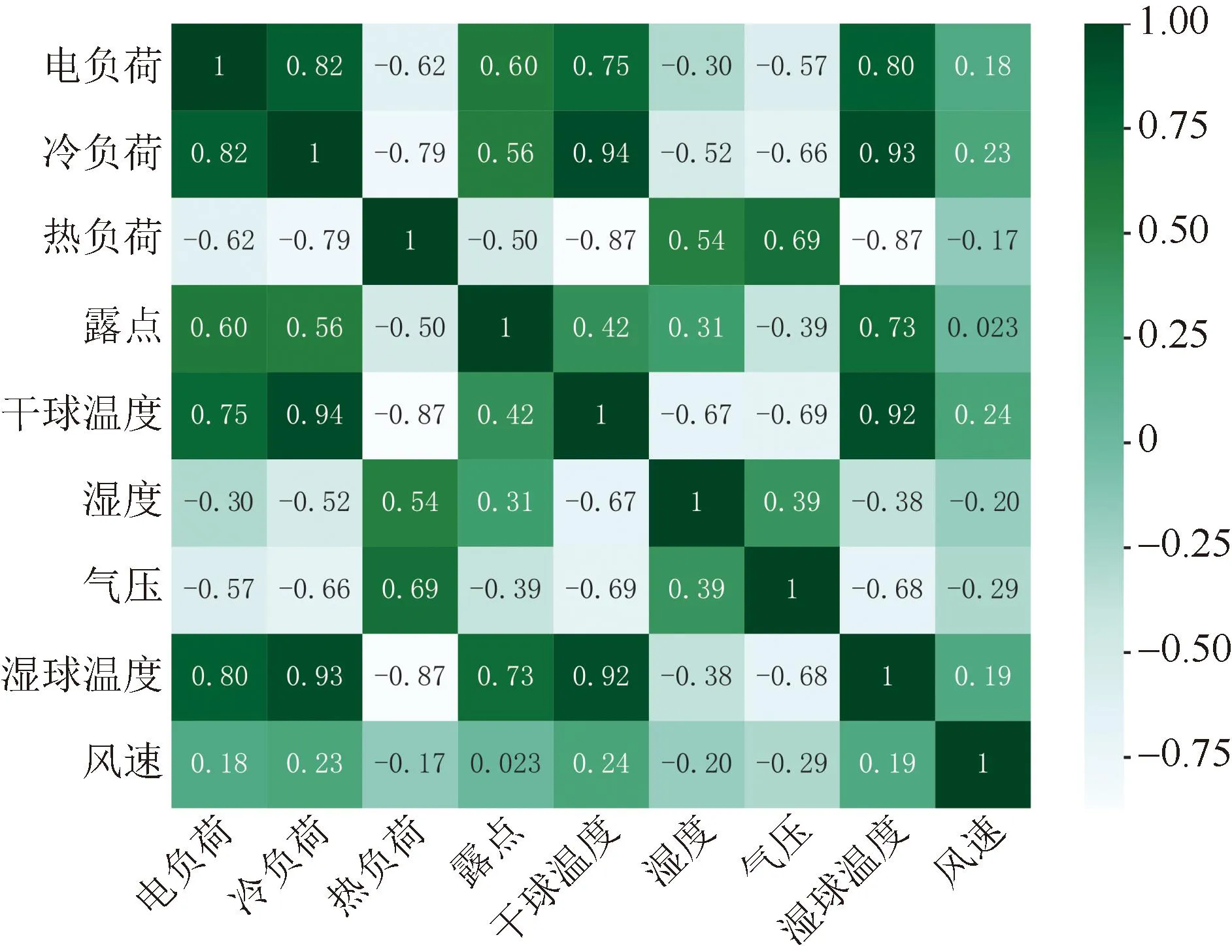
图1 多元负荷的皮尔逊相关系数Fig.1 Pearson correlation coefficient of multi-energy load
由上述分析结果表明,多元负荷之间以及多元负荷与天气因素之间均存在较强的相关性,因此在对多元负荷建模时需要考虑不同负荷之间的耦合性。
1.2 冷热电负荷序列耦合关系挖掘
根据1.1节的结论,可知冷热电负荷之间存在较强的相关关系,但是皮尔逊系数只能对负荷间的线性相关关系进行描述。为了进一步挖掘冷热电负荷之间的非线性耦合关系,针对原始负荷数据,采用取负荷间比值、负荷高次幂和负荷对数的方式对原始数据矩阵进行扩展,以构建原始数据的特征工程。
对负荷进行耦合特征挖掘的算法由以下3个步骤构成。
1)计算原始数据的扩展矩阵。
(2)
(3)
(4)
(5)

2)针对扩展矩阵进行相关性分析。
对于Z1和Z2矩阵,直接采用皮尔逊相关系数分析原始电、冷、热负荷数据与负荷间比值和对数扩展矩阵的相关性。为了避免低相关度数据对预测结果产生负面影响,若原始数据与扩展数据之间的相关度低于0.4,则表示数据间的相关性较弱,此时舍弃该扩展数据,否则保留。
对于Z3矩阵,分别计算负荷内和负荷间的耦合矩阵(以电负荷为例)。
(6)
(7)
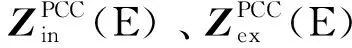
3)计算Z3矩阵的耦合特征。
文献[25]提出了一种基于类似泰勒展开的耦合关系量化方法,计算公式为(以电负荷为例):
(8)
式中:Zb表示电负荷原始数据矩阵(L=1);Zr表示电负荷扩展数据矩阵(L≠1);k=[(1/1!),(1/2!),…,(1/L!)]为建立类泰勒展开所需的系数矩阵;⊙表示哈达玛积。为了避免计算量过大,L取值为3。
最终,获得的耦合特征变量矩阵为:
(9)
式中:F(C)、F(H)分别为经过式(6)-(8)的计算后获得的冷、热负荷的耦合特征。
本文所提耦合特征挖掘算法可以挖掘负荷间的非线性耦合关系,在后续建模中可作为预测模型的输入变量,辅助提高模型的特征提取效果。
2 基于多头概率稀疏自注意力模型的多元负荷预测
编码器-解码器框架是深度学习中一种常用的模型架构,它的主要特点是可以处理长度可变的序列输入和输出。这种模型架构通常用于解决序列转换问题,比如时间序列预测等。本文提出的多头概率稀疏自注意力模型就是基于编码器-解码器框架构建的模型,该模型利用多头注意力机制,实现了不同位置信息的交互和融合,并通过概率分布集中不同的注意力权重,从而实现更加准确的负荷预测。此外,通过引入稀疏性约束,模型的泛化能力和鲁棒性得到了进一步提高。
2.1 多头概率稀疏自注意力模型
1)自注意力模型。
注意力机制来源于人类视觉系统的选择性注意力,当人类观察某一事物时,不会掌握事物的全部细节,而是将注意力放在重点关注的区域,以获取该区域尽可能多的细节。
在深度学习领域中,模型往往需要接收和处理大量的数据,然而在特定的某个时刻,往往只有少部分的某些数据是重要的,这种情况就非常适合采用注意力机制,从大量的信息中选择对当前目标最重要的信息。
自注意力(self-attention)模型[26]是目前注意力模型中使用最广的一种,自注意力模型采用向量点积计算相似度,并采用输入向量维度d对结果进行缩放,然后采用Softmax函数进行归一化计算后得到注意力权重,最后使用注意力权重对值向量进行加权得到注意力分数矩阵,其标准计算公式为:
(10)
式中:A(Q,K,V)为自注意力分数矩阵;Q为查询向量;K为键向量;V为值向量;X为输入向量;Wq、Wk、Wv分别对应Q、K、V向量的可训练的线性变换矩阵;d为输入向量维度。
2)概率稀疏自注意力模型。
在标准的自注意力模型中,每个输入元素都需要关注其他的输入元素,因此得到的注意力矩阵是非常稀疏的。“稀疏”的自注意力结构呈长尾分布,即少数点积对贡献了主要的注意力,而其他点积对产生的贡献则可以忽略不计。因此可以通过删除部分元素之间的连接来降低计算复杂度。
稀疏自注意力模型[27]通过使用Kullback-Leibler散度来进行稀疏性度量,计算得到的度量值大小可以反映对应的查询元素的重要性,度量值计算公式为:
(11)
式中:M(qi,K)为稀疏性度量值;qi为Q中第i个元素;kj为K中第j个元素;LK为K的长度。
基于上述稀疏性度量方法,就可以得到概率稀疏自注意力机制(probability sparse self-attention)的公式,即:
(12)

3)多头自注意力机制。
多头自注意力机制将模型的Q、K、V分出多个分支,形成多个子空间,与稀疏自注意力模型结合后,每个子空间生成不同的稀疏Query-Key对,从而可以让模型关注来自不同位置的子空间的信息,有效避免了信息的损失,计算公式为:
AMH(Q,K,V)=Concat(h1,h2,…,hn)Wo
(13)
(14)
式中:AMH(Q,K,V)为经过多头自注意力计算后的注意力分数矩阵;n为多头的数量,表示对式(12)进行n次计算;Concat(·)为拼接操作;Wo为可训练的线性变换矩阵。
多头注意力机制中,每个头部的线性变换矩阵都是可以训练的参数,因此模型可以自适应地学习每个头部应该关注的序列上下文。此外,多头注意力机制可以通过并行计算多组查询向量、键向量和值向量,从而加速计算,提高模型效率。
2.2 改进位置编码
在时间序列处理任务中,数据间的先后顺序对模型的结果存在显著影响。不同于RNN利用自回归的方式考虑数据之间的顺序,单纯的自注意力模型并未引入结构假设,无法捕获输入元素序列的顺序。因此,为了能够利用输入数据的位置信息,通常采用位置编码的方式生成位置向量矩阵,将位置向量添加到原始输入序列中,即可让输入数据携带位置信息。主流的位置编码方法主要分为绝对位置编码与相对位置编码两大类。
绝对位置编码生成的位置向量矩阵的维度与输入序列维度相同,通过直接相加的方式为每个输入向量添加位置编码,具体公式为:
X=(w1+p1,…,wm+pm)
(15)
式中:X表示经过位置编码后的模型输入向量;wm表示第m个位置的数据嵌入向量;pm表示第m个位置的绝对位置编码向量。
有研究证明[28]在加入未知的线性变化后,使用绝对位置编码方式的模型会丢失原本的相对位置信息,因此本文选择引入相对位置编码。相对位置编码侧重于不同序列之间的位置关系,而不仅是单个序列的位置顺序。对此,在计算Q和K的向量积时引入可训练的辨识相对位置的参数。
采用绝对位置编码的公式为:
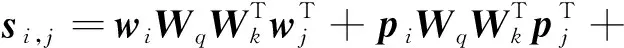
(16)
采用相对位置编码方法改进后的公式为:
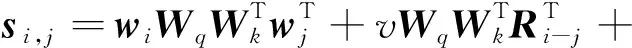
(17)
式中:si,j表示计算Q的第i个元素和K的第j个元素的向量积;Ri-j表示查询向量qi和键向量kj之间的相对位置距离;u、v为2个可训练的参数向量。
2.3 多元负荷预测网络
本文提出的MPSS多元负荷预测网络采用改进位置编码,主要由以下3部分组成:
第一部分为特征提取网络,通过一维卷积层和最大池化层对输入的冷热电历史负荷和耦合特征数据输入序列进行特征提取操作得到特征图,同时进行位置编码,得到相对位置编码矩阵,将特征图与位置编码矩阵组合得到特征矩阵。
第二部分为特征处理网络,通过MPSS网络层进行多头概率稀疏自注意力计算,然后经过蒸馏层提炼重要特征,丢弃冗余特征,提高模型计算效率。多个MPSS网络层和蒸馏层堆叠可以加强特征的多层抽象表示,提高模型的泛化能力。
第三部分为特征映射部分,通过多头自注意力层和全连接层处理后得到冷、热、电负荷的预测结果输出。网络总体框图如图2所示。

图2 多元负荷预测网络框图Fig.2 Diagram of multi-energy loads forecasting model
3 算例分析
3.1 实验设置
本文使用python 3.7作为编程语言,基于PyTorch深度学习框架搭建模型,硬件平台采用Intel(R) Core(TM) i5-10400 CPU@ 2.90 GHz处理器以及NVIDIA RTX 2080显卡。
本文负荷数据来源为亚利桑那州立大学的Campus Metabolism系统,该系统收集了亚利桑那州立大学的所有能耗数据,选择Tempe校区的电、热、冷等历史负荷数据作为负荷预测的数据集[29]。其中,热能值是根据热水进出建筑物时温度和流速的降低来计算的,冷能值是使用水进入和离开建筑物时温度和流速的增加来计算的。为了便于比较和计算,采用kW作为多元负荷的统一量纲,如式(18)所示。
1 kW=3.4 mBtu/h=0.284 RT
(18)
式中:RT为制冷能力的单位,表示每小时的制冷量大小;mBtu/h为制热能力的单位,表示每小时的热量流量。
天气数据来自于美国NOAA气象监测数据网站[30],包括露点、干球温度、湿度、气压、湿球温度和风速信息。日期数据包括工作日、周末和重要节假日数据。
数据集选取2019年1月1日-2019年12月31日之间的冷热电负荷历史数据,其中前80%用于训练模型,后20%用于实际预测。对于训练模型的数据集,按照8∶2划分为训练集和验证集。
3.2 数据预处理
由于数据在采集过程中可能出现异常数据,因此需要进行数据预处理。
首先,采用四分位点内距(inter-quartile range, IQR)检测数据中异常值的基本分布。数据集的四分位数将数据集分为4个部分,每个部分包含25%的数据。计算IQR的公式为:
χIQR=Q3-Q1
(19)
式中:Q1、Q3分别代表第25个百分位数和第75个百分位数。
因此,离群异常值的判定依据为:
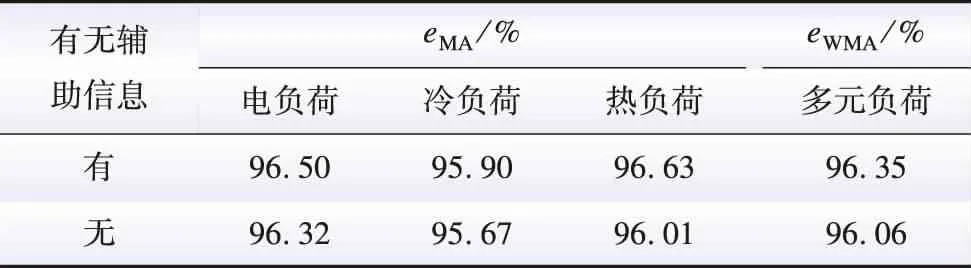
xoutlier=(x>Q3+1.5χIQR)∪(x (20) 式中:xoutlier为离群异常数据;x为原始数据。 然后,异常值作为缺失值处理,消除具有大量缺失值的样本。最后,采用线性插值的方法填补剩余部分的缺失值。 为了加速模型收敛以及消除不同数据量纲之间的影响,使用如式(21)所示标准差标准化(Z-Score)方法对数据进行归一化处理。 (21) 为了全面评估预测性能,本文采用平均精度(mean accuracy,MA)eMA、平均绝对误差(mean absolute error,MAE)eMAE和均方根误差(root mean squared error,RMSE)eRMSE作为每一类负荷的评价指标,采用权重平均精度(weighted mean accuracy,WMA)eWMA作为多元负荷整体的评价指标。针对不同能源的重要性赋予对应的权重,考虑到电力负荷在综合能源负荷中的重要性和不确定性更大,将电、冷、热负荷预测任务的权重分别设置为0.5、0.2、0.3。模型指标的表达式为: (22) (23) (24) eMA=1-eMAPE (25) (26) 综合考虑多元负荷的预测时间和预测精度,本文选择预测时刻前168 h整点的电、冷、热负荷历史数据、计算获得的耦合特征数据以及对应的日期和天气数据作为模型的输入Dinput;选择预测时间段t~t+23的电、冷、热负荷作为模型的输出Doutput。 (27) (28) 超参数调整对于获得最佳预测性能至关重要。但是,对于本文所提出模型来说,调整每个候选模型的所有参数非常耗时。因此,本文采用了一些超参数选择的经验法则和实验方法。首先,参考文献[27]确定了超参数的值范围。然后,使用网格搜索方法获取具有较大影响的超参数值。最后,得到了所提模型的超参数,如表1所示。 表1 模型超参数Table 1 The model hyper-parameter 经过多次实验测试,选择批样本数量(batch size)为72,优化器选择具有学习率衰减的Adam优化器,随着训练次数增加学习率不断下降,学习率初始值设定为0.000 1,衰减系数设置为0.5,学习率随着迭代次数衰减变化为: (29) 式中:lr为学习率;niterations为迭代次数。 1)不同模型对比。 将本文所提出的模型与长短期记忆(long short term memory, LSTM)网络、随机森林(random forest,RF)、轻量级梯度提升机(light gradient boosting machine,LGBM)、基于卷积神经网络(convolutional neural networks,CNN)和长短期记忆网络的融合模型(CNN-LSTM)等进行比较。采用经验法设置对比模型的参数与结构,对比模型的超参数设置如表2所示。除了对比模型自身网络参数的设定,其余的数据处理部分包括数据集划分和数据处理部分与MPSS模型保持一致。 表2 对比模型的超参数Table 2 Hyper-parameters of the comparison models 将训练得到的各个模型对多元负荷进行预测,得到多元负荷的MA值、MAE值、RMSE值和WMA值如表3所示。 表3 各模型预测精度对比Table 3 Comparison of prediction accuracy of each model 为了更直观地显示预测结果,选择了未来96 h的预测曲线,如图3、4、5所示。 由表3可以看出,本文提出的MPSS多元预测模型相比于其他模型的预测精度最高,电、冷、热负荷预测精度分别达到96.50%、95.90%、96.35%。从图3、图4和图5中也可以看出,MPSS模型的预测曲线更加接近真实负荷曲线,预测效果最好。这是由于MPSS模型采用了多头自注意力机制,可以针对不同子任务进行差异化的特征提取,并且能够捕获长时间序列之间的依赖,因此与其他模型相比,MPSS模型具有最高的预测精度。 图4 冷负荷预测结果Fig.4 Cold load forecasting results 图5 热负荷预测结果Fig.5 Heat load forecasting results 2)与单一预测比较。 为了验证多元负荷预测对预测精度有提升作用,将其与单一负荷预测进行对比,采用相同的原始数据和处理方式,设置不同的模型输入输出数据格式,进行对比实验,实验得到各模型精度如表4所示。 表4 单一负荷输入与多元负荷输入的预测精度对比Table 4 Comparison of prediction accuracy between single load input and multiple load input 模型1:模型的输入包括历史多元负荷数据、耦合系数、历史环境特征;模型的输出为多元负荷的预测值。 模型2:模型的输入包括历史单一负荷数据、历史环境特征;模型的输出为单一负荷的预测值。 模型3:模型的输入包括历史多元负荷数据、耦合系数、历史环境特征;模型的输出为电负荷的预测值。 模型4:模型的输入包括历史多元负荷数据、耦合系数、历史环境特征;模型的输出为热负荷的预测值。 模型5:模型的输入包括历史多元负荷数据、耦合系数、历史环境特征;模型的输出为冷负荷的预测值。 由表4可以看出,多元负荷预测相较于单一负荷预测精度分别提高了0.63%、2.01%、1.03%,这说明多元负荷预测包含更多的负荷之间相关性信息,输入特征信息的增多使得模型预测精度更高。同时,本文所提的多元负荷预测模型得到的电负荷、冷负荷和热负荷预测精度与单独训练3个模型的预测结果一致,但是本模型具备同时输出3种多元负荷的预测结果的能力,从而减小了模型训练中的计算开销,提高了训练的效率,具有更高的工程应用价值。 3)辅助信息验证。 由多元负荷和天气数据之间的相关性分析可知,天气信息是负荷预测问题非常重要的辅助信息,对用户的用能行为有直接的影响。同时,节假日和工作日等时间信息也会影响用户的用能需求。因此,为了验证辅助信息对多元负荷预测的提升效果,设置有辅助信息和无辅助信息作为输入的对比实验,得到的结果如表5所示。 表5 有无辅助信息的预测精度对比Table 5 Comparison of prediction accuracy with and without auxiliary information 由表5可以看出,有辅助信息的多元负荷预测精度比没有辅助信息的预测精度更高,说明天气信息和时间信息可以有效提高负荷预测的准确性。 本文针对综合能源系统多元负荷预测问题,在考虑多元负荷耦合特性的前提下,结合深度学习和注意力机制,提出了基于改进位置编码的MPSS模型的多元负荷短期预测方法,有效提升了预测精度。通过选取多个不同预测模型作为对比模型,在真实数据集上验证了所提模型的有效性,并且得到以下结论: 1)综合能源系统与单一能源系统不同,多个能源设备之间相互耦合,多元负荷之间的联系更加紧密,因此多元负荷预测技术应该充分考虑多元负荷之间的耦合特性,才能提升多元负荷的预测效率。 2)与单一负荷预测相比,考虑外界因素以及多元负荷特征的预测精度更高。因此,在进行综合能源负荷预测时,考虑负荷之间以及负荷与外界因素之间的相关性能够有效提升预测精度。 3)本文提出的基于改进位置编码的MPSS模型的多元负荷短期预测方法充分考虑了多元负荷的耦合特性和输入输出数据之间的长期依赖关系,通过仿真实验以及与LSTM、RF、LGBM、CNN-LSTM等模型进行对比,验证了本文所提模型比其他模型具有更高的预测精度。
3.3 实验评价指标
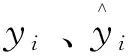
3.4 模型输入输出数据
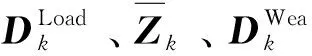
3.5 模型超参数设置

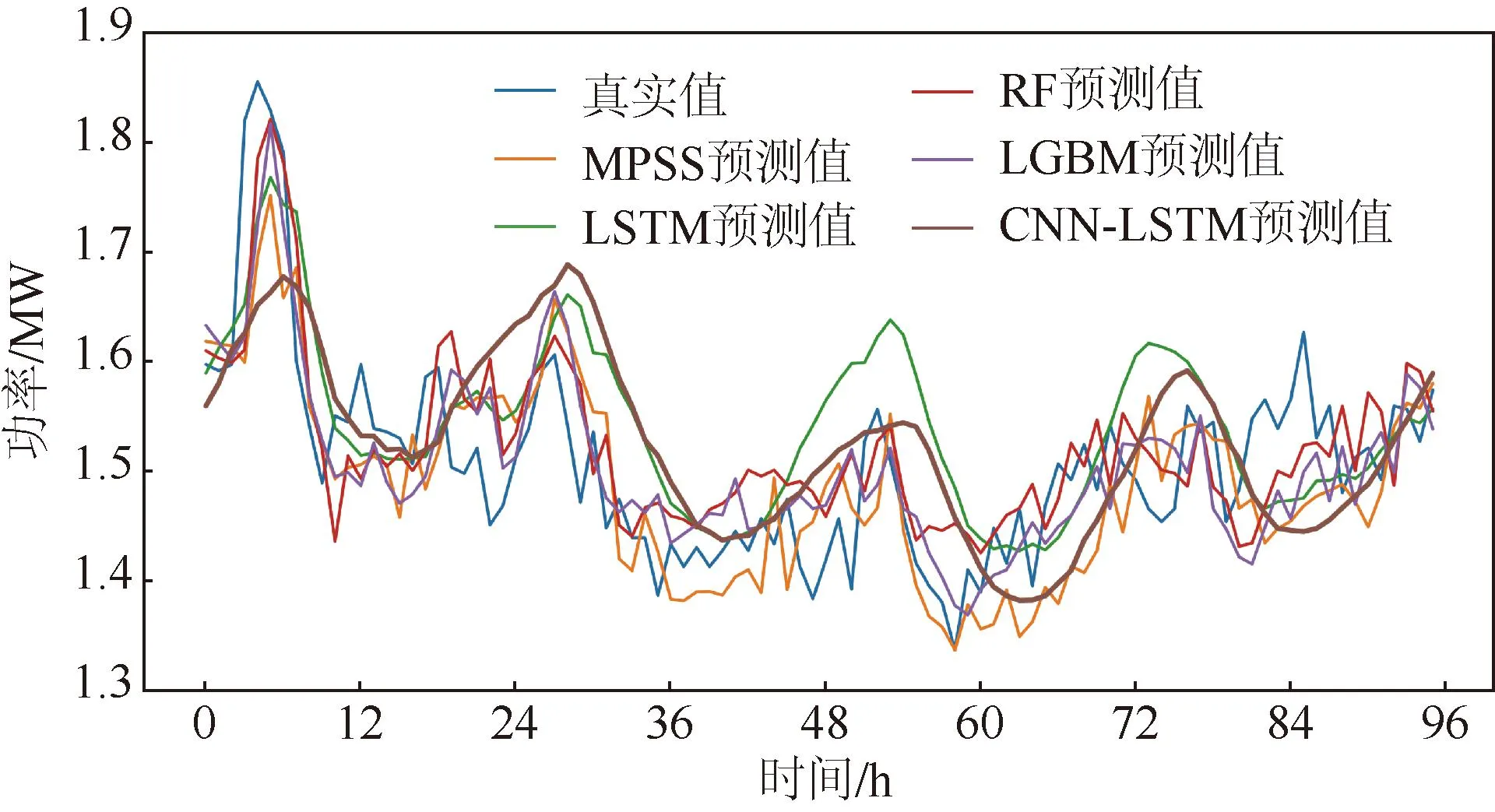
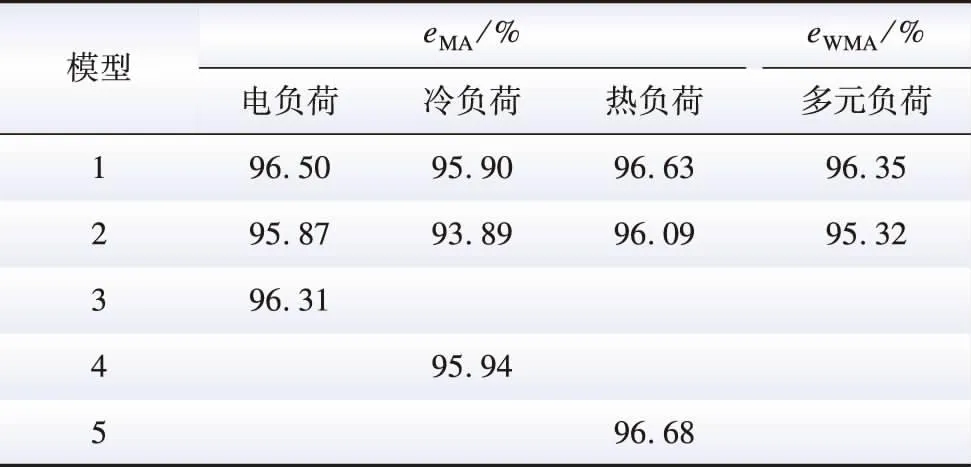
3.6 结果分析



4 结 论

