电力市场环境下源-网-荷多主体协调互动规划

康一鸣,秦文萍,姚宏民,邢亚虹,胡迎迎,贾杏平

(1. 国网山西省电力公司营销服务中心,太原市 030032;2.太原理工大学电气与动力工程学院, 太原市 030600;3.国网山西省电力公司经济技术研究院,太原市 030000)

0 引 言

加快建设全国统一的电力市场体系是对未来多年我国电力市场改革的重要部署和构建新型电力系统的重要举措[1-3]。新型电力系统规划作为引领电力系统绿色低碳发展及电力市场改革的重要技术前提[4-5],在完成传统规划的同时,还需统筹考虑源-荷强不确定性、各利益主体与电力市场的耦合性对规划的影响。

电力市场是建设新型电力系统、实现“双碳”目标的基础市场[6]。因此,探讨在售电侧以及增量配电网放开前提下的源-网-荷集成互补,协调配电网的发展,满足市场化改革条件下的持续可靠供电是配电网规划设计工作中必须加以考量的重要因素[7]。已有不少学者在规划中考虑电力市场的影响。文献[8]建立售电市场环境下的配电网双层规划模型,上层模型确定网架初始规划方案,下层模型将配电网运营商的盈利来源分为直接售电收入和向售电公司收取的过网费,以其利益最大为目标函数,确定日最优调度方案。最后通过算例仿真表明,在开放售电环境下,配电网运营商在降低网架投资运维成本的同时,还应提升服务质量以适应激烈的市场竞争。文献[9]针对电力市场价格的不确定性,提出一种基于场景驱动的多阶段决策规划模型。模型首先确定规划期内电力批发市场场景,以电网总成本最小为目标函数完成电网设施配置和容量的初始决策,然后在零售用户的竞价空间上寻找满足可靠性的最优供电场景,通过迭代得到最终规划方案。然而,现有研究考虑电力市场影响的规划往往从配电网运营商的角度出发,缺乏对该环境下涌现的其他市场主体的考量。

在配电网规划领域,随着以分布式电源(distributed generation, DG)为代表的拥有合法售电资质的用户侧新型主体大量涌现,对配电网各主体单独规划的规划方法已经无法适应新型电力系统复杂多变的互动响应关系[10-13]。因此,在配电网规划时,需要设计更合理的规划方案,力求保证配电网运营商投资经济性的同时,兼顾系统中各主体的利益。文献[14]针对分布式发电在不同阶段可能存在的不同分布式电源投资主体,即配电运营商和用户,分别建立DG优化配置模型;文献[15]提出一种兼顾配电网运营商、DG运营商和用户三者利益的主动配电网三层规划模型,通过将规划变量转化为层间传递介质的方式保证求解结果的有效性。上述文献虽然考虑了不同主体的利益,但是在建模时弱化了电力市场对规划结果的影响。

多主体规划是一个多目标优化问题,求解难度较大[16],大部分研究均通过单目标转化法实现问题的简化。文献[17]分别建立各主体优化模型,求解时通过线性加权法将多目标函数转化为单目标函数;文献[18]采用优劣解距离法,将源、网、荷三个不同的目标函数变为单目标函数。上述求解方法虽然降低了求解难度,但是求解过程带有一定的主观性,且各个主体的利益存在冲突,与实际情况大相径庭。

综上,现阶段的配电网规划研究中,普遍缺乏对各利益主体与市场耦合关系的考虑。在此背景下,本文首先分析了电力市场对源、网、荷三者的影响,在此基础上,提出一种基于博弈论的源-网-荷多主体协调互动的规划模型,并通过迭代搜索法和改进的粒子群算法(particle swarm optimization, PSO)对模型进行求解。最后,通过改进的IEEE 33节点与实际9节点系统算例与实际9节点系统,验证所提模型的可行性与有效性,为电力市场开放环境下多决策主体利益博弈的规划问题提供思路和建议。

1 配电网中各主体的市场关系分析

峰谷电价机制是在传统管制下负荷管理的产物[19]。这种电价机制在时空上均无法满足新型配电系统的需求:从时间上看,由于其时段固定,难以适应新能源的波动性[20-21];从空间上看,缺乏对资源稀缺地域性的考量,与阻塞管理相关度小。在此背景下,分析现行电力市场电价机制,激励并引导用户积极参与市场交易,对消纳新能源、缓解电网阻塞具有重要意义。

电力交易是一个不断选择的过程,在哪个交易批次交易成本最小是电力用户做交易策略的逻辑。现行电力市场规则中,中长期合同受很多市场规则、市场环境参数的影响,主要包含年、多月、月、旬等多个品种。在本文中,配电网规划中的利益主体主要包括DG运营商、配电网运营商及电力用户,源-网-荷各主体的市场关系如图1所示。为降低计算量、剔除低相关度变量,在图中对市场环境参数进行了简化与假设。

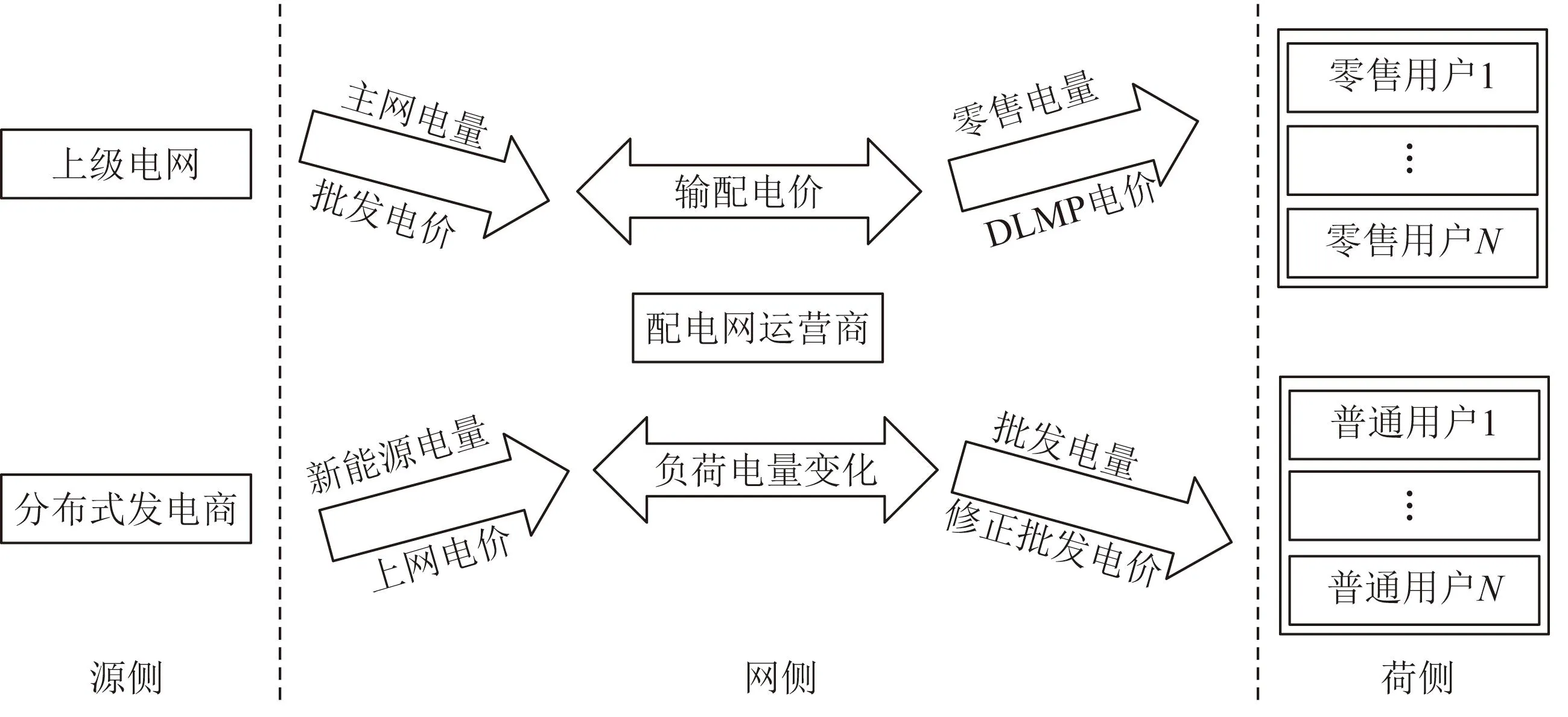
图1 配电网中源-网-荷各主体的市场关系Fig.1 The market relationship of source-network-load in distribution network

DG运营商以上网电价将电量卖给配电网运营商或者用户获得收益。配电网运营商从上级电网或者DG运营商处购电,若参与传统电力市场交易,其收益为用户占用输配电线路而支付的输配电价[22]。若参与分布式发电市场化交易,收益则为“过网费”,是源-荷所处电压等级输配电价的差值[23]。

假设用户侧所有用户均参与电力市场,且均为零售商,当其与配电网交易时,会形成统一的零售电价。本文采用节点边际电价(distribution locational marginal price,DLMP)描述这种在零售交易时形成的零售电价。文献[24]中证明在统一价格出清模式下,DLMP 与零售商的购电量呈现强线性相关性,因此,引入一次函数描述DLMP以简化复杂的电力市场出清问题。具体公式如下:

(1)

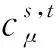
2 源-网-荷主体博弈关系分析

博弈是指若干决策主体,在一定的约束条件下,依靠自身掌握的信息,一次或者多次选择最优策略,最终取得最佳收益的过程。一个博弈格局通常由参与者、策略、支付(收益)及均衡四个要素构成[25-27],表1所示为各要素的定义。

表1 博弈要素的定义Table 1 Definition of game elements

在电力市场环境下,DG运营商等主体并存地追求各自利益最大化,构成多个主体的博弈关系。其中DG运营商、配电网运营商要在掌握彼此全部策略信息的基础上,制定满足各自利益的规划方案。因此,这两个主体间的博弈格局为完全信息静态的非合作博弈[28]。而电力用户在追求自身利益时不会受到配电网规划结果的直接影响,在本文中不被视为博弈的参与者[29]。

DG运营商、配电网运营商的博弈策略在优化模型中体现为各自的决策变量,分别记作DG待接入节点XD、DG安装数量N以及待建线路XG。其策略空间受到经济、政策等因素的影响,表述为式(2)和式(3):

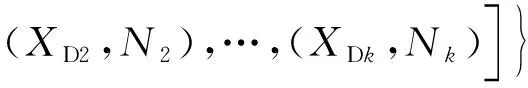
(2)

XG∈{QG=[XG1,XG2,…,XGp]}

(3)

式中:QD、QG分别表示两者的策略空间;(XDk,Nk)表示DG的第k种规划策略;XGp表示线路的第p种规划策略。显然策略空间是有限的,由表1可知,该博弈必然至少存在一个Nash均衡解。

DG运营商、配电网运营商的收益函数CD、CG分别为各自规划模型中的目标函数,计算公式详见第4节。

3 基于用户效用的需求侧响应模型

本文使用基于用户效用的需求侧响应模型[21]表征电价等环境变量对电能需求的影响情况。电力用户的效用可定义[30-31]为:用户通过消费电能而获得的心理满足感,而效用函数Φ[P(t)+B(t)]则是描述两者之间定量关系的函数。本文使用文献[32]所提的二次效用函数,它具有非减且边际效益非增的特性[33]:

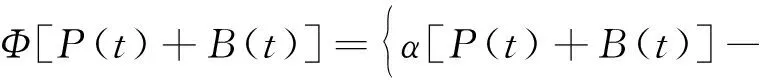
(4)

式中:P(t)、B(t)分别为第t时刻需求侧响应负荷以及原负荷;α、β为衡量用户单位效应函数的时变系数。实际上,时变系数反映的是环境变量对电力需求的影响,因此,通过改变其值的大小可以捕捉到用户需求的动态变化。

4 源-网-荷协调互动的规划模型

4.1 模型概述

本文所述模型由博弈层和模拟层构成。博弈层基于斯塔克尔伯格博弈理论,建立源-网规划模型。其中源侧以最大化DG运营商的收益为目标,以DG接入位置、数量以及容量为决策变量;网侧以最小化配电网运营商年综合值为目标,以网架结构为决策变量。模拟层考虑第1节所述源-网-荷多主体电价互动关系,建立荷侧规划模型。荷侧以最大化用户收益为目标,以需求侧响应电量为决策变量,各主体协调互动关系如图2所示。

图2 源-网-荷协调互动规划模型关系图Fig.2 Source-network-load coordinated interactive planning model diagram

4.2 源侧模型

4.2.1 目标函数

源侧模型以最大化DG运营商收益为目标函数,如式(5)所示,确定分布式电源的位置和数量。

(5)

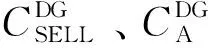
各成本费用计算公式如下:

(6)

(7)

DG运营商投资成本如式(8)所示。

(8)

(9)

DG运营商运维成本如式(10)所示。

(10)

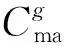
4.2.2 约束条件

1)分布式电源约束。

(11)

(12)

(13)

2)网损减少约束。

当配电网接入DG后可能会使系统网损增加,因此,为了提升系统整体经济性,需要设置式(14)所示的网损减少约束。

(14)

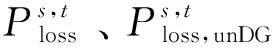
4.3 网侧模型

4.3.1 目标函数

网侧以最小化配电网运营商年综合值为目标函数。

(15)

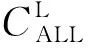
(16)

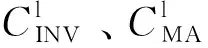
(17)

(18)

(19)

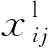
2)配电网运营商的网损CLOSS。

(20)

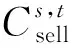
3)配电网运营商的故障成本CFAIL。

(21)

(22)

4)配电网运营商的碳排放成本CCO2。

(23)

5)实施需求侧响应项目的管理费用CDR。

(24)

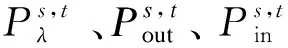
(25)

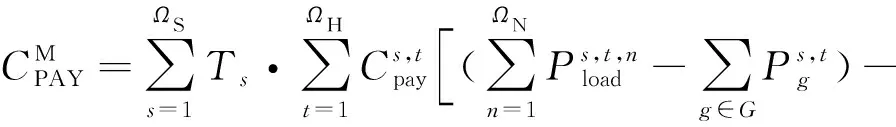
(26)

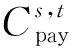
4.3.2 约束条件

1)支路潮流约束。

(27)

2)安全约束。

(28)

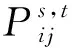
4.4 用户侧模型

4.4.1 目标函数

根据文献[34],定义在一个时间周期中用户效用与用户支付的差值为用户收益。

(29)

式中:Φκ、Φλ分别为用户参与可转移负荷、可中断负荷的效用函数;Φn为普通用户的效用函数;ΩTL、ΩIL分别为可转移负荷、可中断负荷的节点集合;ΩO为普通负荷的集合。

各收益计算公式如下:

1)用户参与可转移负荷响应的负荷效用Φκ。

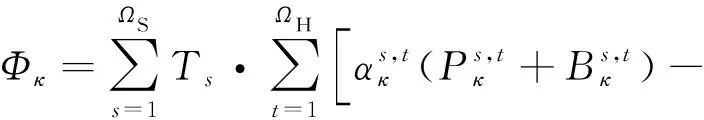
(30)

2)可中断负荷效用Φλ。

用户参与可中断负荷的负荷效用可以看做是特殊的可转移负荷响应的效用,故效用函数如下:

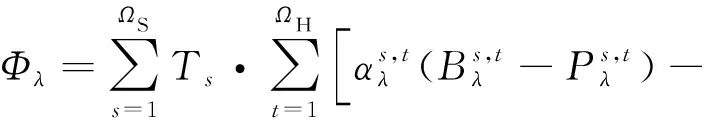
(31)

3)普通用户效用Φn。

本文定义Φn为用户在时间t内得到的效用,用以表征消耗的电能为用户带来的实用价值。

(32)

4)用户的购电费用CBUY。

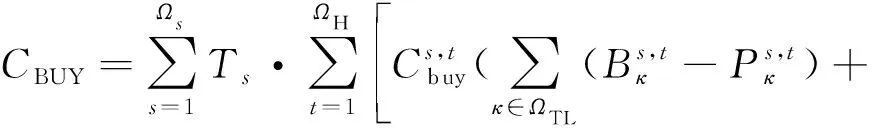
(33)

4.4.2 约束条件

1)需求侧响应运行约束。

(34)

(35)

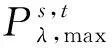
5 模型求解

由第2节可知,博弈优化问题并不是一个整体优化问题,实际上每个参与者都要独自优化以达到各自利益最大化。对本文所提优化模型,采用基于粒子群算法的迭代搜索法求解均衡点[34],具体求解流程如图3所示,详细步骤如下:

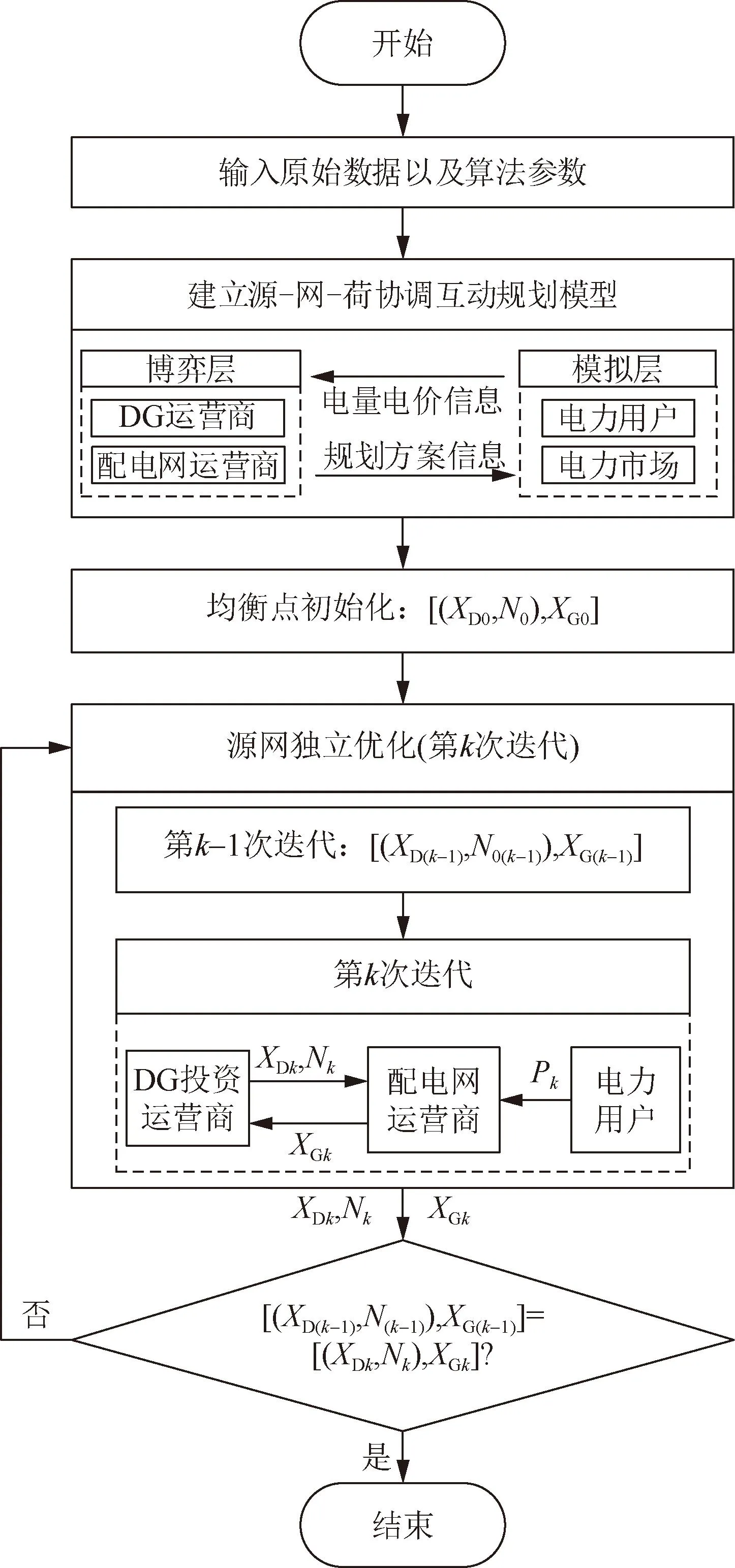
图3 博弈模型求解流程图Fig.3 Game model solving flow chart

1)输入数据与算法参数。清洗原始数据:剔除重复值异常值,并通过机器学习方法预测数据中的缺失值;输入数据处理后的新能源出力参数、相关负荷数据以及日前市场电价参数;采用场景分析法生成场景,确定PSO算法的相关算法参数。

2)建立博弈模型。按照第4节模型设计思路,建立源-网-荷协调互动规划模型。

3)平衡点初始化。分别在DG运营商、配电网运营商各自策略空间中随机选取一组值(XD0,N0)、XG0作为迭代初始值。

4)源-网独立优化。记博弈中各参与者第k轮优化结果为(XDk,Nk)、XGk,具体的,在第k轮优化时,各参与者根据上一轮优化结果(XD(k-1),N(k-1))、XG(k-1),通过PSO得到最优的策略组合(XDk,Nk)、XGk,此时应当满足:

(36)

(37)

基于PSO的优化流程参考文献[4]。在优化前,按照文献[24]所提DLMP的求解方法拟合每个时间断面的DLMP函数,并结合购电量得到各个时刻的DLMP后,再进行后续计算。

5)判断是否找到Nash均衡点。若各个博弈者相邻两次得到的最优解相同,即:

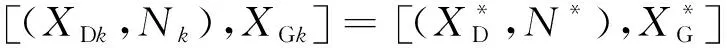
(38)

则表明博弈达到平衡点,在该博弈中的任何参与者都不能独立优化获得更多的收益,博弈优化达到Nash均衡;反之,若没有达到Nash均衡,则返回步骤4)。

6 算例分析

6.1 测试算例分析

6.1.1 参数设置

为验证本文所提协调互动模型的有效性,首先采用改进的IEEE 33节点系统进行算例仿真。仿真参数如表2所示。

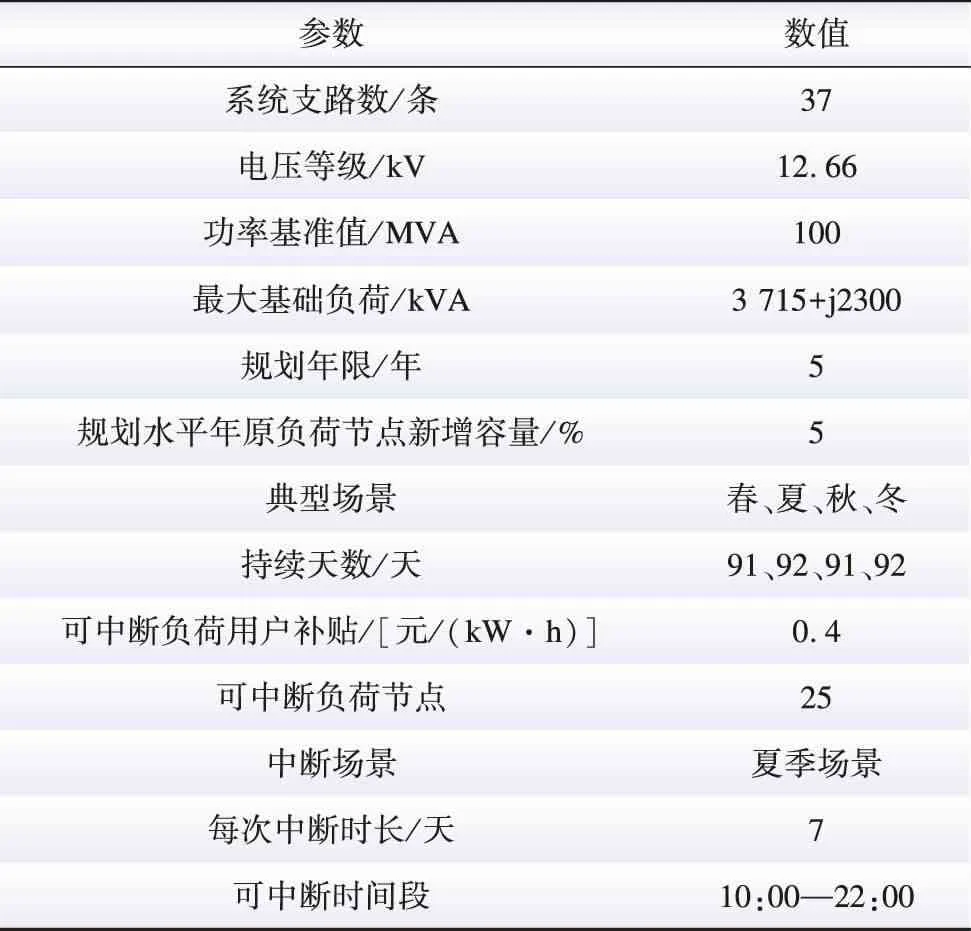
表2 仿真参数Table 2 Simulation parameters

DG考虑风电、光伏发电,DG相关数据来源于文献[4],DG与线路拟规划位置如图4所示,节点34-37为新增负荷节点,虚线为待选新建线路。新增负荷节点以及线路数据详见文献[8],典型光伏、风电以及负荷出力的时序特性详见文献[2]。

图4 IEEE 33节点配网Fig.4 IEEE 33-node distribution network

本文所提日前价格采用某地批发市场一季度分时段限价的参考价[35],峰谷电价数据、峰谷平时段划分见文献[4],电价变化曲线如图5所示。

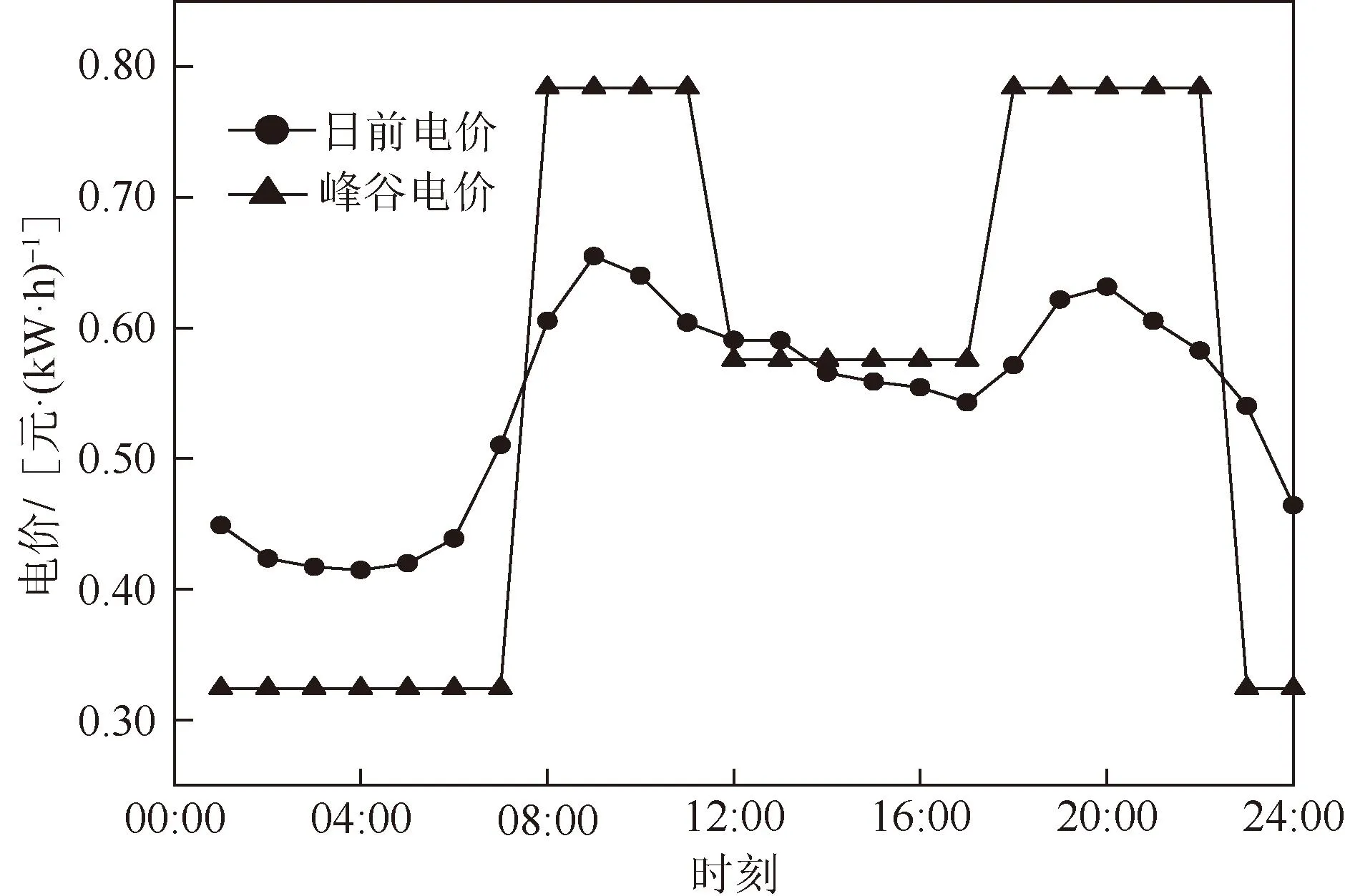
图5 电价变化曲线Fig.5 Electricity price change curve

6.1.2 不同电价机制对需求侧响应的影响分析

由第1节可知,本文通过电价机制以夏季场景为例,使用第4.3节所提用户侧模型实现典型日用户负荷调度模拟,得到某用户在不同电价机制下的需求侧响应负荷曲线,如图6所示。

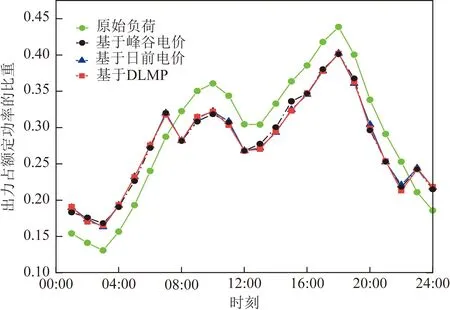
图6 典型日负荷曲线比较图Fig.6 Comparison chart of typical daily load curve

由图6可知,在引入基于峰谷电价的需求侧响应时,00:00-7:00为电价谷时段,用户通过增加用电获得峰谷价差收益。在12:00-17:00时,用户结合自身满意度以及电费支出情况,通过负荷中断获得可中断负荷补贴。在08:00-11:00、17:00-23:00时,用户通过减少用电减少峰时电费支出。

对比图5、图6可知,在不同电价机制下,电价曲线变化较大,而负荷曲线变化较小,这是因为峰谷段需求侧响应电量均达到最大值。在13:00-17:00时,日前电价下的负荷均略低于峰谷电价下的负荷,这说明在峰谷电价的平时段引入日前电价机制,能提高用户响应的积极性。

表3为典型日三种电价机制下DR管理费用以及用户的购电费用的变化情况。根据第4节所述模型,使用日前电价时,DR管理费用更高,需求侧响应电量更大,用户响应更积极。同时,表2也表明使用日前电价时,用户会减少购电,通过改变用电习惯获得收益,表明电力市场对需求侧响应的增益作用。

表3 典型日某节点费用情况Table 3 The bus cost situation of the typical day 元

由表3可知,使用DLMP时, DR管理费用以及用户购电费用均高于使用日前电价时的费用,这是因为DLMP具有的边际递增效应使其电价略高于日前电价。

6.1.3 规划结果分析

1)源-网-荷协调互动模型的有效性分析。

为验证本文所提模型的有效性,设计以下三种情形并进行仿真验证。

情形1：不考虑源-网-荷博弈关系,各主体独立优化;

情形2：使用文献[4]所提双层模型,DG运营商与配电网运营商整体优化;

情形3：考虑源-网-荷博弈关系,使用本文所提源-网-荷协调互动模型。

3种情形下得到的规划结果见表4,表中给出3种情形下配电网规划方案,表中三种情形下光伏的安装数量普遍低于风电安装数量,这是因为光伏夜晚出力为0,出力变化过大,容易产生供电缺口。

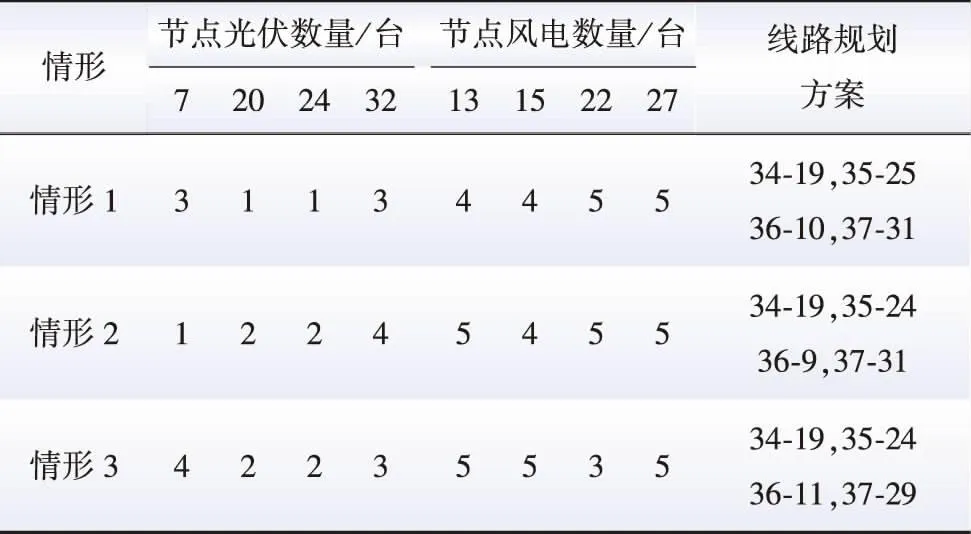
表4 不同规划模型的规划结果Table 4 The planning results of different planning models

各情形下DG运营商的投资如表5所示。由表5可知,情形1、2、3中DG 运营商的各项成本以及收益依次递增,DG安装总数按照三种情形的顺序依次为26、28、29。

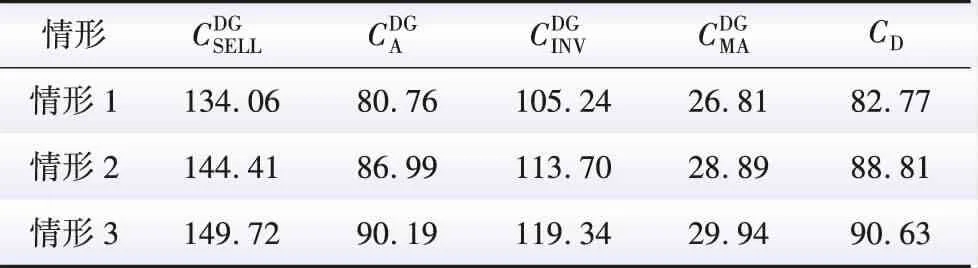
表5 DG运营商费用Table 5 DG investment operator fees 万元

出现这种规划结果的原因是,在考虑源-网整体利益后,能够激发源-网整体与用户侧的互动响应,进而提升需求侧响应能力,促进新能源消纳;在考虑源-网-荷协调互动响应后,DG的并网容量进一步增加,使得投资成本增加,同时,DG出力的增加使得各项成本收益均增加。

表6为三种情形下配电网运营商的年化成本变化情况。情形2、3与情形1相比,虽然需求侧管理费用略有增加,但是网损成本、线路投资成本、碳排放惩罚费用均降低。这说明当考虑源-网共同利益或者源-网主体博弈时,能够进一步挖掘用户的需求侧响应潜力,积极响应电价变化,进而达到延缓线路投资的目的。同时,情形2、3中故障成本以及向主网的购电成本均降低,这说明当考虑源-网共同利益或者源-网主体博弈时,均可使DG出力增加,使得故障时可供电量增多,电量不足期望值减少。此外,由于电网中总负荷需求一致,因此DG出力的增加势必导致主网购电的减少。

表6 配电网运营商费用Table 6 Distribution network operator fees 万元

情形2与情形3相比,情形3之所以线路投资费用增加,是因为DG运营商和配电网运营商通过博弈追求各自利益最大化,配电网运营商需要牺牲一部分自身的利益以保证DG运营商的利益,因此这种规划方法能够保证各自利益达到均衡,在现行电力市场化交易的大环境下具有较强的适应性。

2)电力市场因素对规划结果的影响分析。

为验证不同电价机制对规划结果的影响,设计以下三种情形并进行仿真验证。

情形4：采用传统峰谷电价的配电网源-网-荷协调互动规划;

情形5：采用日前电价的配电网源-网-荷协调互动规划;

情形6：采用节点边际电价的配电网源-网-荷协调互动规划。

3种情形下得到的规划结果见表7。由表7可知,情形5、情形6的规划结果完全相同。情形4与情形5、6相比,规划结果略有不同:新增DG数量减少1台,同时35负荷节点的连接点由24变为25。

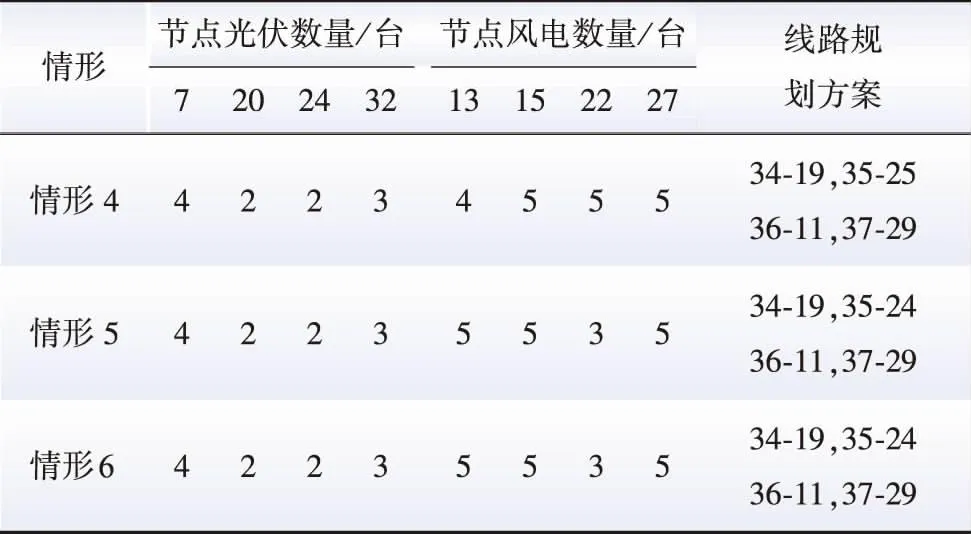
表7 基于不同电价机制的规划结果Table 7 Planning results based on different electricity price mechanisms

图7为配电网运营商费用情况。在情形4中主网购电费用较情形5、6高,这是因为峰谷电价均值较之日前电价高,从主网的购电费用会相应增大。

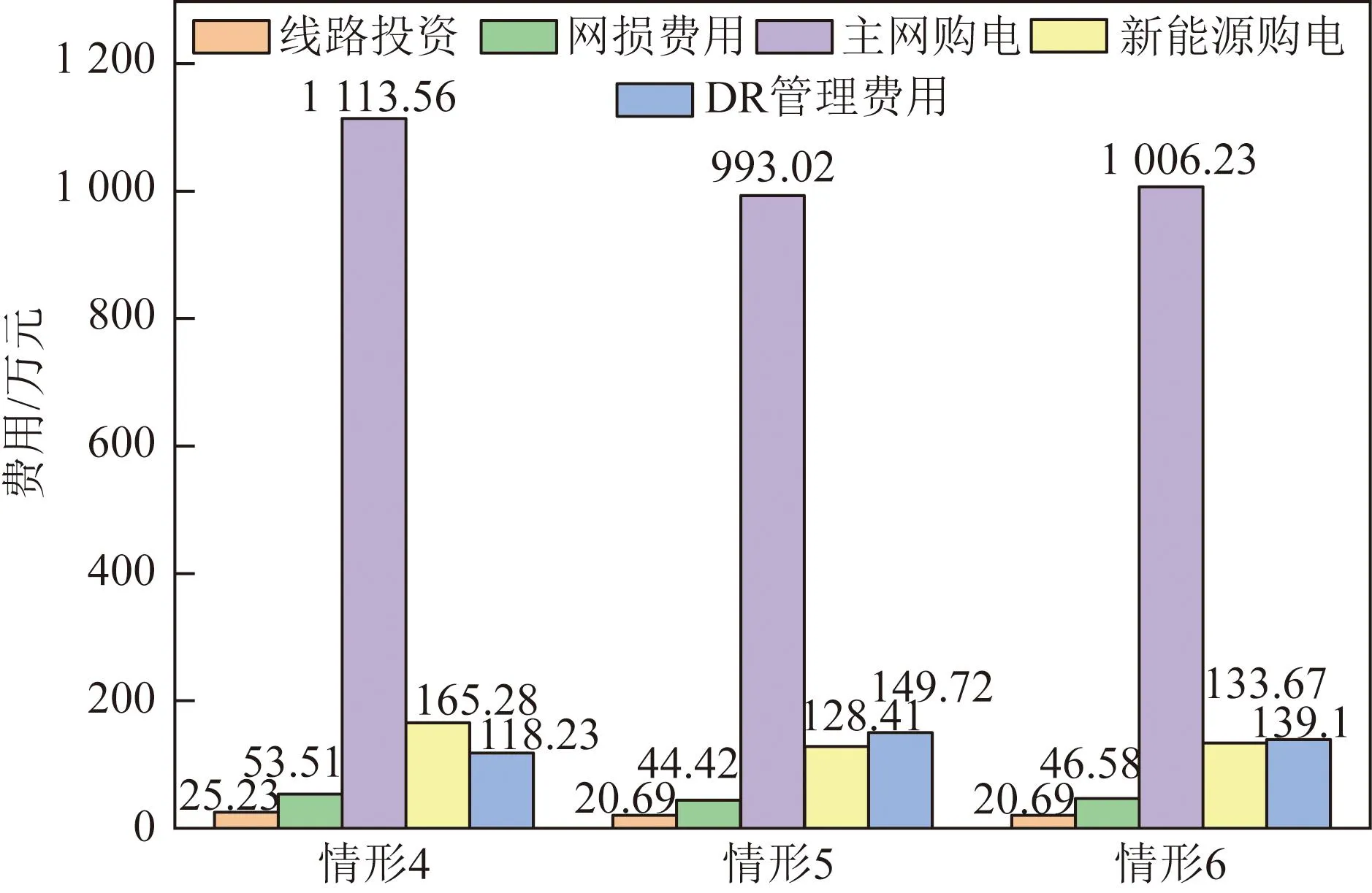
图7 配电网运营商费用变化情况Fig.7 The fees changes of distribution network operator

由此可见,当引入市场电价机制后,配电网运营商花费降低,体现了市场因素的积极作用。情形5、情形6中新能源购电费用、DR管理费均大于情形4,而网损以及线路投资均减小,这说明在考虑市场因素后,能够达到挖掘用户需求侧响应潜力、延缓线路投资的目的。

对比情形5、情形6可知,当使用DLMP后,并不会影响电网的规划结果,但是由于计及配电网中的边际成本递增效应,各项成本费用均提升,但仍小于原峰谷电价时的总费用成本。

6.2 实际算例分析

6.2.1 参数设置

以山西某地10 kV电网为实际算例,验证模型的有效性与实用性。该电网区域平均负荷为1.36 MW,最大负荷为3.54 MW,最大负载率为45%,最大负荷利用小时数为3 285 h。该实际算例的算例节点图如图8所示。各负荷节点参数、运行参数、待接入线路参数详见附录A。新增负荷节点为10、11、12、13,分布式光伏待接入位置为节点2、3、4、5、6,其余参数均与测试算例一致。

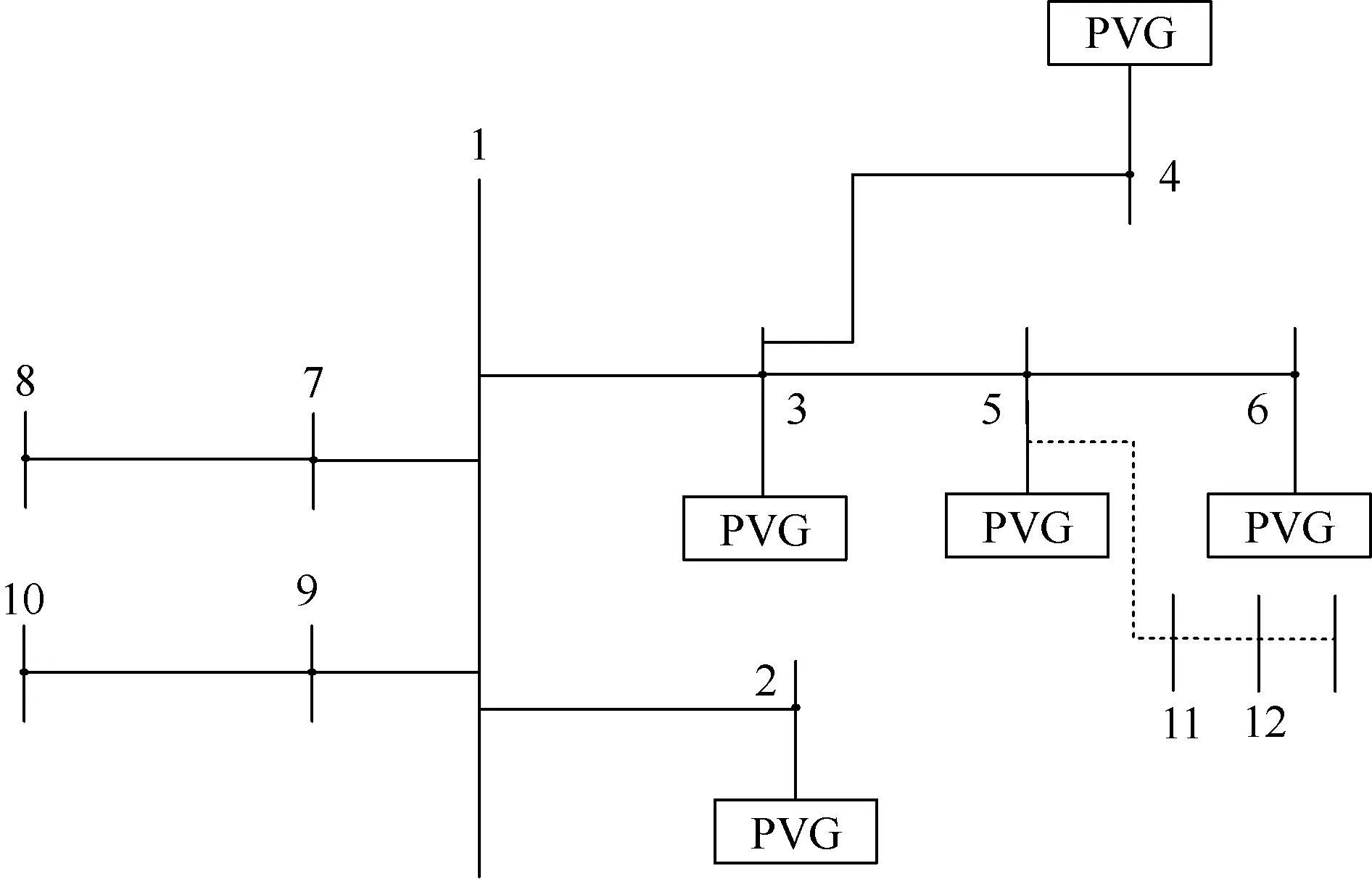
图8 山西省某地9节点配网系统(算例节点图)Fig.8 A 9-bus distribution network system in Shanxi province (example bus diagram)

6.2.2 规划结果分析

1)源-网-荷协调互动模型的有效性分析。

为验证所建模型在实际配电网规划中的有效性,设置如6.1.2节第一部分的三种规划情形并仿真验证。三种情形下得到的规划结果见表8。在该算例中,已确定线路安装位置,故无需再次制定线路规划方案。由表8可知,三种不同规划模型下,光伏的安装数量依次为17、18、20,这说明当考虑源-网两者或者源-网-荷三者利益时,会刺激利益主体增设更多的DG以保证自身获得更高的收益。

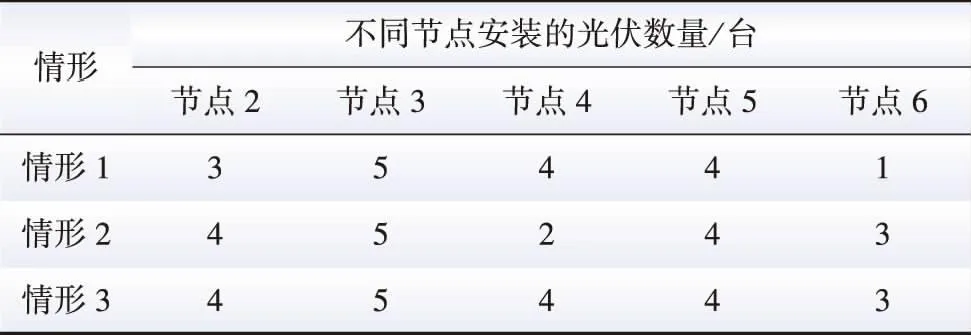
表8 9节点实际配网系统使用不同规划模型的规划结果Table 8 The planning results of different planning models in the 9-bus actual distribution network system

各情形下DG运营商的投资情况如表9所示。三种情形下DG运营商的投资费用、卖电费用、运维费用依次增加,出现这种情况的原因是随着DG运营商在模型中角色的转变,会选择通过增设DG获取政府补贴以及卖电的方式获得更高的收益。此外,DG运营商的总收益在三种情形下依次增加,这说明考虑DG运营商自身的收益时,能获得比各自优化更大的收益,符合电力市场环境下各主体追求各自利益最大化的实际情况。

表9 9节点实际配网系统使用不同规划模型时的DG运营商费用Table 9 DG investment operator fees in the 9-bus actual distribution network system 万元

图9为三种情形下配电网投资运营商的年化成本变化情况。配电网运营商在线路规划方案已经确定的前提下会选择通过增加DR减少购电的方式减少其年化成本。情形2、3与情形1相比,DR管理费用略有增加,而表征配电网社会或者环境效益的网损成本以及碳排放惩罚费用等均降低,这说明当考虑源-网共同利益或者源-网主体博弈时,能够提升用户参与DR的积极性,积极响应电价变化。

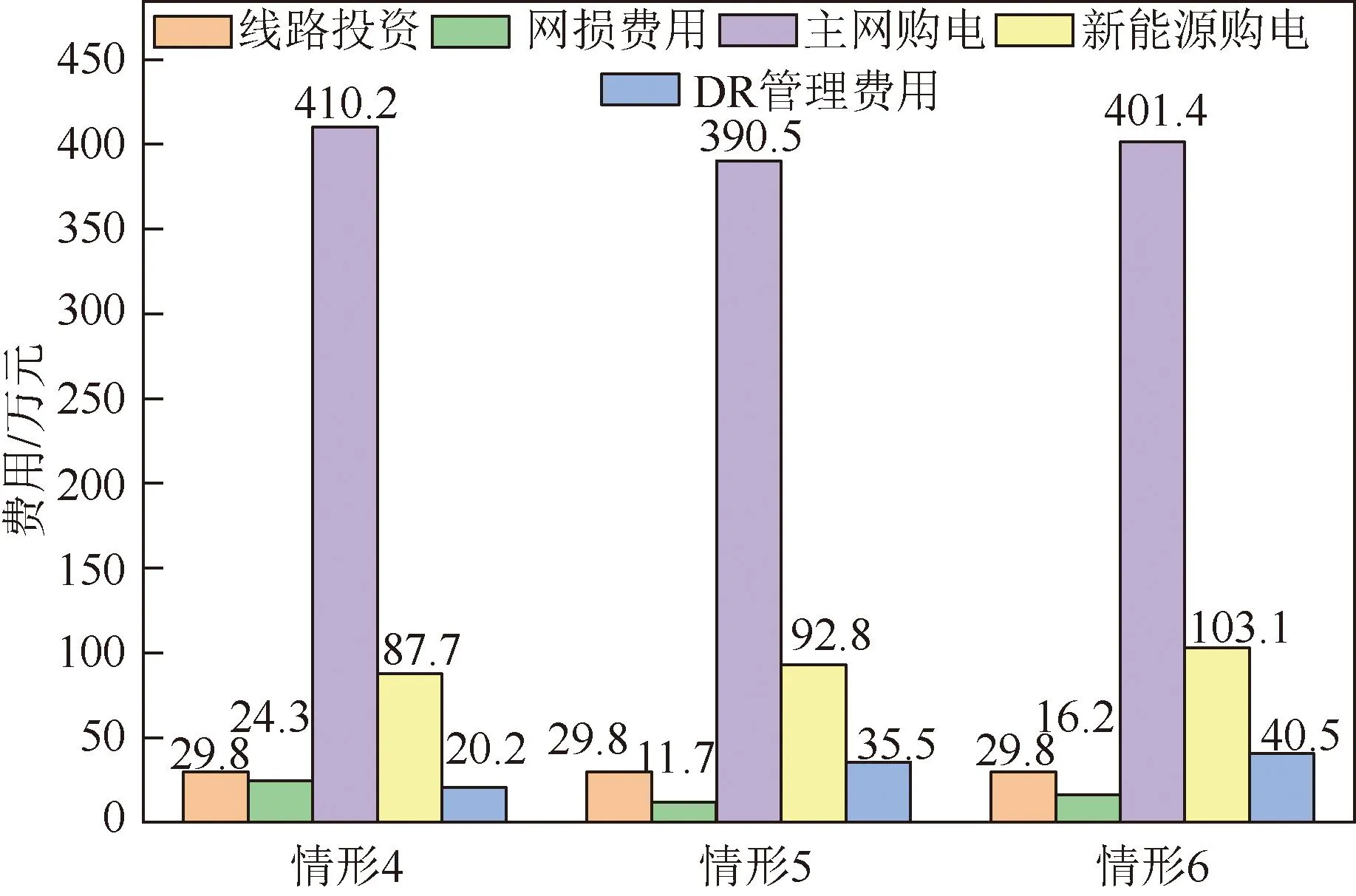
图9 不同规划模型的配电网运营商费用变化情况Fig.9 The fees changes of distribution network operators with different planning models

算例显示,当使用源-网-荷协调互动模型时,接入DG总容量为1 MW,最小年化成本为630.2万元。

2)电力市场因素对规划结果的影响分析。

按照6.1.2节第二部分所述,在实际算例验证不同电价机制对配电网规划的影响。规划结果如表10所示。

表10 9节点实际配网系统使用不同电价机制的规划结果Table 10 Planning results based on different electricity price mechanisms in the 9-bus actual distribution network system

由表10可知,情形5、情形6的规划结果完全相同。情形4与情形5、6相比,规划结果略有不同:新增DG数量减少1台。

图10为三种情形下配电网投资运营商的年化成本变化情况。由图10可知,情形4中主网购电费用较情形5、6高约25万元,这是因为峰谷电价均值较之日前电价高,从主网的购电费用会相应增大。

图10 不同电价机制下配电网运营商费用变化情况Fig.10 The fees changes of distribution network operators under different electricity price mechanism

7 结 论

本文针对电力市场环境下配电网中各主体互动响应关系复杂,追求自身利益最大化的问题,提出一种基于博弈论的源-网-荷协调互动规划模型,并采用基于改进粒子群算法的迭代搜索法求解,研究结果表明:

1)源-网-荷协调互动规划使配电网中各个主体均能综合各方信息,通过博弈不断优化自身决策,实现分布式电源、网架合理规划,提高用户侧电能使用效率,在电力市场环境下具有较强的适应性;

2)在源-网-荷协调互动规划中采用日前电价,较之峰谷电价能降低配电网运营商的购电费用,挖掘用户的需求侧响应潜力,达到延缓线路和分布式电源投资的目的;

3)在源-网-荷协调互动规划中采用节点边际电价时,由于边际递增效应的存在会导致配电网运营商购电成本增加,但仍小于未进入市场前的花费。

在本文所述方法中,主要考虑日前电价对规划结果的影响,在实际中还面临批发市场中现货与中长期比例的变化、用户侧多零售主体博弈等的挑战,在后续规划研究中,还需要建立更为精确的电力市场模型。

致 谢

本文得到了国网山西省电力公司科技项目(520533230001)的资助,在此表示感谢。

附录A

该配电示范区建设采取渐进过渡式的发展进程,分两期进行:

第一期建设:计划新建及改造线路3.5 km,其中2.5 km采用LGJ-150型架空绝缘导线,1 km采用LGJ-240型架空绝缘导线,新增线路如图8中虚线表示。同时,规划中计划完成整村屋顶光伏发电项目建设。根据屋顶面积及条件,总装机容量不超过5 MW。

第二期建设:聚合用户侧灵活性资源,参与需求侧响应服务,加强源荷互动,促进新能源消纳。

综上,该实际算例需要设计线路以及分布式光伏的规划方案,并在此基础上聚合9节点系统灵活资源,提升系统灵活性,可以进行仿真算例分析。

新增负荷节点为10、11、12、13,各负荷节点参数如表A1所示。

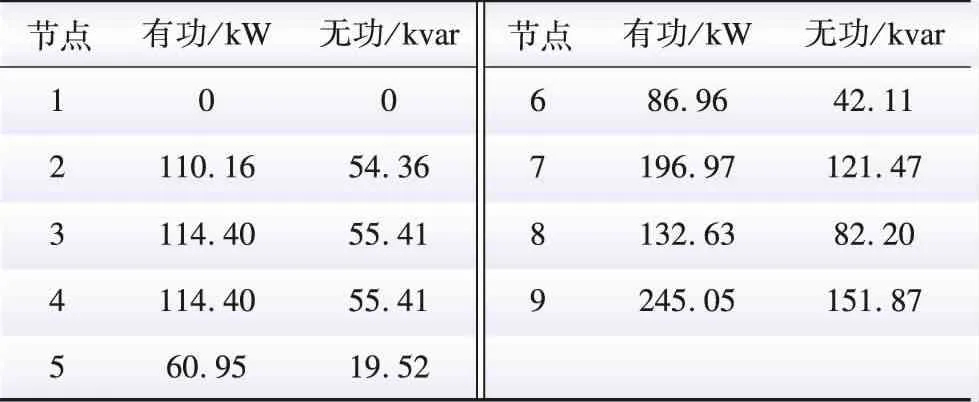
表A1 9节点配网系统负荷节点参数Table A1 9-bus distribution network system load node parameters

根据实际算例概况,新建线路已经确定,无需再次规划,运行以及待接入线路参数如表A2、A3所示。表中R为线路电阻,X为线路电抗。

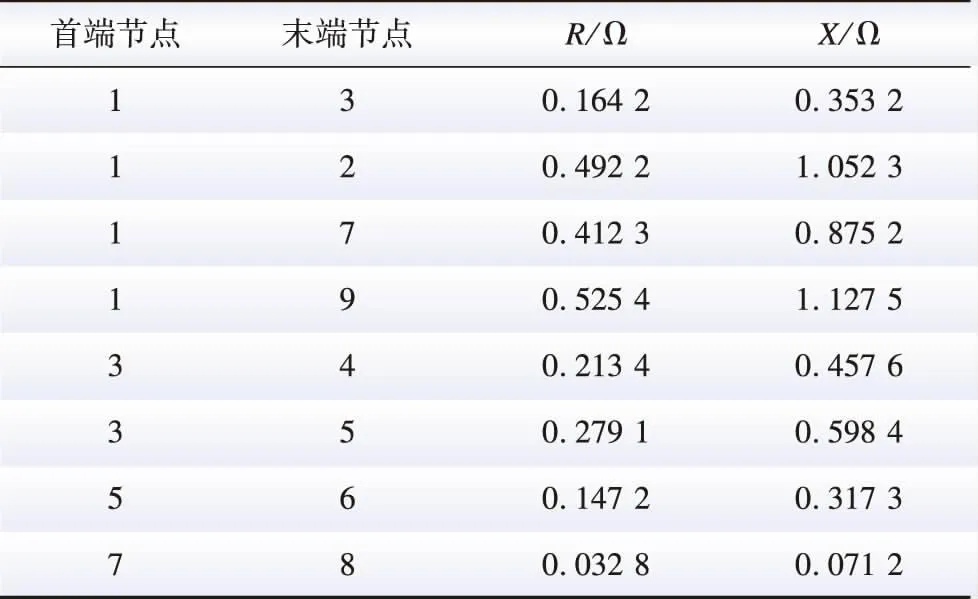
表A2 9节点系统运行参数Table A2 9-bus distribution network system operating parameters

分布式光伏待接入位置为节点2、3、4、5、6,其余参数均与测试算例相同。