交直流混联系统暂态功角稳定评估及特征量可解释性分析

李雅晗,夏世威,马琳琳,赵康,李新

(1. 华北电力大学电气与电子工程学院,北京市 102206;2. 国网山东省电力公司电力调度控制中心,济南市 250000;3.国网山东省电力公司电力科学研究院,济南市 250000)

0 引 言

新能源和直流并网使传统电网的拓扑结构更加复杂,其动态特性亦对交直流混联系统的暂态功角稳定产生较大影响[1]。如何高效准确评估含新能源的交直流混联系统的暂态功角稳定性(transient angle stability assessment, TASA)并进行关键影响因素的解释性分析具有重要意义。

目前,国内外采用人工智能的方法研究暂态功角稳定评估问题成为热点,如支持向量机(support vector machine, SVM)、决策树(decision tree, DT)及其改进算法等浅层学习方法[2-6],也有通过深度学习[7-11]如卷积神经网络(convolutional neural networks,CNN)、深度神经网络(deep neural networks,DNN)等方法进行复杂的暂态功角稳定评估分类。文献[12]提出了基于SVM集成模型的交直流混联系统暂态稳定评估方法,通过机理分析表明新能源和直流特征量能够表征交直流混联系统的暂态稳定性。文献[13]根据多类间线性判别分析法,基于系统的轨迹簇特征对含新能源的交直流混联系统进行暂态稳定分析。上述方法有效评估了交直流混联系统的暂态稳定性,并说明了新能源和直流特征量与系统暂态稳定性间的相关性。文献[14]基于极致梯度提升树(extreme gradient Boosting, XGBoost)算法对电力系统进行暂态稳定评估,说明了模型的可靠性和有效性。但以上评估模型均为“黑箱”结构[15],无法阐明新能源、直流等特征量是如何影响系统的暂态稳定性,因此亟需研究可解释性方法以实现特征量和暂态稳定结果间的关联关系阐释。目前有少量文献进行了可解释性研究,文献[16]构建DT模型对暂态稳定评估分类结果进行解释,但其采用的单一可解释性模型迁移性较差,且无法对大量数据进行快速评估。文献[17]利用局部可解释性方法对暂态功角稳定评估结果进行单个样本的解释,但其无法对特征量进行全局解释性分析,难以呈现特征量值的大小与暂态功角稳定的整体相关性。

为了有效评估交直流混联系统中暂态功角稳定特性并准确分析新能源、直流特征量对系统稳定性的影响,本文首先基于XGBoost算法构建暂态功角稳定评估模型,选择电力系统中新能源和直流特征量作为暂态功角稳定评估模型的输入,并根据sigmoid函数得到样本预测值与稳定性间的关系,之后基于SHAP(Shapley additive explanations)提出特征量的可解释性分析方法,最后对所提的暂态稳定评估模型进行仿真验证,并从两方面对特征量进行解释:1)从全局出发对特征量进行重要性排序,挖掘对系统暂态功角稳定影响最大的新能源和直流特征量,并分析特征量的Shapley值与样本预测值间的关系,进一步说明特征量的Shapley值的正负对暂态稳定结果呈现抑制和促进2种特性,从全部样本的角度得到特征量值大小与暂态功角稳定之间的关联关系。2)从局部对单个稳定与失稳样本进行解释,说明特征量对样本预测值的影响关系,从而提高稳定评估结果的可信度。

1 XGBoost算法

为了得到暂态功角稳定结果与特征量间的映射关系,可以将暂态功角稳定评估问题转化为二分类问题[18],因此本文引入一种分类器XGBoost模型用于暂态功角稳定评估,并采用并行计算模式进行学习,并结合多个弱学习器提高模型的训练效率和准确率。该模型具体如下[19]:

设样本集合D表示为:

D={(xi,yi)|i=1,…,N,xi∈RM,yi∈R}

(1)

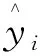
(2)

式中:fk(xi)为第k棵树对第i个样本的计算分数。XGBoost包含参数优化及目标函数优化,其中参数优化通常采用网格搜索和交叉验证方法得到模型最优参数,目标函数优化可以提高分类的准确率,并以最小化损失函数和增加模型复杂度为目标,如式(3)所示:

(3)

(4)

(5)

式中:T为树的叶子节点数;ωj为叶子节点j的权重;γ为惩罚系数,用于控制模型叶子节点个数;λ为正则项系数,用于调节节点的权重分布,一般情况下取值为1。由于XGBoost以树模型迭代相加的方式进行训练,每增加一个决策树函数fk可使目标函数进一步减小,ft表示fk迭代第t次时的最优树结构,使用二阶泰勒公式展开并去掉常数项后,可将目标函数改写为:

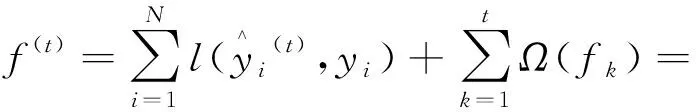
(6)

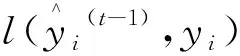
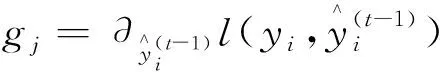
(7)

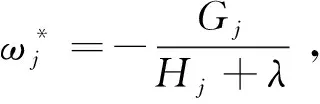
(8)

(9)

基于p∈(0,1),可以将样本i进一步标签为0或1,设定标签0代表稳定样本,1代表失稳样本,得到标签与概率值p1、p2之间的关系:

(10)

2 基于SHAP的特征量可解释分析

(11)

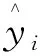
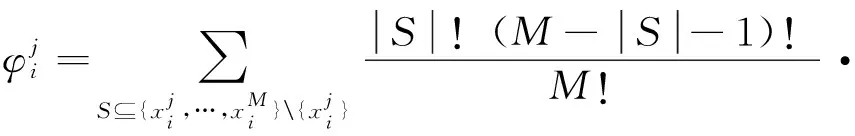
(12)

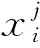
SHAP对特征量的局部可解释性表现为:对样本i而言,可依据式(11)将各特征量Shapley值之和加上样本预测的基准值等于模型的输出结果,从而可通过这一线性关系反映各特征量对某一稳定或失稳样本结果的渐进影响过程。特征量的可解释性示意如图1所示。

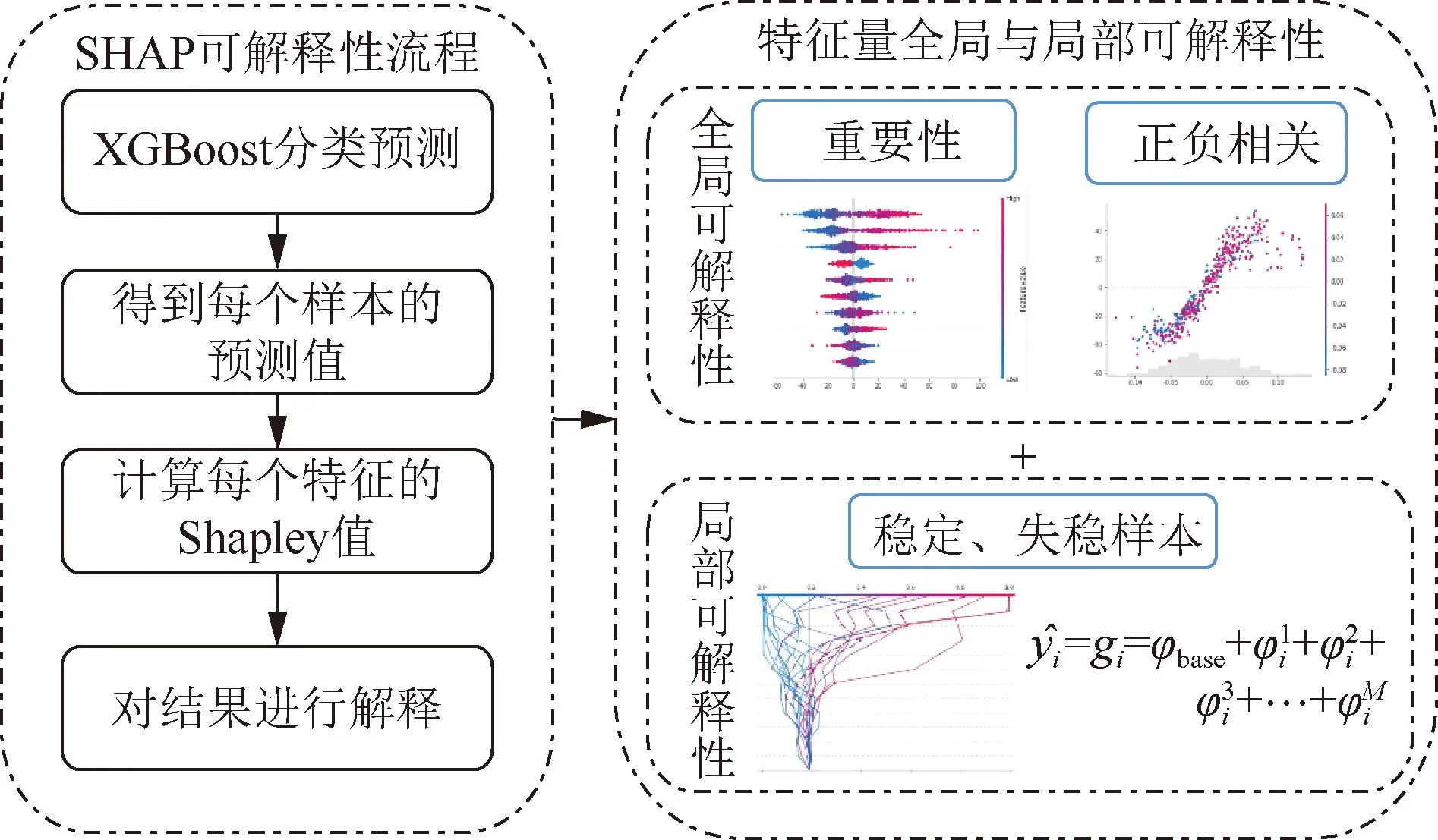
图1 特征量的可解释性示意Fig.1 Interpretability of features

3 交直流混联系统暂态功角稳定评估模型

3.1 交直流混联系统特征量

暂态功角稳定评估首先需要一组特征量,再通过XGBoost分类器建立特征量与系统暂态功角稳定性间的映射关系[22]。特征量需要能表征系统的暂态功角稳定性、具有明确的物理意义;同时大量的特征量会增加模型训练时间且影响模型训练效率,因此特征量不宜过多。本文研究含新能源的交直流混联系统的暂态功角稳定性,因此主要选择新能源和直流特征量;同时由于发电机相对功角Δδ直接影响了系统的功角稳定[23],将其作为特征量以对比分析新能源和直流特征量对功角稳定性的影响;且光伏电站通常为直流发电,并通过逆变器将其转换为交流电供电网络使用,因此光伏电站的输出功率主要是有功功率,而无功功率相对较小,因而可以忽略。综上参考文献[6,12]得到如表1所示的特征量集合,包括各发电机相对功角Δδ;HVDC直流输电线路两端节点电压UHVDC、HVDC直流输电线路电流IHVDC、HVDC直流输电线路两端功率PHVDC、HVDC直流输电线路触发延迟角α、HVDC直流输电线路熄弧角γ;各风电机组并网节点电压UWP、输出有功功率PWP、输出无功功率QWP;各光伏电站并网节点电压UPV、输出有功功率PPV。

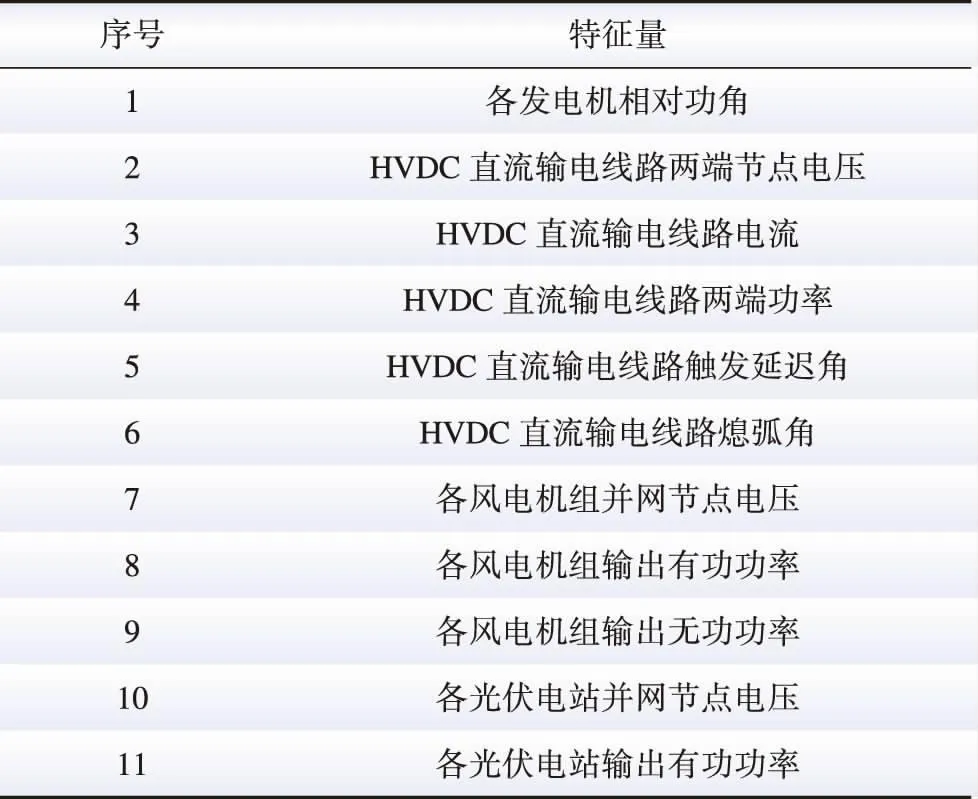
表1 暂态功角稳定评估的特征量Table 1 Features of TASA

3.2 稳定评估模型的评价指标

通过暂态稳定指标(transient stability index, TSI)可以表征系统的暂态功角稳定性[24-25],TSI计算公式为:

(13)

式中:Δδmax为扰动后任意两台发电机的最大相对功角差。暂态功角稳定评估作为一个二分类问题,可基于式(13)的TSI进行标签以判断系统稳定性,即当TSI>0时,系统暂态功角稳定,样本标签为0;当TSI<0时,系统暂态失稳,样本标签为1。进一步定义如表2所示的指标对模型分类效果进行评价[26],其中TP为预测正确的稳定样本数量;TN为预测正确的失稳样本数量;FN为预测错误的稳定样本数量;FP为预测错误的失稳样本数量。

准确率ηAccuracy指预测正确的样本数占总样本数的比例,越接近1表明模型整体效果好。

(14)

召回率ηRecall是少数类样本中预测正确的样本所占比例。由于暂态功角稳定样本集中失稳样本数量相对稳定样本较少,且将失稳样本误判为稳定样本的代价更大,因此可通过召回率指标式(15)反映失稳样本误判情况,召回率越高失稳误判越少。

(15)

3.3 稳定评估模型的分析流程

为解决交直流混联系统暂态功角稳定评估及特征量的可解释性问题,将模型评估分为3个部分,分别是离线训练、在线评估及结果的可解释性分析,其流程如图2所示。

图2 暂态功角稳定评估流程Fig.2 Flow chart of TASA

1)离线训练阶段:首先通过时域仿真得到如表1所述的不同运行方式下暂态功角特征量集合。将特征量集合及对应的标签分别作为评估模型的输入和输出并随机划分为训练集和测试集,通过训练集对XGBoost模型进行训练,并根据网格搜索和交叉验证计算模型最优参数,最后通过测试集和模型分类性能指标对模型进行评价。

2)在线评估阶段:通过实时量测系统获得数据集并得到特征量集合,将特征量数据输入已训练好的XGBoost模型中,分类预测系统的暂态功角稳定或失稳状态。

3)解释性分析阶段:基于SHAP对XGBoost模型特征量和分类预测结果进行全局和局部解释,分析交直流混联系统特征量对暂态功角稳定的影响关系。

4 算例分析

本节基于某实际交直流混联系统对所提暂态功角稳定评估模型的有效性进行验证。算例拓扑如图3所示,该系统共包含53个节点,风火打捆经3回交流线路和1回±500 kV HVDC直流输电线路送出系统,装机占比为:新能源(480万kW)/常规(600万kW)=1/1.25。其中光伏电站4台,风电机组8台,常规火电机组10台(以Gen4A-1作为参考机组)。

图3 算例拓扑Fig.3 Example topology

采用电力系统仿真软件PSD-BPA对系统进行机电暂态仿真,构建新能源(风电汇集站A、B,光伏汇集站C)同时率(新能源占所有出力的比例)分别为0、20%、50%、60%四种场景,对26条线路进行三相永久N-1故障,设置故障位置距离线路首段25%、50%、75%,故障发生时间为第50周波(1 s),故障清除时间为故障发生后的第7周波(0.14 s)到第15周波(0.30 s)共9种。根据TSI对仿真产生的2 764个样本进行暂态功角稳定判断,其中稳定样本1 834个,失稳样本930个,并随机选取训练集和测试集且设置比例为7∶3。

4.1 分类器算法对比

针对暂态功角稳定评估中的分类器模型,采用python 3.9.12在Scikit-learn平台进行搭建。为验证XGBoost模型的有效性将XGBoost与其他主流分类模型进行对比[27-30],包括AdaBoost、随机森林(random forest, RF)、K近邻法(K-nearest neighbor, KNN)、SVM。其中XGBoost、AdaBoost、RF均为树模型,采用100棵树,其余算法采用默认参数。通过准确率、召回率和模型训练时间t来评价分类器性能,对比结果如表3所示。

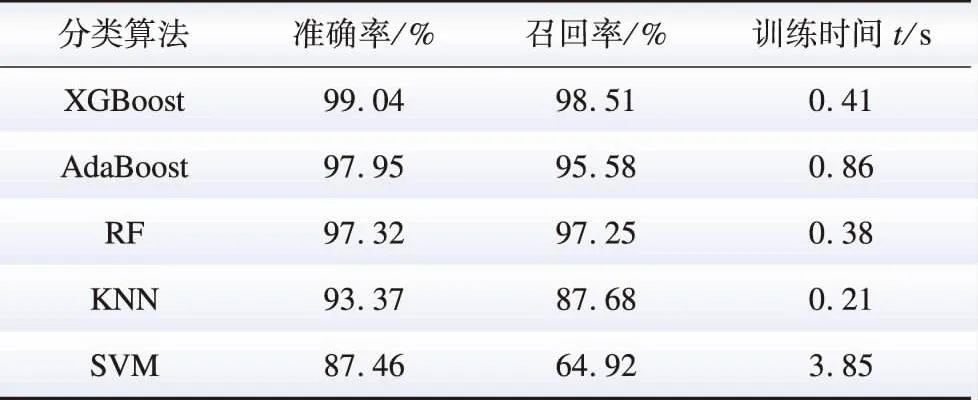
表3 分类算法性能对比Table 3 Performance comparison of classification method

结果显示,本文的XGBoost相较于其他算法,准确率和召回率都较高,且训练时间也较短,能够准确地对输入样本进行预测分类。XGBoost、AdaBoost和RF都属于树结构模型,AdaBoost的准确率、召回率低于XGBoost,且训练时间较长;RF与KNN虽然都能快速对模型进行训练,但是召回率和准确率均低于XGBoost;SVM结构简单,处理大量数据误差较大,整体性能较差。

4.2 交直流混联系统特征量的可解释性

4.2.1 特征量的全局解释

将所有样本的特征量进行Shapley值的计算,该Shapley值可以反映特征量对暂态功角稳定的重要性并对特征量进行全局解释。由表1得到61维特征量,通过式(12) 得到各特征量对应的Shapley值,并根据绝对值大小进行重要性排序,选择前20维特征量如图4所示,主要包括HVDC直流输电线路触发延迟角α、熄弧角γ、各发电机相对功角Δδ及各风电机组、光伏电站并网节点电压U、输出功率P等。图中横坐标为特征量的Shapley值,同时每个样本点的颜色反映特征量值本身的大小。

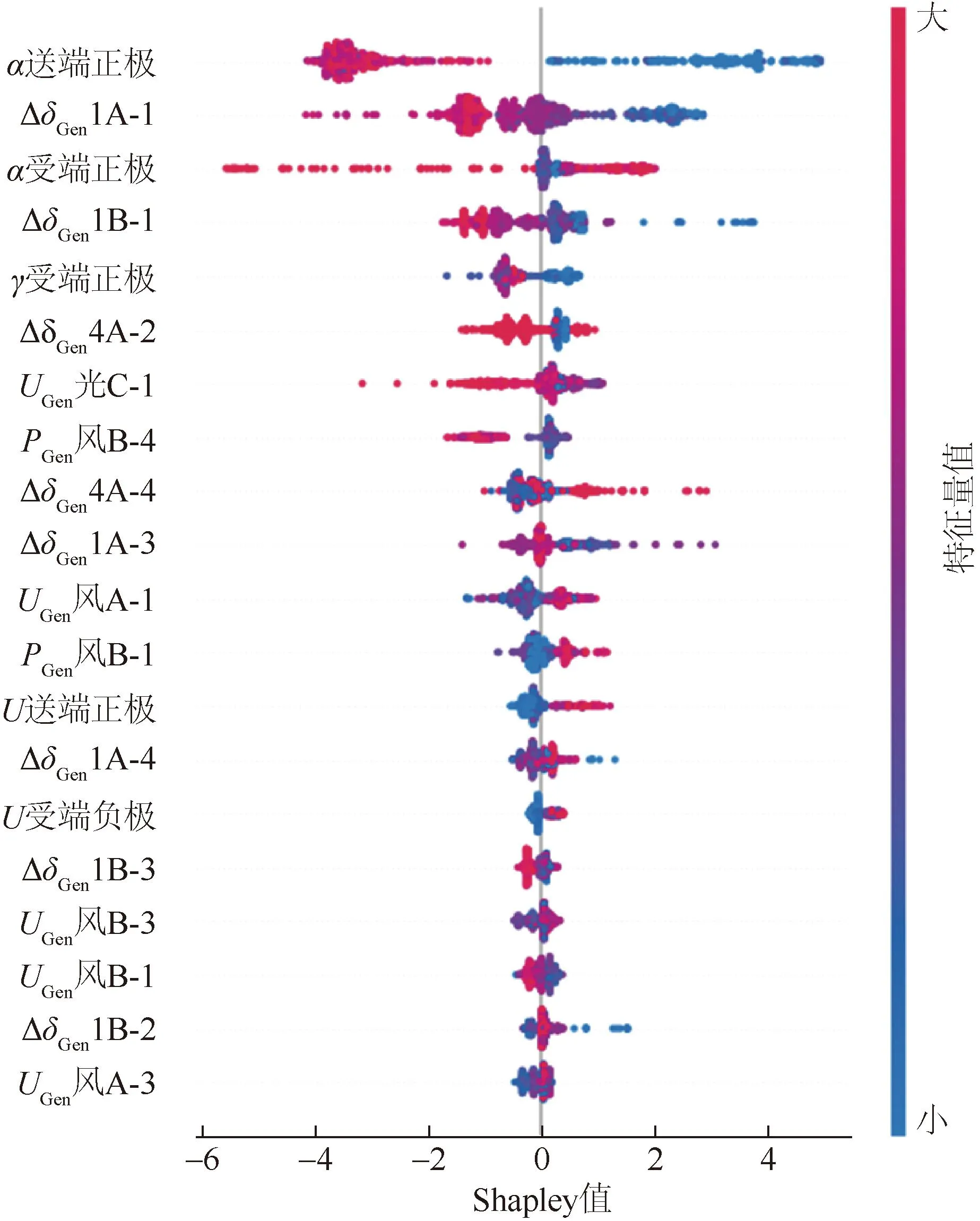
图4 特征的重要性排序Fig.4 Importance ranking of features

以HVDC直流输电线路送端正极触发延迟角“α送端正极”和光伏电站C-1的并网节点电压“UGen光C-1”为例,其对应的特征量Shapley值如图5所示。以特征量值为横轴,特征量的Shapley值为纵轴以反映特征量与稳定性的关联关系。由式(9)-(11)可知,当特征量的Shapley值大于0时,此时特征量对预测值有正向影响作用,即对系统失稳有促进作用;当Shapley值小于0时,特征量对失稳结果有抑制作用。

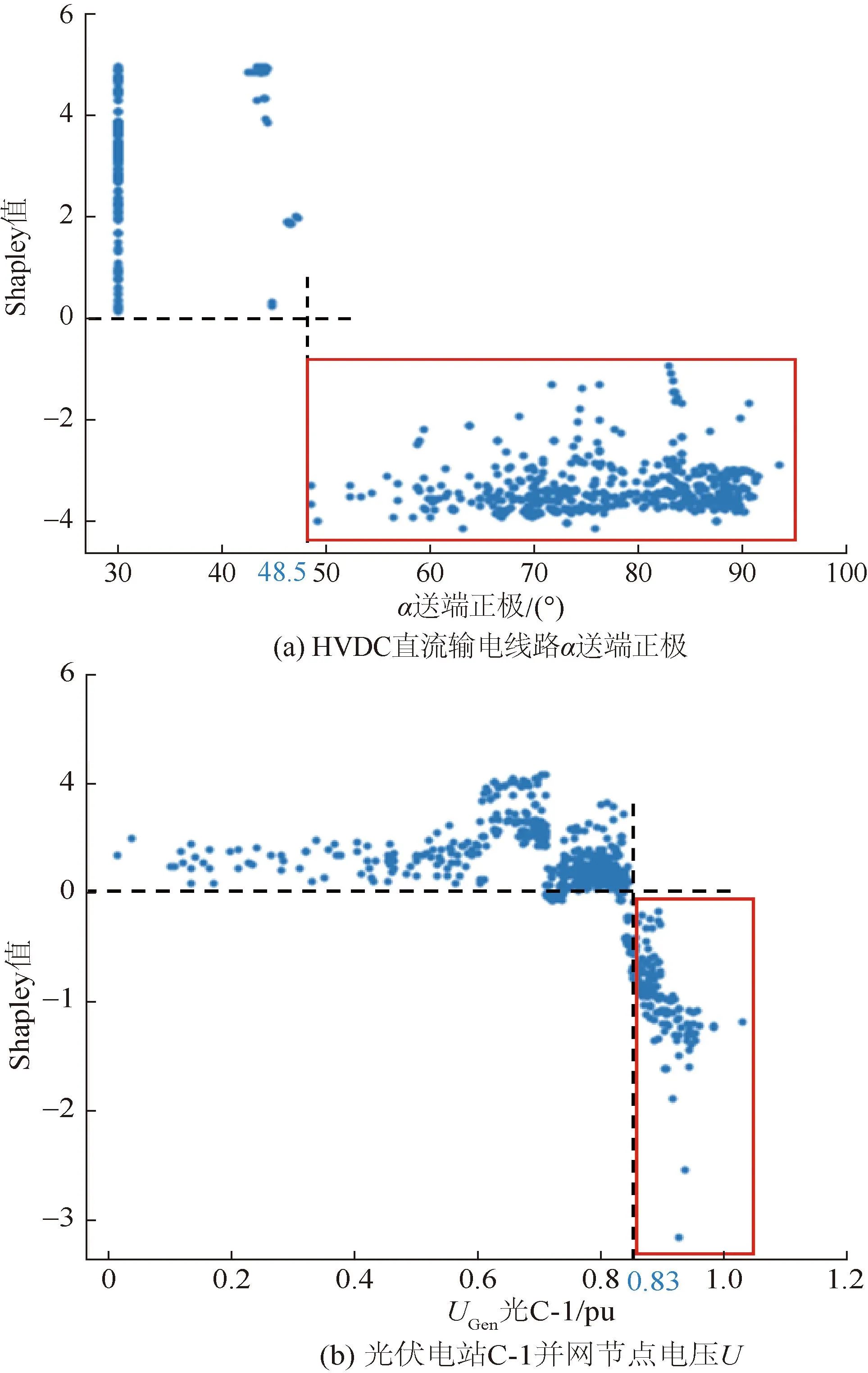
图5 特征量Shapley值Fig.5 Shapley value of features

如图5(a)所示当直流送端正极触发延迟角α=30°时,Shapley值恒大于0,此时α促进系统失稳,当α≥48.5°时,Shapley值恒小于0,抑制系统失稳;如图5(b)所示,当光伏电站并网节点电压U小于0.83 pu时,Shapley值大于0,促进系统失稳,当U大于0.83 pu时,Shapley值小于0,抑制系统失稳。通过同样方式,可对其他系统特征量展开分析,解释各特征量对系统暂态稳定性的影响。

4.2.2 特征量的局部解释

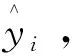
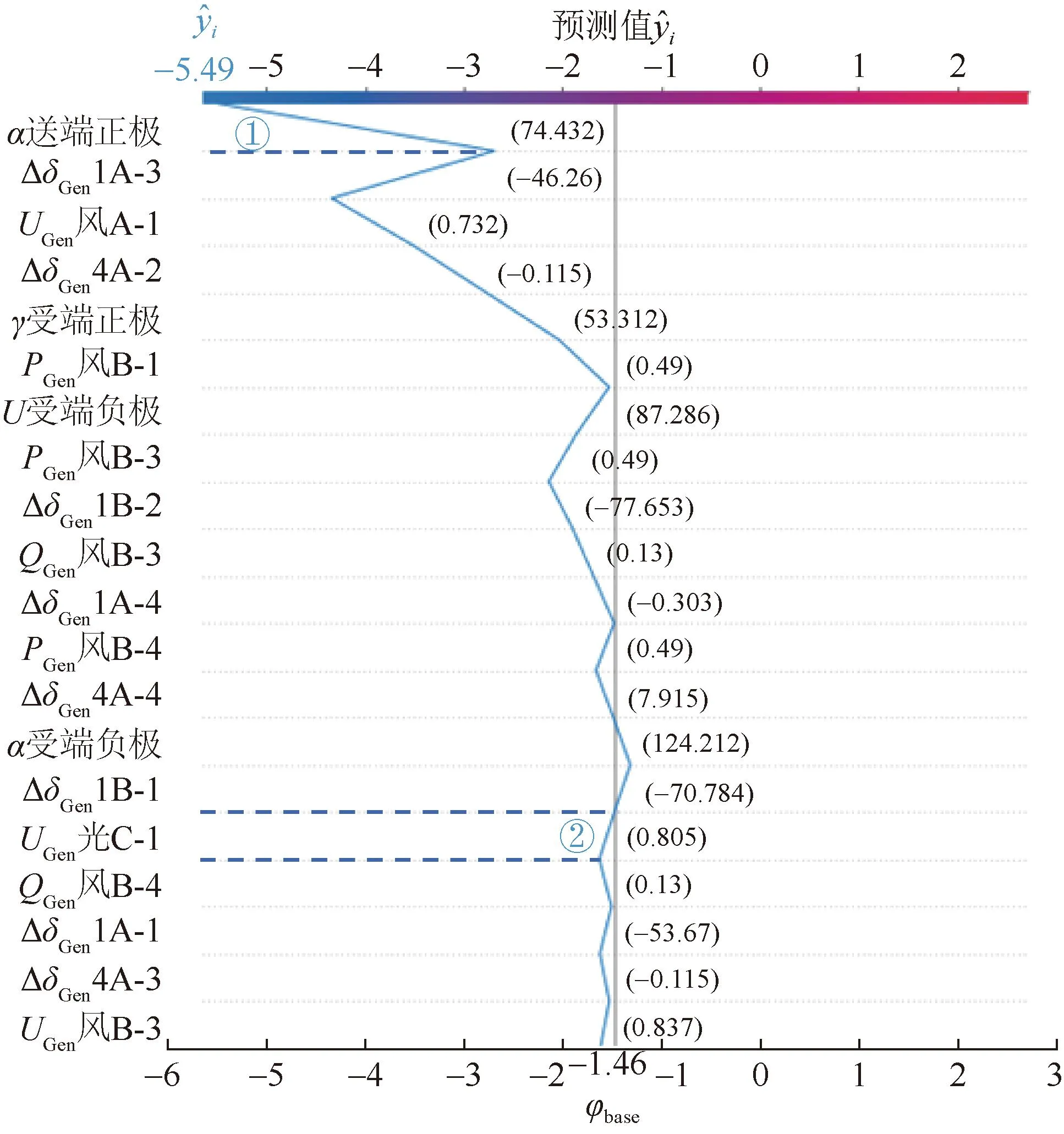
图6 单个稳定样本预测结果Fig.6 Prediction result of single stable sample

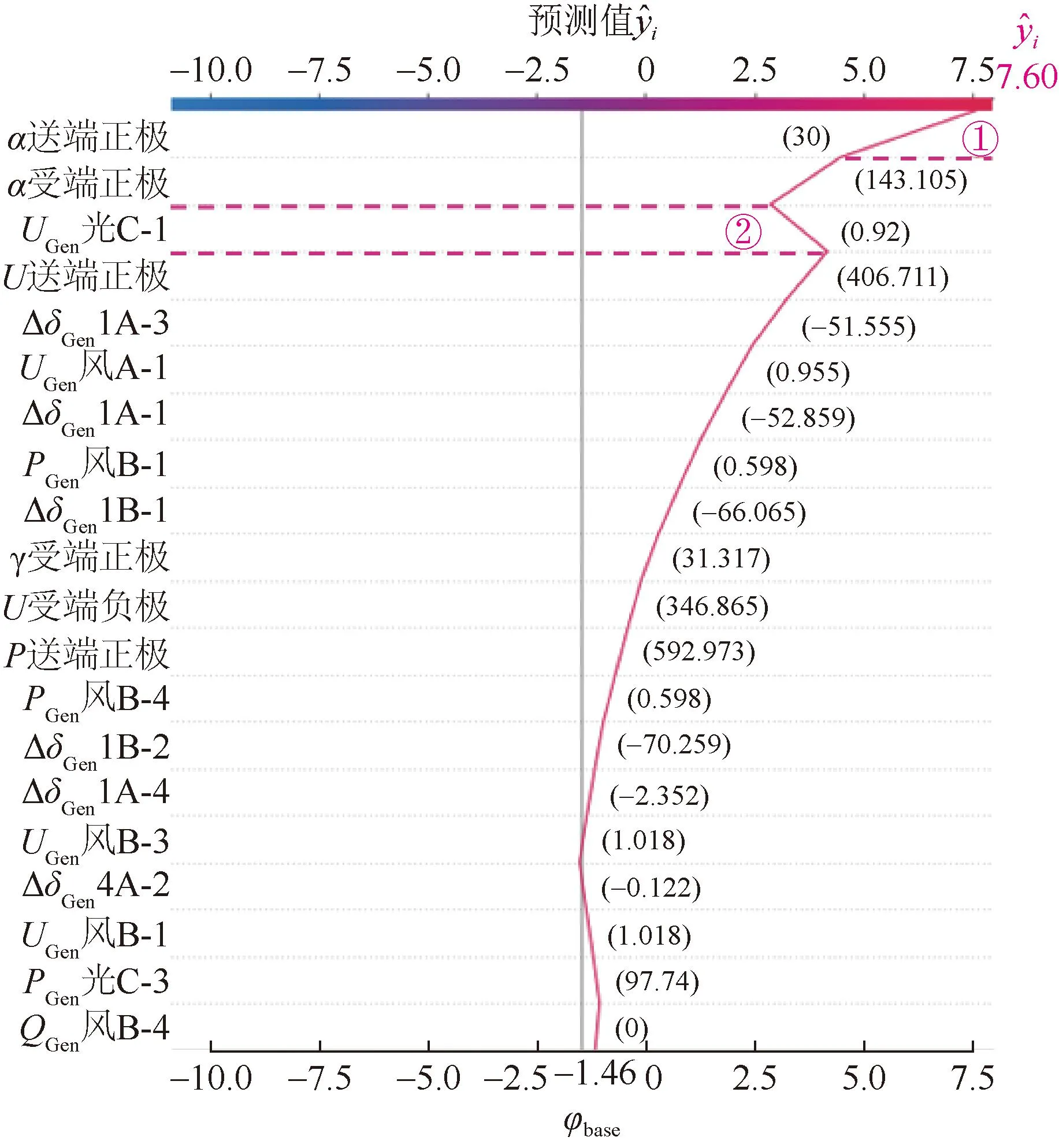
图7 单个失稳样本预测结果Fig.7 Prediction result of single unstable sample

5 结 论

为研究交直流混联系统暂态功角稳定性并解释影响因素,本文提出了一种基于XGBoost算法的交直流混联系统暂态功角稳定评估方法,通过sigmoid函数得到样本预测值与暂态功角稳定性间的关系,并提出基于SHAP的特征量可解释分析方法,根据预测值与各特征量的Shapley值的线性关系解释了特征量的Shapley值与系统功角稳定性间的影响关系,最后通过含有新能源和直流接入的某500 kV实际算例系统验证了所提功角稳定评估模型的有效性。仿真结果表明:

1)基于XGBoost算法的暂态功角稳定评估方法,并选择新能源和直流特征量作为稳定评估模型的输入能够对交直流混联系统的稳定或失稳进行有效预测。

2)提出的基于SHAP的特征量可解释分析方法能对全部样本和单个样本进行全局和局部解释性分析,从而反映交直流混联系统中新能源和直流特征量对暂态功角稳定的影响关系。

3)暂态功角稳定评估方法及特征量可解释性分析方法结合,为交直流混联系统功角稳定性评估及影响因素分析提供了准确、可解释的分析工具,可为新型电力系统的安全运行提供决策依据。