考虑阶梯型碳交易的多负荷聚合商协同优化调度与成本分配

任洪波,王楠,吴琼,时珊珊,方陈,万莎

(1. 上海电力大学能源与机械工程学院,上海市 200082;2. 国网上海市电力公司电力科学研究院,上海市 200437)

0 引 言

随着碳达峰、碳中和目标的快速推进,可再生能源愈发受到关注[1]。然而,可再生能源具有间歇性和波动性等特点,导致电力供给侧与负荷侧叠加波动,系统稳定性面临巨大挑战[2]。需求响应可充分利用负荷侧灵活性资源,主动适应供给侧出力,从而为电力系统的灵活调度打开新的局面[3]。然而,单个需求侧资源由于体量限制,存在弹性水平较低、可调容量较小等问题,很难独立参与需求响应。负荷聚合商(load aggregator,LA)应运而生,可针对不同类型用户,评估其可调节潜力,并整合分散响应资源参与电力系统的灵活性调度[4]。

目前,国内外有关LA的研究主要集中在优化运营和市场竞争策略[5-6]。文献[7]通过LA聚合需求侧电动汽车可调控资源与电网进行互动,提出了考虑响应可靠性的时空双层调度模型,为电网提供辅助服务。文献[8]通过LA聚集用户侧空调和电动汽车等灵活性资源,提出了考虑分布式电源运营商在内的多主体优化运行模型。文献[9]通过LA聚集居民用户侧柔性负荷资源,提出考虑负荷类型细分和非合作博弈的LA日前投标模型。文献[10]通过LA聚合需求响应负荷,提出了考虑用户偏好和LA收益的主从博弈模型。然而,上述研究只考虑了单个LA为主体参与电力市场的响应策略和运行调度。虽然文献[11]通过LA聚合不同类型用户的柔性负荷,提出了考虑用户用电特性差异的合作联盟运营模型,但如何利用不同类型用户的负荷特性差异深度参与需求响应尚待研究;同时,各LA之间由于合作而产生的成本分摊问题亟待解决,联盟稳定性难以保证。

另一方面,文献[12]针对工业用户提出了考虑阶梯型碳交易机制和不同购电来源的综合需求响应策略。文献[13]将碳交易与综合能源系统规划相结合,以碳交易和系统投资运行成本最小为目标,构建低碳经济能源站规划模型。文献[14]将电动汽车作为灵活性调控资源,建立了考虑碳交易机制和电动汽车充电负荷调节比例的综合能源系统调度模型。文献[15]为实现园区低碳经济运行,建立了基于价格型需求响应策略和阶梯型碳交易机制的综合能源系统日前低碳优化调度模型。文献[16]探讨了考虑氢能和阶梯式碳交易机制的综合能源系统柔性运行机制。然而,上述研究未考虑同时赋予负荷聚合商碳交易集成商的角色,使得碳交易市场和电力市场相互决裂,无法实现优势互补并达到两者间协同优化的目的。

为充分挖掘基于不同类型用户负荷互补特性的需求响应潜力,本文结合碳交易市场,提出一种考虑奖惩阶梯型碳交易和成本分配的多负荷聚合商优化调度模型。首先,引入多类型负荷聚合商分别代表不同类型用户(工业类、商业类和居民用户类等),并根据各类用户的柔性负荷将其细分为可削减、可转移、可平移3种类型,构建参与调度的需求响应模型;然后,采用预测电负荷法为系统无偿分配碳排放配额,并考虑热电联产设备以及外购电力的实际碳排放量,构建奖惩阶梯型碳交易模型;在此基础上,引入合作博弈理论,确立多LA合作运营架构,并以联盟整体日运营成本最低为目标,构建多个LA间交互合作的日前运行优化模型并进行求解。为了确保通过合作形成的整体运营成本降低效果在所有参与者间的公平、合理共享,采用合作博弈的经典解Shapley值法,按照每个参与者对联盟所作贡献的大小对整体运营成本进行分配,确定最终各LA运营成本,实现整体利益与个体利益共赢。

1 负荷聚合商合作运营架构

LA作为需求侧资源的聚合者,可通过与用户签订协议来获得其详细用能信息的代理权,并通过专业技术手段评估不同用户的需求响应潜力。本文着重讨论LA与日前电力市场的投标策略及其成本分配原则,建立了多个LA代理多类型用户的日前投标合作联盟运营模型。LA合作联盟运营架构如图1所示,所代理的用户类型主要包括居民用户、商业用户和工业用户等。由于各类型用户之间存在用能特性差异,各代理商LA可基于合作联盟,进行相互间能源共享和交易,从而减少外购电力,降低整体用能成本,实现联盟体的利益最大化。

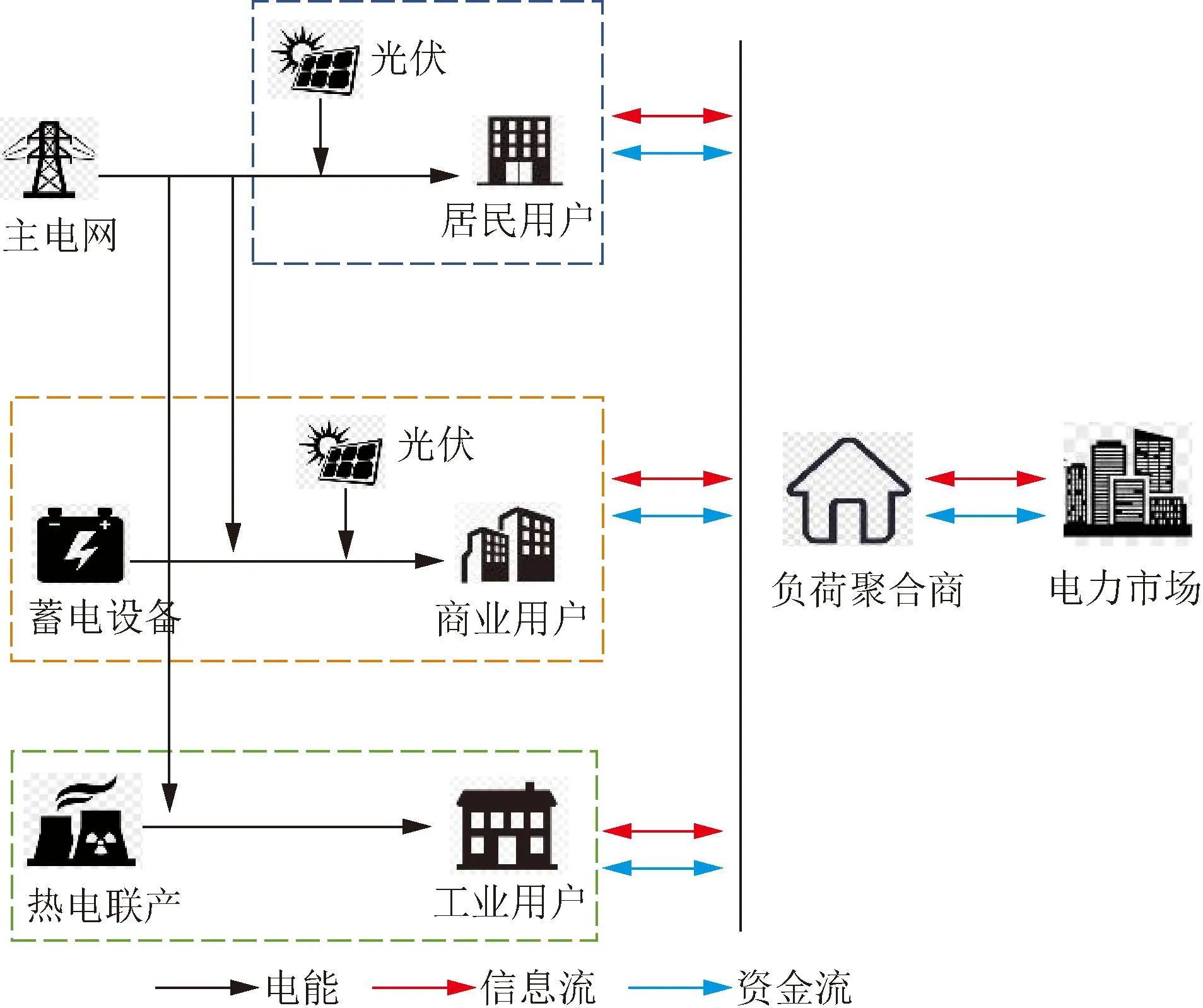
图1 LA运营架构Fig.1 Operating structure of LA

具体流程如下:

1)电力调度部门根据其内部负荷预测模型,并将次日的电价与时段信息传递给LA;

2)各类用户将其柔性负荷信息上报给LA;

3)在信息透明且安全的环境下,基于合作博弈运营模式,以整体运营成本最低为目标,确定参与需求响应资源的投标量以及各LA之间的合作策略,对用户的柔性负荷资源进行优化调度。

2 柔性负荷分类和建模

2.1 可调度柔性负荷分类

可调度柔性负荷用户可以通过与LA签订负荷削减、转移和平移合同来参与需求响应。为使合同设计更加合理化、定制化,LA需要对其管理的柔性负荷用电特性和用电趋势进行分析和预判,以确定不同类型用户参与响应的积极性和互补特性。参与LA优化调度的负荷主要分为高负荷率型负荷、迎峰型负荷和避峰型负荷[15]。居民用户负荷大多属于避峰型负荷,每小时最大可削减量约为最大负荷值的30%;商业用户负荷大多属于迎峰型负荷,且削减能力有限;工业用户负荷大多属于高负荷率型负荷,与行业特性、季节特点等因素联系密切。

2.2 可调度柔性负荷建模

1)可削减负荷模型。

可削减负荷指运行时间段不改变,运行功率可削减的柔性负荷。该类负荷主要包括电灯、空调等工作模式不固定的电器设备,对该类负荷用式(1)和式(2)统一建模。可削减负荷在满足用户基本用电需求和用电满意度的情况下进行部分削减,削减比例不应超过一定的限额,可约束为:

(1)

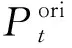
LA对可削减负荷的控制成本[12]可表示为:

(2)

式中:Ccurt为可削减负荷补偿成本;α1、α2分别为可削减负荷二次项、一次项常量系数。

2)可平移负荷模型。

可平移类负荷的用电特点是每天具有固定工作时长、固定功率及习惯使用时间,且一旦启动不宜中断。该类负荷主要包括洗衣机、烘干机等有固定工作模式的电器设备,对该类负荷统一建模为:

(3)

负荷平移前后保持所需电能不变,可约束为:

(4)

负荷平移前后为避免用户电费增加,可约束为:

(5)

当负荷平移到以τ为起始时间的区间内时,为满足运行时间连续,可约束为:

(6)

ft=0,∀t∉[tsh-,tsh+]

(7)

(8)

式中:τ为可接受平移时间段内的任意时刻;ft为t时刻可平移类负荷启动状态的0-1变量,ft=1和ft=0分别表示启动和不启动;ts为可平移类负荷持续时间。

式(6)表示可平移负荷的不可中断性约束,式(8)表示可接受的时间段内满足可平移负荷要求约束。

LA对可平移负荷的补偿成本,可表示为:

(9)

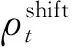
3)可转移负荷模型。

可转移类负荷的用电特点是没有固定的工作时间和工作时段,只需在规定时间区间内满足负荷需求即可,没有连续性约束。该类负荷的灵活性较高,主要包括空调、电动汽车等设备,对该类负荷统一建模为:

(10)

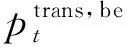
负荷转移前后所需电能保持不变,可约束为:

(11)

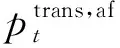
负荷转移前后为避免用户电费增加,可约束为:

(12)

LA对可转移负荷的补偿成本,可表示为:

(13)

3 奖惩阶梯型碳交易模型

本文在考虑园区参与碳交易市场的前提下,引入阶梯型碳交易机制。园区各设备运行过程中产生的CO2及外购电力核算之后的CO2会在碳交易市场进行交易。碳交易模型主要包括碳排放权配额、实际碳排放量及阶梯型碳排放交易3个环节,分别对这3个环节建立数学模型[19-21]。

3.1 碳排放权配额

碳排放权配额的分配方式有无偿和有偿2种方式,我国一般采用无偿配额的方式进行初始配额分配,然后各控排单位根据自身配额合理安排生产计划。当实际碳排放超过分配额度时,需要从碳交易市场或者其他排放源购买缺少的额度,否则需缴纳高额罚金;反之,当实际碳排放小于分配额度时,可将多余碳排放权配额出售。本文初始配额与预测电负荷相关联,如式(14)所示。

(14)

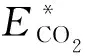
3.2 实际碳排放模型

1)热电联产设备CO2排放量。

热电联产设备以天然气为一次能源,其燃烧排放的CO2为:

(15)

(16)

式中:ECO2,g为天然气CO2排放量;FC,g、FCO2,g分别为天然气基于最低热值的碳排放因子和CO2排放因子(用于量化单位污染物排放量系数);Pchp,t为t时刻热电联产装置输出电功率[13];ηchp为热电联产机组的发电效率,其值为发电量与燃料输入量的比值。

2)外购电CO2排放量。

从电网购电时,需要计算外购电力的CO2排放量ECO2,e,计算公式为:

(17)

式中:PLA,i,t为第i个LA在t时刻从电网购买的电力;FCO2,e为电网基准线排放因子[17]。

本文所提及的园区综合能源系统的碳排放源主要有热电联产机组及上级电网购电,因此该能源系统的实际CO2排放量ECO2为:

ECO2=ECO2,g+ECO2,e

(18)

3.3 阶梯型碳交易成本模型

为进一步控制碳排放总量,激发各带有分布式电源的LA节能减排积极性,本文提出了基于奖励系数λ的奖惩阶梯型碳交易成本计算模型。规定若干排放区间,当实际碳排放量小于免费分配的碳排放额时,碳交易成本CCO2为负,表示供能企业可以出售多余的碳排放配额,并基于上述模型可以获得一定的技术补贴,碳排放量越小的区间对应的碳交易价格越高;反之,当实际碳排放量大于免费分配的碳排放额时,CCO2为正,表示企业需要购买碳排放权,碳排放量越大的区间对应的碳交易价格越高。应用此模型时,需将实际碳排放量进行分段线性化处理,碳交易价格与碳交易量关系如图2所示。从图2可以直观看出,正区间表示供能企业碳排放权不足,需要从碳交易市场购买;负区间表示供能企业有剩余碳排放权,可以出售获得收益[19]。

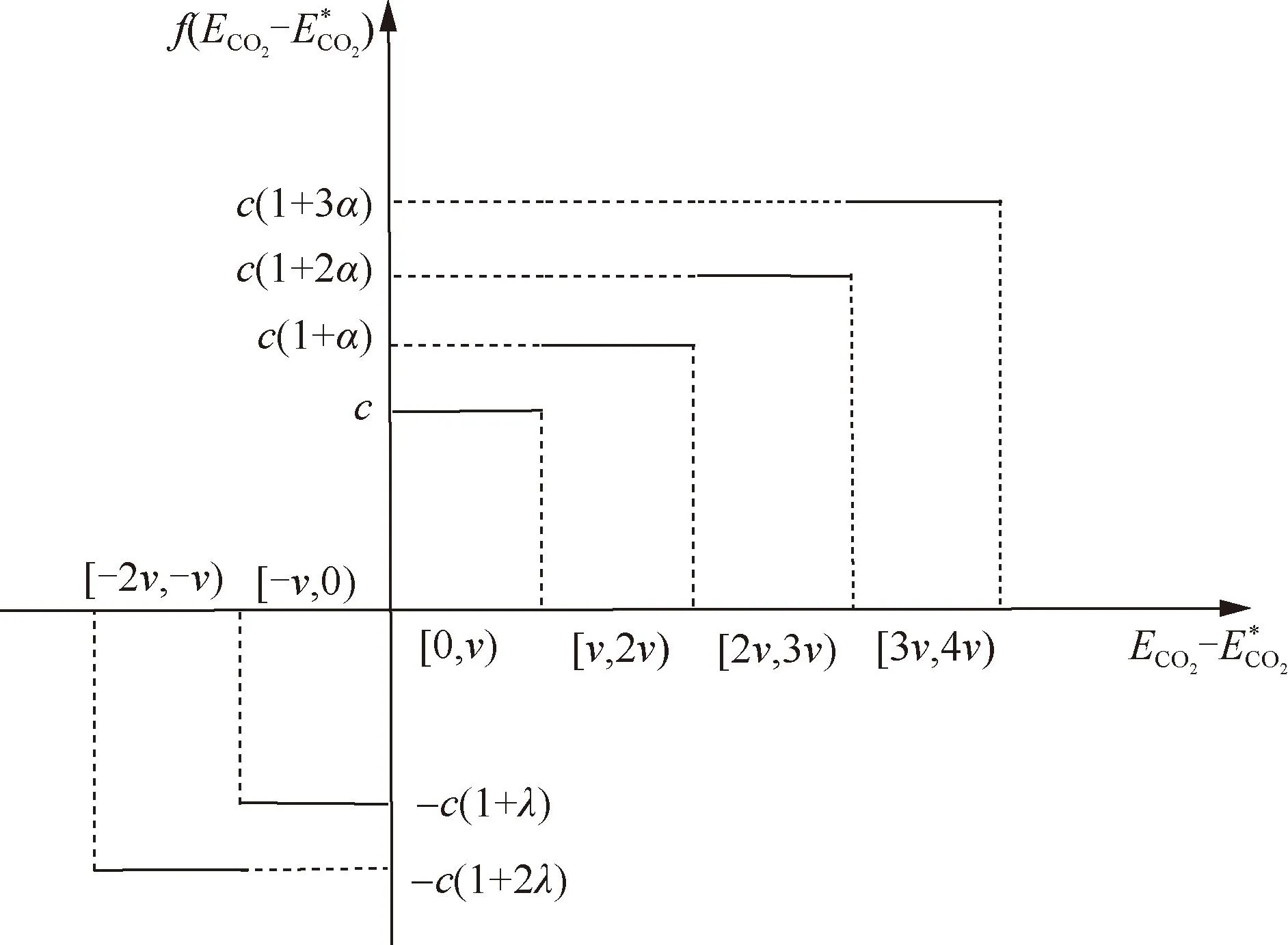
图2 碳交易价格与碳交易量关系Fig.2 Relationship between carbon trading price and carbon trading volume

阶梯型碳交易成本模型为:

(19)

式中:c为市场上碳交易基础价格;α为每个阶梯碳交易价格增长幅度;v为碳排放量区间长度。

4 考虑阶梯型碳交易的园区综合能源系统运行优化模型

4.1 目标函数

本文以LA合作联盟的日运营成本CLA最低为目标构建优化模型,其运营成本主要包括购售电成本、燃料成本、需求响应(可削减、可平移、可转移)补偿成本、碳交易成本及机组运维成本。

CLA=Cgrid+Ccurt+Cshift+Ctrans+
Cfuel+Com+CCO2

(20)

(21)

(22)

(23)

4.2 约束条件

1)功率平衡约束。

第i个LA在t时刻代理负荷区域内电功率平衡约束,可表示为:

(24)

(25)

2)能源网络传输功率约束。

考虑到能源网络运行的安全性,系统与能源供应网络之间的传输功率需要控制在安全范围内,各能源网络传输功率约束如式(26)-(29)所示。各LA与主电网交互约束,可表示为:

(26)

(27)

(28)

各LA与天然气网传输流量约束,可表示为:

Ggas,t,min≤Ggas,t≤Ggas,t,max

(29)

式中:Ggas,t、Ggas,t,max、Ggas,t,min分别为外部天然气网向园区系统传输的天然气流量及其上、下限。

3)机组出力约束。

园区综合能源系统的机组包括热电联产装置、光伏机组,各机组都需满足其出力运行上下限约束:

(30)

(31)

其中,热电联产机组消耗天然气量与输出电功率之间满足如下运行约束:

(32)

式中:Δt为每个调度周期的采样时间间隔;QLHV,ng为天然气的低位热值。

蓄电装置约束为:

(33)

(34)

(35)

Smin≤St≤Smax

(36)

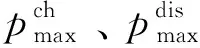
4)合作联盟内部约束。

多个LA合作时,须保持内部买卖总量平衡,对于某LA,买电和卖电不可同时进行,且不能超过允许的最大值,可表示为式(37)-(39)。为防止出现LA从电网或其他LA买电再转卖现象,约束如式(40)-(43)所示。

(37)

(38)

(39)

(40)

(41)

(42)

(43)

4.3 成本分配原则

合作博弈对于成本的分配问题,有核心、核仁、Shapley值等多种合作博弈解。分配的稳定性和合理性对于合作博弈及其重要,其中合作博弈的核心可能为空集,当核心不存在时,核仁分摊也无法应用,而Shapley值具有对称性、有效性、可加性、边际性4种性质,该方法是具有可行性和唯一性的合作博弈解,可以克服上述其他方法的局限。

Shapley值法可根据参与者对于联盟的边际贡献衡量参与者在联盟中的地位,从而对联盟的总成本进行分配[11],其体现了参与者在随机融入联盟的条件下,任一参与者对其进入联盟所作出边际贡献的期望收益值。参与者的期望收益可通过计算其边际贡献得到,即含该参与者的联盟特征函数减去不含该参与者的联盟特征函数所得差额为该参与者的边际贡献,如式(44)所示。结合概率理论统计,可分别计算每个参与者在每个子联盟中对整个联盟运营成本降低的边际贡献,建立基于Shapley值法的具有唯一解的成本分配模型,如式(45)所示。

Mi=Call(s)-Call(si)

(44)

(45)

式中:Mi表示第i个LA对联盟s的边际贡献;Call(si)为联盟s中除去第i个LA剩下LA形成合作联盟的运营成本;|s|为联盟s中参与人的数目;n为总联盟中参与者数目。

5 算例分析

本文以上海某业态混合型园区为研究对象进行案例分析,园区内包括工业用户、商业用户和居民用户。假设该综合园区内有3个LA,分别为工业、商业和居民用户聚合商。各LA分别备有分布式电源及储能装置,其中,工业用户配有热电联产设备,商业用户配有光伏及蓄电池,居民用户配有光伏设备。为进行比较分析,各LA之间在合作联盟运营和非合作运营2种情景下分别进行优化和结果对比,如图3所示。非合作运营模式下,各LA之间以自身运营成本最低为目标,对其柔性资源进行响应优化,相互间不存在能源共享,因此也不存在成本分配问题。合作联盟运营模式下,各LA之间存在能源交互,保证合作联盟整体运营成本最低。为使用Shapley值法进行成本分配,考虑的潜在合作模式包括:LA1与LA2合作、LA1与LA3合作、LA2与LA3合作及LA1、LA2、LA3三者共同合作。

图3 多个LA非合作和合作联盟运营示意图Fig.3 Image of non-cooperative and cooperative operations of multiple LAs

5.1 参数设置

在本文算例中,LA与电网和用户之间的购售电价及峰、平、谷时段划分如表1所示[13, 22-25],碳交易参数设定如表2所示[19]。

表1 能源价格参数Table 1 Energy price parameters

表2 碳交易参数设定Table 2 Carbon trading parameter setting

用户需求响应需提前与LA签订合同,包括补偿价格、响应量和响应时间划分。负荷削减合同参数设置如表3所示[17],可转移负荷合同设置如表4所示[22],可平移负荷合同设置如表5所示[26-28]。

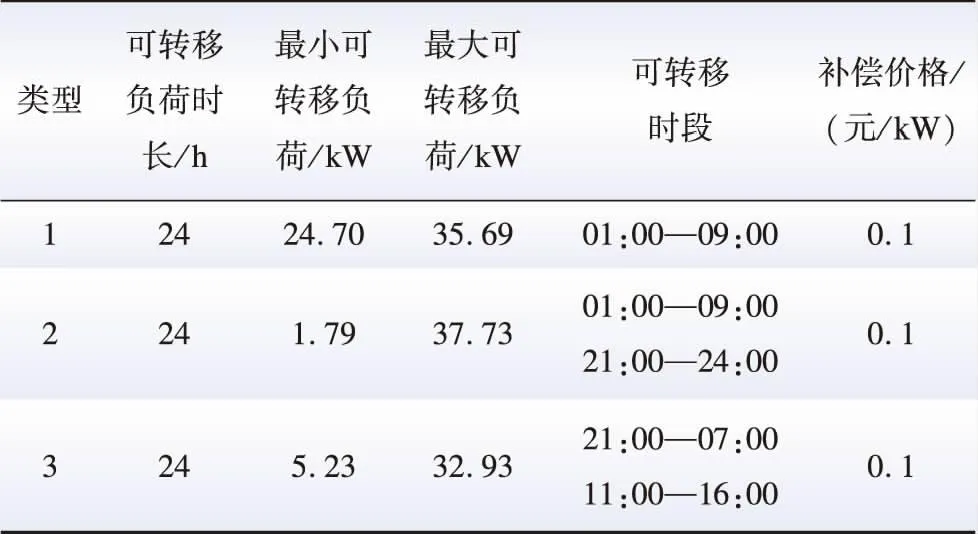
表4 可转移负荷参数Table 4 Transferable load parameters

表5 可平移负荷参数Table 5 Shiftable load parameters

园区内各用户配备不同类型的分布式能源设备,在运行过程中存在相应约束,其功率限制、维护成本等参数设置如表6所示[29-30]。

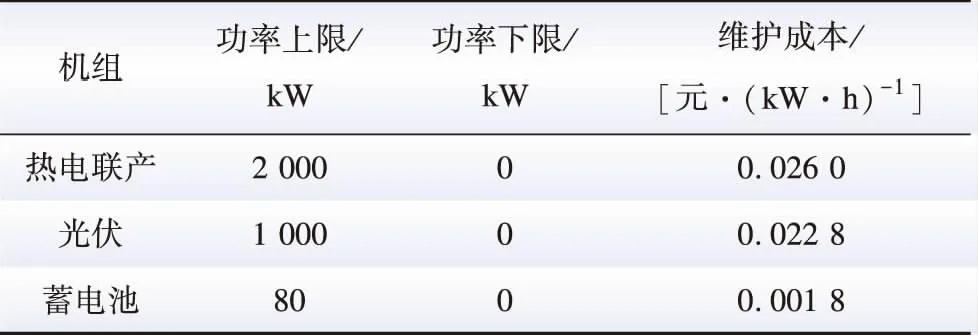
表6 分布式发电单元运行参数Table 6 Operating parameters of distributed generation units

5.2 运行策略对比

2种模式下3个LA的运行策略对比如图4所示,可以看出,LA相互合作下,外购电量明显降低。

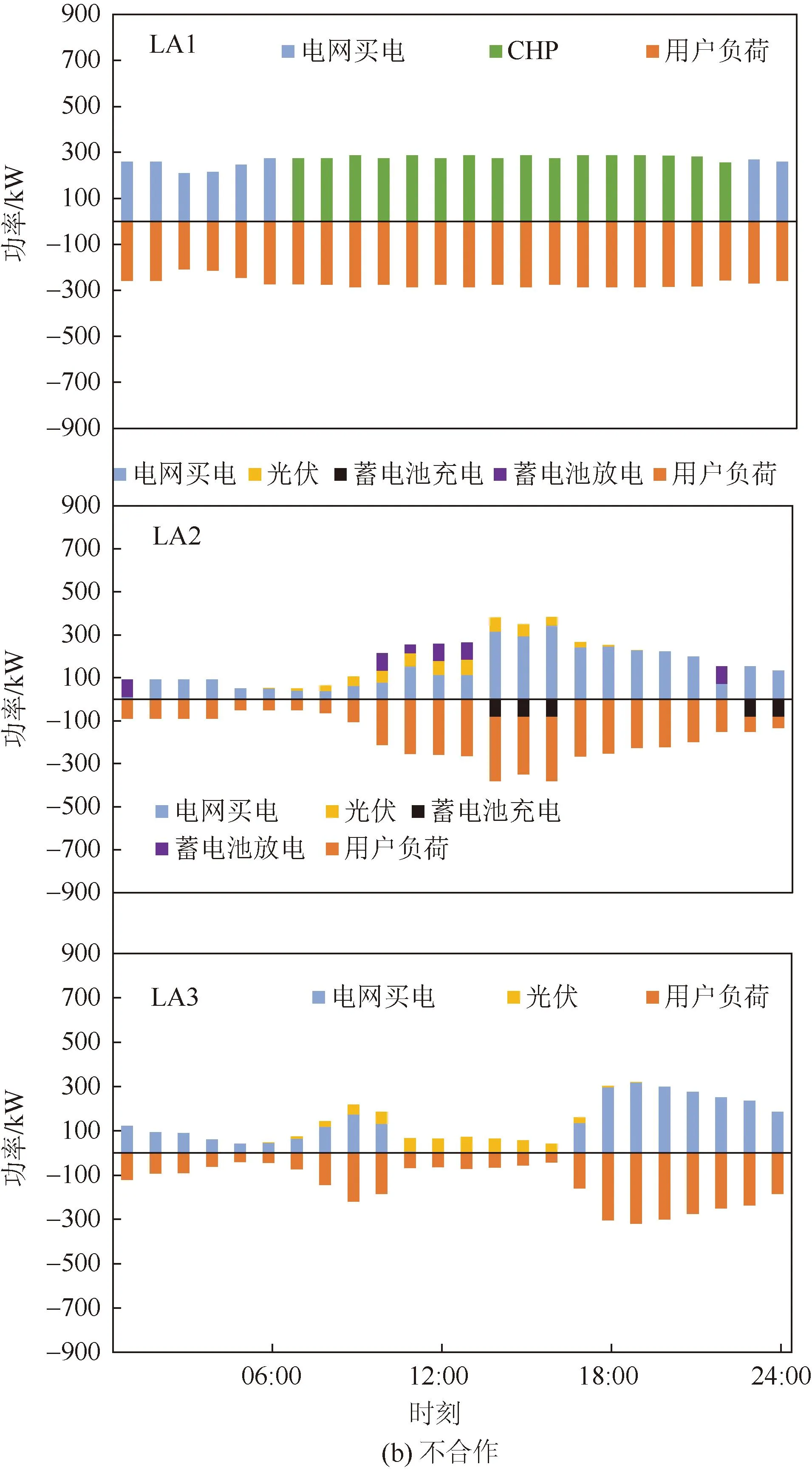
图4 2种运营模式下的运行策略对比Fig.4 Comparison of operation strategies under two operation modes

由图4(a)可见,合作模式下,由于LA1、LA2、LA3所代理用户类型不同,用电特性差异较大,存在互补特性,因此,不同LA之间存在电量交易。LA1主要在电价低谷时通过电网买电,其余时间依靠CHP设备进行供电,并协助其他LA在电价高时减少购电量。由于LA3用电高峰时段与LA2不同,所以存在LA1错峰售电的情况,以保证整体利益最优。在08:00、09:00-22:00,LA1分别向LA3和LA2售电;LA2在09:00-21:00处于用电高峰期,从LA1买电量明显增多;LA3在用电高峰主要依靠从LA1、LA2买电及自身安装的光伏设备进行供电,其余时间依赖电网。蓄电池设备则在电价引导下于23:00-24:00进行充电,在22:00以及其他用能时段放电满足负荷需求。

由图4(b)可以看出,由于各LA之间没有电能交互,各用户仅依靠自身配备的分布式电源以及外部电网满足自身的负荷需求。LA1主要是在电价低谷时期从电网买电,其他时间均依赖CHP进行发电;LA2、LA3主要依靠光伏出力,在其新能源出力不足时再选择电网购电;LA2的储能设备利用电价差异,在电价较低时进行充电,在负荷需要较高时进行放电。

5.3 需求响应策略对比

2种模式下的响应策略对比如图5所示。在合作运营模式下,不同类型用户参与需求响应前后负荷曲线对比如图5(a)所示。从01:00-08:00时段负荷削减程度来看,LA1>LA3>LA2,这是由于此时段LA1代理用户与LA2和LA3代理的用户相比负荷基数较大,存在较大削减能力;在09:00-24:00时段,随着LA2负荷水平不断增大,联盟内部缺电量逐渐增多,促使各LA2开始增大削减负荷的强度。总体来说,LA1将负荷转移到23:00-05:00,LA2将负荷转移到23:00-06:00、14:00-15:00等时段,LA3则将负荷转移到23:00-07:00电价最低时段,通过削峰填谷降低用能成本。

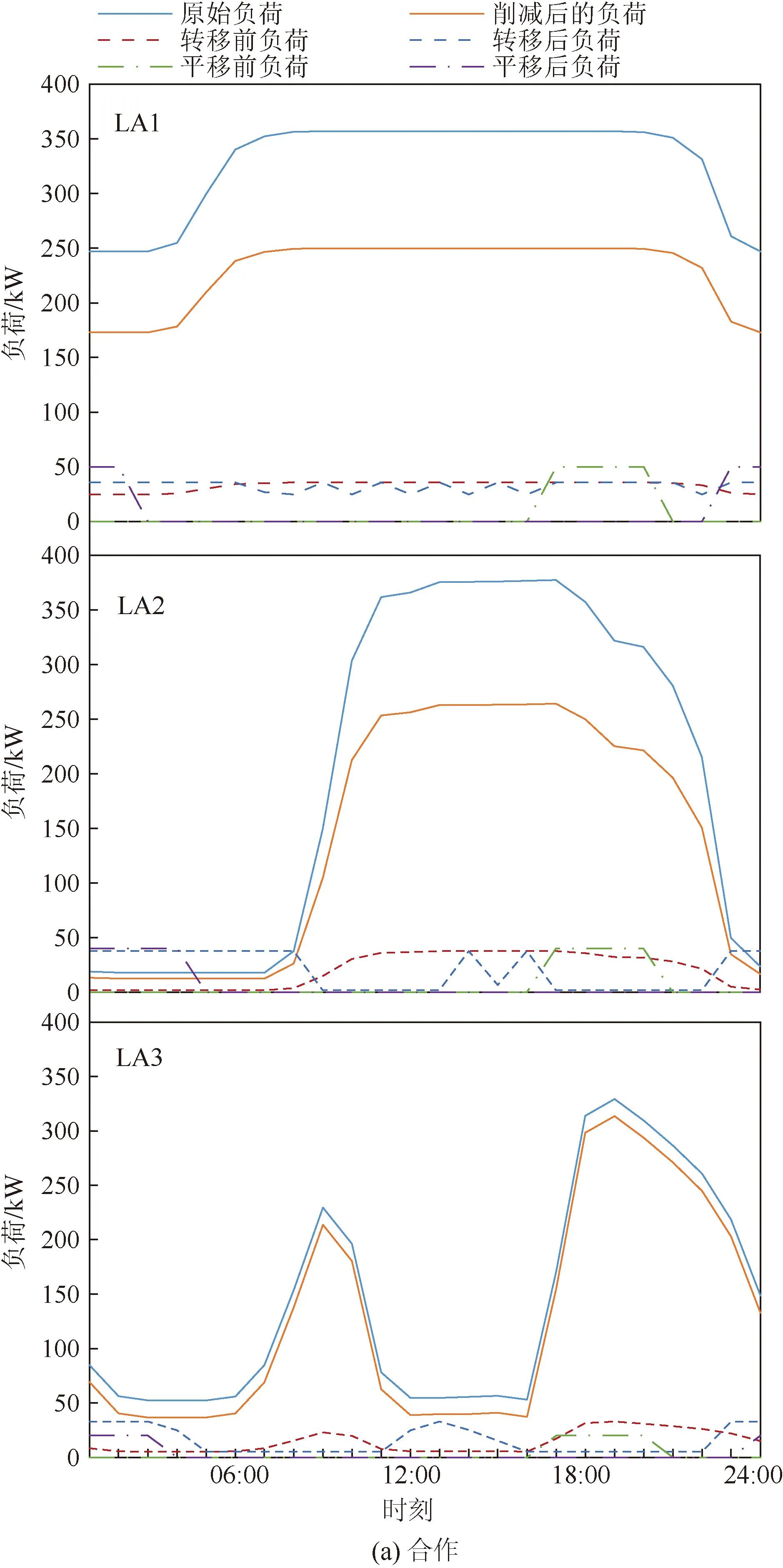
图5 2种运营模式下的需求响应策略对比Fig.5 Comparison of demand response strategies under two operation models

由图5(b)可以看出,在非合作运营模式下,负荷削减趋势与合作博弈运营方式的优化结果并无明显差异,这是由于削减能力主要与用户用能特性相关,各类用户负荷削减程度与削减合同的一次项系数和二次项系数有关,而系数的确定则依赖于用户负荷曲线。可平移负荷在电力价格的驱动下,由峰时段转移到23:00-04:00期间内的不同时段,一方面,削峰填谷,促进电力系统稳定运行;另一方面,可以节约部分电费,降低各LA运营成本。可转移负荷在非合作的运营模式下与合作联盟运营模式略有不同,主要是降低各峰时段负荷,将其转移到23:00-08:00、14:00-16:00低谷时期,平抑负荷波动,实现错峰用电。

5.4 碳交易对比分析

图6为2种运营模式下的碳排放及碳排放权交易情况。从图6中可以看出,合作联盟运营模式下,LA1碳排放量较非合作运营模式提高25.76%,而LA2、LA3的碳排放量小于非合作的运营模式,分别降低了3.91倍以及2.24倍,这是由于合作联盟运营主旨亦在降低三者碳排放总和,从而降低碳排放成本,整体来看,系统总碳排放量相较于非合作运营模式,减少40.09%;相应地,碳排放权的购买也随之减少17.63%。总体碳交易收益相较于非合作运营模式提高1.08倍,有效地降低了整个合作联盟及联盟个体的运营成本。

图6 2种运营模式下的碳交易策略对比Fig.6 Comparison of carbon trading strategies under two operating models

5.5 运营成本结果对比和成本分配策略

1)运营成本结果对比分析。

不同运营模式下联盟整体成本如表7所示,负值代表收益。可见,合作博弈模式下,需求响应成本更高,响应资源得到深一步挖掘。其次,购能成本更低,而燃料成本更高,这是因为内部合作加大了本地设备出力和自平衡,降低了外部购能需求。此外,碳交易收益大幅提升,整体碳收益增加51.98%,说明联盟合作可有效降低整体碳排放量,促进园区低碳经济运行。

表7 不同运营模式下联盟整体成本对比Table 7 Comparison of overall affiliate costs under different operating models 元

2)合作博弈下的成本分配策略。

为保证合作博弈运营模式的合理性,Shapley值法从公平性角度出发,“论功行赏”将成本按照边际贡献进行分配,也就是说,按照此分配策略,参与者i所应分摊的成本等于该参与者对每一个其所参与联盟的边际贡献的平均值。通过式(44)计算可得出参与者对不同联盟的边际贡献,结果如表8所示,基于式(44)并结合式(45),计算可得出应用Shapley值法分配后的各LA运营成本,结果如表9所示。相较于非合作运营,合作模式下,联盟整体成本降低18.72%,LA1、LA2、LA3成本分别降低22.39%、14.95%以及17.61%。

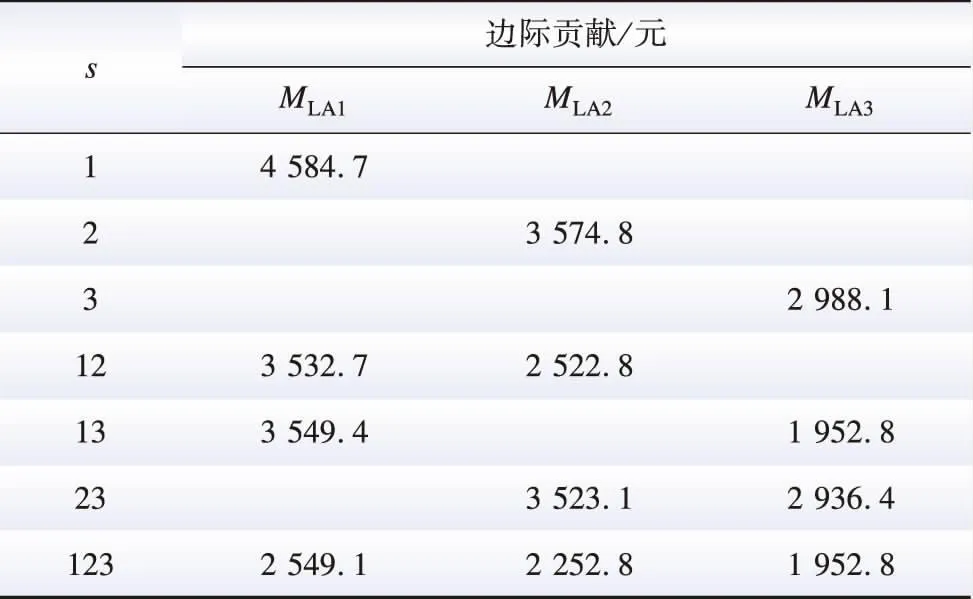
表8 潜在联盟策略边际贡献度分析Table 8 Analysis of the marginal contribution of potential alliance strategies

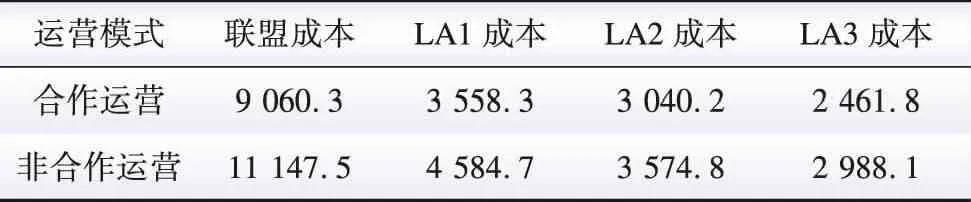
表9 各运营模式成本分析Table 9 Cost analysis of each operation mode 元

6 结 论

本文提出了基于能源互济和碳交易的多类型LA合作联盟运营机制,综合考虑了不同类型用户柔性负荷互补和响应特性。以联盟整体运营成本最低为目标,提出联合优化模型,并利用合作博弈Shapley值法对成本进行合理分配。可得出以下结论:

1)利用LA聚合园区内不同类型用户,实现了柔性负荷资源参与需求响应;同时通过LA内部联盟的能源共享互济,有效挖掘了不同用能模式下的负荷互补特性。相比于各LA互相独立运作,整体联盟成本降低达18.72%。

2)通过LA之间的联盟合作,可明显降低碳排放量,通过整合单体用户加入碳交易市场,外界购入的碳排放权减少17.63%,可实现联盟整体碳收益最大化,整体碳收益增加51.98%,促进园区低碳经济运行。

3)通过合作博弈的Shapley值法构建成本分配模型,实现了合作联盟整体成本的公平、合理分配,各LA成本分别降低22.39%、14.95%、17.61%,从而有效提升了各LA参与合作的积极性,从而促进联盟整体稳定性。