基于合作博弈的城市楼宇集群分布式储能容量共享

冀瑞强,胡健,张晓杰

(1．山东理工大学电气与电子工程学院,山东省淄博市 255000;2．山东理工大学经济学院,山东省淄博市 255000)

0 引 言

随着“双碳”目标贯彻落实工作的推进及可再生能源发电技术的进步,以屋顶光伏为代表的分布式可再生能源发电设备在城市社区、工农业园区的应用日益普及[1-3]。配置储能可以解决光伏等可再生能源出力不可控问题[4],但受储能技术及商业模式的影响,现阶段储能设备的投资与维护成本较高[5-6],且可再生能源出力及负荷需求的不确定性使储能设备的实际利用率偏低[7]。

共享储能是共享经济环境下出现的一种新型储能应用模式[8-10]。通过储能设备所有权与使用权的分离实现储能资源的共享使用,可提高储能利用率,降低储能设备的投资与运行成本。根据储能资源所有权不同,可将共享储能分为公共储能共享、自有储能共享[11]。公共储能共享是指由一个或多个集中式储能设备为多个用户提供储能服务[12]。文献[13]通过建立集中式共享储能电站为工业用户提供用能存储服务,实现了工业园区的经济运行。公共储能共享比较适用于用户均没有配置储能的情况,且集中式储能设备往往由第三方储能服务商投资建设和运营。对于已经配置储能的用户,当其储能设备利用率较低时,会倾向于将自身部分储能资源提供给没有储能的用户使用,即自有储能共享,从而提高储能利用率并摊薄初始投资成本。本文将主要讨论这种储能共享模式。

文献[14]提出了一种含优化匹配功能的分布式储能线上共享交易模式,保证了参与共享的用户具有长期的非负效益。文献[15]提出了一种储能容量共享拍卖机制,通过确定用户与公共用电设施共享储能的容量比例,实现了储能资源的高效利用。文献[16]提出了一种储能容量共享迭代清算方法,解决了多个储能拥有者与多个储能需求者的共享问题。上述基于拍卖机制或迭代清算的储能共享方法都是采用非合作博弈理论设计的共享机制。然而在储能资源共享环境下,用户之间不再是竞争博弈的关系,而是以效益最大化或成本最小化为目标的一种合作博弈关系。参与储能共享的用户构建适当形式的合作联盟,通过信息共享和协商共识可获得超过非合作博弈情景的合作剩余。文献[17]采用合作博弈理论证明了用户之间储能合作共享的可行性。

基于合作博弈的分布式储能容量共享不仅涉及联盟整体利益最优问题,还涉及联盟合作剩余分配问题。现阶段,联盟合作剩余分配多采用Shapley值法、核仁法等方法[18-19],但计算复杂程度会受联盟主体数量影响。Raiffa解法继承了Shapley值法按边际贡献分配的思想,是一种考虑各主体利益的合作剩余分配方法[20-21]。对含n个主体(n> 2)合作联盟的合作剩余分配问题,所需考虑的合作策略不超过n+1个,远低于Shapley值法的2n-1个[22-23]。但Raiffa解法假定每个主体参与联盟时的投入相同,会因忽略主体间投入的差异而出现分配不公平的现象。因此,考虑已配置储能用户和未配置储能用户在前期储能设备投入上的差异对经典Raiffa解法进行改进,用于自有储能共享模式下合作剩余的分配将是有意义的工作。

综上所述,本文以配置光伏和储能设备的城市楼宇集群为研究对象,基于合作博弈理论提出了一种城市楼宇集群分布式储能合作共享模型,并采用改进Raiffa解法对联盟合作剩余进行分配。

1 基于合作博弈的城市楼宇集群分布式储能容量共享

楼宇集群是城市配电网服务的主要对象。楼宇集群由配置和未配置储能设备的商业、办公及居民楼宇组成,各楼宇在物理上都与配电网相连接。一种针对楼宇集群的自有储能共享框架见图1,并假设配置储能楼宇的储能容量可全部参与共享。各楼宇可通过合作组成联盟,共享集群内的全部储能资源。储能共享平台作为配电网为协助楼宇实现储能共享而建立的非盈利性虚拟平台,具有汇集决策信息、撮合共享合约、组织合作剩余分配等功能。

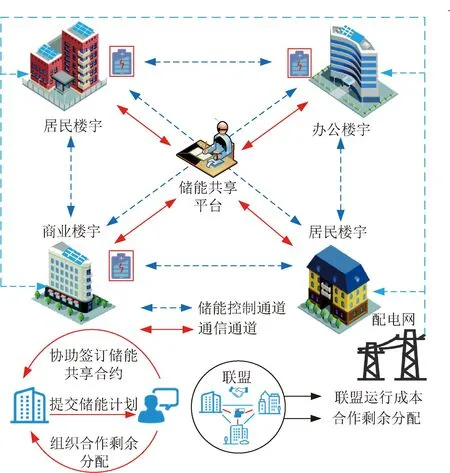
图1 城市楼宇集群分布式储能容量共享框架Fig.1 Capacity sharing framework for distributed energy storage of urban building cluster

楼宇集群分布式储能资源共享过程如下:

日前,各楼宇根据基础性负荷、分时电价、可调控负荷与可再生能源预测值,制定储能容量的分时使用计划,并通过通信通道上传至储能共享平台。储能共享平台汇集楼宇储能资源的可共享或需求信息,协助各楼宇签订储能共享合约。

日中,楼宇通过储能控制通道对经共享获得的储能资源进行充放电操作。在可再生能源出力富余时段或谷时电价时段进行充电,在可再生能源出力不足时段或峰时电价时段进行放电。

日后,储能共享平台计算楼宇集群因储能共享带来的合作剩余,并根据各楼宇对联盟效益的贡献,组织楼宇进行合作剩余的分配。

经过上述共享过程,配置储能楼宇因储能资源共享,可提高储能设备利用率,降低楼宇集群用能成本。未配置储能楼宇因储能资源共享,充放电决策更加灵活,可促进楼宇可再生能源就地消纳。

2 城市楼宇集群分布式储能容量共享模型

2.1 目标函数

在分布式储能容量共享过程中,各楼宇通过合作组成联盟共享集群内的全部储能资源,并以联盟运行成本最低为目标函数:

(1)

1)购电成本。

假定楼宇不具备余电上网能力。楼宇购电成本:

(2)

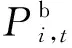
2)碳排放成本。

支撑楼宇负荷的电力来源于自身光伏发电和电网购电。不考虑光伏设备制造环节的碳排放因素,楼宇电力碳排放主要来源于电网购电部分。碳排放成本[24]:

(3)

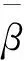
3)弃光惩罚成本。

储能容量共享可以提高光伏就地消纳率。为促进光伏就地消纳,可将弃光情况计入成本,楼宇弃光惩罚成本[25]:

(4)

4)可控负荷效益。

考虑楼宇可控负荷,如:可调度的电器设备(shiftable electrical appliances, SEA)、暖通空调(heating ventilation and air conditioning, HVAC)、灵活商业服务(flexible commercial service, FCS)耗能所带来的效益,建立可控负荷效益模型度量楼宇用电满意度[26]。楼宇i内的可控负荷效益:

(5)

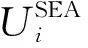
(1)SEA效益函数。

SEA实际耗电功率与预设功率会产生偏差,影响用户用能体验。根据楼宇中SEA实际耗电功率与预设功率,SEA效益函数可描述为用户对SEA实际耗电的满意程度,即:

(6)

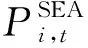
(2)HVAC效益函数。

根据室内温度、最佳室内温度预设值,HVAC效益函数可描述为用户对室内温度的满意程度,即:

(7)

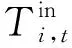
其中,当前时段室内温度与室外温度、前一时段室内温度有关,具体如下:

(8)

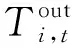
(3)FCS效益函数。

根据FCS耗电带来的经济效益,FCS效益函数可描述为用户对FCS耗电的满意程度,即:

(9)

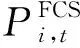
5)集群储能使用成本。

由于集群整体的充放电行为与各楼宇的充放电行为并不一致,而集群储能使用成本主要取决于集群整体的充放电行为,因此集群储能使用成本可表示为:

(10)

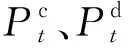
2.2 约束条件

1) 楼宇经共享获得的储能约束条件:

(11)

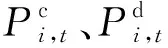
2) 集群储能约束条件:

(12)

式中:Et为t时段集群储能存储的电量;Emax、E0分别为集群储能设备存储电量上限和初值;Pmax为集群储能整体充放电功率限额;ηc、ηd分别对应总充放电效率;At、Bt为0、1变量。

经过分布式储能容量共享,集群全部储能设备存储的电量与各楼宇经共享得到储能资源存储的电量应满足:

在一次新闻发布会上，国家林草局三北防护林建设局局长张炜介绍说，四十年来，三北工程取得了举世瞩目的辉煌成就——累计完成造林保存面积二千九百一十九万公顷，工程区森林覆盖率由1977年之前的百分之五提高到百分之十三以上，森林蓄积量由七亿立方米增加到二十一亿立方米。三北工程为改善三北地区生态环境，促进经济社会健康发展做出了重要贡献。

(13)

集群储能设备整体充放电功率限额与楼宇的充放电功率限额需满足以下约束:

(14)

3) 楼宇功率平衡约束:

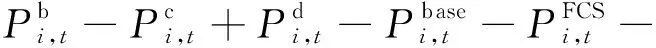
(15)

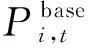
4) 楼宇光伏实际调度出力约束。

楼宇光伏实际调度出力应小于等于其光伏输出功率:

(16)

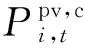
5) 楼宇弃光量约束。

根据国家能源局印发的《清洁能源消纳行动计划(2018-2020年)》, 2020年弃光率要低于5%。本文按弃光比例达到5%时开始计算弃光惩罚成本。楼宇弃光量约束:

(17)

(1) SEA实际用电计划功率约束:

(18)

(2) 为创造舒适的工作环境,室内温度需限制在恰当的范围内,以确保室内温度被用户所接受:

(19)

(3) FCS耗电功率约束:

(20)

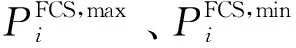
2.3 模型求解

采用交替方向乘子法(alternating direction method of multipliers,ADMM)将楼宇集群分布式储能容量共享问题转化为集群储能运行优化问题和楼宇运行优化问题。

对耦合等式约束式(13)引入拉格朗日乘子αt和惩罚因子ρ,得到目标函数式(1)的增广拉格朗日函数:

(21)

根据ADMM算法,对式(21)进行分解,得到集群储能运行优化模型、楼宇运行优化模型,具体表达如下:

1) 集群储能运行优化模型:

(22)

2) 楼宇运行优化模型:

(23)

ADMM算法中拉格朗日乘子αt更新迭代过程如式(24)所示:

(24)

式中:k为当前迭代次数。

迭代收敛判断依据如式(25)所示:

(25)

式中:kmax为最大迭代次数;ξ为收敛阈值。

楼宇集群分布式储能容量共享模型的ADMM算法具体求解步骤如图2所示。

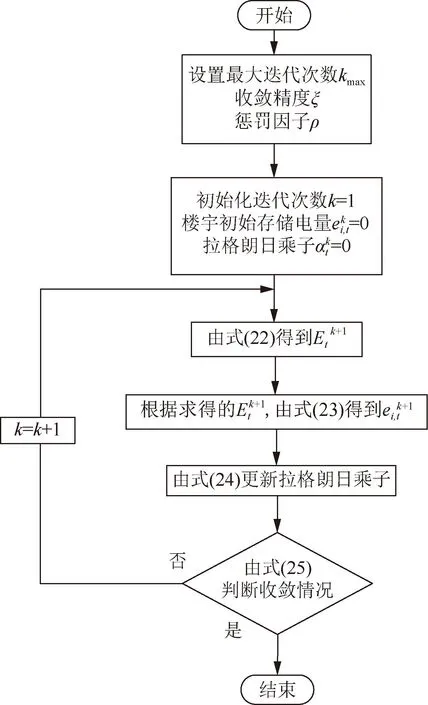
图2 ADMM算法求解步骤Fig.2 ADMM algorithm solving steps

3 联盟合作剩余分配

楼宇有意愿参与合作联盟的前提是通过储能共享可降低楼宇集群运行成本,获得显著的合作剩余,并对合作剩余在楼宇间进行公平合理的分配。本文采用考虑储能初始投入的改进Raiffa解法对联盟合作剩余进行分配。

3.1 基于Raiffa解法的联盟合作剩余分配

假设N栋楼宇组成联盟进行储能共享获得的合作剩余为B。基于Raiffa解法的联盟合作剩余分配步骤如下[20-21]:

1)确定合作剩余分配下限。

假定楼宇i不参与储能合作共享,利用其他N-1栋楼宇组成联盟的合作剩余计算合作剩余分配值的下限:

(26)

式中:bi为楼宇i未参与合作,其余N-1栋楼宇合作组成联盟时的合作剩余。

2)确定合作剩余分配上限。

将楼宇i的边际贡献,即N栋楼宇储能共享的合作剩余与楼宇i不参与储能共享的合作剩余的差值,作为楼宇合作剩余分配值的上限:

(27)

3)确定合作剩余分配值。

基于合作剩余分配上、下限,确定楼宇i和其他N-1栋楼宇的合作剩余分配值:

(28)

依次考虑每栋楼宇的边际贡献后,取平均得到楼宇i的合作剩余分配值:

(29)

可以看出,采用Raiffa解法对联盟合作剩余进行分配不仅继承了Shapely值法按边际贡献分配的思想,且所需考虑的合作剩余量为N+1个,即:N栋楼宇参与储能共享时的合作剩余B以及楼宇i不参与储能共享而其他N-1栋楼宇进行储能共享时的合作剩余bi。而若采用Shapley法需计算N栋楼宇在所有合作组合下的合作剩余,共计2N-1个[22],当楼宇数量N很多时,Raiffa解法计算量明显减少。

但Raiffa解法中假定每栋楼宇参与联盟时的投入相同,现实情况并非如此。当忽略主体投入差异,而对各楼宇按照等值投入权重进行合作剩余分配,不可避免会出现分配不公平现象。因此,需在考虑各主体投入差异的前提下,对Raiffa解法进行改进。

3.2 考虑储能初始投入的改进Raiffa解法

在自有储能共享模式下组建合作联盟的主体包括已配置储能楼宇和未配置储能楼宇。联盟的共享储能资源来源于已配置储能的楼宇,各主体对联盟储能资源的前期投入是不同的,所以在合作剩余分配中应考虑各主体的前期投入的差异。

1)合作剩余分配权重改进。

以楼宇自配储能设备的容量为依据,改进楼宇合作剩余分配权重:

(30)

式中:ei,ES为集群中自有储能楼宇的储能最大容量。

所有楼宇合作剩余分配权重应满足:

(31)

改进前后楼宇合作剩余分配权重之差为:

(32)

式中:ΔRi为考虑楼宇自配储能的权重调整量,且需满足:

(33)

2)合作剩余分配值调整。

利用ΔRi对合作剩余分配值进行调整,可得:

Δci=ΔRiB

(34)

则经调整后的楼宇合作剩余分配值:

c′i=ci+Δci

(35)

因此,楼宇经分布式储能容量共享后的最终运行成本为:

(36)

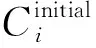
基于改进Raiffa解法的楼宇集群分布式储能容量共享合作剩余分配及楼宇最终运行成本具体计算过程见附录A图A1。

4 算例分析

4.1 算例及参数

以含一栋商业楼宇、两栋办公楼宇、三栋居民楼宇的楼宇集群为研究对象,各楼宇储能及光伏配置情况见表1。6栋楼宇中,商业楼宇拥有FCS和HVAC,办公楼宇1、2拥有HVAC和SEA,居民楼宇1-3拥有SEA。储能设备的功率损耗成本系数取0.10元/kWh[26];分时电价、可控负荷主要参数、楼宇光伏输出功率、室外温度、基础性负荷分别见附录A表A1、A2、图A2、A3[26-27];碳排放价格取56.50元/t[28];电网平均碳排放因子取0.57t/MWh(CO2)[29];单位弃光惩罚成本取0.6元/kWh[30]。

表1 楼宇储能、光伏配置情况Table 1 Configuration of energy storage and photovoltaic

为验证所提模型的有效性,本文设置以下两种场景。

场景1：各楼宇储能设备独立运行,不进行分布式储能资源共享;

场景2：各楼宇通过合作组成联盟共享集群内的储能资源。

通过MATLAB 2020a平台Yalmip工具箱对约束条件和目标函数进行建模,调用Mosek求解器和Gurobi求解器求解。

4.2 结果与分析

基于ADMM算法的城市楼宇集群分布式储能容量共享模型的求解收敛过程见图3。可以看出,经迭代191次后收敛精度达到预设值0.01,说明所提方法具有较好的收敛性。

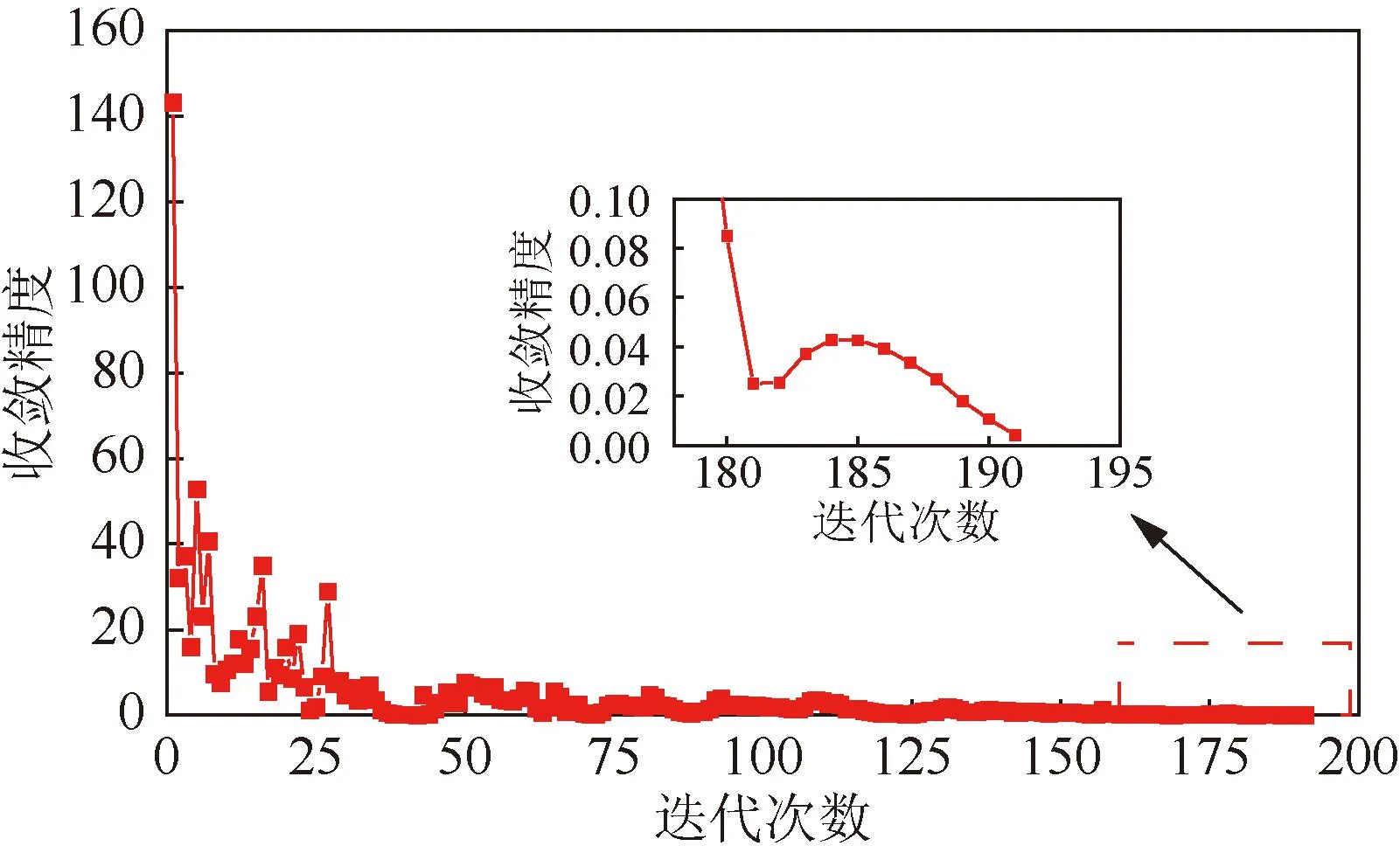
图3 基于ADMM算法的迭代收敛过程Fig.3 Iterative convergence process based on ADMM algorithm

4.2.1 储能使用情况分析

场景1、2下楼宇集群储能资源使用情况见图4、5。

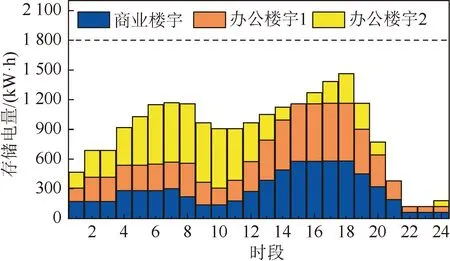
图4 场景1 楼宇集群储能使用情况Fig.4 Energy storage usage of building cluster in scenario 1

由图4可以看出,场景1下商业楼宇、办公楼宇1的储能设备存储的电量在全天24个时段内均低于其储能容量上限,且在0-7时段的存储电量均低于储能容量上限的50%。办公楼宇2的储能设备存储电量在6-10时段达到储能容量上限,但在13-24时段存储电量低于储能容量上限的50%。可知商业楼宇、办公楼宇1存在部分时段储能容量闲置的情况,办公楼宇2存在部分时段储能容量不足、部分时段储能闲置的情况。

结合楼宇存储电量情况,以及集群储能设备可存储的最大电量,给出集群储能利用率:

(37)

可得,楼宇集群整体储能资源利用率在场景1下仅为49.08%,储能利用率较低。

由图5可以看出,场景2下拥有储能资源的楼宇出让储能设备的使用权,与其他楼宇组成联盟合作共享使用集群内全部的储能资源。没有配置储能设备的居民楼宇1-3通过储能资源共享,也拥有了联盟内储能资源的使用权,因此楼宇集群整体储能资源利用率达到67.20%,且在6-9、12-18时段集群储能整体存储电量接近或达到储能容量上限。

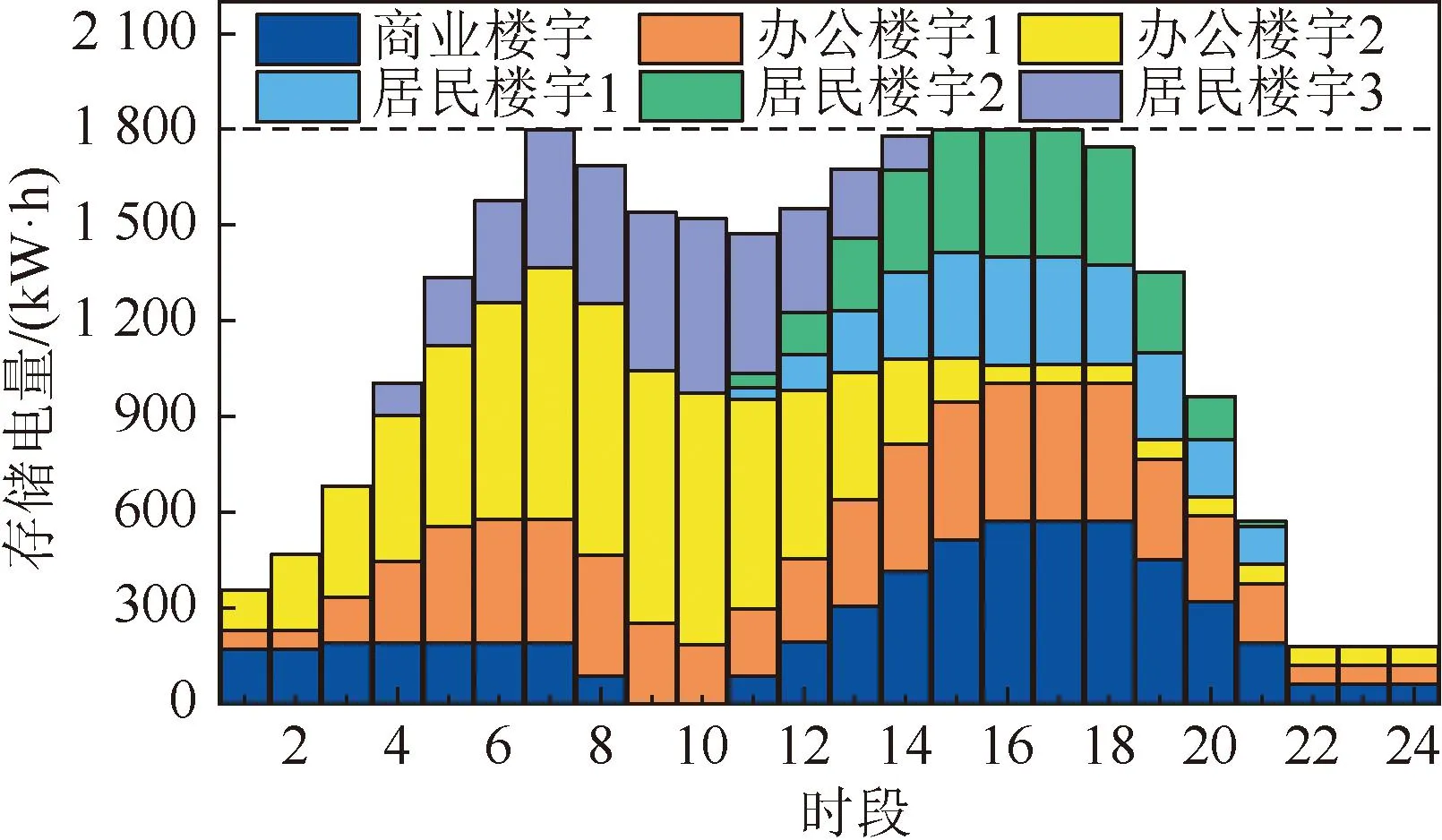
图5 场景2 楼宇集群储能使用情况Fig.5 Energy storage usage of building cluster in scenario 2

场景2下居民楼宇1-3、办公楼宇2使用共享储能资源的情况见图6-9。居民楼宇1、2配置了光伏发电装置,由图6、7可以看出,为提高光伏就地消纳率,其利用共享获得的储能资源在光伏出力大于负荷的11-16时段进行充电,在光伏出力不足和电价较高的18-22时段利用共享获得的储能资源进行放电,既促进了可再生能源的就近消纳,又降低了购电成本。

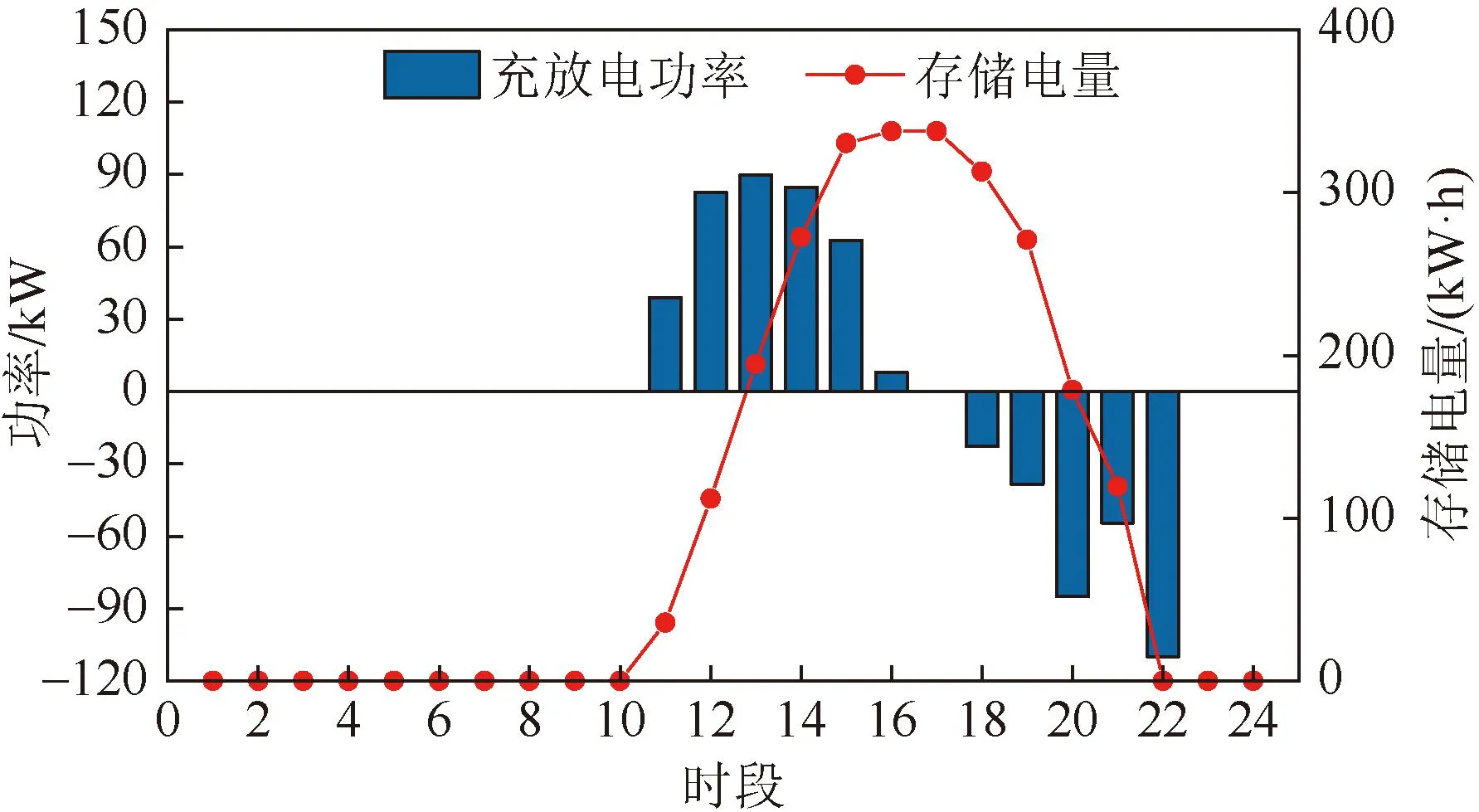
图6 居民楼宇1储能使用情况Fig.6 Energy storage usage of residential building 1

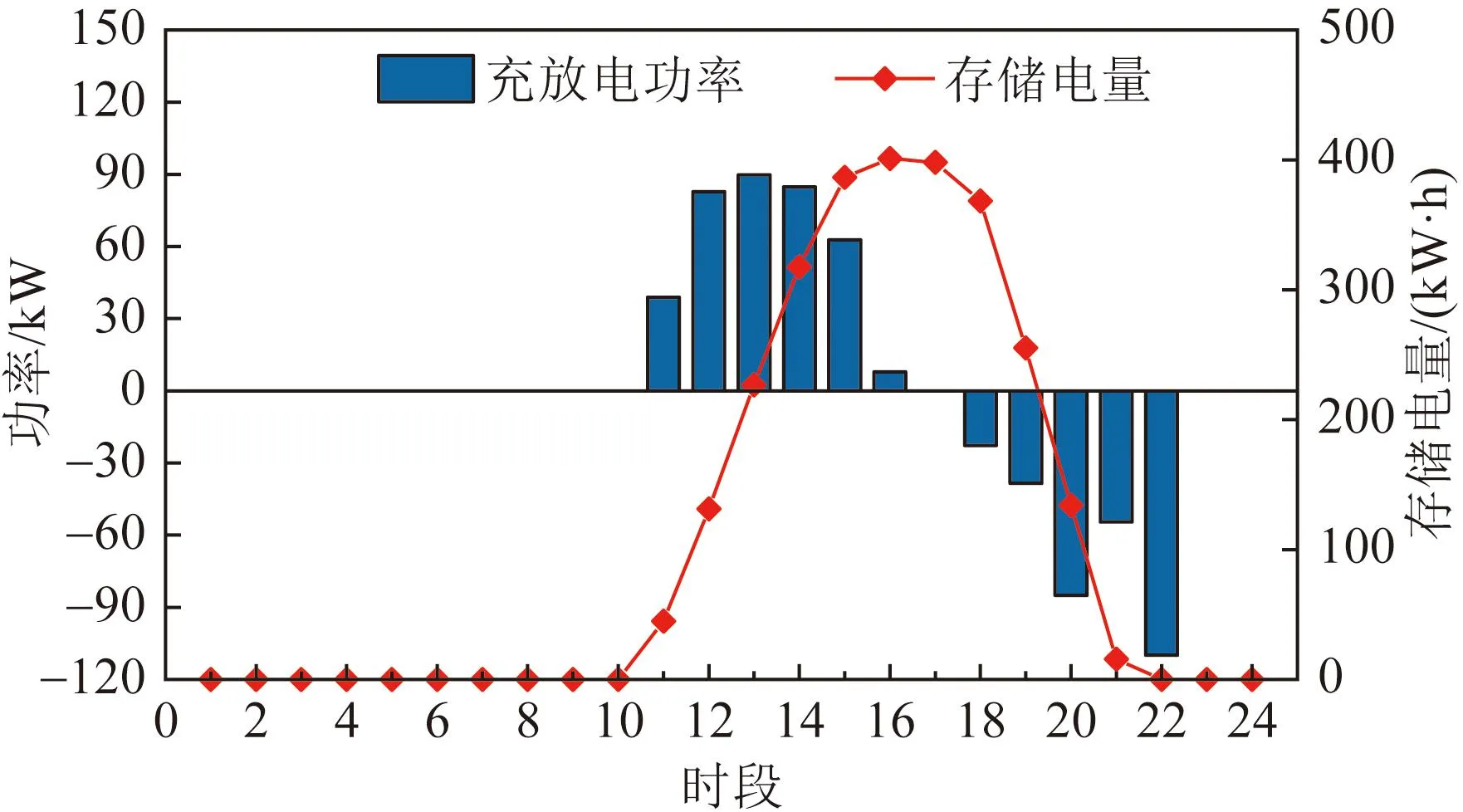
图7 居民楼宇2储能使用情况Fig.7 Energy storage usage of residential building 2

居民楼宇3没有配置光伏发电装置,不需利用储能装置平衡自身源荷在时间尺度上的差异。由图8可以看出,其借助共享获得的储能资源在谷时电价的4-7时段和平时电价的9、10时段进行充电,在峰时电价的10-15时段进行放电,以此来实现电费的峰谷价差套利,降低用能成本。由图9可以看出,在电价的较低的1-7时段,办公楼宇2可利用共享后的储能资源进一步满足自己的充放电需求,继而在7-10时段的存储电量远超过其自有储能容量上限600 kWh。

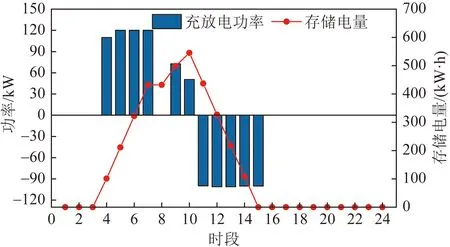
图8 居民楼宇3储能使用情况Fig.8 Energy storage usage of residential building 3

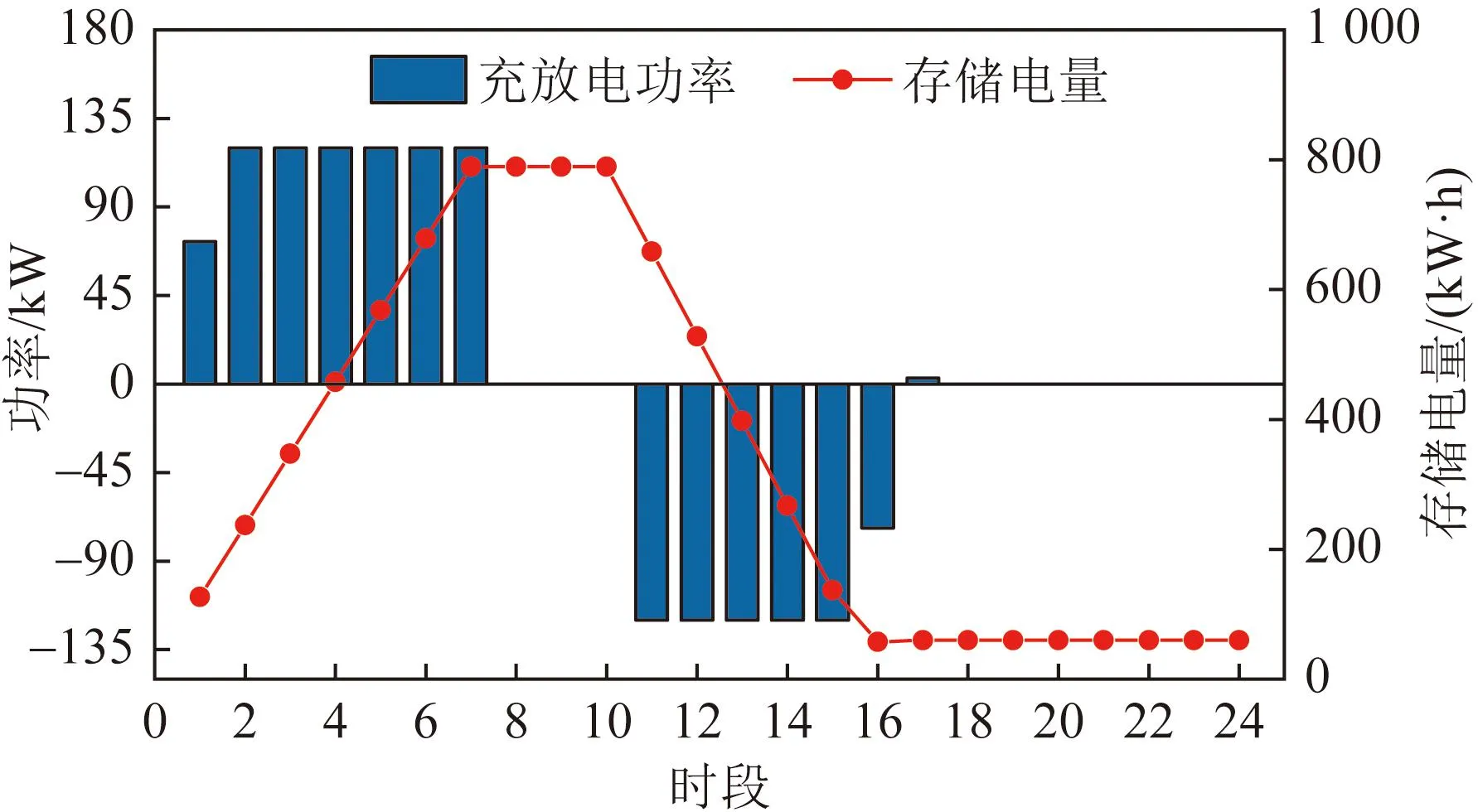
图9 办公楼宇2储能使用情况Fig.9 Energy storage usage of office building 2

综上所述,采用合作联盟的形式进行分布式储能共享,不仅提高了配置储能楼宇储能资源的利用率,还有效减小了未配置储能楼宇自建储能的投资成本,实现了双方的互利共赢。

4.2.2 楼宇集群运行成本分析

楼宇集群运行成本见表2。经计算,经过分布式储能的共享,场景2下楼宇集群运行成本较场景1降低了10.22%。

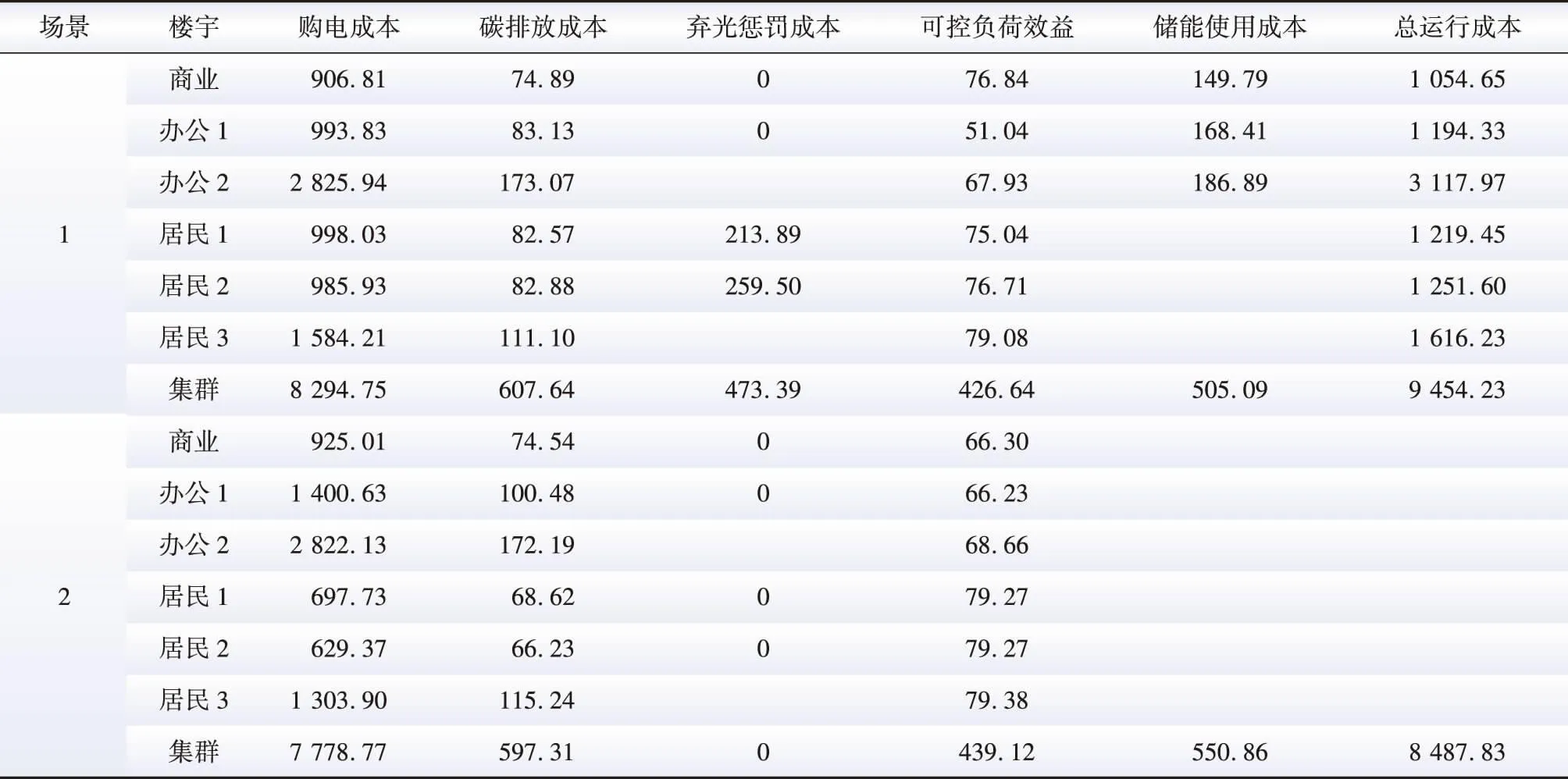
表2 楼宇集群运行成本Table 2 Operating cost of building cluster 元

具体而言,场景2下楼宇集群的购电成本较场景1降低了6.22%。购电成本的降低,既是由于楼宇集群利用储能设备进行电价峰谷价差套利操作所带来的电费节省,亦是由于储能共享提升了楼宇集群运行的灵活性,提高了光伏就地消纳率。光伏就地消纳率的提高不仅降低了楼宇集群对外部能源的依赖性,减少了购电成本和碳排放总成本,还使得楼宇集群弃光惩罚成本降为零元。另外,居民楼宇充分利用共享储能资源的削峰填谷作用提升了SEA的用电满意度,进而提高了楼宇集群的可控负荷效益。

由于储能资源的共享提高了储能设备的利用率和充放电操作频次,使得场景2下楼宇集群的储能使用成本较场景1增加了9.06%,此结果与图5给出的楼宇集群储能使用情况一致。由于集群储能使用成本的增加幅度小于其他三项成本的下降幅度之和,因此以合作联盟形式进行分布式储能资源的共享使用,可有效降低楼宇集群的整体运行成本,即通过储能资源的合作共享可以获得超出储能设备独立运行的合作剩余,体现了合作联盟的整体理性 。

由表2还可看出,办公楼宇1在场景2下的购电成本、碳排放成本较场景1有所提高。这表明办公楼宇1为了降低合作联盟的整体运行成本,以自身利益受损为代价,出让了自配储能设备的部分容量。商业楼宇1的购电成本也体现了这种情况。维持储能合作共享联盟稳定的关键,是通过对合作剩余公平分配而体现对利益牺牲者以合理的成本补偿。

4.2.3 合作剩余分配分析

为分析Raiffa解法及其改进在联盟合作剩余分配中的有效性,在场景2的基础上分别采用两种方法对联盟合作剩余进行分配。

方法1：基于Raiffa解进行合作剩余分配;

方法2：基于改进Raiffa解进行合作剩余分配。

各楼宇在两种方法下的合作剩余分配情况及楼宇运行成本见表3。可以看出,在楼宇集群运行成本降低的前提下,经过两种方法进行合作剩余分配后各楼宇的运行成本均出现不同程度的下降,满足了楼宇参与联盟合作的个体理性要求。

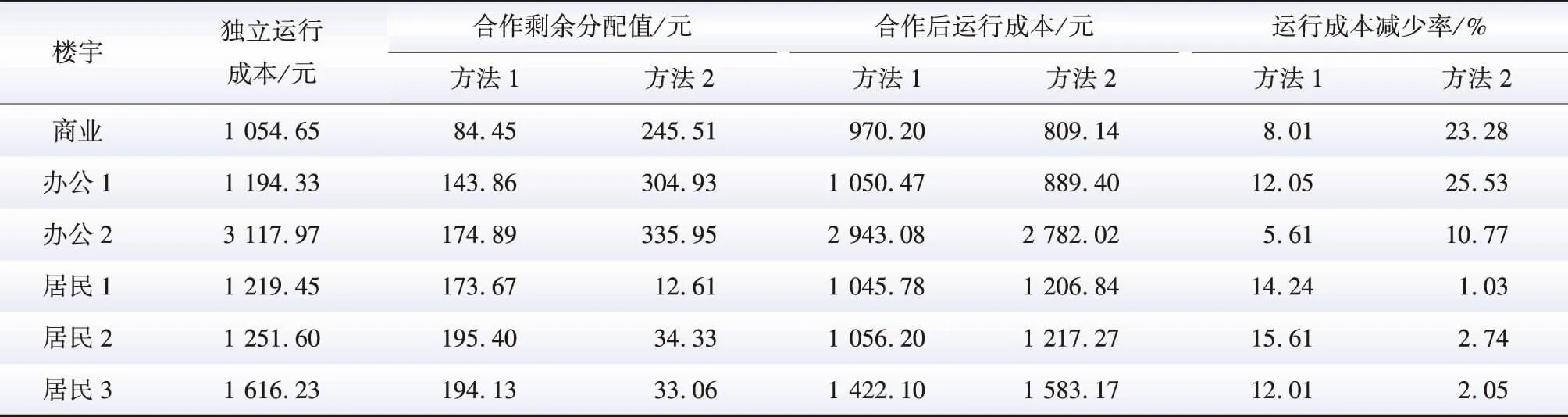
表3 经合作剩余分配后楼宇运行成本Table 3 Operating cost of building after surplus allocation through cooperation

经计算,方法1中,商业楼宇运行成本减少了8.01%。商业楼宇共享自配储能资源参与合作联盟,为了降低合作联盟整体的运行成本,甚至增加了自身的购电成本,但经合作剩余分配后其运行成本减少的幅度远低于未配置储能的居民楼宇,办公楼宇亦是如此。这表明基于Raiffa解法的合作剩余分配因未能体现各楼宇参与联盟时的投入差异,合作剩余分配结果欠合理,不利于储能共享联盟的稳定性。

方法2中,配置储能资源的商业楼宇和办公楼宇1、2经合作剩余分配后其运行成本分别减少了23.28%、25.53%和10.77%,幅度远高于未配置储能的居民楼宇。办公楼宇2因其在自身储能容量不足时段共享使用了商业楼宇、办公楼宇1共享的部分储能容量,所以在经合作剩余分配后,其运行成本下降幅度低于商业楼宇和办公楼宇1。上述结果表明,改进的Raiffa解法通过对合作剩余分配投入权重的调整,体现了储能共享联盟中各楼宇在储能资源投入方面的差异,使得合作剩余的分配更加公平合理,有利于各楼宇参与储能共享的积极性。

但需要指出的是,针对算例中6栋楼宇组成合作联盟的合作剩余分配问题,若采用Shapley值法需要计算(26-1-4)种组合的合作剩余量,而采用Raiffa解法仅需计算(6+1)种组合的合作剩余量,计算量明显减少。

5 结 论

建设储能装置是应对分布式可再生能源出力不可控问题的有效措施,但自建储能设备的投资成本较高且全时段利用率较低。本文以含有部分自建储能装置的城市楼宇集群为研究对象,采用合作博弈理论研究了如何通过储能共享提高储能利用率和降低系统运行成本,并得出以下结论:

1) 储能共享是共享经济思想在储能商业模式中的具体应用。在自有储能共享模式下,楼宇集群中已配置储能楼宇可选择将自身储能资源共享给未配置储能楼宇实现“降本增效”;集群中不易配置储能楼宇可通过储能共享降低设备投入并提高用电灵活性。

2) 储能共享需要适当的合作机制。本文分析了在自有储能共享模式下城市楼宇通过构建合作联盟的形式共享储能资源的机制。算例分析表明,通过合作联盟共享储能提高了储能资源的利用率,减小了楼宇集群的运行成本,体现了合作联盟的整体理性和自有储能共享模式的可行性。

3) 储能共享合作联盟的稳定性有赖于合理的合作剩余分配机制。本文在自有储能共享模式下基于改进Raiffa解法设计了一种考虑储能初始投入差异的联盟合作剩余分配机制。算例分析表明,在楼宇集群整体运行成本降低的前提下,已配置储能楼宇的“降本”幅度远高于未配置储能楼宇,体现了分配方式的公平性,且Raiffa解法的计算量较Shapley值法有明显减少。

附录A

表A1 分时电价Table A1 Time-of-use price

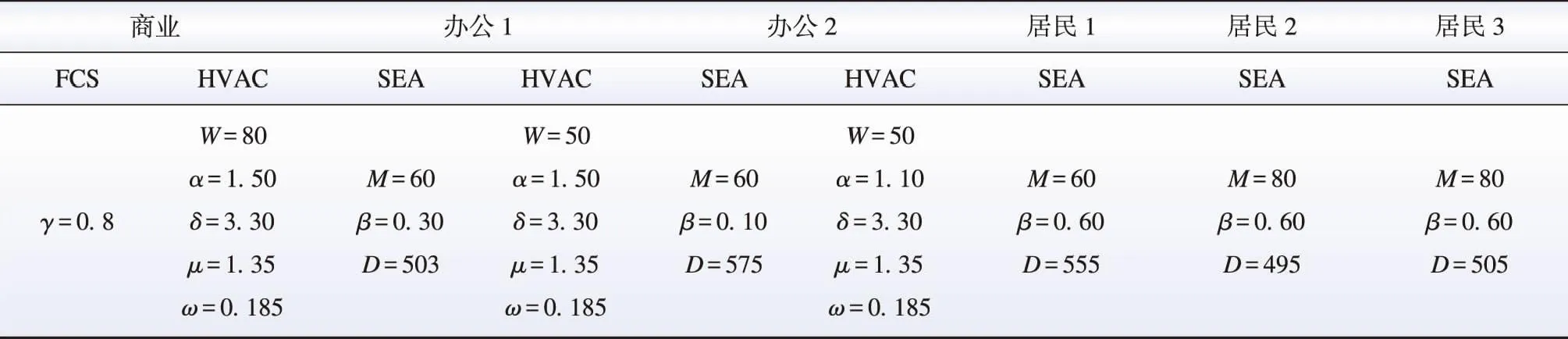
表A2 可控负荷主要参数Table A2 Main parameters of controllable load

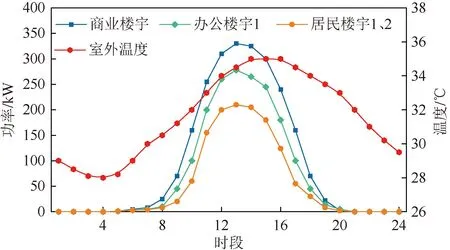
图A2 光伏出力及室外温度曲线Fig.A2 PV and outdoor temperature curve