基于CFD-DEM 的盾构泥浆管道排渣特性参数影响规律研究

刘晓明，李维，黄川，宋孝贺，蔡鸿

（1.广州地铁集团有限公司，广东广州 511430；2.中铁（广州）投资发展有限公司，广东广州 510308；3.中铁隧道集团三处有限公司，广东深圳 512205；4.西南交通大学机械工程学院，四川成都 610031）

0 前言

随着我国隧道建设的规模不断增大，隧道工程开始呈现更为复杂多变的特点，可能会出现一个区间隧道穿越硬岩、上软下硬、断层破碎带及孤石等多种地层的情况［1-2］。针对地层复杂多样的挑战，出现了可以适应多种地层的三模式盾构。三模式盾构是一种具有泥水平衡、土压平衡和TBM 三种掘进模式的掘进机，其适用范围广，可应用于具有多种地质条件的隧道工程［3］。三模式盾构机有泥水循环系统和螺旋输送机两种排渣方式可供选择，三模式盾构机在TBM 模式下掘进时，可采用泥水循环系统进行排渣，该种排渣方式具有刀具寿命长、工作区域无粉尘（省略除尘系统）等优点。但实际施工中对该种工况的泥水循环系统排渣效果和规律不明确，因此对三模式盾构机的排渣特性及参数影响规律进行研究具有重要意义。

目前已有的研究主要有泥浆管道的排渣机制、岩渣在泥浆中的启动流速及运动形态、管道磨耗以及泥浆输送能力计算等方面，并形成一定的研究成果［4-6］。孔玉清［7］以实际盾构工程为背景，针对不同的地层分别进行了泥水循环系统质量守恒计算、泥浆处理效果分析、排渣管携渣能力的计算。YANG 等［8］采用CFD-DEM 方法建立管道排渣仿真模型，通过仿真分析得到泥浆入口速度、岩渣体积分数管道倾斜角度对泥浆压降和管道输送能力的影响规律。WANG等［9］采用CFD-DEM 方法，对某盾构工程泥浆管道系统的非球型岩渣颗粒输送特性进行研究。夏毅敏等［10］采取离散元和流体力学相结合的仿真方法研究了3 种典型形状的石渣在水平管道中的启动流速，得出不同形状石渣的启动流速由小到大为：近球形、扁平状、椭球体。陈健等人［11］以杭州望江路隧道工程为研究背景，建立CFD-DEM 水平排浆管道仿真模型，研究了管道泥浆流速与泥浆密度对管路压力损失及泥浆携渣特性的影响规律。

根据上述研究文献分析，已有部分是利用数值模拟的方法对泥水循环系统的排渣过程进行研究，但是在这些研究中，建立的模型大多是较为简单的水平或倾斜管道，针对组合弯管的内部颗粒运动以及流场特性分析的研究鲜有文献报道；且研究中多采用形状单一的圆球形颗粒，对粒径级配更为复杂或含有复杂形状颗粒的情况需要有进一步的研究［12-13］。

本文作者在理论分析的基础上，基于CFD-DEM建立数值仿真模型对泥浆管道的排渣过程进行模拟，对泥浆系统参数影响规律进行了研究，解决泥水循环系统排渣过程难以可视化、泥浆和卵石颗粒运动特性难以定量分析的问题。研究结论可为盾构排渣的施工控制提供参考。

1 工程背景

1.1 总体概况与地质构造

此次研究的工程背景为广州地铁某隧道施工区间，该区间全长1 086.5 m，隧道埋深19～65 m，采用暗挖法施工。图1 所示为该区间的左线地质剖面图，盾构始发后，首先会穿越全风化花岗岩的软土地层，然后进入大部分为微风化花岗岩的硬岩地层，期间需穿越一个风化凹槽，该部分岩石裂隙发育、岩体破碎造成地下水富集，地层水压较大。

图1 盾构区间地质剖面Fig.1 Geological profile of the interval

1.2 三模式盾构TBM 模式排渣工作原理

三模式盾构在TBM 模式下掘进采用泥水循环系统进行排渣的工作原理如图2 所示。该模式下盾构处于“敞开式” 掘进，盾构的泥水仓保持常压，在下部进浆管的冲刷搅拌下，泥浆和通过刀盘开口进入泥水仓的岩渣搅拌混合，然后通过排浆泵和泥浆管道将泥浆和岩渣输送到隧道外。

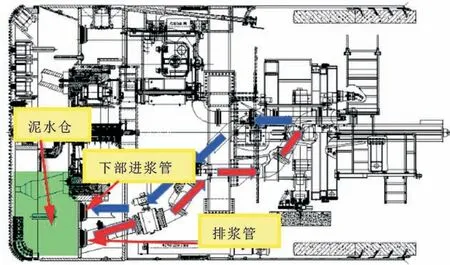
图2 TBM 模式泥水循环系统排渣原理Fig.2 The principle of slurry circulation system slag discharge in TBM mode

利用敞开式TBM 在硬岩地层中进行掘进可以提高掘进效率，但是掘进产生的岩渣颗粒量较大、粒径分布较广，这对泥水循环系统提出了较高的要求。

2 理论模型

2.1 泥浆相

流体连续相遵循Navier-Stokes 方程，不考虑泥浆和岩渣间的热传递与相变特性，在欧拉坐标下分别建立流体相的质量守恒方程和动量守恒方程［12］：

式中：ρf为流体的密度；t为时间；u为流体速度；μ为流体的动力黏度；Fpf为流体所受的颗粒作用力；p为作用在流体微元体上的压力。

2.2 颗粒相

固相颗粒的控制方程为颗粒的动量守恒方程和角动量守恒方程［14］：

式中：mp为颗粒的质量；vp为颗粒速度；g为重力加速度；Fpw为颗粒-壁面相互作用力；Fpp为颗粒-颗粒的相互作用力；Ip为颗粒旋转惯量；ωp为颗粒角速度；Mct为由接触力引起的扭矩；Mfp为流体对颗粒的扭矩；Ffp为流体对颗粒的作用力。

2.3 临界沉淀流速

临界沉淀流速定义为管道内运输的固体颗粒不发生沉淀淤积的最低流速，泥浆设计流速必须高于临界沉淀流速，才不会使管道发生淤堵。经过泥浆处理系统，新鲜泥浆主要包含的是粒径极小的颗粒，在输送过程中不易沉积，因此主要关注排浆管的临界沉淀流速，并以此为依据对泥水循环系统的参数进行设计。临界沉淀流速计算公式可采用Wasp 计算公式：

式中：vL为Wasp 临界沉淀流速，m／s；FL为固体颗粒浓度和粒径的常数，取1.34；d2为排浆管直径，根据盾构开挖直径，取0.25 m；Gs为土体颗粒比重，取2.7；γ为比重，根据工程经验，取1.4；d为颗粒粒径，取0.05 m。计算得到该工况下临界沉淀流速vL＝2.54 m／s。

临界沉淀流速vL为排浆管必须保证的最低流速，实际排浆时使用的流速v2需在此基础上进行设计：

经过计算，得到排浆管的设计流速为3.17 m／s。

2.4 耦合模型验证

为了验证建立的CFD-DEM 耦合模型的准确性和可行性，本文作者利用ZOUAOUI 等［15］建立的管道固液体输送实验装置来进行仿真验证。根据文献中的实验装置和测量装置，利用上文的CFD-DEM 仿真模型模拟部分管道的输送过程，将仿真模型计算得到的压力损失和实验得到的实验值进行对比验证，得到对比结果如图3 所示。分析发现：随着泥浆流速的增加，压力损失实验值和仿真值均成上升趋势，且实验值和仿真值的误差在1.13%～16.85%之间，误差大小在工程可接受的范围内。综上所述，CFD-DEM 耦合仿真方法可模拟管道内流固混合体的运动，可用来模拟泥浆管道排渣过程。

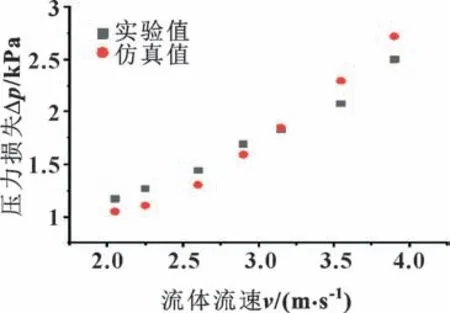
图3 不同流速下液体压力损失仿真值与实验值对比Fig.3 Comparison of simulated and experimental values of liquid pressure loss at different flow rates

3 管道排渣数值仿真模型

3.1 排渣管道三维模型及网格划分

根据实际三模式盾构排浆管道的尺寸大小，同时考虑到计算机的计算能力，建立盾构主机内的排渣管道，以此部分的管道作为研究对象，对泥浆管道排渣过程进行仿真研究。利用三维建模软件建立泥水循环系统在主机部分的排渣管道三维模型，如图4 所示，管道内径为250 mm。

图4 排渣管道三维模型Fig.4 3D model of the slag discharge pipe

研究所涉及的模型尺寸较大，为了提高计算仿真的速度与精度，采用六面体网格对流场进行网格划分。在保证模拟精度的前提下尽可能减少网格的尺寸，以便减少模拟时间。在ANSYS Workbench 的Mesh 模块中进行网格的划分，弯管部分和截面网格划分结果如图5 所示。

图5 弯管（a）及截面（b）网格划分结果Fig.5 Meshing of elbows（a）and sections（b）

3.2 边界条件的确定

（1）流体相边界条件

对于文中所涉及的流体相，入口边界采用速度入口边界条件，泥浆流速取计算得到的排浆管设计流速3.17 m／s。此次研究的排浆管道，采用真空泵进行抽排输送，在出口位置要保证真空度，出口边界设置为压力出口边界条件，压力为-101 000 Pa；流体与壁面的边界条件采用无滑移壁面条件。

泥浆管道内部的泥浆流速较快，管道直径较大，雷诺数Re大于3 200，故泥浆在排浆管道中的流动属于湍流流动。仿真的湍流模型采用标准κ-ε模型，设置泥浆的密度为1 200 kg／m3，黏度为20 mPa·s。

（2）固体相边界条件

三模式盾构的TBM 模式主要用于硬岩地层，通过地质勘查报告，该盾构区间的硬岩地层主要为微风化花岗岩地层，地层岩石参数见表1。

表1 岩石物理参数Tab.1 Petrophysical parameters

参考已有研究文献，TBM 掘进时产生的岩渣形状主要为扁平状，长轴与短轴之比为1.5、长轴与厚度之比为4.5［16］。利用EDEM 软件建立4 种长轴分别为30、50、70、90 mm 的扁平状岩渣颗粒，长轴为50 mm 的岩渣颗粒模型如图6 所示，其他颗粒建立形状和方法与之类似。

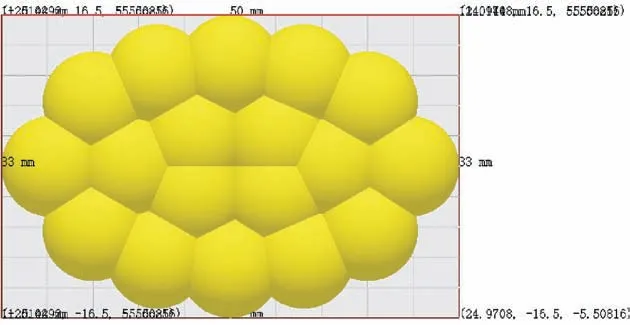
图6 长轴为50 mm 岩渣颗粒模型Fig.6 The slag particles model which long axis is 50 mm

为确定不同尺寸的岩渣颗粒的分布比率，结合实际工程的观测情况，分布比率按Rosin-Rammle 计算，可得到长轴尺寸为30、50、70、90 mm 的岩渣颗粒质量分别按10%、50%、30%和10%的比例进行分布。

盾构掘进进入稳定状态后，单位时间内掘进产生的岩渣量一定，泥水循环系统的排渣能力需与开挖渣土量相匹配。因此，通过在仿真模型管道入口设置岩渣颗粒生成工厂，生成一定质量流量的岩渣颗粒。

可利用下列公式计算开挖渣土量：

式中：Q为开挖渣土量，m3／h；D为隧道开挖截面直径，取6.28 m；vs为盾构推进速度，mm／min。取盾构掘进速度为15 mm／min，则利用公式计算单位时间出渣量Q为27.88 m3／h，即20.91 kg／s。因此颗粒工厂岩渣颗粒生成质量流量设置为20.91 kg／s。

颗粒与颗粒之间、颗粒与管道的接触模型采用Hertz-Mindlin（no slip）模型，该接触模型需要输入的接触参数主要包括：岩渣颗粒与岩渣颗粒及岩渣颗粒与泥浆管道内壁之间的恢复系数、静摩擦因数以及滚动摩擦因数。颗粒与颗粒之间以及颗粒与管道之间的互作用因数如表2 所示。

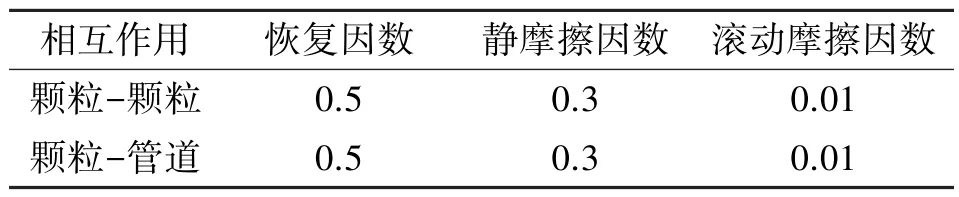
表2 仿真接触参数Tab.2 Simulation contact parameters

3.3 耦合仿真设置

在固液两相流中，其两相间作用力较为复杂，此次研究建立的数值仿真模型只考虑泥浆流体对岩渣颗粒曳力和升力的作用，忽略一些影响很小的其他作用力。目前常用的曳力模型有3 种：Freestream 曳力模型、Ergun and Wen ＆Yu 曳力模型以及Di Felice 曳力模型。这3 种模型都是根据实验得到的经验或半经验模型，文中采用Freestream 曳力模型。岩渣在泥浆管道中的运动仿真需考虑Saffman、Magnus 升力和Fluid-Induced Torque（流体诱导转矩）［17］，文中选择这3 种升力模型对岩渣受到的升力进行计算。

在CFD-DEM 耦合时，两个软件间的时间步长之比应控制在20～100 之间。结合仿真时间和仿真精度，在离散元软件中设定时间步长为1×10-5s，为Rayleigh 时间步长的22.4%，在CFD 软件中设定的时间步长取EDEM 时间步长的50 倍，为5×10-4s，迭代20 000 步，物理时间为10 s。

4 耦合仿真结果分析

4.1 流场特性分析

图7 所示为泥水循环系统输送进入到稳定状态后，管道内部泥浆流场的压力分布云图。可知：管道入口处的压力较高，管道内部的压力随着泥浆运动的方向逐渐降低。在直管部分，泥浆的压降一部分是由于沿程压力损失造成，相当一部分是用来对颗粒进行加速运输造成的。在管道的弯管部分，流体与管壁碰撞，对流体的运动造成了较大的影响，因此在弯管处泥浆的压力分布较为复杂。弯管外侧压力较大，弯管内侧泥浆压力较小。

图7 泥浆管道总体压力分布Fig.7 Overall pressure distribution of mud pipes

图8 所示为泥浆在管道中的整体速度分布云图。可知：在不同的位置有不同的速度变化分布；随着直管的延伸，除管壁附近的泥浆速度由于摩擦作用较小之外，其余部分基本分布均匀；在管道弯管处，由于惯性作用，泥浆与管道内壁碰撞后产生不同程度的湍流，造成靠近弯管内弧处的泥浆流速大于靠近弯管外弧处的泥浆速度，说明弯管的存在会导致泥浆流速的变化，同时也会加大岩渣颗粒的碰撞次数，导致更多的能量损失。

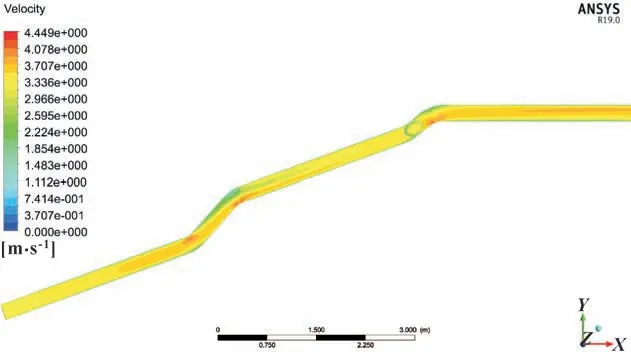
图8 泥浆管道总体流速分布Fig.8 Overall flow rate distribution of mud pipes

4.2 颗粒运动特性分析

图9 所示为泥水循环系统排渣管道输送进入稳定状态后，管道中岩渣颗粒的运动及分布情况。可知：岩渣颗粒进入管道后，大部分情况下，岩渣颗粒沿着管道底部向前输送，这种运动方式与文献［9］中描述的实际工程中大颗粒卵石在盾构排浆管道中的运动方式相同。根据图中岩渣颗粒的速度分布，结合图8 中泥浆的速度分布可发现，岩渣颗粒的运动速度低于泥浆的流速，正是由于该速度差产生的液体拖曳力使得岩渣颗粒在泥浆的作用下向前运动。

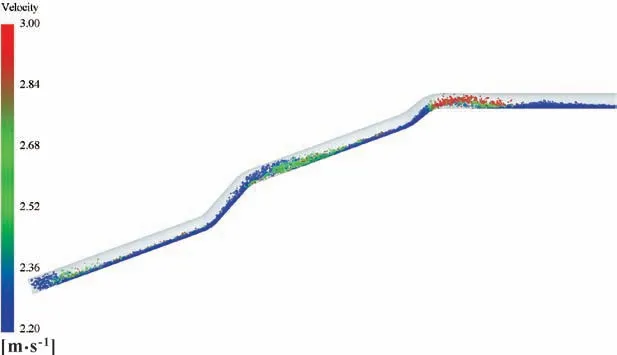
图9 岩渣颗粒运动分布情况Fig.9 Graph of the movement distribution of slag particles

岩渣颗粒由倾斜管道经过弯管进入水平管道，岩渣颗粒在弯管处先是呈“颗粒束” 状运动，然后由于运动惯性，岩渣的轨迹呈现抛物线状向水平管道抛洒，并碰撞到水平管道底部，碰撞使得岩渣速度迅速减小。经过一段距离的运动后，岩渣逐渐在水平管道底部沉积，然后继续向排浆管道的出口方向移动。

图10 所示为管道入口和出口处的质量流量变化。可知：刚开始时管道出口没有岩渣颗粒排出，出口质量流量的值为0，经过一定时间的输送，管道出口开始有岩渣排出，且质量流量值不断增大，在此之后，出口质量流量围绕管道入口处质量流量值浮动，由此可见，该泥水循环系统可实现岩渣的动态稳定运输。

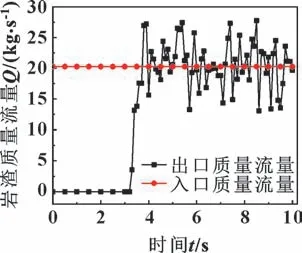
图10 质量流量变化Fig.10 Mass flow change

4.3 排渣特性因素影响规律分析

泥水循环系统输送特性与管道结构参数和操作参数息息相关。通过单因素影响实验方法，可以有效地探究各因素对泥水循环系统排渣特性的影响规律。

（1）泥浆流速影响规律分析

在泥水循环系统的排渣过程中，为了使岩渣能够顺利排出，泥浆必须保证一定的流速。图11 所示为泥浆压力损失Δp随泥浆流速增加的变化规律。可知：泥浆的压力损失会随着泥浆进口速度的增大而二次方增加，泥浆流速由1 m／s 增加到3 m／s 时，管道压力损失增加了6.68 kPa；当泥浆流速由3 m／s 增加到5 m／s 时，泥浆压力损失增加了10.12 kPa；后者增加量为前者的1.51 倍。

当进入管道内的岩渣质量流量一定时，岩渣运动速度越快，越容易被排出管道，因此岩渣的运动速度也是一个重要的考察指标。不同泥浆流速下，岩渣颗粒的平均运动速度变化规律如图12 所示。可以看出：泥浆入口流速为1 m／s 时，岩渣运动速度很低，无法实现岩渣的运输；泥浆流速从1 m／s 增大到2 m／s时，岩渣平均运动速度从0.18 m／s 增加到1.1 m／s，增加了0.92 m／s；泥浆流速从4 m／s 增大到5 m／s时，岩渣平均运动速度从3.07 m／s 增加到4.12 m／s，增加了1.05 m／s。岩渣颗粒的平均运动速度随着泥浆入口流速的增加而增大。因此，泥浆流速越大，越有利于岩渣颗粒的排出，排渣效率越高，但是较大的泥浆流速会带来更大的能量损耗，排浆泵的功率要求更大，施工成本也会增加。

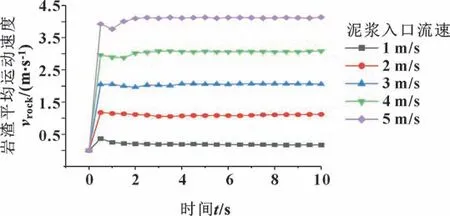
图12 不同泥浆流速下岩渣平均运动速度变化规律Fig.12 Variation of the average movement velocity of slag under different mud flow rates

（2）泥浆密度影响规律分析

泥浆密度ρ是泥浆的重要参数之一，图13 所示为不同泥浆流速下，管道内滞留岩渣的质量随泥浆密度变化的曲线。可知：在流速一定时，管道内滞留的岩渣质量随着泥浆密度的增大而减小，增大泥浆密度使得泥浆的携渣能力增加，岩渣不容易沉积，因此滞留在管道内部的质量减少。泥浆流速不同时，管道内滞留的岩渣质量也不一样，泥浆流速越大，越容易将管道内的岩渣排出，滞留在管道内的岩渣质量减少。

当泥浆密度由1 100 kg／m3增加到1 500 kg／m3，泥浆流速为3 m／s 时，管道内部岩渣滞留质量减少了14.01 kg；泥浆流速为5 m／s 时，管道内部岩渣滞留质量减少了4.11 kg。因此，当流速从低到高变化时，随着泥浆密度的增大，管道内部岩渣滞留质量减小的幅度降低，泥浆密度对岩渣滞留质量的影响减弱。

图14 所示为压力损失Δp随泥浆密度增加而变化的拟合曲线。可知：随着泥浆密度的增加，压力损失的变化呈线性增加的趋势。由图可知，泥浆密度越大，排渣时耗能越大，从而更难输送出去，因此应该根据实际泥水循环系统工作情况，确定合适的泥浆密度参数。

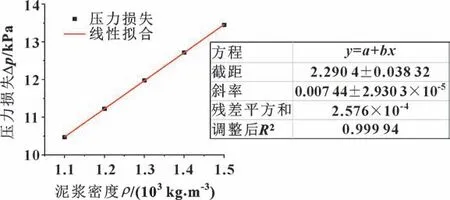
图14 不同泥浆密度下泥浆压力损失拟合Fig.14 Fitting plot of slurry pressure loss at different mud densities

（3）泥浆黏度影响规律分析

合适的泥浆黏度可以使岩渣更容易被运输，但是增加泥浆黏度会使造浆成本增加，也会增加泥浆泵的功率需求。图15 所示为泥浆压降随着泥浆黏度增大而二次方增加：当泥浆黏度由20 mPa·s 增加到60 mPa·s时，泥浆压力损失由11.23 kPa 增加到18.54 kPa，增加了7.31 kPa；泥浆黏度由60 mPa·s 增加到100 mPa·s时，压力损失增加了1.615 kPa。由此可以看出，泥浆黏度对泥水循环系统管道排渣有一定的影响，黏度越大，泥浆的压力损失也就越大，泥浆输送所消耗的能量越大，越难以进行输送。同时，随着泥浆黏度的增大，泥浆黏度对泥浆压力损失的影响在减小。

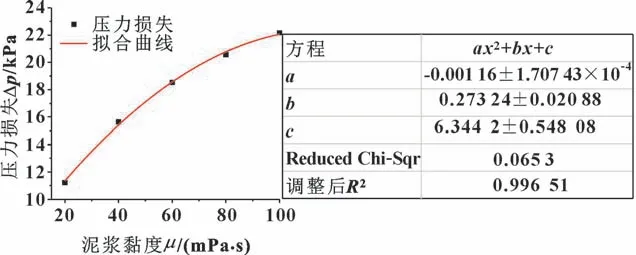
图15 不同泥浆黏度下泥浆压力损失拟合Fig.15 Fitting plot of slurry pressure loss under different mud viscosities

（4）管道直径影响规律分析

管道直径d是泥水循环系统设计时必须考虑的重要参数，明确管道直径的变化对岩渣输送特性的影响规律就显得尤为重要。

图16 所示为泥浆压力损失随管道直径增加而二次方减小：管道直径由150 mm 增加到250 mm 时，压力损失降低了7.51 kPa，管道直径由250 mm 增加到350 mm 时，压力损失增加了2.82 kPa。泥浆压力损失随着管道直径增加而变化的分布符合二次函数拟合规律，由拟合曲线走势可以看出，随着管道直径的增大，泥浆压力损失减小，减小的幅度也在下降。

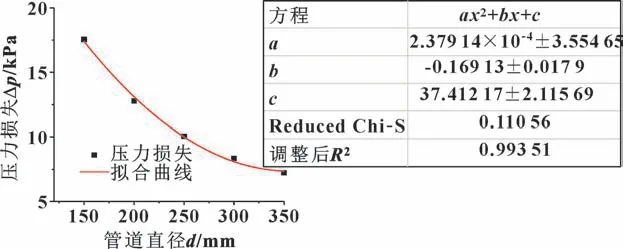
图16 不同管道直径下泥浆压力损失拟合Fig.16 Fitting plot of slurry pressure loss under different pipe diameters

5 结论与讨论

本文作者采用理论分析、CFD-DEM 耦合等方法对三模式盾构在TBM 模式下的泥浆管道排渣特性及参数影响规律进行研究，得到结论如下：

（1）泥浆与管道内壁碰撞后产生不同程度的湍流，造成靠近弯管内弧处的泥浆流速大于靠近弯管外弧处的泥浆速度；岩渣颗粒在管道中的运动形态大部分为在管道底部做推移运动，岩渣经过弯管部分时，会对弯管的外侧造成冲击。

（2）随着泥浆流速、泥浆黏度的增加与管道直径的减小，泥浆管道压力损失二次方增加，带来更大的能量损耗，对排浆泵的功率要求更高。

（3）增大泥浆密度会增加泥浆的输送阻力，导致泥浆管道压力损失线性增加。增大管道直径会减少管道压力损失，降低泥水管道的能量损失。