改进麻雀搜索算法优化BP神经网络的短时交通流预测
王 珅,李昕光,詹 郡,吕 桐
(青岛理工大学 机械与汽车工程学院,青岛 266525)
在城市不可能无限增加车道的情况下,交通控制和交通诱导成为缓解交通拥堵的最好方法。良好的交通控制和交通诱导需要精准的短时交通流预测作为支撑[1]。由于交通流的不确定性和突发性,传统的线性模型不能对交通流进行很好地预测。BP神经网络通过其较强的输入到输出的映射功能、自学习和自适应能力,可以对具有非线性变化的交通流进行很好地预测。但传统BP神经网络的预测结果对初始参数的选取具有极高的依赖性,不当的初始参数选取会导致程序陷入局部最优或收敛过慢[2-4]。
近年来,各种群智能优化算法凭借搜索能力强、收敛速度快、结果不依赖初始参数选取等特点,在神经网络的优化上得到广泛应用。例如通过粒子群算法来优化BP神经网络模型,从而提高BP神经网络短时交通流预测模型的预测精度[5-7]。但粒子群算法收敛速度慢,寻优能力较弱。2020年提出的麻雀搜索算法(Sparrow Search Algorithm,SSA)相较于粒子群算法,具有参数少,结构简单,收敛快等特点,获得了较广泛应用。李雅丽等[8]针对最近几年来较为典型的几个群智能算法,利用22个测试函数,从算法的精度、收敛速度和预测结果的稳定性等方面对算法进行了对比,对比结果显示麻雀搜索算法的性能远超其他算法;刘丽娜等[9]用改进麻雀搜索算法来求解作业车间调度问题,获得了更好的最小值、平均值和寻优成功率;ZHANG等[10]用改进麻雀搜索算法设计了移动机器人的仿生路径规划;JIANG等[11]利用改进麻雀搜索算法来解决现有算法求解飞行器轨迹优化问题时收敛精度低、易陷入局部优化的问题。
本文提出一种基于改进麻雀搜索算法(Improving Sparrow Search Algorithm,ISSA)优化BP神经网络的短时交通流预测模型(ISSA-BP),针对标准麻雀搜索算法易收敛于原点的问题,对标准麻雀搜索算法中发现者和加入者的位置更新公式进行部分改进,改善标准麻雀搜索算法的全局探索能力,降低计算复杂度。利用改进麻雀搜索算法优化BP神经网络的权值,使BP神经网络预测模型的收敛速度更快,精度更高。
1 改进麻雀搜索算法
麻雀搜索算法和粒子群算法都是根据鸟类的种群觅食行为提出的。2020年提出的新型的麻雀搜索算法不仅考虑到了鸟类的觅食行为,还考虑到了针对捕食者的反捕食和种群中鸟类之间的夺食行为[12],同其他智能群体优化算法相比较,麻雀搜索算法的初始参数更少,收敛速度更快[13]。
1.1 标准麻雀搜索算法
在SSA中,假设有N只麻雀在D维搜索空间中觅食,则将第i只麻雀在搜索空间中的位置坐标设置为Xi=[xi1,xi2,…,xid],xid表示第i只麻雀在d维度中位置的。D维空间中每一只麻雀的位置都是目标函数的一个解,将麻雀在空间中的位置代入目标函数会得到解的值,按照解的大小对麻雀种群进行排序,排序靠前的麻雀作为发现者,将优先获取食物,并为加入者提供觅食方向。发现者的位置更新公式为
(1)
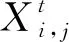
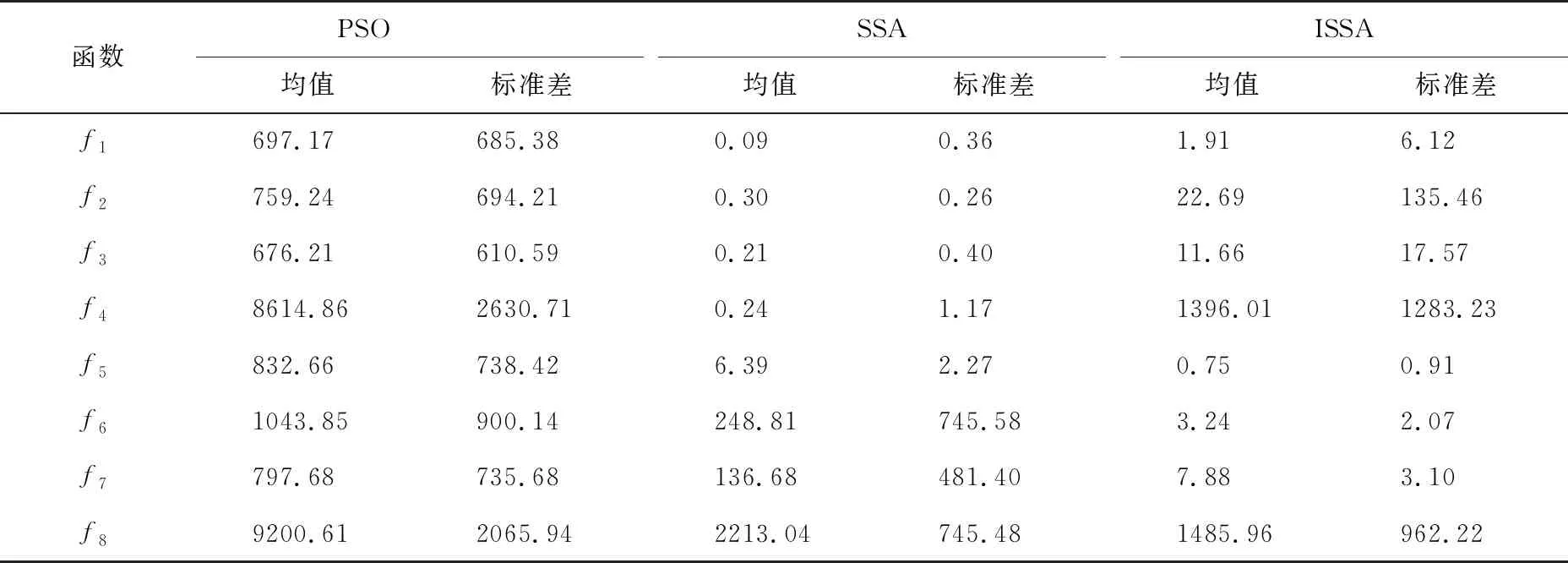
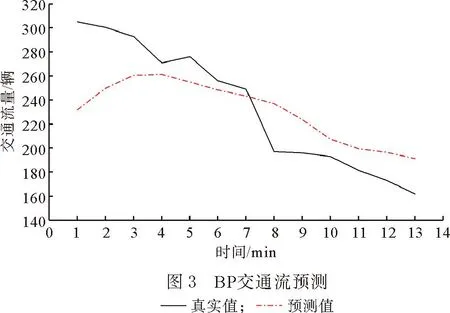
在式(1)中,当R2 (2) 在麻雀种群中约有10%~20%的麻雀负责警戒,这些麻雀会根据自己的判断来确定是否有危险,这部分警戒麻雀的位置更新公式为 (3) 在式(3)中,当fi>fg时,表示该麻雀不在种群中心,需要往中心靠拢;当fi=fg时,表示种群中心的麻雀需要向其他麻雀靠拢。 图1 迭代散点分布 利用3个测试函数对原算法的缺陷进行验证。对带入3个测试函数的原算法选择相同的参数:维度为2、麻雀数为10、循环次数为100、测试次数为50。具体测试函数和测试结果的平均值如表1所示。 表1 测试函数参数和测试结果 由表1可知,随着最优值的位置距离原点越远,测试结果的平均值越大,因此标准的SSA算法对于最优解越靠近原点的函数,寻优的效果越好。但BP神经网络的最优值所对应的权值和阈值未必靠近原点,所以需要对标准SSA算法进行改进。 保留标准麻雀搜索算法的收敛和反捕食公式不变,对易收敛于原点的位置更新公式进行部分改进。受粒子群算法[14-15]中粒子会根据最优粒子的位置和自身最优位置进行搜索这一行为的启发,将位置更新公式分别改为以自身为中心的搜索模式和以全局最优位置为中心的搜索模式,在增加搜索多样性的同时避免麻雀在探索过程中向原点收敛,同时也降低了计算的复杂度,提高程序的运行效率。因此,改进式(1)中当R2 (4) (5) 式中:L为搜索空间的长度;r为随机数,取值范围为[-1,1];Pm为常数,表示发现者的数量;a为搜索因子。 a的值从0.2非线性缩减至约0.03,其计算公式为 a=0.2-0.1×[exp(t/Tm)-1] (6) 式(6)中利用以自然数为底数的指数函数在[0,1]的取值范围内的函数值先缓慢增加后快速增加的特点,令搜索因子a在迭代初期能以较大的值缓慢缩小,提高发现者在自身附近的搜索范围;迭代后期搜索因子a的值以较快的速度缩小为较小值,提高自身的收敛速度。 以式(4)中的粒子搜索范围构建f(x)=a×L×r×(x/Pm)函数并将结果制作为散点图,其中,a=0.2,L=200,Pm=30。表示为迭代初期按适应度值排序的麻雀个体的搜索范围。将所构建函数的计算结果制作为散点图,散点分布图如图2所示。 图2 麻雀散点分布 从图2中可以看出种群中的麻雀个体随着适应度的逐渐降低搜索范围会逐渐变大。迭代后期的散点由于a的缩小更加收敛,变化幅度将会更小。使得麻雀种群前期有较大的搜索空间,后期有较快的收敛速度。 为了使算法在迭代前期具有较高的全局搜索范围,迭代后期具有较快的局部收敛速度,令跟随发现者觅食与不跟随发现者觅食的加入者的比例系数随迭代次数指数衰减,计算公式为 H=b+b·ct (7) 式中:H为加入者中不随发现者觅食的比例系数;b为常数,取值为0.35;ct为衰减因子,根据最大迭代次数和所需衰减到的大小进行设置,取值为0.999。 为测试改进麻雀搜索算法的性能,选取4个国际通用的基准测试函数(f1~f4)[16]对ISSA进行仿真测试,同时对这4个测试函数的最优值位置进行偏移从而衍生出(f5~f8)4个偏移函数,其中f1,f5仅有1个极值,其余函数均有多个极值。8个测试函数的参数值如表2所示。 表2 8个测试函数的参数值 利用上述8个测试函数对ISSA,SSA和PSO进行测试,为保证算法的公平性及准确性,给3种算法设置相同的参数。种群中的个体数均为30,搜索空间的维度均为30,最大迭代次数均为1000,每个函数独立运行50次,分别记录每次测试的最优值位置与实际最优值位置之间距离的标准差,计算公式为 (8) 计算3种算法在8种测试函数中的最优值位置与实际最优值之间距离的平均值和标准差,用以比较算法的搜索精度和稳定性。PSO,SSA,ISSA算法对8个测试函数的测试结果(小数点后保留2位有效数字)如表3所示。 表3 不同模型对于8个测试函数的误差 由表3可知,SSA和ISSA在8个函数上的寻优效果均好于PSO算法;SSA算法在f1~f4函数(函数最优解在每个维度上均为0)寻优好于ISSA,这是由于SSA算法会收敛于原点;在f5~f8函数(函数最优解在每个维度上的值均为50)上ISSA寻优效果好于SSA,并且ISSA在(f1,f5)、(f2,f6)、(f3,f7)、(f4,f8)这4组对比函数上寻优效果接近,而SSA在这4组对比函数上的寻优效果相差很大,所以ISSA相比较于SSA算法有着更好的普遍适应性,更适合用于解决实际问题。 针对BP神经网络在非线性预测中的优缺点,用改进麻雀搜索算法的最优解作为BP神经网络的初始权值,结合交通流特性构建基于改进麻雀搜索算法优化BP神经网络(ISSA-BP)的短时交通流预测模型。 1) 利用python语言和Tensorflow深度学习框架设计神经网络层数,确定输入层、隐藏层以及输出层的节点个数和每层的激活函数,搭建BP神经网络模型。 2) 搭建改进麻雀搜索算法模型,确定麻雀种群的适度值函数。用第1)步中构建的BP神经网络期望值与预测值之差的绝对值之和作为麻雀的适度值函数来构建ISSA算法模型。 3) 通过迭代来寻找到最优适度值。输出其所对应的位置作为最优解,将输出的最优解作为BP神经网络的权值和阈值。将BP神经网络代入训练集进行训练,当训练精度达到要求或达到最大迭代次数后,输入测试集,并输出最终测试结果与真实值之间的误差。 为了对短时交通流预测模型的精度进行判定,采用平均绝对百分误差(MAPE)、平均绝对值误差(MAE)和均方误差(MSE)进行误差分析[17-19],公式如下: (9) (10) (11) 式中:EMAPE,EMAE,EMSE分别为平均绝对百分误差值、平均绝对值误差值、均方误差值。 模型的输入为3,输出为1。BP神经网络以及PSO-BP,SSA-BP,ISSA-BP模型的BP神经网络部分采用相同的网络结构,模型的输入层输入节点个数为3;隐藏层为2层,每层的节点个数均为10;输出层的节点个数为1;激活函数采用Sigmoid函数。 为了评价ISSA-BP模型的性能,采用西安市区某道路断面18 d交通流量数据[20]进行实验测试。该道路断面的交通流量数据以15 min为间隔,从7:30开始到11:30截止,每天16组数据,共288组数据。首先对数据进行预处理,删除数据集中的异常值并利用牛顿插值公式进行填充。数据集中的交通流数据只有每天的16个数据为连续数据,每天16个交通流数据除去作为特征输入的3个数据,每天可制作13组训练数据。为了使模型达到充分训练,将前17 d的数据制作为训练集,共221组训练数据;最后一天的数据制作为测试集,共13组测试数据。将训练集和测试集数据分别输入BP,PSO-BP,SSA-BP,ISSA-BP神经网络模型进行短时交通流的预测,比较各个模型的预测输出。4种短时交通流预测模型的真实值曲线和预测值曲线如图3-图6所示。 从图3-图6中可以看出,ISSA-BP模型相较于其他3个模型的预测值曲线更贴合真实值曲线。基于BP和SSA-BP的短时交通流预测结果前半部分小于真实值,后半部分大于真实值,二者的预测结果均不能很好地表现出交通流的变化趋势;基于PSO-BP和ISSA-BP的短时交通流预测结果在真实值上下波动,二者的预测结果均能较好地表现出交通流的变化趋势,但基于PSO-BP的预测值曲线与真实值曲线之间的差值波动较大,预测的交通流量与真实值之间的误差较大;基于ISSA-BP模型的预测值曲线相较于PSO-BP的预测值曲线更贴合真实值曲线,能够更好地满足交通流变化的预测。 为更科学直观地判断4种交通流预测模型的预测效果,利用3.2部分所选择的3种误差评价指标对4种模型的交通流量预测结果进行对比分析,对比结果如表4所示。由表4可知,基于ISSA-BP的短时交通流预测模型相较于其他3个预测模型,其预测结果在3种误差分析中均表现最好。从MAPE评价指标的对比结果来看,ISSA-BP模型的预测精度比BP模型高49.17%,比PSO-BP模型高38.47%,比SSA-BP神经网络模型高40.64%;从MAE评价指标的对比结果来看,ISSA-BP模型的预测精度比BP模型高48.85%,比PSO-BP模型高38.71%,比SSA-BP神经网络模型高40.99%;从MSE评价指标的对比结果来看,ISSA-BP模型的预测精度比BP模型高68.34%,比PSO-BP模型高61.84%,比SSA-BP神经网络模型高63.36%。说明ISSA-BP在短时交通流预测方面具有更好的预测精度。 表4 4种预测模型的误差 针对标准麻雀搜索算法易收敛于原点和局部最优值的缺陷,对麻雀群体中的发现者和部分加入者的位置更新公式进行改进,使其不再轻易收敛于原点,并增强麻雀种群前期的全局搜索能力使其不易陷入局部最优。应用4个国际通用的基准测试函数和4个偏移测试函数对ISSA的性能进行了验证,结果显示ISSA在8个测试函数上的表现均优于PSO,在最优值不在原点的偏移测试函数上的表现优于SSA。ISSA比PSO的测试表现更好,比SSA拥有更好的普遍适应性。用改进的麻雀搜索算法得到的最优解作为BP神经网络的初始权值,构建了ISSA-BP短时交通流预测模型。通过实验测试对SSA模型、PSO模型和BP神经网络模型进行了对比分析,结果显示ISSA-BP模型的误差最小,预测精度最高。下一步考虑应用该算法对多种因素以及特殊因素影响下的短时交通流量进行预测。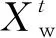
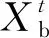
1.2 麻雀搜索算法的缺陷
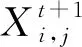
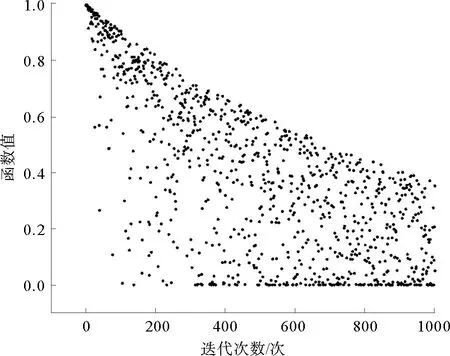

1.3 麻雀搜索算法的改进
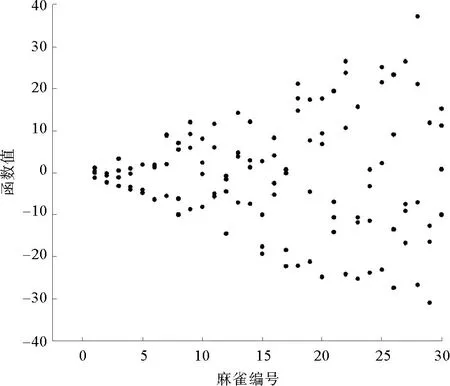
2 改进算法的测试
2.1 测试函数

2.2 算法测试
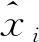
3 短时交通流模型构建与实验测试
3.1 构建模型
3.2 模型评价
3.3 实验测试

4 结论

