大力值电磁作动器电磁热耦合分析与性能优化
马欣源,武倩倩,2,刘碧龙,*
(1.青岛理工大学 机械与汽车工程学院, 青岛 266525;2.工业流体节能与污染控制教育部重点实验室, 青岛 266525)
船舶等大型机械的动力系统在运行时产生的振动对机械本身有很多不利影响[1],长期的振动会导致部分零件出现疲劳、发热等现象,影响其工作精度和性能,采用减振装置能有效降低振动带来的负面影响。电磁作动器作为一种主动控制的减振装置,因其快速响应、输出力可控性好等一系列优点[2],满足柴油机轴系的横向振动控制需求。瑞典[3]、澳大利亚[4]等国家已经将电磁作动器应用于舰船的主动隔振,并取得了较好的效果。
电磁作动器通过载流导体在磁场中产生的安培力[5]作为减振力。减振力的大小是衡量电磁作动器的重要指标之一[6]。永磁体的磁性随着时间的推移逐渐减少[7],而温度的升高会加快这种退磁现象[8-9],永磁体的退磁现象严重影响安培力的大小。当线圈作为载流导体,并通入交变电流时,线圈内部的导体表面会产生涡流效应[10],使得作动器内部温度升高[11],加快永磁体的退磁。另外,温度升高还会使作动器内部结构形变,对整个系统的减振效果产生影响[12]。
刘军等[13]设计的电磁作动器仅做了动力学分析。昌耀鹏[14]对电磁作动器的磁路、悬挂系统进行了仿真,尚未研究电磁作动器的温度场。马龙华等[15]设计了大功率大力值的双线圈电磁作动器,但由于工作时通入的电流大,导致铜损较高,在自然散热的情况下整个作动器无法长期工作。因此,为提高电磁作动器的综合性能,设计时需要将作动器的稳态温度也作为一项重要设计指标。宋金明[16]设计了一小力值电磁作动器,仿真发现作动器持续工作时线圈产生的欧姆损耗较高,稳态时永磁体的温度大于其额定工作温度。
为了减小电磁作动器自身温度升高对内部结构的影响,创新设计一款大力值低功耗电磁作动器。通过数值分析和有限元模拟的方法对电磁作动器的欧姆损耗等参数进行计算,分析电磁热耦合作用下作动器稳态温度场分布情况。
1 电磁作动器的数学模型
1.1 电磁力的数学模型
电磁作动器是一种将洛伦兹力作为减振力的主动减振装置,永磁体跟导磁体组合成磁路在气隙处产生磁场,通电线圈在磁场中受到洛伦兹力的作用:
F=BIL
(1)
式中:I为线圈通入的电流;B为磁感应强度;L为实际切割磁感线的导线长度。
1.2 电磁作动器的欧姆损耗数学模型
作动器工作时,给激励线圈通入交流电,动子(磁路)和线圈产生与电流频率相同的洛伦兹力,通过悬挂系统使线圈连接外壳向外输出减振力。交流电会使线圈以及线圈内部的导体产生的欧姆损耗大幅度增加。电磁作动器的欧姆损耗一般包括线圈的铜损和磁路中的涡流损耗,铜损是指线圈自身电阻通入电流产生的热功耗;涡流损耗是指在交变电流的工作环境下,线圈内部导体出现感应涡流[17],涡流在导体内流动时,会产生涡流损耗从而引起导体发热[18],在作动器工作过程中产生涡流损耗是导致整体的温度升高的主要原因。
能量输入来自通电线圈,输入功率为
P=UI=PΩ+Pe
(2)
式中:U为电源提供的电压;PΩ为铜损;Pe为涡流损耗。
设线圈的电阻为R,则线圈的铜损为
PΩ=I2R
(3)
(4)
式中:ρ为线圈漆包线导体的电阻率;S0为漆包线导体的截面积。
根据麦克斯韦方程组得知,通入交变电流的线圈会使内部导体产生涡流效应,在铁磁材料表面一定深度产生电流,也就是集肤效应。集肤深度的计算公式为
(5)
式中:f为频率;μ为材料的磁导率;γ为材料的电导率。
根据交流电中的法拉第电磁感应定律得最大感应电动势为
Em=N0BmSω
(6)
则有效感应电动势为
(7)
式中:ω为线圈在磁场中的速度;Bm为线圈通入电流时产生的最大磁通密度;N0为线圈径向排列层数;S为磁场的最大正对面积。
计算功率使用公式:
(8)
由于集肤效应只在表面深度d的厚度存在电流,通过对公式(4)(5)(7)(8)整理得
(9)
式中:h为线圈高度;r为磁路内圈半径。
由式(9)可以看出,频率越高,集肤效应越明显。
线圈内部磁场公式:
(10)
式中:μ0为空气的磁导率;N为线圈的总匝数;r0为线圈的平均半径。
将式(10)代入到式(9)中得
(11)
将式(1)代入到式(11)可得
(12)
1.3 温度场的数学模型
线圈和磁路内部的热量传递主要为热传导方式,热量从介质的高温区流向低温区。由导热基本规律得知,单位时间内通过给定面积的热流量为
(13)
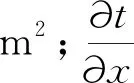
当温度传递到作动器的外壳表面,固体与空气的换热方式为辐射换热。任何高于绝对零度的物体,均以一定波长向外辐射能量,同时也接受外界向它辐射的能量。热辐射不需要任何介质,可在空中传递能量,且能量可进行转换,即热能转换为辐射能或辐射能转换成热能。
物体间的热辐射是相互的,如果它们存在温度差,就会进行辐射换热过程。两物体表面之间的辐射换热计算表达式为
(14)
式中:q为对流换热量;δ0为斯蒂芬-玻耳兹曼常数,δ0=5.67·10-8W/(m2·K4);A为物体辐射换热的表面积;εxt为系统发射率;F12是表面1到表面2的角系数;T1,T2分别为表面1、表面2的绝对温度。
2 大力值双线圈电磁作动器的结构设计与优化
电磁作动器主要由磁路、悬挂系统、线圈、外壳等部分组成。通过式(12)可知,线圈的匝数、高度、平均半径、气隙处的磁感应强度均会影响欧姆损耗。提出一种双线圈电磁作动器,通过减小单个线圈的高度和匝数、增大气隙处的磁感应强度和线圈的平均半径等方法减小磁路的涡流损耗,降低整体的温度。
2.1 磁路结构设计
磁路设计是电磁作动器结构的核心,提出如图1所示的4种双线圈磁路构型方案。
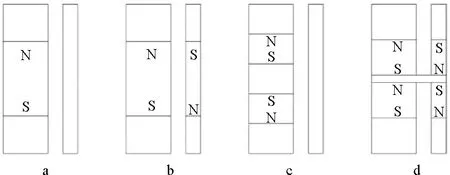
图1 磁路的构型
采用Maxwell 2D对各方案的磁场分布进行仿真计算,仿真结果如图2所示。
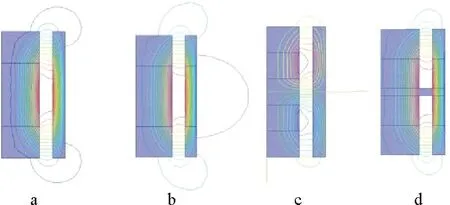
图2 磁路的磁场仿真
选取相同长度的气隙,对中心磁感应强度进行仿真计算,如图3所示。
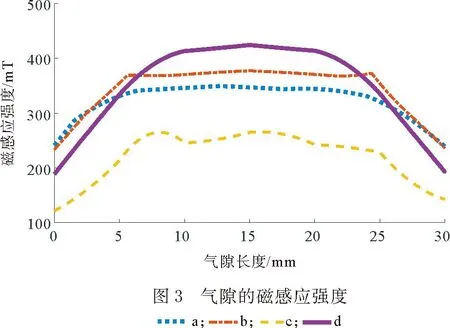
对比图2和图3的4种构型方案可知:a磁感应强度较低;b漏磁严重;c磁感应强度太低;d装配性较好,磁场在6~24 mm区间的气隙范围内分布均匀,磁感应强度高,磁铁也便于装配。最终选择d作为最终磁场构型。
2.2 作动器整体结构设计
根据磁路的结构设计电磁作动器的线圈结构。线圈骨架需要承载线圈通电时产生的洛伦兹力,因此线圈骨架的设计和刚度要求较高。
动子(磁路)通过特殊的板簧悬置于壳体内,形成单自由度振动系统。外壳与线圈骨架刚性连接,当线圈中通入交变电流,电磁作用对动子产生激振力,使之强迫振动[18]。作动器的外壳与减振目标连接后,线圈通入一定频率的交流电,外壳会输出相同频率的减振力。总装配图如图4所示。
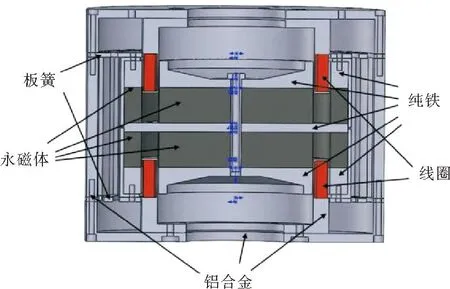
图4 双线圈电磁作动器剖面
3 作动器电-磁-热耦合仿真
电磁作动器内部温度的升高不仅影响线圈的电阻,还会加快永磁体的失磁现象。利用Maxwell 3D仿真欧姆损耗,将结果通过Workbench平台耦合到Icepak温度场中,对电磁作动器进行热仿真,并对比双线圈作动器与文献[19]中同力值作动器的性能。
3.1 电磁作动器损耗的仿真计算
对文献[19]中设计的输出力值为200 N的电磁作动器进行三维建模(图5)。
将文献[19]中的电磁作动器和双线圈电磁作动器的三维模型图导入到Maxwell 3D中进行涡流场功耗的仿真,磁铁材料采用N48SH,外壳和线圈骨架的材料为铝,板簧材料为65Mn。将所有部件赋予材料后,将线圈通入电流,计算20~200 Hz的损耗功率,得出的结果如图6所示。
由图6可以看出,2个作动器的铜损相差不多,双线圈电磁作动器的涡流损耗较低。
3.2 双线圈电磁作动器的热仿真
通过图6可知,当通电频率超过90 Hz,2种作动器的涡流损耗都超过铜损。对双线圈电磁作动器模型在Maxwell 3D中通电频率设为90 Hz,将仿真结果耦合进Icepak中进行热仿真计算,Maxwell 3D中的计算结果如表1所示。

表1 双线圈电磁作动器90 Hz损耗计算 W
各部件材料属性如表2所示,将其添加到Icepak材料库中。
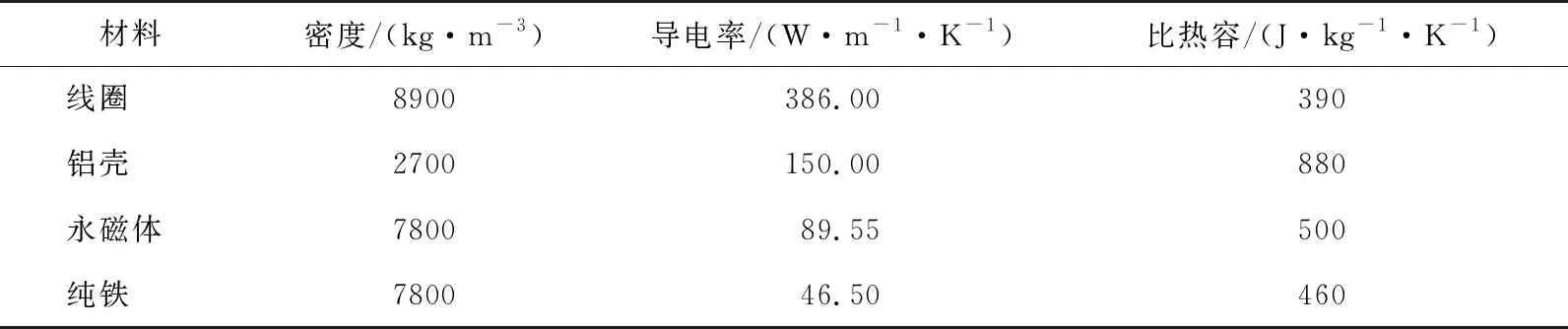
表2 各部件温度场材料属性
3.3 温度场仿真求解计算
在Icepak中的环境温度设置为25 ℃,迭代步数设置为2000,采用非连续性网格划分,如图7所示。求解计算迭代收敛后没有中途报错,说明计算完成。对其进行体处理(Object face),如图8所示,最高温度53.5 ℃,壳体温度48.4 ℃,满足永磁体工作时的要求。
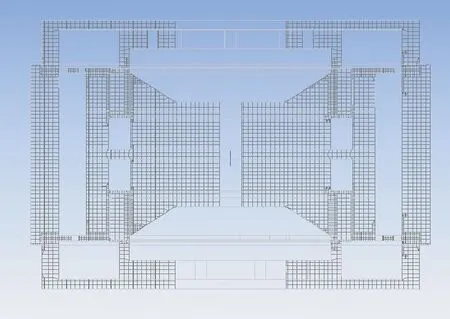
图7 温度场网格剖分
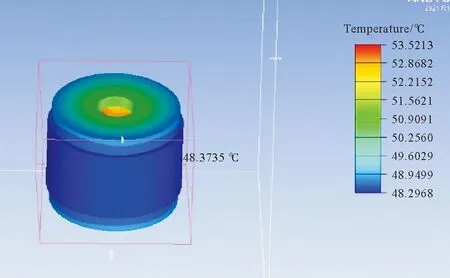
图8 温度场云图
对其进行切面处理(Plane cut)。选出合适的切面,选择所有体,因为作动器是轴对称的,因此所有体在这个切面上的温度分布就是整体的温度分布,如图9所示。
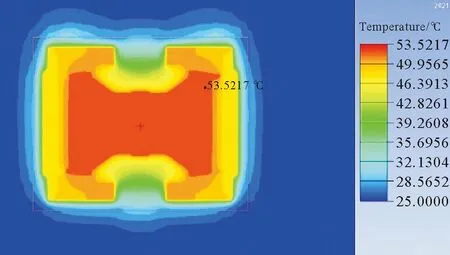
图9 温度场的切片温度
内部的磁路跟线圈的温度基本在53.5 ℃左右,通过自然对流散热,散热的部位主要在外壳跟两端的磁轭部分,且外壳部分温度下降速度较快。
对文献[19]中的作动器进行电-磁-热耦合仿真计算,温度场仿真结果如图10、图11所示,壳体温度64.7 ℃,内部最高温度78.6 ℃。
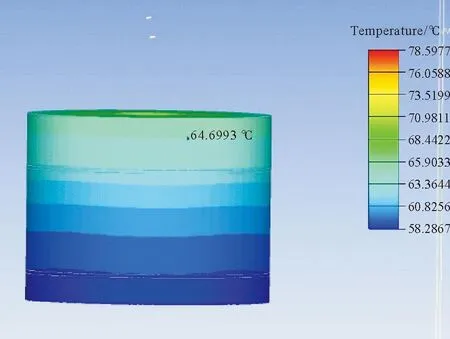
图10 文献[19]电磁作动器温度分布云图
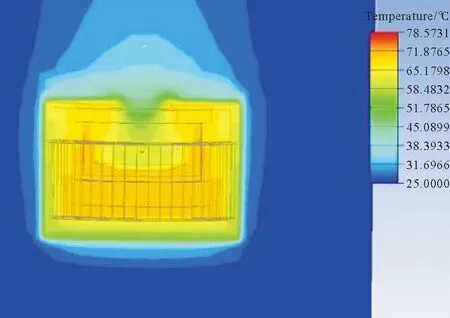
图11 文献[19]电磁作动器温度分布切面
将2种作动器的欧姆损耗及温度进行对比,如表3所示。
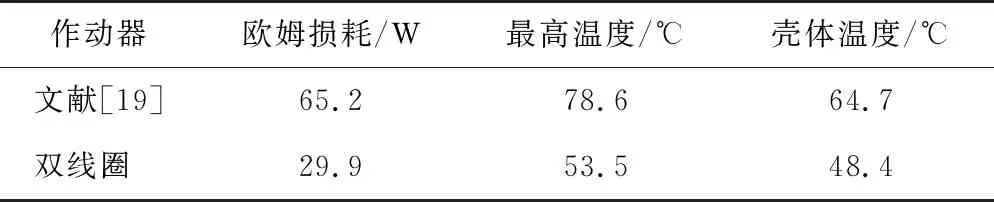
表3 2种电磁作动器温度场对比
结果表明,本文设计的大力值作动器性能更优。
4 结论
本文创新设计了一种双线圈电磁作动器,推算了作动器涡流损耗的计算公式,并以此来设计电磁作动器的参数。通过对作动器电磁场与温度场的仿真计算,得出以下结论:
1) 新型的双线圈电磁作动器与文献[19]中同力值电磁作动器相比,涡流损耗低,双线圈电磁作动器在磁路中的发热功率较低。在温度场的仿真中可以看出双线圈作动器内部温度较低,对永磁体退磁的影响远小于文献[19]的作动器。
2) 在温度场的切面处理中可以看出,双线圈电磁作动器的磁路部分与空气的接触面积较多,且传递到外壳的热较少,使得外壳的温度降低,而且内部磁路的散热也相对加快了。
3) 从仿真结果可以看出,双线圈作动器总功率小且温度在理想范围内,作动器内部永磁体的寿命更长,运行更加可靠。

