基于CS算法优化的SVM短时交通流预测模型
兰添贺,曲大义,陈 昆,刘浩敏
(青岛理工大学 机械与汽车工程学院,青岛 266525)
城市道路交通具有路网复杂,交通流量大和潮汐性明显等特点[1]。随着汽车保有量的增加,交通拥堵的情况日益频发,显著影响了城市居民的出行。因此采用先进的技术手段,对城市路段的车流量进行监测和预测,成为智能交通领域的研究热点之一[2]。短时交通流预测可以为交通管理控制和出行选择提供帮助。近年来,国内外学者对短时交通流预测进行了大量的研究,提出多种方法提高交通流预测的准确度。
目前交通流预测的方法主要分为两类[3],一种是基于传统数理统计模型和回归分析模型的预测方法[4-5],另一种是基于机器学习算法及其优化改进模型的预测方法[6-7]。其中传统数理统计回归分析方法主要有历史平均法模型(Historical Average Method, HAM)[8]、线性回归模型(Linear Regression, LR)[9]、卡尔曼滤波模型[10]和指数平滑模型[11]等。但是交通流量往往具有随机性强和数据量巨大的特点,传统方法很难达到理想的预测效果,因此基于机器学习算法的预测模型成为交通流预测研究的热门方向。机器学习算法具有收敛速度快和适应力强的特点,能够大大提升交通流预测的准确度[12]。VLADIMIR等[13]提出一种能够实时进行短时交通流预测的模型,该模型采用随机森林算法(Random Forests, RF)。RF算法参数少,训练速度快。通过实际数据证明了该算法具有更快预测速度和更低的预测误差。DINH等[14]为了提高交通流预测模型的性能,将SVM算法与K近邻算法相结合,在保证一定准确度的前提下,进一步提高了模型的训练速度和训练规模。RAJALAKSHMI等[15]以多层感知机(Multilayer Perceptron, MLP)算法为模型框架,建立交通流预测模型,并使用粒子群优化算法对MLP算法的权重和阈值进行优化,从而实现动态调整MLP的网络参数。实验结果表明,优化的MLP交通流预测模型具有更稳定的预测效果。
综上所述,机器学习模型有效提升了交通流预测的准确度。但是面对复杂多样的城市道路,需要模型具有更好的通用性和更高的准确度,因此本文使用布谷鸟搜索算法(Cuckoo Search, CS)对SVM模型的重要参数进行优化,以期提高对不同类型城市道路交通流预测的准确度。将青岛市的多组典型城市道路交通流量数据作为研究对象,设置HAM模型、LR模型、MLP模型、RF模型和SVM模型作为对比实验模型,验证CS-SVM模型的优越性。
1 建立预测模型
1.1 SVM模型
SVM模型在被提出后得到了快速的发展。SVM模型被广泛应用于回归分析、文本分类和模式识别等问题中,并取得了良好的效果[16]。其中支持向量机回归(Support Vector Regression, SVR)是SVM的重要分支。SVR模型能够进行回归预测分析,核心思想是让目标集合中所有的点到回归平面的距离最近。
设样本集为A={(xk,yk),k=1,2,3,…,n},将变量x通过非线性变化σ()映射到高维特征空间H中。其次构建线性回归函数g(x)=ωTσ(x)+b,并以此构建二次规划方程如下:
(1)

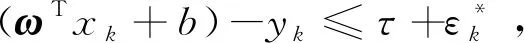
(2)
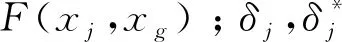
最终将回归问题的求解方程表示为
(3)
1.2 布谷鸟搜索算法
YANG等通过观察自然界中布谷鸟的产卵行为,提出一种优化算法--布谷鸟搜索算法(Cuckoo Search, CS)[17]。CS算法具有较强的全局搜索能力,并且具有内置参数少、计算容易等特点。CS算法的核心思想为:模拟布谷鸟的飞行寻找过程,寻找最为合适的鸟巢用于孵化鸟蛋。
设布谷鸟每次产出α个鸟蛋,在一定鸟巢数量的范围下,鸟巢主人发现鸟蛋不是自己出产的概率为φ(φ∈[0,1])。布谷鸟的搜索过程和孵蛋过程如下:
首先,初始化鸟巢的数量和位置,设鸟巢数量为β。设置适应度函数,并第一次对每个鸟巢的合适程度进行评价。每个鸟巢的主人通过Levy飞行搜索机制对鸟巢进行修补,设搜索最大次数为N。评价修补后的鸟巢与之前鸟巢的合适程度,并按照贪婪法则保留更优的鸟巢,计算过程如下:
ηi,t+1=ηi,t+l·L
(4)
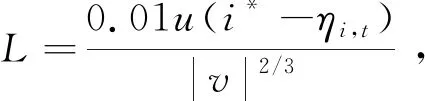
u,v服从的均匀分布函数如下:
(5)
式中:Γ为伽玛函数;λ为调整参数,取值范围为[0,1]。
其次,如果发现外来鸟蛋,鸟巢主人将对鸟巢进行修补,修补的概率为φ。计算过程如下:
ηi,t+1=ηi,t+φ(ηj,t-ηi,t)
(6)
式中:ηj,t为ηi,t邻近的鸟巢;φ取值[0,1]。
最后,鸟巢主人将修补后的鸟巢与当前适合程度最高的鸟巢进行比较,留下适合程度更高的鸟巢进行产蛋孵化。判定是否达到最大搜索次数,若没有达到最大次数则继续以上步骤寻找适合程度最佳的鸟巢;若达到最大次数,则停止搜索开始产蛋孵化。
1.3 基于CS算法优化的SVM模型
SVM模型中的重要参数为C和epsilon。其中C为惩罚系数,体现在对样本中错误数据的容忍程度。当数据较为分散随机时,应将C设置调高,以舍弃更多的数值,提高模型的泛化能力;当数据规律性明显、数据较为统一时,应将C设置调低,保留更多数值的特征,以提高拟合结果的准确度。自由参数通常通过实验和历史经验进行设定,存在不确定性。当模型面对不同城市路段的交通流数据时,往往需要根据数据的特点进行参数调整,因此参数选择很大程度上影响最终预测结果的准确性。
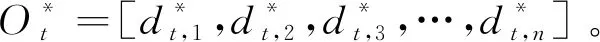
(7)
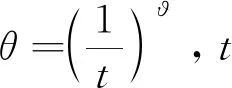
基于上述改进,SVM模型的优化过程如下:
步骤1:将原始交通流数据序列化分组,作为输入数据。设置初始参数的数值,建立SVM模型。
步骤2:将随机生成的β个鸟巢位置设为Wi,t=[xt,c,xt,e],xt,c为第t次迭代i鸟巢的c位置分量,对应SVM的参数C;xt,e为第t次迭代i鸟巢的e位置分量,对应SVM的参数epsilon。计算鸟巢位置的适应度函数,将Wi,t作为当前的最适合鸟巢。
步骤3:对鸟巢进行修补和位置更新,并对更新的位置加入扰动因子。将加入扰动因子的最新鸟巢位置和上一个鸟巢位置进行对比,保留适应度更高的鸟巢位置,作为当前的最佳鸟巢。
步骤4:判定是否达到设定的最大搜索次数,如果没有达到最大次数则重复上述步骤;如果达到最大次数,则停止训练,并将当前计算的鸟巢位置作为最佳结果。
步骤5:将最佳鸟巢位置分量作为SVM模型的对应参数C和epsilon。对每一组城市道路交通数据进行训练,获取预测结果,从而建立基于CS-SVM模型的短时交通流预测模型。优化过程流程如图1所示。
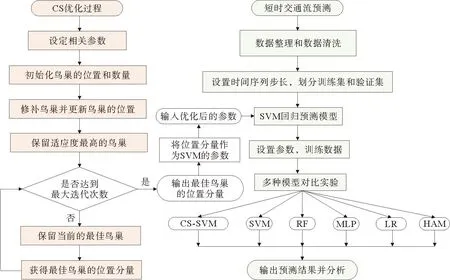
图1 优化过程流程
2 实验数据及参数设置
选择青岛市即墨区的城市交通流量数据作为研究对象。数据的收集时间为2021-10-31-2021-11-13,总计14 d。交通流量数据的时间间隔为5 min,每个路段的数据量为4032个。将收集的数据进行整理和清洗。对于数据出现空缺的问题,考虑到交通流数据具有周期性和规律性,且车流量的变化是随时间变化而逐渐增减的,因此将空缺位置附近两个数据的平均值作为填补数据。并设置有效数据区间,去除无效数据。为检验本文提出的模型具有广泛适用性,收集4个不同路段的交通流量数据进行研究。4个不同的典型城市路段如下:
即兰路:双向六车道,为地面开放式道路。最高车辆数为81辆。车流量稀疏,邻近郊区。
青威路:双向八车道,为地面开放式道路。最高车辆数为145辆。邻近学校,潮汐特征明显。
墨城路:双向六车道,为地面开放式道路。最高车辆数为139辆。邻近商业区。
海尔路:双向六车道,道路延伸处与多条纵向干线以非立体交通的形式交汇。最高车辆数为122辆。
即兰路(JLR)、青威路(QWR)、墨城路(MCR)和海尔路(HER)的数据信息见表1。

表1 路段数据信息
CS-SVM模型的对比模型设置为:HAM模型、LR模型、MLP模型、RF模型和SVM模型。将时间步长设置为12(12×5=60 min)。MLP模型的学习率设置为0.0001,一次性的投放抓取次数设置为128。所有模型训练集和测试集的比例为0.2。训练轮数epoch设置为300。CS-SVM模型的鸟巢数量设置为20,最大飞行搜索次数设置为100,扰动系数ϑ取值为0.5。
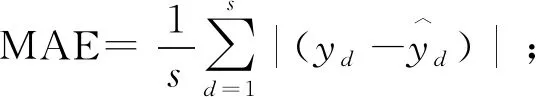
3 预测结果分析
表2为所有模型的短时交通流预测结果。从表2可以看到,CS-SVM模型的预测误差明显低于其他对比模型。其中相比传统数理统计和回归分析模型,CS-SVM具有显著的提升。4个路段的MAE值,CS-SVM相比HAM模型和LR模型平均下降了39.62%和31.59%。4个路段的RMSE值,CS-SVM相比HAM模型和LR模型平均下降了38.64%和29.11%。此外,CS-SVM具有比传统机器学习模型更高的准确度。CS-SVM模型相比MLP模型和RF模型的MAE值平均下降了20.10%和10.04%,相比MLP模型和RF模型的RMSE值平均下降了19.84%和9.54%。同时,CS-SVM模型相比没有加入CS算法优化的SVM模型,在MAE值上4个路段平均下降了6.56%,在RMSE值上4个路段平均下降了7.36%。可见本文提出的CS-SVM模型具有更高的准确度和更广泛的适用性。
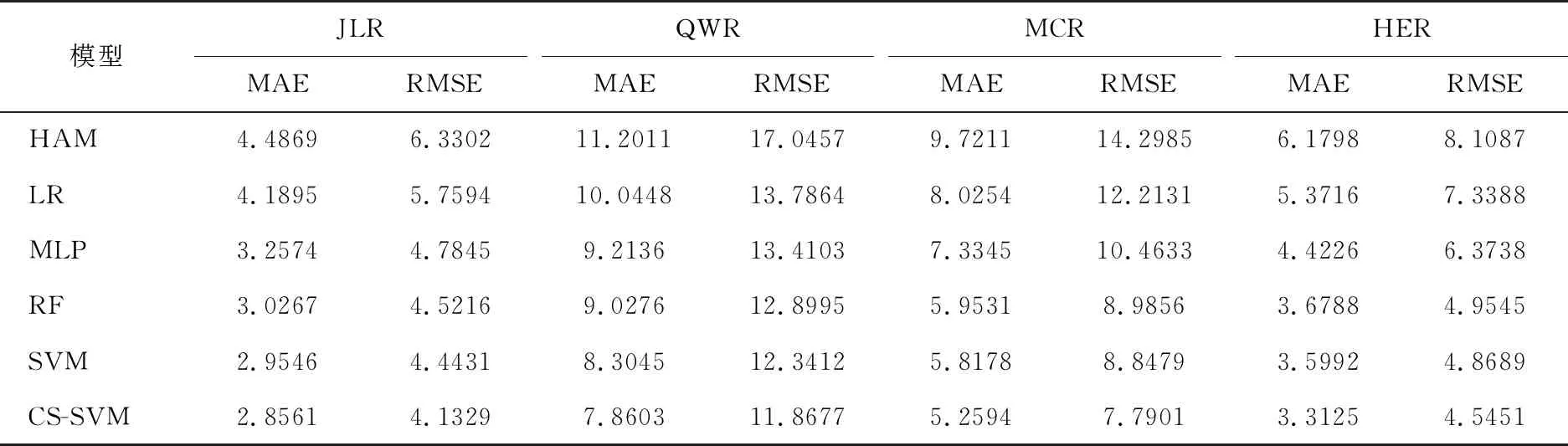
表2 短时交通流预测结果
图2为CS-SVM算法优化过程中的迭代次数和适应度值变化曲线。
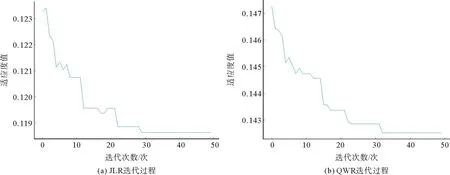
图2 迭代次数和适应度值
由图2可以看出,4个路段的CS-SVM算法均在35次以内求出了最佳适应度鸟巢位置。因此CS-SVM算法在参数优化过程中能够快速收敛。并且在面对不同路段时,CS-SVM算法均能表现出良好的优化效果,具有高效稳定的优点。
4 结束语
为了提高交通流预测模型的准确度和适用性,本文使用CS算法对SVM的重要参数进行优化。同时为了进一步提高CS算法的优化效果,加入扰动因子加强CS算法寻找鸟巢位置的随机性和变异能力。为验证CS-SVM模型的预测效果,选用4组青岛市的典型城市交通流量数据作为研究对象,并与HAM模型、LR模型、MLP模型、RF模型和SVM模型进行对比。实验结果表明,CS-SVM模型具有更小的预测误差,并且面对4条不同的路段均能表现出良好的模型性能。因此,本文提出的CS-SVM模型能够有效提升短时交通流预测的准确度,能够为交通组织优化、居民出行选择和交通流理论研究等方面提供相应的帮助。

