2023年二次函数中考题新趋势

吴琨

中考考查二次函数知识的题型结构基本保持不变，试题特点体现在起点低、尾巴高，根植于教材。不过，近年来的命题增加了思维的含量，体现学以致用与实践的能力。现以江苏省的部分中考题为例加以分析。

一、让数与代数的考查更灵活

例1 （2023· 江苏泰州）二次函数y=x2+3x+n的图像与x轴有一个交点在y轴右侧，则n的值可以是。（填一个值即可）

【解析】设二次函数y=x2+3x+n的图像与x轴交点的横坐标为x1、x2，则二元一次方程x2+3x+n=0的根为x1、x2。

由根与系数的关系，得

x1+x2=-3，x1?x2=n。

∵一次函数y=x2+3x+n的图像与x轴有一个交点在y轴右侧，∴x1、x2异号。∴n＜0。

故答案为：-3（答案不唯一）。

【点评】本题考查抛物线与x轴的交点求法以及根与系数之间的关系。解题的关键是要理解根与系数之间的关系，这样才能灵活应用到解题过程中。

二、存在性问题或动点问题的考查更全面

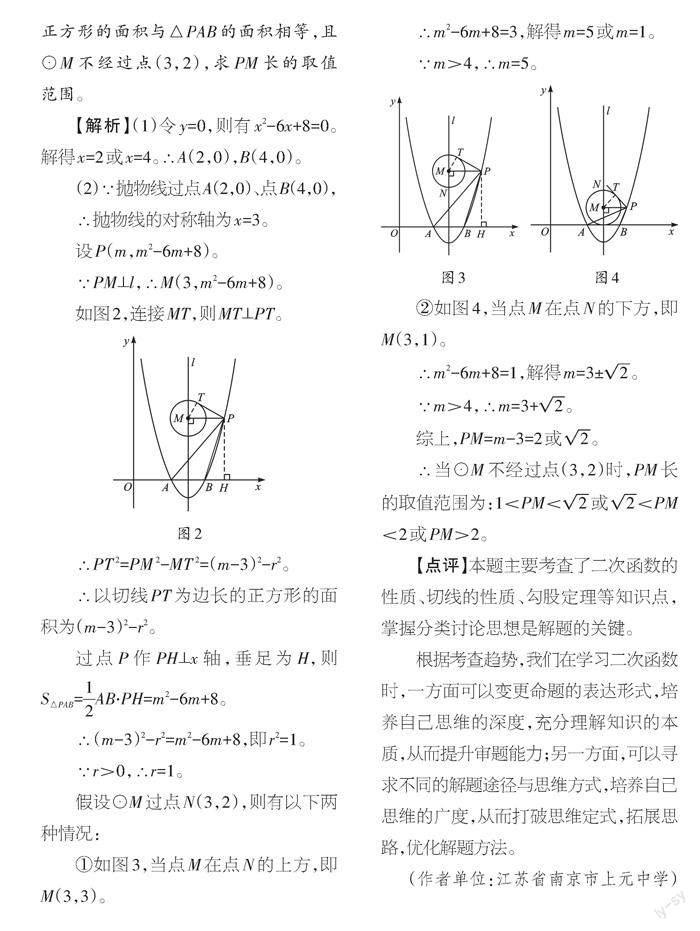
例2 （2023· 江苏苏州）如图1，二次函数y=x2-6x+8的图像与x轴分别交于点A、B（点A在点B的左侧），直线l是对称轴。点P在函数图像上，其横坐标大于4，连接PA、PB，过点P作PM⊥l，垂足为M，以点M为圆心，作半径为r的圆，PT与⊙M相切，切点为T。

（1）求点A、B的坐标；

（2）若以⊙M的切线长PT为边长的正方形的面积与△PAB的面积相等，且⊙M不经过点（3，2），求PM长的取值范围。

【解析】（1）令y=0，则有x2-6x+8=0。解得x=2或x=4。∴A（2，0），B（4，0）。

（2）∵抛物线过点A（2，0）、点B（4，0），

∴抛物线的对称轴为x=3。

设P（m，m2-6m+8）。

∵PM⊥l，∴M（3，m2-6m+8）。

如图2，连接MT，则MT⊥PT。

∴PT 2=PM 2-MT 2=（m-3）2-r2。

∴以切线PT为边长的正方形的面积为（m-3）2-r2。

过点P作PH⊥x轴，垂足为H，则S△PAB=[12]AB?PH=m2-6m+8。

∴（m-3）2-r2=m2-6m+8，即r2=1。

∵r＞0，∴r=1。

假设⊙M过点N（3，2），则有以下两种情况：

①如图3，当点M在点N的上方，即M（3，3）。

∴m2-6m+8=3，解得m=5或m=1。

∵m＞4，∴m=5。

②如图4，当点M在点N的下方，即M（3，1）。

∴m2-6m+8=1，解得m=3±[2]。

∵m＞4，∴m=3+[2]。

综上，PM=m-3=2或[2]。

∴当⊙M不经过点（3，2）时，PM长的取值范围为：1＜PM＜[2]或[2]＜PM＜2或PM＞2。

【点评】本题主要考查了二次函数的性质、切线的性质、勾股定理等知识点，掌握分类讨论思想是解题的关键。

根据考查趋势，我们在学习二次函数时，一方面可以变更命题的表达形式，培养自己思维的深度，充分理解知识的本质，从而提升审题能力；另一方面，可以寻求不同的解题途径与思维方式，培养自己思维的广度，从而打破思维定式，拓展思路，优化解题方法。

（作者单位：江苏省南京市上元中学）