基于数理统计方法的水质总氮校准曲线残差值检验

杨玉凤

(昆明滇池水务环境监测有限公司，云南 昆明 650200)

在化验检测的实践过程中，最重要的一点是要采取有效措施保证所得到的数据和资料的可靠性。现代化验检测工作中，绝大多数使用仪器分析方法，一些仪器需要建立分析信号与分析物量值(质量或浓度)之间的相关关系，即建立校准曲线。其中，确保用于建立校准曲线数据的可靠性是仪器分析获得准确定量分析结果的前提条件。

校准曲线的拟合是建立在回归分析的理论基础上，通过最小二乘法估计其参数。采用普通最小二乘法拟合校准曲线应满足以下假设条件[1-2]：①正态性假设，即其因变量y的随机误差项εi服从均值为0，方差为σ2的正态分布；②独立性假设，即其因变量y的随机误差项之间相互独立，满足COV (εi,εj)= 0(i≠j)；③同方差性假设，即其因变量y的随机误差项εi的方差都相同。

由于校准曲线估计结果的正确性与可靠性需建立在一系列假定基础之上。为此，本文从工作需要出发，利用实际工作中所得数据，结合文献资料，以水质中总氮测定为例，着重对校准曲线残差值各假定条件的检验方法进行探讨。

1 材料与方法

1.1 仪器与试剂

TU1810PC紫外可见分光光度计(北京普析通用仪器有限公司)，用于水质总氮的测定。

硝酸盐氮溶液(102119#)：证书号GSB 05-1144-2000，500 mg/L，相对扩展不确定度2%，k=2，环境保护部标准样品研究所提供。

1.2 实验方法

总氮检测方法依据为 HJ 636—2012《水质 总氮的测定 碱性过硫酸钾消解紫外分光光度法》[3]。

2 数据的收集及检验

2.1 数据收集

依据GB/T 22554—2010《基于标准样品的线性校准》[4]规定：①每个标准样品应至少测量2次(建议实际中尽可能多次重复)；②所有标准样品的重复测定数应相等；③重复测量所用时间和条件的覆盖范围应尽可能放宽，以确保所有操作条件的代表性。

本文数据来源于2022年内对总氮项目不同质量浓度硝酸盐氮标准使用液进行k=6次测定，数据收集结果见表1。各曲线点一年内累计的残差值，结果见表2，残差值样本量n=48。

表1 各质量浓度点6次测定所得数据及曲线拟合

表2 残差值汇总

2.2 正态性检验

一般情况下，如果因变量的随机误差项εi是由许多微小的独立随机因素影响的结果，那么就可以认为εi具有正态分布。

一般检测中，在进行校准曲线的拟合时，总是假定数据来源于正态总体，但此假定是否成立，需要对测得数据进行正态性检验。本文将介绍QQ图法，该方法可直观的判断数据分布是否近似于正态分布，同时介绍AD法，该方法通过计算出检验统计量 A2*来检验数据是否服从正态分布。

2.2.1 QQ图法

对应于正态分布的QQ图，是由标准正态分布的(修正)分位数为横坐标，样本值为纵坐标绘制而成的散点图。要利用QQ图鉴别样本数据是否近似于正态分布，只需看QQ图上的点是否近似地在一条直线附近[5]。本文操作步骤为[6]：①将残差值按升序j排列；②计算P(Z)=(j-0.5)/48; ③根据P(Z)值，通过Excel函数“NORM.S.INV”求出标准正态分布的(修正)分位数Zj，列于表3中；④依据表3的数据，以Zj为横坐标，eik为纵坐标绘制图1。由图1看出，各点近似地在一条直线附近，说明该样本残差值服从正态分布。

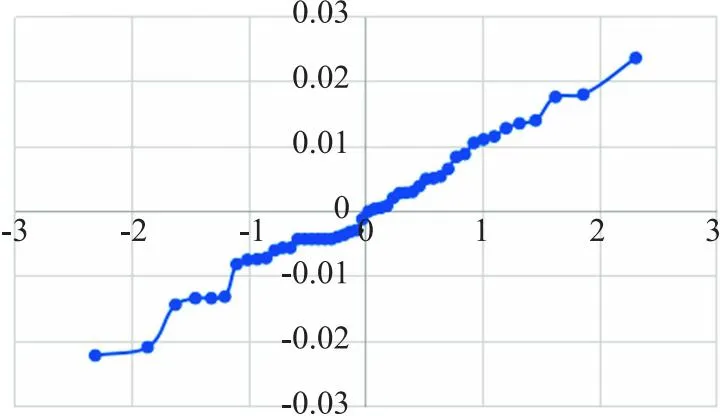
图1 QQ图

2.2.2 AD检验法

AD检验是正态性检验的一种，能够在较小样本(n>5)的情况下，对数据正态性进行检验。其原理是通过计算样本分布函数(CDF)和经验概率密度函数(EDF)之间的二次 A-D 距离来衡量样本是否属于某一特定分布族[7]。本文操作步骤为：①假设该样本残差值服从正态分布(原假设H0)；②将残差值eik按照升序j排列为ej；③计算残差值的均值和方差；④计算累计分布函数F(ej)；⑤通过公式(1)计算A2；⑥通过公式(2)计算修正过的检验统计量A2*；⑦查AD检验临界值表，如果A2*>0.752就可判定在 5%的显著性水平下拒绝正态性假设，如果A2*<0.752，就可判定在 5%的显著性水平下不能拒绝正态性假设。用于计算A2的数值见表4，最终结果为A2=0.3527，A2*=0.3586，小于0.752，可判定在5%的显著性水平下不能拒绝正态性假设，此结论与绘制QQ图所得结论一致。

(1)

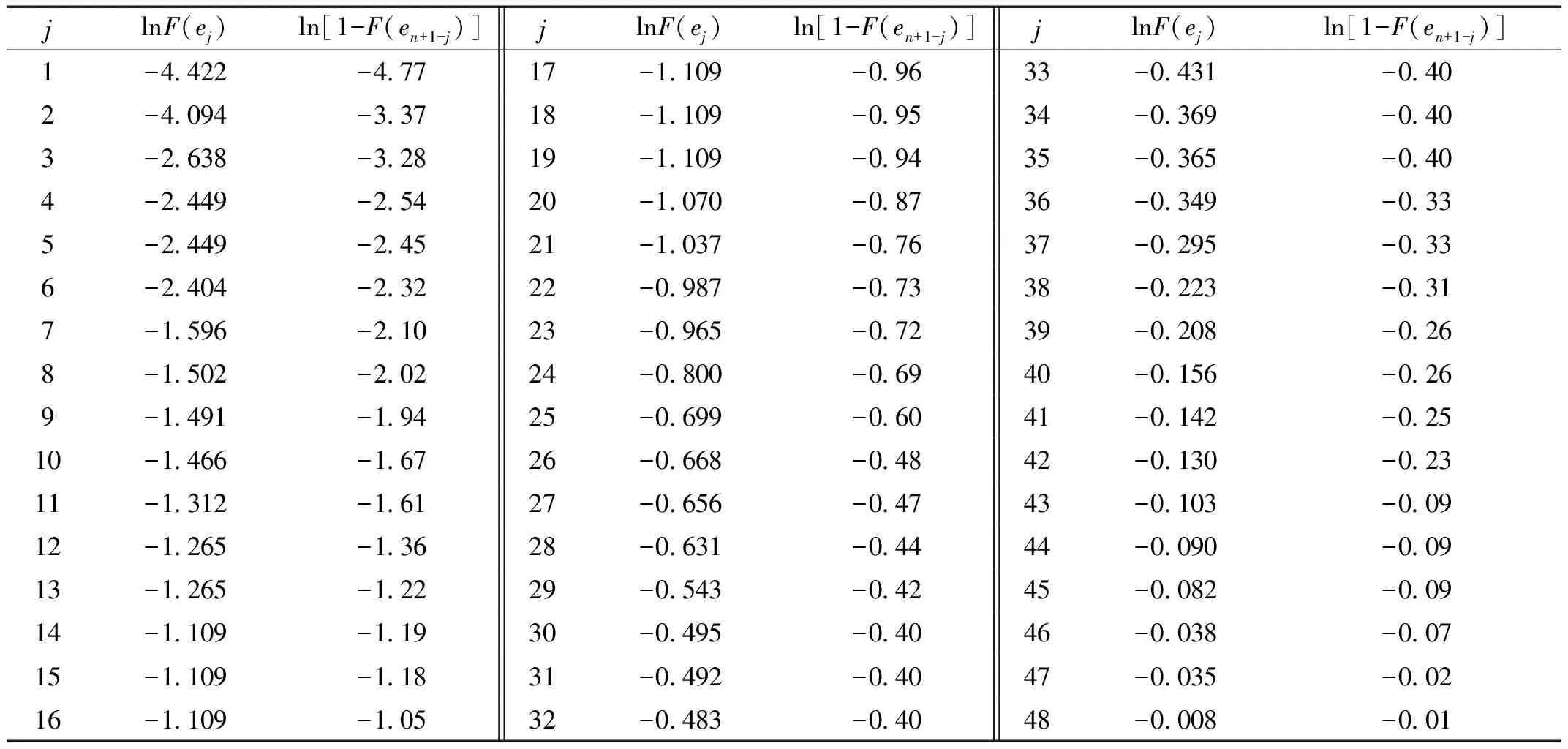
表4 AD检验计算数据

(2)

2.3 独立性检验

本文将介绍图示检验法，该方法可直观地对数据独立性进行判断。同时介绍DW检验法，该方法通过计算出检验统计量DW值，从而检验数据是否存在序列相关。需要注意的是，回归模型中残差值之间出现自相关现象，指的是残差值前后期数值之间的相关关系[2]。

2.3.1 图示检验法

图示检验法是一种直观的诊断方法。本文操作步骤为：①将残差值eik按测定时间t的先后顺序进行排列，以表5中的et表示；②依据表5中数据(et，et-1)绘制图2。如果大部分点落在第1、3象限，表明残差值存在正的序列相关；如果大部分点落在第2、4象限，表明残差值存在负的序列相关[2]。图2中大部分点落在1、3象限，但也有部分点落在2、4象限，初步推断残差值存在正的序列相关，需进一步通过DW检验进行验证。

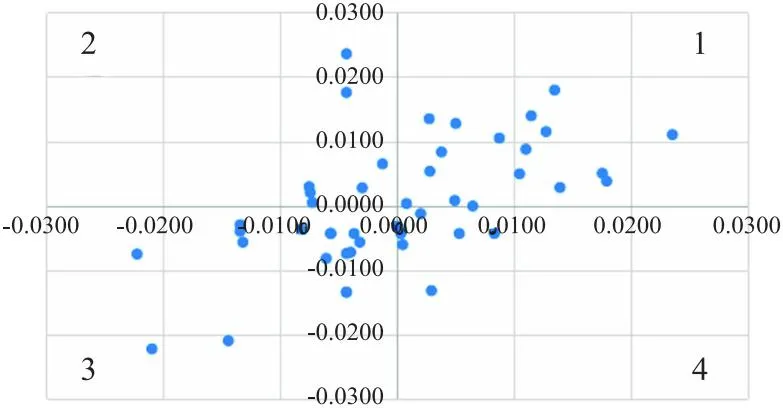
图2 (et，et-1)散点图

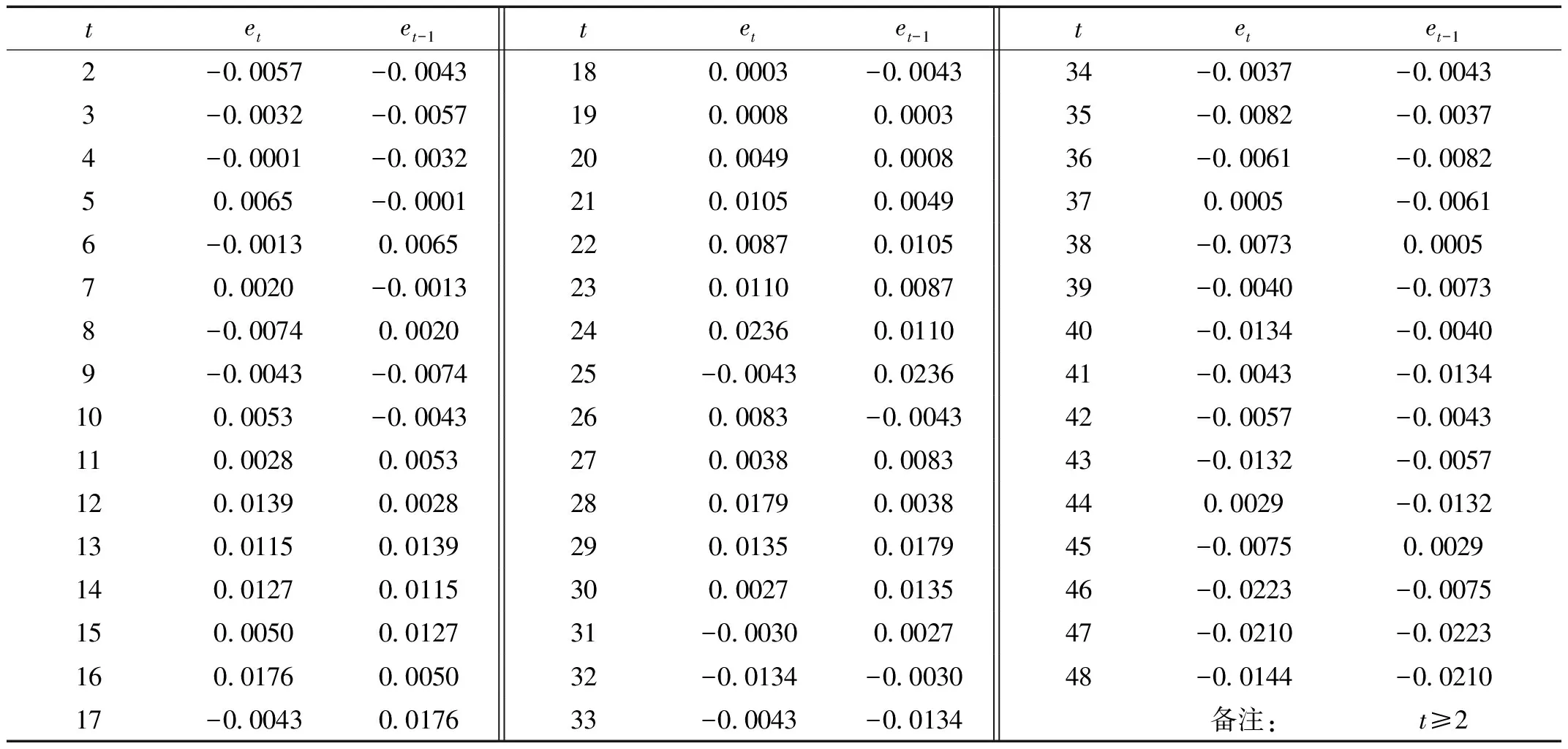
表5 (et，et-1)数据

2.3.2 DW检验法

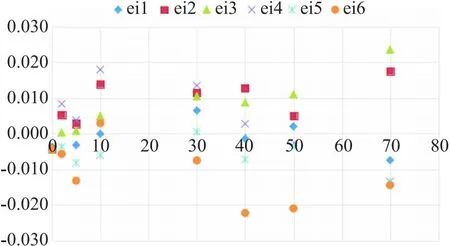
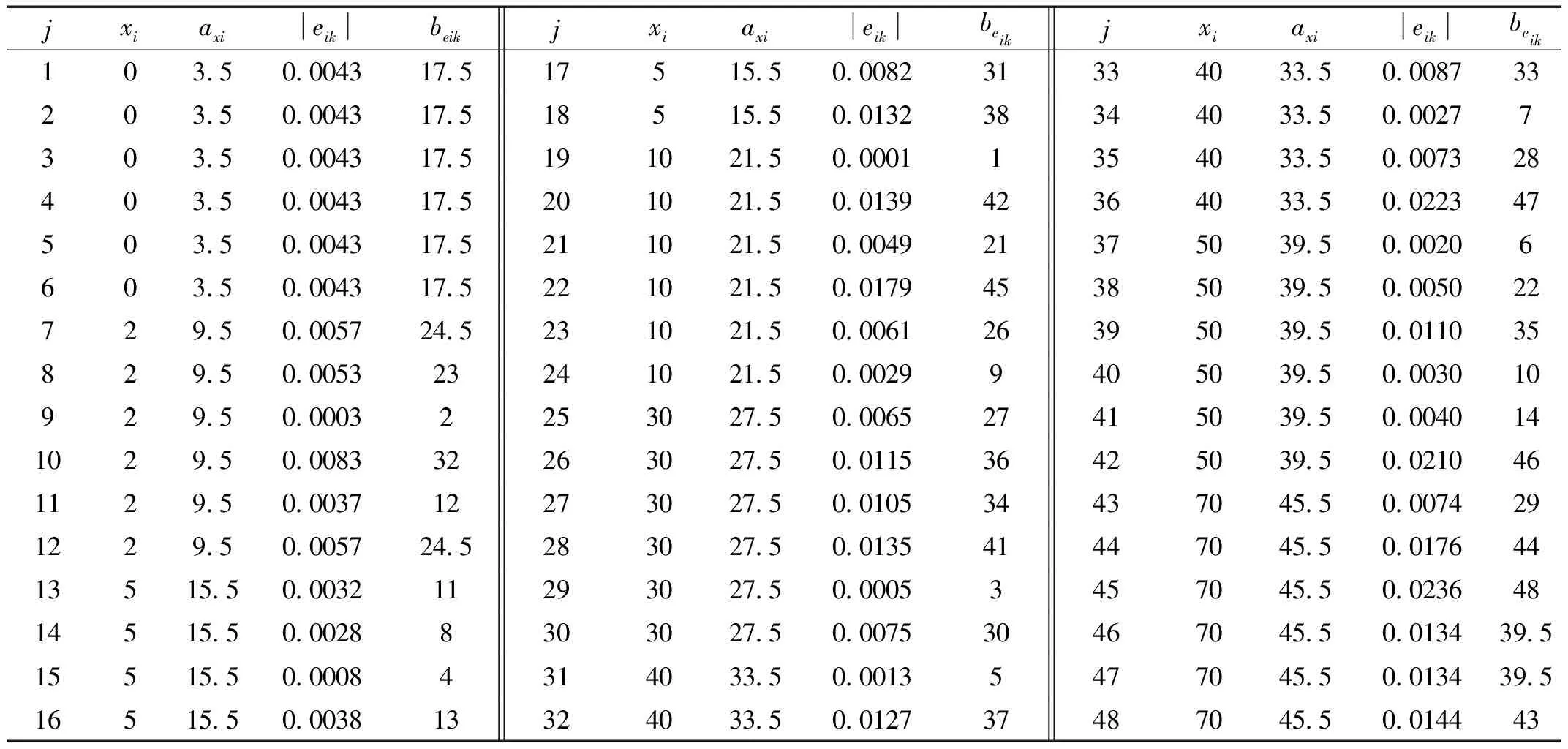
DW统计量只可检验残差值具有一阶自回归形式的序列相关。本文操作步骤为：①假设残差值不存在序列自相关(原假设H0)；②应用表5中数据，通过公式(3)计算得ρ值为0.561，通过公式(4)计算得DW值为0.877；③根据样本量为48，解释变量数目为2，在5%的显著性水平下查DW分布表，确定检验临界值dL为1.49>0.877；④查DW检验判别表[8]，当0

(3)

DW≈2(1-ρ)

(4)

2.4 同方差性检验

异方差是与同方差相对而言的，同方差即是指线性回归模型的随机干扰项的方差全部等于一个有限的常数，而异方差现象可表述为线性回归模型中随机干扰项的方差不再是某一相等的常数，而是随着观察点的变化而变化[9]。

对异方差的检验，本文将介绍残差图法，该方法可对异方差现象进行直观判断。同时介绍等级相关系数法，该方法通过计算出等级相关系数，随后计算t统计量，从而检验数据是否存在异方差现象。

2.4.1 残差图法

残差图反映出的现象一般非常简单、直观，但因每个人的主观判断不同，残差图只能作为一种非正式的检验方法。本文操作步骤为：①依据表2中数据，以残差值eik为纵坐标，以自变量xi为横坐标绘制散点图，得图3。②根据各点的分布情况判断是否出现异方差现象，如果校准曲线残差值eik存在异方差性，残差图上各点的分布会呈一定的走势，例如残差eik的值随xi值的增大而增大(或减小)，呈现出明显的规律。由图3看出，随xi值的增大图中各点的离散程度有增大的趋势，说明有可能存在异方差现象，但需进一步使用等级相关系数法进行验证。

图3 残差图

2.4.2 等级相关系数法

等级相关系数法使用的是非参数检验方法[10]，其思路是将异方差性与扰动项εi和自变量xi之间的相关程度挂钩[11]。由于扰动项无法观测，就用残差值eik代替。本文操作步骤为：①取eik的绝对值|eik|，把数据对(xi，|eik|)按序号j排列于表6中。②通过EXCEL函数“RANK.AVG”，分别计算xi，|eik|的等级秩次axi、beik。③在xi与|eik|中无相同秩次的情况下，按式(5)计算等级相关系数；在xi与|eik|中有相同秩次的情况下，按式(6)～(8)计算等级相关系数[12]。④由于本文中xi与|eik|中有相同秩次，应用表6中数据按式(6)～(8)计算等级相关系数，得rs校正=0.402。⑤假设残差值eik与自变量xi之间无相关(原假设H0)。⑥对等级相关系数rs校正进行显著性检验，按照式(9)计算得t=2.98，查t分布临界值表，t0.025，46=2.32，得t>t0.025，46，拒绝原假设，说明该样本残差值存在异方差现象。等级相关系数法的检验结果对残差图检验法的判断结果进行了有效佐证。

(5)

表6 等级秩次数

(6)

(7)

(8)

(9)

备注:axi为的等级秩次;beik为|eik|的等级秩次

3 讨论

3.1 正态性假设相关问题

采用普通最小二乘法拟合校准曲线，在其它假定条件满足时，非正态性对最小二乘法估计和总变异的分解影响不大，其结果仍是最优线性无偏的，但将对参数估计值的著显性检验和置信区间的估计带来影响[13]。若检验发现因变量y的随机误差项εi不服从正态分布，通常采用对因变量y进行变换的方法，将其数据转换成正态分布。但同时需注意，在数据转换时已将数据蕴含的原始信息进行了改变，由此得到的曲线回归结果，其参数的解释意义已和变换前有所不同。

3.2 独立性假设相关问题

一个线性回归模型的随机误差项εi存在序列相关时，如果仍然使用普通最小二乘法估计未知参数，将会产生如下后果[2]：①参数的估计值不再具有最小方差线性无偏性；②均方误差(MSE)可能会严重低估误差项的方差；③容易导致对回归方程进行检验的F检验和t检验失效；④最小二乘估计量对抽样波动非常敏感；⑤利用回归模型进行预测和结构分析将会带来较大的方差甚至错误的解释。当线性回归模型的随机误差项εi存在序列相关性时，需要查明引起随机误差项εi产生序列相关性的原因：如果是因回归模型选用不当，则应该改用适当的回归模型；如果是因缺少重要的自变量，则应该增加自变量；如果以上两种方法都不能消除随机误差项εi的序列相关性，则需采用迭代法、差分法等方法进行处理。

3.3 同方差性假设相关问题

一个线性回归模型的随机误差项εi不满足同方差性，即存在异方差现象时，仍使用普通最小二乘法估计回归参数，将会出现的问题[2]：①参数估计虽然是无偏的，但不是最小方差线性无偏估计；②参数显著性检验失效；③回归方程应用效果不理想。线性回归模型的随机误差项εi存在异方差性现象时，可采用以下两种方法进行处理：①对因变量y作适当的变换，使方差趋于稳定。这是由于因变量的变化范围愈大，随机误差项εi的异方差性一般也愈明显，因此，采用适当形式缩小因变量y的变动幅度，可在一定程度上消除异方差性[14]。②使用加权最小二乘法进行校准曲线拟合。

3.4 校准曲线拟合优度检验相关问题

由于在实际检测过程中，线性校准曲线两端，即高浓度和低浓度范围内有时会出现不同程度的弯曲，影响校准曲线预测的准确性，因此需要对该现象进行检验，即进行校准曲线拟合优度的检验，从而确定校准曲线的直线范围。GB/T 22554—2010《基于标准样品的线性校准》[4]介绍了通过建立方差分析(ANOVA)表的方式，对校准曲线拟合优度进行检验。同时提到随机误差项εi的正态性及独立性影响到方差分析法的有效性。因为对单因素多水平设计定量资料进行一元方差分析的前提条件是定量数据应具有独立性、正态性和方差齐性[15]。因此，对校准曲线拟合优度进行检验前，需对该曲线随机误差项εi的独立性、正态性和方差齐性进行验证，以保障校准曲线拟合优度检验的可靠性。

4 结论

一般检测过程中人们重点关注校准曲线的判定系数，本文中校准曲线判定系数r2=0.9997，已满足相关标准[3]要求，但由上文检验结果可以了解到该曲线残差值满足正态性，不满足独立性和同方差性，而不满足相关假设条件将会产生一系列不良后果。故检测工作中，检测人员在采用普通最小二乘法拟合校准曲线时，应考虑到应用普通最小二乘法的前提假设条件是否满足，不能盲目默认相关假定条件成立，应将数理统计理论与化验检测实际相结合，保障曲线拟合的可靠性。同时，应该注意到对相关假定条件进行检验时，图示检验法一般比较简单直观，但存在各人主观判断差异的问题，而通过计算统计量值的方法，可以得到定量的判断依据，避免了因主观判断引起的误差。