工艺参数对不锈钢管切割表面质量的影响研究*

李和伟,孙兴伟,杨赫然,董祉序,刘 寅

(沈阳工业大学机械工程学院,沈阳 110870)

0 引言

不锈钢由于含有大量的Cr、Ni、Mn等元素,具有高强度、低膨胀系数、耐腐蚀性和良好的热导率等特点,广泛用于石油、化工、锅炉、电力、建筑、机械、汽车、船舶以及航空、航天等行业[1]。然而,在不锈钢管的切断加工过程中,工件边缘附近存在毛刺产生的现象,导致工件的切口质量较低并增加去除毛刺的成本[2]。为最小化去毛刺的成本,需分析毛刺的形成机理,并了解材料、刀具和加工条件等对毛刺尺寸的影响机理,从而抑制毛刺的形成[3]。根据毛刺生成位置的不同,对毛刺进行分类。由于不同种类的毛刺其形成机理也不尽相同,因此建立相应的理论模型来分析毛刺的形成机理是至关重要的[4]。通过建立毛刺形成的数学模型,才能进一步研究切削参数对毛刺尺寸大小的影响规律[5-6]。除此之外,建立有限元仿真模型也是分析毛刺尺寸变化规律的有效方法[7-8]。本文通过建立顶边毛刺形成的解析模型,描述毛刺的产生过程,并提出毛刺形成的影响因素。随后,运用有限元仿真软件,建立三维切削仿真模型,模拟不锈钢管的切削过程,得出毛刺的尺寸大小。与相同加工条件下切割不锈钢管得到的毛刺尺寸进行对比,验证了有限元仿真模型的有效性,能借助有限元仿真模型对不同工艺参数下的毛刺尺寸进行预测[9-11]。

本文采用建立解析模型、有限元分析与毛刺尺寸测量试验相结合的方法,对不锈钢管切口毛刺的形成及特征进行研究,为抑制切口毛刺的产生和优化工艺参数提供理论指导。

1 切口毛刺形成的解析模型

切口毛刺的形成过程如图1所示,刀具刚切入工件时会产生一初始空腔,加工表面因产生塑性变形而凸起,如图1a所示。切削距离增加,初始空腔扩张,一部分材料沿着刀具前刀面向上运动,形成切屑,如图1b所示。切削距离进一步增加,连接切屑和工件的材料继续拉伸,直到断裂,如图1c所示。当切屑与工件表面分离时,一部分材料残留在零件边缘,形成顶边毛刺,如图1d所示。

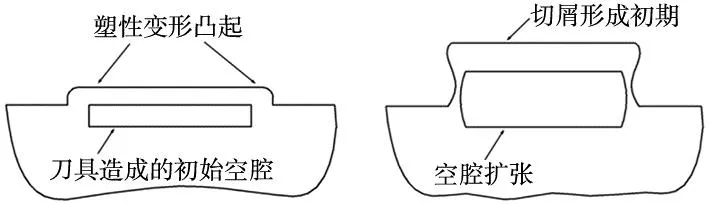
(a) 初始空腔形成 (b) 空腔扩张

图2为工件切削模型,剪切面上的剪切力和刀具前刀面的作用力处于动态平衡状态。ab为主剪切面,τ为在该平面上达到材料的屈服剪应力,Fs为主剪切面上的剪切力。剪切力Fs可表示为:

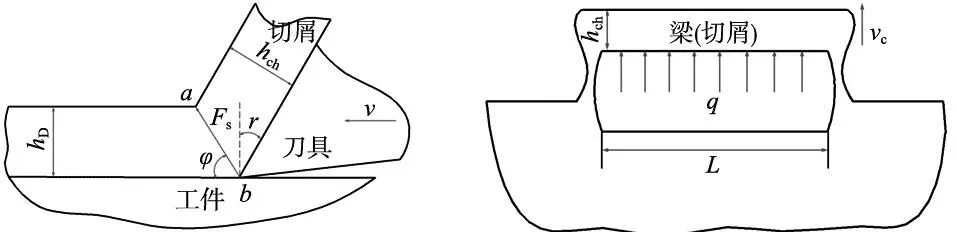
图2 工件的切削模型 图3 切屑与工件分离模型

(1)

式中:As为剪切平面的横截面积,AD为切削层横截面积,bD为切削宽度,hD为切削层的厚度,φ为剪切角。

根据金属切削原理,切削层的厚度hD与切屑厚度hch的关系可表示为:

(2)

式中:γ为刀具前角。

假设在切屑与工件分离的过程中,切屑是一个两端完全固定的矩形梁。如图3所示,梁的深度为hch,梁的长度为L,均匀载荷q施加在梁上,载荷的速度为vc。

梁的动量可表示为:

Fst=mvc

(3)

式中:m为有效质量。

切屑的塑性极限弯矩可表示为:

(4)

式中:σs为材料的屈服强度。

在工件切削过程中,当剪切面的剪切力达到Fs时,切屑受到剪切力的作用与工件分离,则剪切力对切屑与工件分离作用程度可表示为:

(5)

由于剪切平面只受到剪切力的作用,结合米塞斯屈服准则,材料的屈服剪应力τ与材料的屈服强度σs可表示为:

(6)

将式(5)代入式(6),得到剪切力对切屑与工件分离作用程度的表达式:

(7)

根据式(3)与式(7)可知,切削速度、刀具前角、每转进给量(切削厚度)是切口毛刺形成的重要影响因素,在仿真过程中采用单因素控制变量的方法研究单个因素对毛刺尺寸大小的影响规律。建立的毛刺解析模型可为探寻不同工艺参数对毛刺尺寸的影响规律提供理论依据。

2 有限元模型

有限元切削仿真结合理论计算和仿真分析为一体,并采用实验观测的方法加以验证,可以进行切削加工过程的研究,以及预测切削加工中各关键物理量的变化。

2.1 模型设置

刀具的结构参数如表1所示,根据结构参数建立刀具的三维模型。

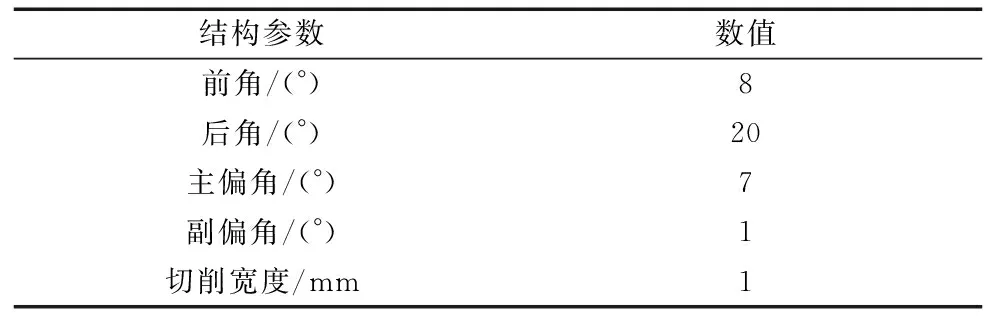
表1 刀具的结构参数

由于工件为回转体,为简化仿真过程,取工件周向的1/36(角度为10°)进行仿真。刀具与工件的装配模型如图4所示,工件固定不动,其底部边界条件设置为完全固定,刀具沿工件圆周方向以给定的切削深度及切削速度进行切削。

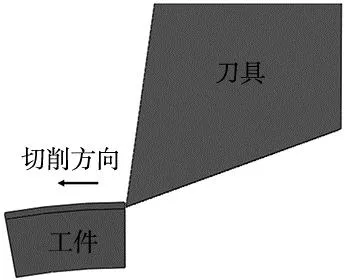
图4 切削仿真模型

2.2 材料属性及摩擦模型设置

在金属材料切削加工中存在应变硬化效应、应变率强化效应和热软化效应[12]。Johnson-Cook模型能够反映出大应变、大应变率和高温情况下的金属本构行为。Johnson-Cook模型可以表示为:

(8)

工件材料为316L不锈钢,该材料的Johnson-Cook本构模型参数如表2所示。

表2 316L的Johnson-Cook本构模型参数

有限元分析的精度与材料力学性能的准确性密切相关,因此需要准确设置工件和刀具的材料特性。工件及刀具的热和机械性能如表3所示。

表3 316L不锈钢及硬质合金刀具的物理参数

工件在切削加工过程中,刀具的前刀面对切屑以及刀具的后刀面对工件已加工表面均存在摩擦和挤压作用。同时,在切削过程中切屑、刀具和工件之间会引起温度、应力和应变的重新分布,使工件产生塑性变形。因此,建立合理的摩擦模型是切削仿真成功实现的关键因素[13]。建立的摩擦模型是粘滑混合方程,其中粘摩擦由上边界条件决定,上边界的值设置为材料剪切强度。在滑动区域中应用经典库仑摩擦,其值设置为0.3。摩擦模型可以表示为:

(9)

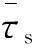
2.3 韧性断裂准则设置

在有限元分析时,当刀具与工件接触节点的等效塑性变形达到所设置的材料等效塑性应变值时,相应的网格单元被删除,从而实现切屑与工件分离。

本文采用Johnson-Cook损伤演化作为韧性断裂准则。Johnson-Cook失效模型基于累积损伤,当损伤参数ω达到或超过1的值时,材料发生断裂。ω可表示为:

(10)

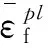
(11)

式中:pf为压应力,qf为米塞斯应力,d1～d5为材料失效参数。

Johnson-Cook失效模型参数的是在转变温度或低于转变温度的条件下,通过工件的高温拉压扭转实验获得的参数[14]。d1～d5的取值如表4所示。

表4 316L不锈钢的失效模型参数

图5展示了在前角γ=8°、每转进给量f=0.02 mm/r和切削速度v=40 mm/s工艺参数条件下,得到毛刺尺寸的试验值与仿真值,两者大小基本一致,说明考虑毛刺形成和几何形状的模型的临界损伤值是准确的,同时也验证了仿真模型的准确性。

(a) 仿真模拟毛刺尺寸 (b) 试验毛刺尺寸图5 毛刺仿真值与试验值对比

2.4 毛刺仿真尺寸的评估方法

通常以厚度值和高度值作为衡量毛刺尺寸大小的标准,图6a展示了毛刺形成的几何特征和位置,以高度和根部厚度为衡量标准来估计毛刺尺寸,如图6b所示。

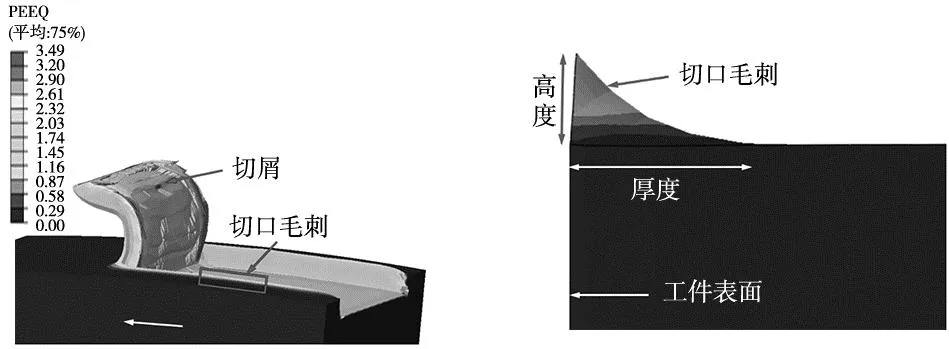
(a) 切口毛刺形成的位置 (b) 毛刺尺寸图6 毛刺的几何特征和位置

如图7所示,毛刺分布在顶部边缘,而毛刺尖端是沿切削方向随机变形凸起的。为获取准确的结果,在切削稳定区域毛刺尖端处均匀选取18个点,求取平均值,即为毛刺的高度值。同理,可得出毛刺的根部厚度值。

图7 切削稳定区域毛刺高度尺寸测量点布置

3 结果与讨论

3.1 毛刺形成过程

通过分析毛刺生成区域的连续应力变化和塑性变形可研究毛刺的形成机理。进一步分析表明,切口毛刺的形成过程可分为3个阶段:变形凸起开始阶段、变形凸起形成阶段和毛刺形成阶段。

在前角γ=8°、每转进给量f=0.02 mm/r和切削速度v=40 mm/s工艺参数条件下,工件材料的变形凸起开始阶段如图8所示。刀具的前刀面在横截面a-a′处挤压工件材料,工件材料侧向流动至切口边缘处,产生轻微的凸起,在未切削表面引起弹性变形和局部塑性变形,如图8右图所示。与此同时,切屑开始形成,该阶段标志着切口毛刺的基体变形开始。

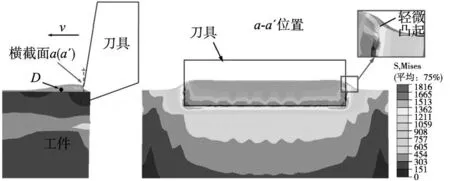
图8 毛刺变形凸起开始阶段

工件材料的变形凸起形成阶段如图9所示,刀具沿切削方向继续切入工件达到横截面b-b′处时,工件材料的变形凸起不断增大,切口边缘处产生较大的塑性变形,如图9右图所示,随着刀具的进一步深入,切削层的材料与工件基体进一步被拉伸,该阶段标志着切口毛刺的基体变形形成。

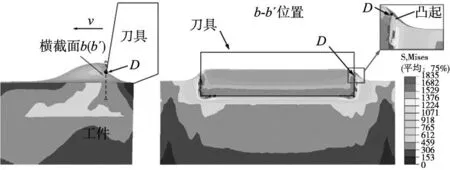
图9 毛刺变形凸起形成阶段

毛刺的形成阶段如图10所示,当刀具到达横截面c-c′处时,切削层材料与基体材料在刀具前刀面的挤压作用下发生断裂,切口边缘处的塑性变形终止,当材料拉伸超过韧性材料断裂阈值时,材料的凸起变形将发生断裂,因此,切削层材料与基体产生撕裂区域,该阶段标志着切口毛刺的完全形成,如图10右图所示。

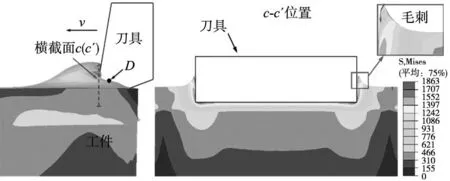
图10 毛刺完全形成阶段

D点位于工件切口边缘处未切削表面上,工件在切削工程中其D点处的应力变化如图11所示。应力变化的过程可分为3个阶段:Ⅰ弹性变形、Ⅱ屈服行为和塑性变形、Ⅲ完全塑性变形和撕裂。

图11 D点的应力值变化

通过工件材料的凸起变形仿真结果的分析及毛刺生成区域的应力分析,证明了切口毛刺的形成过程。因此在切口毛刺形成过程的基础上建立的解析模型可用于指导不同影响因素对毛刺尺寸变化规律的分析。

3.2 工艺参数对毛刺尺寸的影响规律

工艺参数是提高加工效率和加工表面质量的重要变量。因此,通过研究工艺参数对毛刺尺寸的影响规律,可抑制毛刺的产生。

图12展示了不同刀具前角(每转进给量f=0.02 mm/r和切削速度v=40 mm/s)下毛刺形状的有限元仿真结果。结果表明,其它工艺参数不变,毛刺尺寸随刀具前角的增大而减小。刀具前角减小导致切屑在离工件更远的加工表面处分离,因此,随着前角的减小,相应的毛刺尺寸将增大。图13展示了不同刀具前角下切口毛刺尺寸的变化规律,刀具前角接近0时,毛刺尺寸显著增大。由于前角越小,切削性能越差,增加了刀具前刀面处的金属阻碍。

图12 不同刀具前角下切口毛刺的等效应变云图

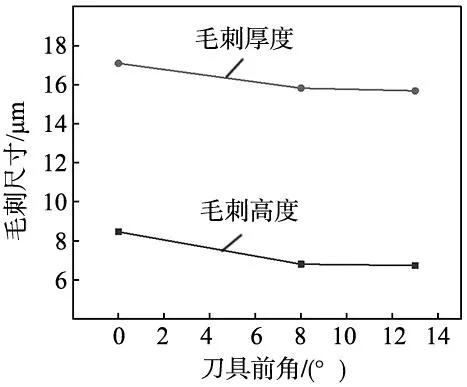
图13 刀具前角对毛刺尺寸的影响规律

图14展示了不同进给量(切削速度v=40 mm/s和前角γ=8°)下毛刺形状的有限元仿真结果。可见毛刺尺寸的趋势:毛刺尺寸随着每转进给量的增大而增大。在低进给量下切削状态比较稳定,切屑分离时工件边缘不会出现严重的撕裂现象,同时切削层厚度越小,材料流动越容易发生,毛刺尺寸也越小。然而,进给量较高时切削厚度增大,横向未变形层上的材料流动不易发生,导致切削过程中更多的材料被挤压流动到工件的顶部边缘,毛刺尺寸相应增大。

图14 不同进给量下切口毛刺的等效应变云图

图15为每转进给量对毛刺尺寸的影响规律,从曲线可以看出,随着每转进给量的增加,毛刺尺寸变化幅度显著增大。

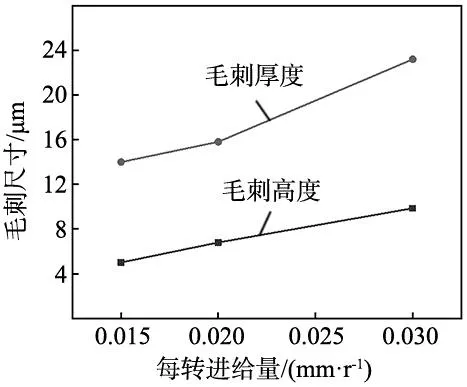
图15 每转进给量对毛刺尺寸的影响规律

图16为不同切削速度(前角γ=8°和每转进给量f=0.02 mm/r)下毛刺形状的有限元仿真结果,可以看出随着切削速度的增加,毛刺尺寸几乎未发生改变,切削速度对毛刺尺寸影响不敏感。

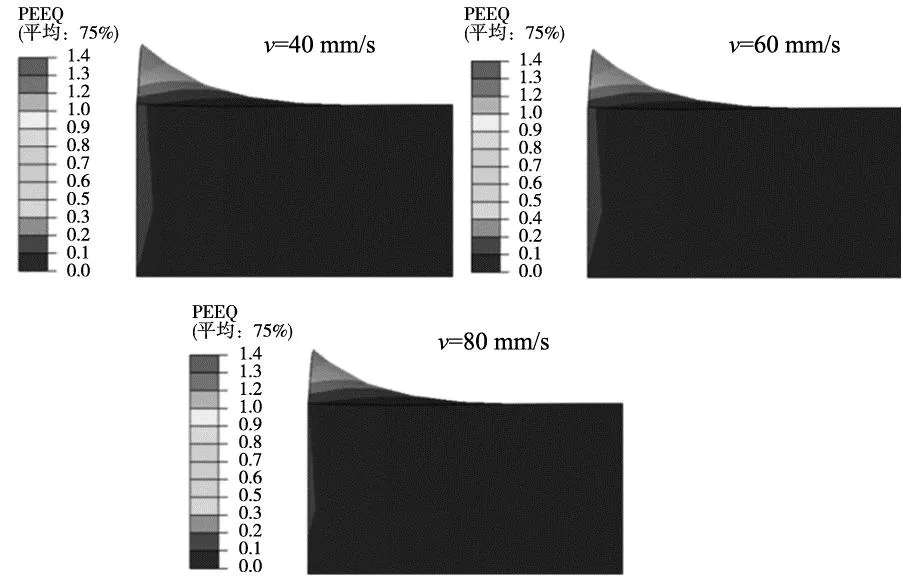
图16 不同切削速度下切口毛刺的等效应变云图

图17展示了不同切削速度对毛刺尺寸的影响规律,从曲线可以看出,随着切削速度的增大,毛刺尺寸减小,减小的趋势比较平缓。

图17 切削速度对毛刺尺寸的影响规律

4 结论

针对不锈钢管在切断过程中毛刺产生的特征,建立解析模型并得出切口毛刺的影响因素,结合三维动态切削仿真模型,模拟了毛刺的形成过程,通过有限元仿真结果与试验测量结果的对比,表明建立的仿真模型可进行预测工艺参数对切口毛刺影响规律。主要结论如下:

(1)通过建立毛刺的解析模型,解释了剪切力在切屑与工件分离时所起的作用,并得出切口毛刺形成的影响因素。

(2)利用仿真模型预测在不同工艺参数条件下毛刺尺寸的变化规律,研究结果表明,增大刀具前角、提高切削速度或者减小每转进给量,均能抑制毛刺的产生。与切削速度相比,刀具前角和每转进给量对毛刺尺寸的影响更加明显。其中,每转进给量的影响最为显著,因此在实际生产过程中,保证生产效率的前提下,可优先降低每转进给量抑制毛刺的产生。