大型数控成形磨齿机齿距误差溯源*

彭加兵,洪荣晶,刘洋河,胡 敏,丁亚凯

(南京工业大学机械与动力工程学院,南京 211899)

0 引言

大规格高精度齿轮广泛应用于船舶、风电齿轮箱、重型机械等高端装备中,直接影响机械设备的可靠性和平稳性。磨齿作为齿轮加工最后一道工序,其精度往往直接决定了齿轮的性能。大型数控成形磨齿机存在结构尺寸大,行程长、自由度多的特点,使得机床的误差项众多[1],机床的几何误差、热误差、刀具磨损误差、工件装夹误差等都会对齿距精度产生影响[2-3],因此需要通过敏感性分析方法确定出影响齿距精度较大的误差项,对其进行补偿,达到降低齿距误差的目的。

很多学者对误差的溯源和补偿做了研究。程强等[4]基于多体系理论,通过计算误差敏感度系数来识别机床的关键性几何误差。焦寿峰[5]利用基于经验模态分析法对误差模型进行分析,并对加工误差进行溯源,通过软件仿真证明了此方法的可操作性。唐宇航等[6]通过建立五坐标龙门加工中心加工误差模型,采用蒙特卡洛模拟法识别了影响加工精度的关键误差参数。LI等[7]以矩阵偏微分方程为基础,根据五轴立式加工中心敏感性分析结果对机床进行改进,提高了机床加工精度。武剑等[8]在局部灵敏度分析的基础上,结合误差贡献度判定准则实现了机床关键几何误差元素溯源。荣茂林等[9]利用Sobol全局灵敏性分析方法对机床的空间误差建模进行计算,将21项几何误差项简化成12项。黄浩等[10]基于多体系理论,构建了包含几何误差的空间位姿误差模型,采用微分矩阵敏感性分析方法得出了几何误差敏感源与配置间的映射关系,可快速对误差项进行定性判定。GUO、CHENG等[11-12]采用傅里叶幅值灵敏度检验扩展法对机床进行敏感性分析,有效识别出关键几何误差 ,从而提高了机床几何精度。阳辉等[13]通过讨论转台的回转误差、刀具磨损误差和机床热变形误差对齿距误差的影响,提出了跨齿加工的加工方法,有效地提高了齿轮齿距类误差的加工精度。

上述已有研究,分析的目标主要是刀具的空间位姿,或齿面精度,但对于齿距误差的溯源,国内还鲜有人研究。为此,本文基于多体系理论和空间啮合原理,建立机床静态误差-齿距误差的数学模型,分析机床的45项静态误差对齿距误差的映射关系,最终通过Morris全局灵敏度分析方法对机床的静态误差进行溯源,可直接辨识出对齿距精度影响最大的误差项,从而为后续的补偿提供理论基础。

1 砂轮廓形获取

1.1 齿面方程建立

由于齿距误差的评定是在渐开线上进行评价,且对于大型齿轮来说,磨齿往往是加工渐开线部分,故此本文在研究过程中仅仅分析加工渐开线的部分。

对于渐开螺旋面齿轮来说,其特点是端截面为渐开线,如图1所示。

图1 渐开螺旋面齿轮端截形

设基圆半径为rb,齿槽右侧的渐开线起点为e,oe与x轴的夹角为σ0(基圆齿槽半角),渐开线上任意一点M的法线与基圆的切点为a,取∠eoa的值u为变量,依据渐开线的性质,Ma=rbu,故渐开线ef的方程为:

(1)

将渐开线ef绕齿轮的轴线做螺旋运动,即可得到齿轮的右侧的螺旋面方程为:

(2)

根据空间啮合原理,砂轮与齿轮的接触线满足:从刀具座标系的原点Og向螺旋面上的点做径矢R,如果R和螺旋面上该点处的法线N以及刀具的轴线k′共面,则为螺旋面上的接触点。其满足的关系式为:

znx+actgγny+(a-x+Pctgγ)nx=0

(3)

式(3)为关于变量u和θ的一个关系式。

1.2 砂轮廓形方程

图2为砂轮加工斜齿轮时的接触示意图,建立工件坐标系OgXgYgZg,其中Zg轴为齿轮的轴线,Xg轴为均分齿轮齿槽的轴线,Yg轴为垂直于Xg、Yg轴的轴线;砂轮坐标系以Zw轴为砂轮回转的轴线,Yw轴与Zg轴的夹角为γ(安装角),Xw轴与Xg轴重合,但方向相反,两坐标系原点之间的距离为Da。

图2 成形磨齿坐标系示意图

使用牛顿迭代法对式(2)和式(3)进行求解,获得接触线点集。通过坐标变换将该接触线由工件坐标系转到砂轮坐标系,其变换方程为:

(4)

并通过式(5)将其绕砂轮轴线进行回转即可得到最终砂轮的廓形。

(5)

2 齿距误差评价模型

2.1 误差变换矩阵

在磨齿加工的过程中,机床的各项误差包括几何误差、砂轮磨损误差、热误差等最终都会影响砂轮与齿轮的接触线,将砂轮上的各个点投影至齿轮的端面,得到所加工齿轮的端截形。图3为在齿轮坐标系中砂轮加工齿轮时的相对位置。

图3 砂轮与齿轮的相对位置(无误差) 图4 砂轮投影与理论齿轮端截形(无误差)

图4为不考虑误差时砂轮投影的端截形和齿轮的端截形,两者完全重合。

在考虑机床的各项误差作用下砂轮的位置以及形状,采用多体系理论的方法将考虑各项误差影响下的砂轮廓形投影至齿轮坐标系中,表1为在机床加工过程中所需要考虑的各项误差,主要有:机床的几何误差、砂轮的磨损误差、转台的回转误差以及工件的安装误差等,将表中所示的各项误差转变成机床的几何误差,通过坐标变换将带有误差的砂轮廓形投影至齿轮坐标系中。

表1 机床加工过程中的误差

图5为数控磨齿机的结构示意图,机床的X、Y、Z、A、C轴各有6个自由度方向的误差,则由A轴到C轴的坐标变换矩阵为:

图5 机床结构示意图

(6)

式中:

式中:εmn表示m轴沿着n方向的角度偏转,δmn表示m轴沿着n方向的位移变化。

砂轮在加工过程中的磨损Δr可视为定值,则考虑磨损时误差变换矩阵为:

工件在安装过程中会产生偏心,将其沿着X和Y方向进行分解,其变换矩阵为:

将上述所有误差项均考虑在内,建立由刀具坐标系到工件坐标系的变换矩阵:

(7)

使用MATLAB软件对矩阵进行计算,最终可将考虑误差的砂轮廓形在齿轮坐标系中进行表示。

将该砂轮廓形投影至齿轮的端面坐标系中,得到如图6所示的实际齿面端截形和理论齿面端截形。

图6 砂轮投影与齿轮端截形(考虑误差)

2.2 单齿距误差评定

在获得砂轮投影的端面截形和齿轮理论端面截形以后,求解其与分度圆的交点,将两交点与齿轮圆心交点连线的夹角求解出,与分度圆半径相乘即可得到齿距误差。图7为齿距误差评定的示意图。

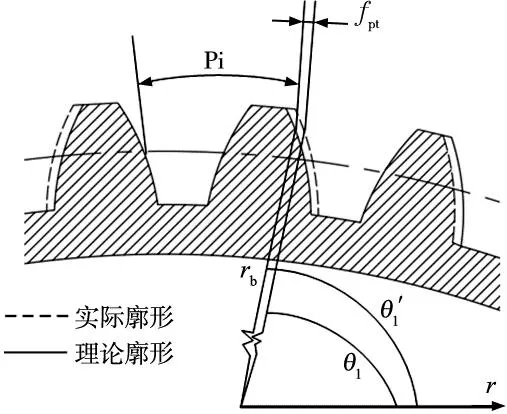
图7 齿距误差评定

3 敏感性分析

在磨齿加工过程中,会受到众多误差项的干扰,且误差项之间存在耦合效应,将众多误差项准确辨识并进行补偿是提高磨齿机加工精度经济、高效的方式。在第2节中所建立的准静态误差-齿距误差是一个多输入单输出的问题,其中,单齿距误差fpt作为该模型的输出项,表1所示的准静态误差作为模型的输入项(共45项误差),该模型可简化为:

fpt=f(G)

(8)

Morris法常用于量化计算输入参数在全局范围内对模型输出的影响程度,Morris法的实现依赖于计算单个参数的“基本效应”(elementary effect,EE),每次计算时所有输入参数中仅有某一项取值不同。在基于GE-TSEM进行敏感误差溯源时,若有xi～Fi(μi,σi),即可采用Fi分布的均值μi和标准差σi作为敏感指数来量化第i项几何误差元素xi相对于齿距误差的敏感性大小。μi值越大表明xi对齿距误差的影响越显著,σi值越大表明xi与其余误差元素之间的耦合作用越强。此外,考虑到Morris法会产生随机误差,在敏感指数的计算中,需要独立重复多次求取平均值。

在基于Morris法进行齿面敏感误差溯源分析时,需要先将每项输入误差元素的取值范围映射到区间[0,1]中,并等距离散化为{0,Δ,2Δ,…,1},每项误差元素只能在其间采样取值。其中,Δ表示采样间隔,且Δ=1/(q-1),q表示采样数。由此,可构造随机采样矩阵:

G0=(x1,x2,…,xm)T

(9)

若仅仅使误差元素xi的取值存在差异Δ,则可根据下式计算xi的“基本效应”。

基于Morris法计算敏感指数的具体过程为:

E*=(2S-E)·D*+E

(10)

步骤2:构建几何误差向量G*,取值在{0,Δ,2Δ,…,1}中随机均匀采样。

(11)

由于D*、G*、P*均为随机矩阵且相互独立,因此S*也是随机矩阵。此外,该矩阵的相邻两行之间仅有某项误差元素取值不同,若某相邻两行的第i列对应的误差元素相差Δ,可计算xi的“基本效应”为:

EEi=[f(x1,x2,x3,…,xi1,…,xm)-
f(x1,x2,x3,…,xi2,…,xm)]/Δ

(12)

步骤4:设定循环采样次数为SN,按步骤1～步骤3多次计算,可得到每项误差元素的SN个“基本效应”。

步骤5:分析每项误差元素“基本效应”的分布情况,根据式(13)计算分布的均值μi和标准差σi,记作误差元素对齿面误差的敏感指数。

(13)

步骤6:根据敏感指数比较几何误差元素的敏感性强弱,溯源得到敏感误差。

4 实例计算

在进行灵敏度分析之前,需要对误差的范围进行辨识。如图8所示,使用雷尼绍XM-60激光干涉仪对机床的X、Y、Z三个直线轴进行测量,该激光干涉仪可直接测量出直线轴6个自由度方向的误差。

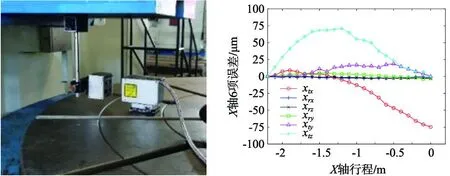
图8 精度测量 图9 X轴测量结果

图10 Y轴测量结果 图11 Z轴测量结果

测量结果如表2所示。

表2 磨齿机运动轴几何误差元素辨识

由于在加工时,砂轮的廓形由齿轮的参数以及加工条件所决定,故在进行仿真计算时,以表3所示的齿轮进行计算。

表3 齿轮参数

砂轮加工工件时与工件的位置关系为:中心距(Da)为150 mm,砂轮偏转角(γ)为70°,对于机床直线轴的几何误差可参考表3,对于A轴和C轴,可将其直线误差和角度误差视为分布在[0,20] μm和[0,20] μrad。运动轴之间的垂直度误差取值为50 μrad,砂轮的磨损误差Δr在加工单齿过程中可视为静态,取值为30 μm,齿轮在装夹过程中的偏差Δx、Δy取值为20 μm,将各个数值分别带入公式中,可获得对应误差下的齿距误差。以45项静态误差所构成的误差序列为横坐标,均值效应和标准差效应为纵坐标,绘制齿距误差的敏感指数图,其最终溯源结果如图12和图13所示。在横坐标的误差序列中,第1～6项为X轴的6项几何误差δx(X),δy(X),δz(X),εy(X),εx(X),εz(X);第7～12项为Y轴的6项几何误差δx(Y),δy(Y),δz(Y),εy(Y),εx(Y),εz(Y);第13～18项为Z轴的几何误差δx(Z),δy(Z),δz(Z),εy(Z),εx(Z),εz(Z);第19～24项为A轴的几何误差δx(A),δy(A),δz(A),εy(A),εx(A),εz(A);第25～30项为C轴的几何误差δx(C),δy(C),δz(C),εy(C),εx(C),εz(C);第31～33项为机床直线轴间的垂直度误差Syx、Szx、Syz;第34～37为C轴的安装误差δCx、δCy、αCY、βCX;第38～41项为A轴的安装误差δAY、δAZ、βAZ、γAY;第42项为砂轮磨损误差Δr;第43～44项为工件的安装误差Δx、Δy;第45项为转台回转误差Δθ,最终溯源结果如图12和图13所示。

图12 误差的均值效应 图13 误差的标准差效应

由图12的结果可得出结论:转台的回转角度误差Δθ对于齿距误差的影响因素最大,达到了0.097,在实际加工中,也确实如此,因为齿距误差直接受到转台回转精度的影响,其次是C轴沿着Z方向的偏摆,为0.089。对45项误差的敏感指数进行排序,将前7位误差项列出:Δθ>εz(C)>βa(Z)>εz(X)>Sy(X)>εy(X)>εy(A)。

由图13可得出结论:Szx与其他误差项的耦合作用最明显,其余误差项中,敏感指数较大的前7项为:Sz(X)>εz(X)>Δθ>εy(Y)>εx(A)>εx(Y)>εz(C)。

5 结论

通过建立机床静态误差-齿距误差的多输入单输出的误差模型,使用Morris敏感性分析算法,对45项机床静态误差进行分析,获得了各个误差项的敏感指数。所得结论如下:

(1)偏转误差为主要误差源,对齿距精度具有显著影响,而直线误差的敏感系数均较小。

(2)转台的回转误差在所有的误差项中个体效应最明显,对齿距精度的影响最大。

(3)各运动轴的偏转误差以及垂直度误差与其他误差的耦合效应较为明显,在后续的补偿中,需要对其进行解耦分析。

(4)利用本文的误差溯源模型及算法,可较快地获得影响齿距精度的误差项,对于生产实践具有一定的指导意义。