直线电机高速高精运动分段式三元复合控制*

汪惟桢,张 驰,李 荣,桑 娜,潘春荣,郑林卫

(1.江西理工大学机电工程学院,赣州 341000;2.中国科学院宁波材料技术与工程研究所浙江省机器人与智能制造装备技术重点实验室,宁波 315201;3.宁波尚进自动化科技有限公司,宁波 315100)

0 引言

半导体引线键合机作为芯片封装制造的关键设备,主体是一个由永磁同步直线电机组成的XY运动平台。直线电机具有响应速度快、定位精度高等优点,但由于取消了传动环节和系统低阻尼特性,外部扰动将直接作用于电机[1]。此外,非线性滚珠轴承引入的柔性模态也会影响其控制性能[2]。引线键合工艺是短行程的高速点对点运动,因此,直线电机在有限的行程内需要更高的加速度。随着集成电路产业的发展,对键合机生产效率和精度的要求不断提高。因此,如何在高速高精运动条件下实现快速准确的定位是提高键合机性能的关键。

仅有反馈环节的控制器会带来不可避免的滞后效应,通过引入前馈控制器可极大地降低动态误差。目前常用的前馈控制器是基于模型逆的经典前馈控制方式[3-4]。反馈和前馈组成的复合控制方法可实现直线电机的高速高精运动[5],但高加速度引起的残余振动严重影响了系统定位精度。增加物理阻尼[6]或设计隔振装置[7]是减小直线电机残余振动的直接方法,但附加的机械结构增加了成本。通过离线设计平滑的轨迹同样可以有效降低运动过程中和运动结束阶段的振动[8]。在指定运动轨迹下,通过设计智能控制器,如迭代学习控制(ILC)[9]、神经网络[10]等,可有效减少振动。但迭代学习对输入轨迹的变化敏感,智能控制算法需要较长的调试时间。扰动观测器(DOB)被广泛应用于实时抑制集总扰动,若将残余振动也视为集总扰动的一种,则DOB可以有效降低残余振动带来的误差[11]。然而,过去DOB中低通滤波器的带宽一般低于直线电机的谐振频率[12-13],主要被应用于低频运动中的扰动抑制。

本文提出一种分段式三元复合控制方法,分别对高速运动阶段和定位阶段设计不同的控制结构。首先,通过对直线电机进行正弦扫频,辨识其高阶精确模型;然后,设计三阶前馈控制与PID反馈控制组成的复合控制系统,实现直线电机的高速高精运动;最后,在定位阶段引入高阶扰动观测器,抑制直线电机在高加速度运动结束后的残余振动。实验结果表明,在不影响动态性能的前提下,所提出的控制方法有效提高了键合机X轴直线电机定位精度。

1 永磁同步直线电机动力学建模

永磁同步直线电机伺服系统具有各部件耦合复杂、参数测量难度大和不精确等特点,基于数学理论建立的名义模型与真实模型误差较大[14]。本文研究的键合机X-Y运动平台如图1所示,其Y轴叠加于X轴上,因此X轴的负载较大,在高速启停时易产生残余振动。

图1 被控对象平台

为实现高速高精运动,需要设计高带宽的伺服控制器,因此,如何在高频段进行精确建模尤为重要。本文对X轴直线电机进行正弦扫频后,将位置传感器采集的数据进行差分处理,并对输入输出信号进行快速傅里叶变换(FFT),拟合得到频域特性曲线,建立直线电机的高阶精确模型[14]。

对X轴直线电机的5个不同位置进行正弦扫频,其中,输入信号的频率范围为20 Hz～2000 Hz,采样频率为16 000 Hz。曲线拟合结果如图2所示,其中灰色实线为FFT得到的辨识结果,黑色虚线为拟合的直线电机名义模型。由图2可知,拟合得到名义模型与实际模型的频率响应特性接近。

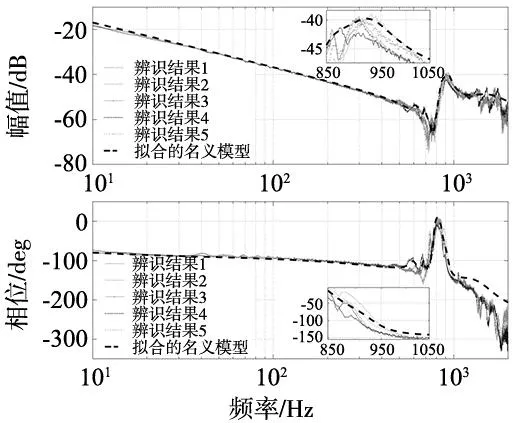
图2 X轴直线电机多点扫频与模型拟合

经过MATLAB处理后,拟合的X轴直线电机的动力学名义模型为12阶模型,其传递函数表达式为:

(1)

GX1(s)=-21.0868s11-1.7286×104s10-2.0929×109s9+
7.6279×1012s8-6.4832×1016s7+7.3323×1020s6-
5.4395×1023s5+2.3584×1028s4+5.5842×1030s3+
3.2032×1035s2+7.8201×1019s+1.5668×1042

(2)

GX2(s)=s12+1.3628×104s11+2.4239×108s10+2.1227×1012s9+
1.7903×1016s8+1.196×10s20+5.7271×1023s6+
3.111×1027s5+8.2905×1030s4+3.7728×1034s3+
4.4585×1037s2+1.7149×1041s+2.0978×1042

(3)

该传递函数能较准确地描述被控对象在高频段的柔性模态,为控制器的设计和仿真奠定基础。

2 控制方案设计

针对键合机X-Y运动平台的X轴直线电机,提出了一种分段式三元复合运动控制方法。该方法通过判断直线电机的运动速度指令是否为0,区分电机的运动阶段和定位阶段。当速度指令不为0时,为运动阶段;当速度指令为0时,为定位阶段。在运动阶段进行“前馈+反馈”的复合控制,实现高动态响应;在定位阶段进行“反馈+扰动观测器”的复合控制,实现高定位精度,控制框图如图3所示。

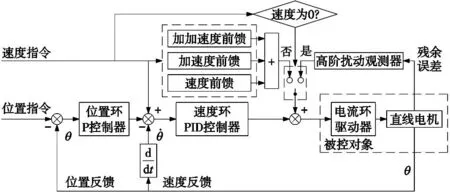
图3 分段式三元复合控制方法

2.1 “前馈+反馈”复合控制方法

由于电流环已在商业驱动器中实现,基于经典的三环控制理论,对闭环反馈控制系统的速度环和位置环进行设计。本文中,速度环和位置环分别设置为P控制器和PID控制器。反馈控制器在系统产生跟踪误差后输出控制信号,存在固有的滞后效应。随着跟踪误差的减小,在恒定增益下的反馈控制作用减弱,难以进一步提高跟踪精度。此外,键合机高速运动时,反馈控制器的滞后效应更明显,带来较大的动态误差。

为实现直线电机高速高精运动的快速跟踪,前馈控制器提供大部分控制电流。且由经典控制理论可知,前馈控制器不影响原闭环反馈系统的稳定性[4]。因此,在反馈控制系统中引入前馈控制器,从而提高动态性能,组成的复合控制框架如图4所示。

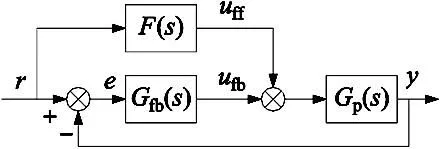
图4 复合控制框架原理图

图4中,r为位置参考轨迹,F(s)为前馈控制器,Gfb(s)为反馈控制器,Gp(s)为被控对象。忽略各种扰动,且被控对象的名义模型是可逆的,则跟踪误差e可以表达为:

(4)

由式(4)可知,当满足条件:

(5)

时,即前馈控制器F(s)为被控对象的逆模型时,可实现对参考轨迹的零误差跟踪。被控对象从电流输入U(s)至位置输出Y(s)的传递函数一般表达为:

(6)

式中:分母的阶数高于分子,因此Gp(s)的反演可以展开为s=0时的泰勒级数:

(7)

由于被控对象至少为一阶无静差系统,可知c0=0[15]。式(7)表明,前馈控制器为位置输入信号的1阶至k阶微分形式。本文设计的三阶前馈控制器由速度前馈、加速度前馈和加加速度前馈组成:

F(s)=Kvs+Kas2+Kjs3

(8)

此时,F(s)并不完全等价于被控对象的逆模型,但可作为其降阶近似[16]。式(8)的输入为位置参考信号,若改为速度信号V(s),则前馈控制器对应的二阶速度名义模型的传递函数为:

(9)

基于图2的辨识结果对二阶速度名义模型进行拟合,得出的三阶前馈控制器参数为:

(10)

2.2 高阶扰动观测器

在高速运动中,高频输入信号将激发直线电机被控对象的柔性模态,产生的残余振动影响定位精度。且在直线电机定位阶段中,即输入轨迹结束后,前馈控制器不再输出控制信号,仅存的反馈控制器难以保证高定位精度。本文引入扰动观测器(DOB)观测并抑制运动结束后的残余振动,其基本结构如图5所示。

图5 扰动观测器的基本结构

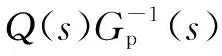
由图5可知,系统的灵敏度传递函数SDOB和补灵敏度函数TDOB:

(11)

(12)

当系统模型足够精确,即W(s)=0时,有:

SDOB=1-Q(s)

(13)

TDOB=Q(s)

(14)

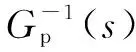
(15)

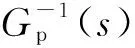
图6 带宽为1000 Hz的巴特沃斯低通滤波器伯德图

在低通滤波器的截止频率附近,扰动估计值dest相比实际输入扰动d存在幅值衰减和相位滞后,故扰动观测器的补偿精度将随扰动频率的增加而降低。在高速运动下,控制器的输出电流信号包含高频分量,导致扰动观测器在直线电机运动过程中的补偿效果降低,影响动态跟踪精度。因此,通过采用分段控制的方式,即在定位阶段,指令速度为0时,引入高阶扰动观测器,避免影响系统动态精度。

3 实验验证

3.1 实验平台搭建

实验平台搭建如图7所示。X-Y运动平台的X轴直线电机由AMC SX25A20型模拟伺服驱动器驱动。电机的位置信息由雷尼绍光栅尺测量并反馈至Power PMAC控制器。参考轨迹和控制算法在设计完成后通过编程写入Power PMAC IDE,经过编译后由以太网下载至Power PMAC控制器中,实现对直线电机的点位运动控制。系统控制频率为16 000 Hz,光栅尺精度为50 nm。

图7 实验平台搭建

3.2 实验结果

以键合机X轴直线电机为被控对象,验证所设计的分段式三元复合控制方法的性能。输入信号为三阶S型点位运动轨迹,位移为4 mm,最高速度0.58 m/s,最高加速度为160 m/s2,如图8所示。

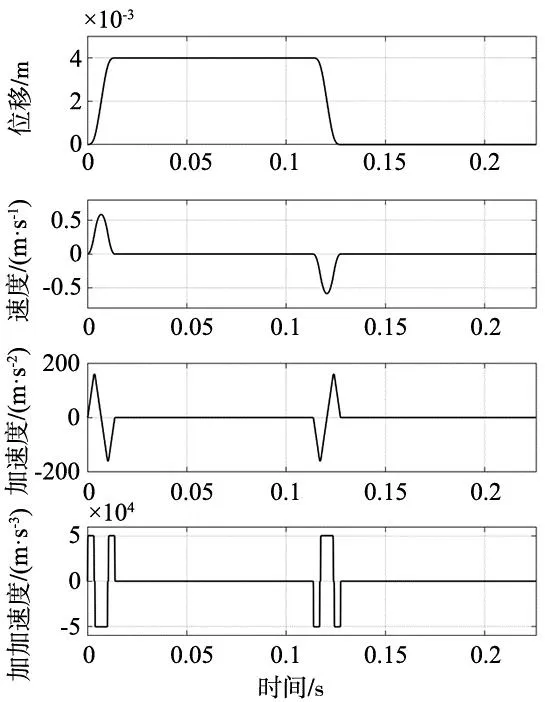
图8 三阶S型点位运动轨迹

直线电机系统在传统的“前馈+反馈”复合控制和分段式三元复合控制下进行轨迹跟踪实验,对应的轨迹跟踪误差和定位误差分别如图9和图10所示,两种控制方法的性能对比如表1所示。

表1 传统复合控制与分段式三元复合控制的性能对比

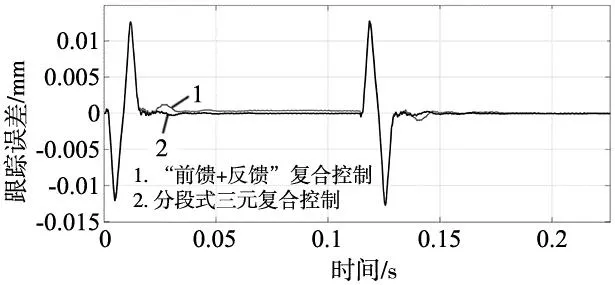
图9 分段式三元复合控制效果

实验结果表明,使用传统的“前馈+反馈”复合控制方法时,直线电机的残余振动和摩擦力对定位精度的影响较大,导致电机在下一阶段无法从初始位置开始运动。使用分段式三元复合控制方法时,各阶段定位误差调整至±0.5 μm所需的时间分别降低了89.47%和89.21%,且最大跟踪误差的变化仅为0.07 μm。因此,本文提出的分段式三元复合控制方法能有效降低残余振动带来的定位误差,且对动态跟踪精度的影响很小。

将HODOB应用于整个点位运动时,尽管可以改善定位误差,但最大动态跟踪误差由12.68 μm增大至16.61 μm,如图11所示。

图11 HODOB对动态精度的影响

从图11可以看出,在高速运动阶段,扰动观测器将影响直线电机的动态跟踪精度,证明了分段控制的必要性。

4 结论

针对直线电机在高速高精运动中残余振动较大,导致键合机X-Y运动平台定位精度降低的问题,本文设计了一种分段式三元复合运动控制方法。通过“前馈+反馈”的复合控制方法实现了高动态响应;基于正弦扫频辨识得到的高阶精确模型,建立了高阶扰动观测器,并设计相应的高带宽低通滤波器,对运动结束阶段的残余振动和摩擦等扰动进行观测并抑制,提高了定位精度。半导体键合机的X轴直线电机在进行最高速度0.58 m/s,最高加速度160 m/s2,行程为4 mm的点位运动时,使用分段式三元复合控制方法实现了最大跟踪误差为12.75 μm的动态跟踪精度,与“前馈+反馈”的复合控制方法相比,调整时间缩短了89%以上。因此,本文提出的分段式三元复合控制方法在保证系统高定位精度的同时,兼顾了高动态精度,满足了自动化设备高速高精运动的需求。