基于时间-冲击最优的机械臂喷涂轨迹优化*
周程胜,熊瑞平,胡英达,李 静,巫启源
(四川大学机械工程学院,成都 610065)
0 引言
在产品制造过程中,涂装是一个重要的处理过程,具有为产品提供涂层保护,以及提高产品的美观性等优点[1]。由于喷涂过程中会产生大量醛、苯等有毒气体,长期在该环境下工作会对操作人员的身心健康产生危害,所以随着机器人等先进制造技术的发展,机器人喷涂逐渐取代人工喷涂的方式[2]。喷涂质量和工作效率是衡量机械臂喷涂路径优劣的关键指标,因此,需要对喷涂机械臂进行工作轨迹优化,以提高喷涂作业效率、降低运行过程中产生的冲击振动从而提高喷涂质量。
多项式插值因为其计算简单的特点被广泛应用于机械臂轨迹规划,但是三次多项式曲线会产生加速度突变[3],插值次数太高往往会出现龙格现象,并且多项式插值不具有局部可控性[4],一两个路径点的变动就会引起整条曲线轨迹的改变,无法满足机械臂在动态环境中工作的适应性。因此具有局部修改性的B样条插值曲线引起了国内外学者的关注,李小霞等[5]基于5次B样条构造了加加速度连续光滑的关节空间轨迹,解决了关节平滑驱动的问题,但未涉及智能优化算法。GASPARETTO等[6]在5次B样条插值轨迹的基础上运用权重法将时间-冲击最优问题转化为单目标问题利用SQP方法(序列二次规划)获得最优轨迹。权重法有效降低了算法求解难度,同时该方法弱化了优化目标之间的关联性,因此牺牲了部分性能指标。
本文在关节空间中利用五次非均匀B样条函数构建插值轨迹,以机械臂运行时间和冲击为目标建立多目标优化数学模型,结合改进的多目标灰狼算法进行多目标优化。以曲面工件喷涂作业仿真为例进行算法求解并获得Pareto最优解集并将优化结果与NSGA-Ⅱ算法[7]优化结果进行性能比较。最后构造归一化权重目标函数以获得最优解并规划出时间-冲击最优的关节喷涂轨迹。
1 最优喷涂轨迹规划问题描述
关节空间喷涂轨迹规划的首要任务就是将笛卡尔空间中的喷涂轨迹离散化,通过机械臂逆运动学转换为关节空间的关键路径点的关节序列来构造过关键喷涂路径点且连续光滑的基本轨迹曲线。
喷涂工作效率和喷涂质量是最优喷涂轨迹规划中需要优化的目标,因此机械臂最优喷涂路径规划问题可以定义为多目标优化问题,其数学模型可表示为:
(1)
式中:目标函数Si(x)(i=1,2,…,f)及约束函数gi(x)≤0和hk(x)=0都是决策变量x=(x1,x2,…,xn)的函数。
为了提高机械臂喷涂效率,同时通过减小冲击所带来的关节振动以改善喷涂质量,可将优化目标定义为:
(2)
(3)
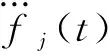
(4)

2 基于B样条插值的轨迹构造
2.1 B样条曲线描述
K次B样条曲线的定义为:
(5)
式中:Qi(i=0,1,…,n)为控制顶点,Ni,k(u)(i=0,1,…,n)是k次规范B样条基函数,其节点矢量U=[u0,u1,…,un+k+1]。Ni,k(u)(i=0,1,…,n)可由德布尔-考克斯递推公式定义:
(6)
式中:k表示B样条函数的次数,i表示B样条曲线的序号。由递推式可知:
(1)Ni,k(u)只在节点区间[ui,ui+k+1]中不等于0,在其它节点区间均为0,即B样条曲线具有局部支撑性;
(2)在任一确定的区间[ui,ui+1]之间,存在不超过k+1个非0的Nj,k。
因此B样条曲线可简化为:
(7)
2.2 5次非均匀B样条插值轨迹
为获得加加速度连续且光滑的轨迹,利用5次B样条函数构造插值曲线。为使每个关节机械臂轨迹经过给定的n+1个位置点,需反求B样条插值轨迹方程的n+k个控制点Qi(i=0,1,…,n+k-1)。
B样条曲线由控制点Qi和节点矢量U=[u0,u1,…,un+2k]定义。为保证B样条曲线始末端点和始末位置点重合,取节点矢量两边的重合度为k+1即:u0=u1=…uk=0,un+k=un+k+1=…un+2k=1。内节点值可采用累计弦长参数化法[8]对时间节点Δti归一化得到:
(8)
将时间-位置序列M={(pi,Δti)|i=0,1,…,n}代入式(7)可得到满足插值条件的n+1个方程。因此还需要增加k-1个条件,本文取k=5,通过设定关节始末速度和加速度可获得剩余4个边界条件:
(9)
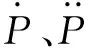
(10)
通过解n+k个线性方程组,可以求解出的控制顶点向量Qj,由控制顶点Qj,时间节点矢量U可得到关节j在t∈[t0,tn]上的轨迹曲线方程,再通过式(11)就能推导出其各阶导数曲线,即:
(11)
3 运动约束问题处理
因为B样条曲线具有强凸包性质[9],整条曲线包含在控制多边形的凸包内。因此可以将运动约束条件转化为每个关节的各阶B样条插值曲线控制顶点的约束,简化约束条件。
(12)
对于一个解x,若其满足约束条件,则称该解为可行解,若不满足,则称为不可行解。对于不可行解,一般使用约束违反值[10]来描述其违反约束的程度:
(13)
式中:gi(x)表示不等式约束,hk(x)表示等式约束。其中〈α〉表示若α≤0,则〈α〉=0,否则〈α〉=|α|,显然,对于一个解,其CV值越小,说明该解越优。
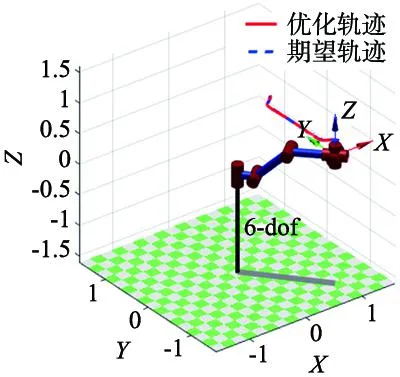
对于任意两个解xa约束支配xb的条件满足以下条件的任一项即可:①xa是可行解,而xb是不可行解;②xa和xb都是不可行解,但是CV(xa) 灰狼优化算法(grey wolf optimizer,GWO)[11]是受灰狼群的捕食行为启发的一种生物智能算法,其具有参数少、易实现、稳定性强等优点,在处理路径规划优化问题时表现出了良好的性能。GWO算法模拟灰狼的等级制度和群体狩猎行为,每个狼群都有严格的等级制度,狼群中适应度最好3个个体为α、β和δ狼,其余个体ω狼。在GWO算法,α、β和δ狼领导狩猎行为,ω狼负责跟随这3头狼搜索最优解。 除等级制度外,为模拟灰狼的狩猎行为,通过以下公式更新灰狼位置。首先确定灰狼与猎物之间的距离: D=|C·Xp(t)-X(t)|,C=2r1 (14) 式中:Xp(t)为猎物位置,X(t)为灰狼位置,C为摆动因子,r1为[0,1]之间的随机数。 之后灰狼根据自己与猎物之间的距离更新自身的位置: (15) 式中:A为收敛系数,r2为[0,1]之间的随机数,a为从2线性递减至0的常数。 为了捕捉到猎物,由α、β和δ狼的领导来实现对猎物的锁定和围捕,其数学模型可描述为: (16) X(t+1)=(X1+X2+X3)/3 (17) 为了使灰狼算法能够用于多目标优化问题中,MIRJALILI等[12]提出了多目标灰狼算法(MOGWO),即在GWO基础上增加两个组件。 (1)利用外部存档维护迄今为止搜索到的Pareto最优解,若存档已满,则利用网格机制删除最拥挤分段中的解,以改善帕累托最优前沿的多样性。 (2)引入领导选择策略从存档最不拥挤分段中选择α、β和δ解来领导个体的位置更新。 MOGWO算法随机生成初始种群的方式遍历性低,初始解在解空间分布不均匀,从而导致算法在解空间中寻优不彻底,影响算法的搜索效率和全局寻优性能。混沌映射具有随机性、均匀性和多样性等特点,有利于生成遍布整个解空间的初始种群。本文引用Cubic混沌映射[13]实现狼群位置分布的初始化操作,其映射函数如式(18)所示。 y(i+1)=4y(i)3-3y(i) (18) 式中:y(i)为立方序列,按式(19)映射到灰狼个体上: X(i)=lb+(ub-lb)×(y(i)+1)/2 (19) 式中:ub、lb为搜索空间的上界和下界。 MOGWO算法在进行多目标优化时存在易陷入局部最优和后期收敛速度慢的问题。由式(15)可知,当|A|<1时,狼群远离头狼进行全局搜索;当|A|>1时,头狼领导狼群进行局部寻优。而线性递减的收敛因子a无法平衡算法全局和局部搜索能力,因此提出了一种非线性收敛因子如式(20)所示。 a=1+sin(π/2+pi×(t/T)1.5) (20) 如图1所示,式(20)改进后的收敛因子在迭代前期和后期衰减缓慢,中期搜索效率提高,可以更好地协调算法的全局搜索能力与局部寻优能力。 图1 改进收敛因子和原收敛因子曲线图 改进的多目标灰狼优化(IMOGWO)算法流程为: 步骤1:利用混沌映射初始化灰狼种群Xi(i=1,2,…,n),利用式(20)初始a、A、C; 步骤2:计算每个个体的适应度值,选择Pareto解并存入archive档案中; 步骤3:在archive档案中,采用领导选择策略选择α、β和δ狼t=1; 步骤4:进入迭代过程,t 步骤5:根据式(16)、式(17)更新ω狼位置,更新a、A、C; 步骤6:计算每个个体的适应度值,找到Pareto解并存入archive档案中,若存档已满则采用网格机制删除最拥挤解; 步骤7:在archive档案中,重新选择α、β和δ狼; 步骤8:t=t+1,跳转到步骤4; 步骤9:算法结束,输出Pareto解集。 本文以KUKA KR_16型工业机器人为仿真对象,进行喷涂作业仿真,其改进D-H参数如表1所示,喷涂工件及选取喷涂路径点如图2所示。 表1 改进D-H参数表 图2 喷涂工件及选取路径点 喷涂路径点的关节序列如表2所示。各个关节运动学约束如表3所示。 表2 路径点关节序列 表3 运动约束 利用非均匀5次B样条插值曲线规划喷涂轨迹,设定所有关节的启停速度、加速度均为0。根据式(2)、式(3),以S1和S2为优化目标函数,在MATLAB环境中对建立的多目标模型按IMOGWO算法流程进行求解。设置最大迭代次数为100,种群大小为100,archive档案大小为100,设置目标函数空间的每一维度的网格数为nGrid=10。为形成对比,同时采用NSGA-Ⅱ算法优化求解。得到运动时间和冲击综合优化的Pareto前沿面如图3所示。 图3 Pareto前沿面对比图 由图3中IWOGWO的Pareto前沿可知,Pareto前沿为决策者提供了许多优化解决方案,每一个Pareto解都不能在一个目标上进一步改进,而不会导致另一个目标的退化;时间性能指标和冲击性能指标呈负相关,越靠近A点,机械臂喷涂效率越高,越靠近B点机械臂运动更加平稳,喷涂质量越好;对比NSGA-Ⅱ的Pareto前沿可知,由于采用了非线性收敛因子,IMOGWO算法得到的Pareto前沿分布跨度更大,为决策者提供了更丰富的最优解方案;头狼领导的狩猎策略可以局部搜索到更加精确的最优解,使其更接近于真实Pareto前沿。 为了能在Pareto前沿面选择实际工况下的一个解,定义如下归一权重函数: fc=α1S1/N1+α2S2/N2 (21) 式中:N1和N2可以使各目标函数处于同一数值范围,α1和α2是各个目标函数根据实际工况需求所占权重比例。对式(21)最小化求解,即可从Pareto前沿面中选择最优解。 本文取α1=0.7,α2=0.3,N1=1,N2=1.5,求解获得IMOGWO算法的Pareto最优解在图3中表示为C点,最优时间序列为Δt=[3.40,1.74,1.87,1.56,1.74,1.70,3.29],最优运行时间为15.30 s,最优绝对平均冲击值为22.37 °/s3。对比NSGA-Ⅱ算法的Pareto前沿面可知:机械臂按最优运行时间序列进行喷涂作业,其冲击减小了17.6%,其喷涂效率提升了3.0%。 利用正运动学,将关节空间的最优轨迹映射到笛卡尔空间,得到如图4所示的优化轨迹。可以看出,利用本文方法对采样点进行优化后轨迹,与根据实际喷涂作业的需求所期望的喷涂路径具有良好的拟合性。验证了该轨迹规划方法的在笛卡尔空间进行喷涂作业的可行性。 图4 笛卡尔空间喷涂轨迹 各个关节的位置、速度、加速度和冲击曲线如图5所示。 (a) 各关节位置曲线 (b) 各关节速度曲线 由图5可见,采用5次B样条插值方法在关节空间中构造的轨迹,可以指定初末速度和加速度并保证冲击的连续性。通过IMOGWO对关节运动时间和冲击优化后,所有关节均满足运动约束条件的同时,各性能指标都达到了综合最优的状态,在提高喷涂效率的同时,保证了喷涂质量。 利用非均匀5次B样条插值曲线在关节空间规划的喷涂轨迹光滑连续且无冲击突变;该轨迹可指定初末速度和加速度,避免了机械臂启停时产生刚性振动与冲击;采用约束违反值将运动约束条件转换为Pareto支配关系;提出了改进的多目标灰狼算法,采用该算法获得的Pareto解集分布跨度能大且更接近真实的Pareto前沿。仿真实验的结果表明,该方法在提高机械臂喷涂效率的同时,减小了关节运动过程中冲击的累积,提高了喷涂质量。验证了基于改进多目标灰狼算法的机械臂最优时间-冲击喷涂轨迹规划的有效性。4 改进的多目标灰狼算法(IMOGWO)
-1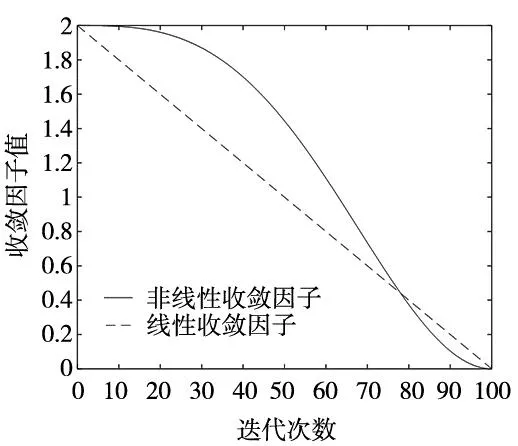
5 仿真验证



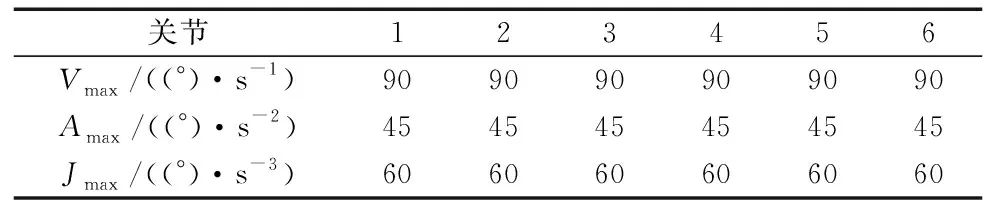


6 结论

