基于n阶S形曲线的SCARA多目标运动规划*

吴 坤,王明威,周 康

(1.郑州工商学院工学院,郑州 454000;2.郑州大学机械与动力工程学院,郑州 450001)

0 引言

SCARA是现代工业中广泛应用的一种机器人,其具有结构紧凑、高速度、高精度等优势,在电子制造业中被广泛应用,如电子元件的组装、集成电路封装等[1-2]。振动是影响电子制造产业SCARA机器人性能的主要因素,会降低定位精度、增加定位时间,从而直接导致所制造产品的质量下降和成本增加[3]。因此对SCARA机器人振动抑制的研究,是提高SCARA机器人效率和定位精度的一个重要课题。

运动规划是减小SCARA机器人振动的有效方法。目前,SCARA机器人运动规划研究多以基于D-H参数法的运动学分析为基础,然后结合MATLAB Robotics和MATLAB/SimMechanics等工具箱进行运动轨迹的规划[4-10]。这一类研究多基于刚体模型,仅通过运动学分析对其运动轨迹曲线进行规划设计,能够在一定程度上改善SCARA机器人振动特性,但是更深层次的振动抑制还需要考虑关节的柔性,从力学原理着手展开研究。

柔性多体系统动力学是机器人动力学建模的理论基础[11-13],从动力学模型所采用的广义坐标来分,柔性多体系统动力学最常用的两种表示方法是绝对节点坐标法[14]和浮动坐标法[15]。其中绝对节点坐标法对构件的大变形具有更好的模拟精度,且具有常数质量矩阵和不含科氏力等应用优势,但是其广义坐标数量较多,形成的系统方程组模型较大,需要花费大量的求解时间。浮动坐标法对构件的小变形具有很好的表达能力,且使用的广义坐标数量较少,能够节省求解时间。对于高速轻载的SCARA机器人而言,浮动坐标法具有更好的适用性。

高阶多项式曲线在运动规划中具有冲击小、过渡平滑等优点,能够有效减小机械设备在运动过程中的振动。林俊享等[16]提出了一种用于运动平台运动规划的n阶S形曲线构造方法,本文基于该方法对SCARA机器人进行振动抑制运动规划。首先,基于浮动坐标法建立了考虑关节柔性的SCARA机器人动力学模型;然后,以n阶S形曲线为基础,建立了SCARA机器人抑振运动规划问题的多目标优化模型;最后,采用基于Kriging模型的NSGA-Ⅱ算法对多目标优化模型进行求解,得到更符合工程应用需求的运动规划方案。本文从动力学分析、运动规划模型、优化模型快速求解等方面建立了SCARA机器人振动抑制运动规划的方法体系,为SCARA机器人的进一步优化设计奠定了理论基础。

1 SCARA机器人简化浮动坐标法模型

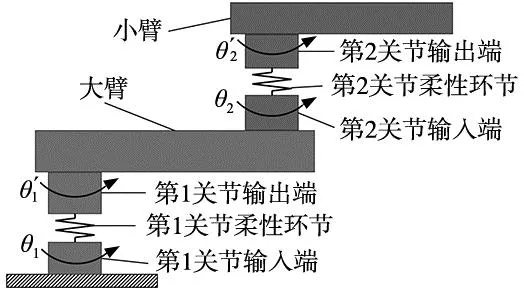
图1 SCARA机器人原理模型

(1)

为更精确地对关节变形量进行分析,根据浮动坐标法原理取θ1、Δ1、θ2、Δ2为SCARA机器人的广义坐标,记广义坐标向量为:

q=[q1q2q3q4]T=[θ1Δ1θ1Δ1]T

(2)

SCARA机器人的平面简化模型如图2所示,图中o-x-y为惯性坐标系,ci,(i=1～4)各输入、输出端的质心,ci-xi-yi为对应的连体坐标系。设mi和Ji分别为对应部分的质量和关于质心的转动惯量,ri为ci的位置矢量,其中r1为固定值。设大、小臂的臂长分别为L1和L2,其质心到对应根关节中心的距离分别为h1和h2,由几何关系可以求出其他几个质心的位置矢量为:

图2 SCARA机器人平面简化模型

(3)

(4)

(5)

另外,小臂末端的位置矢量为:

(6)

对位置矢量求导可得质心的速度矢量,将其组装得:

(7)

式中:

(8)

式中:

si=sin(θi+Δi)
ci=cos(θi+Δi) (i=1,2)

(9)

基于上述运动学分析,设两个关节的柔性环节的刚度分别为k1和k2,qi上作用的力矩为Qi,则由拉格朗日方程可得系统的动力学方程为:

(10)

式中:

(11)

(12)

(13)

Q=[Q1Q2Q3Q4]T

(14)

式(11)和式(12)中:

(15)

(16)

式中:

(17)

2 抑振运动规划

2.1 n阶S形曲线构造

工程上常用二阶S形曲线和三阶S形曲线进行运动规划,分别能够获得连续的速度和加速度。为得到更好的光滑性,林俊享等[16]提出一种n阶S形曲线的构造方法,现将其构造过程简述为:

一条完整的n阶S形曲线包含ns=2n-1个分段,每个分段都可以表达为n阶多项式Si(t),(i=1,2,…,ns),其表达式为:

Si(t)=ai,0+ai,1t+ai,2t2+ai,3t3+…+ai,ntn

(18)

式子:ai,0,ai,1,ai,2,…,ai,n表示第i段曲线表达式的待定系数,t为时间。n阶S形曲线将运动的时间区间划分为ns个分段,因此有ns+1=2n个时间节点,记为ti,(i=0,1,…,ns),则时间区间[ti-1,ti],(i=1,2,…,ns)即为第i段n阶S形曲线所对应的分段,区间长度记为Δti=ti-ti-1。

第i段曲线表达式Si(t)及各阶导数的表达式为:

(19)

n阶S形曲线为2n-1段为n次多项式的表达式,每一分段表达式包含n+1个待定系数,总待定系数个数为:

nv=(2n-1)(n+1)

(20)

因此需要构造nv个方程用于确定nv个待定系数。方程的构造方法为:

(1)初始条件。n阶S形曲线在t0时刻0～n-1阶导数均为0,共计n个方程,即:

(21)

(2)终止条件。n阶S形曲线在tn时刻函数值为确定的行程s,第1～第n-1阶导数为0,共计n个方程,即:

(22)

(3)连续性条件。n阶S形曲线的0阶导～(n-1)阶导在每个中间时间节点处应当是连续的,共计(2n-2)×n个方程,即:

(23)

(4)特殊条件。n阶S形曲线的2阶导～n阶导需要满足的特殊约束条件,在某些曲线段恒等于0,而这些曲线段的索引存在一定的规律。可以通过二阶S形曲线、三阶S形曲线和四阶S形曲线中2阶导～n阶导恒等于0的曲线段索引的规律进行归纳,得到n阶S形曲线应满足的特殊条件为:

(24)

上述4类条件得到的总方程数为:

n+n+(2n-2)×n+2n-n-1=(2n-1)(n+1)

(25)

与待定系数个数相同,因此联立以上各方程,即可求得各分段的待定系数xi。

由上述构造过程可知,n阶S形曲线的参数包括行程s和时间节点ti,(i=1,2,…,ns)。为便于确定参数的取值范围,使用时间区间长度参数Δti代替时间节点参数ti,n阶S形曲线可以记为:

S(t)=Sn(t,s,ΔT)

(26)

式中:ΔT=[Δt1Δt2… Δtns]。

2.2 运动规划数学模型

在第1节的动力学模型中,θ1和θ2为驱动自由度,设SCARA机器人的末端目标位置为rt,则根据式(6),由re=rt可求得θ1和θ2的目标值,记为s1、s2。因此,SCARA抑振运动规划可简单表述为:已知SCARA机器人末端的目标位置rt和对应的关节位移目标值s1、s3,寻找合适的运动规划曲线θ1(t)、θ2(t),使得SCARA获得最佳的工作性能。同时考虑SCARA机器人的末端定位时间和受到的冲击,采用四阶S形曲线对θ1(t)和θ2(t)进行运动规划,构造如下抑振运动规划问题的多目标优化模型:

(1)设计变量。取θ1(t)和θ2(t)的时间区间参数ΔT1、ΔT3为设计变量,对于四阶S形曲线,ΔT1和ΔT3中各包含了15个分量,对应的关节运动规划为:

θ1(t)=S4(t,ΔT1,s1)
θ2(t)=S4(t,ΔT3,s2)

(27)

(2)目标函数。为同步优化SCARA机器人的定位效率和受到的冲击,选取末端定位时间和加速度的时间导数为优化目标。设定位精度为ε,则定位时间可用公式表达为:

(28)

末端加速度的时间导数可表达为:

(29)

(3)约束条件。两个驱动自由度的速度、加速度、急动度及急动度导数均不能超过给定的最大值,对应为vm、am、jm、dm,因此,约束条件可以表达为:

(30)

综上所述,SCARA机器人运动规划问题的数学模型可表达为:

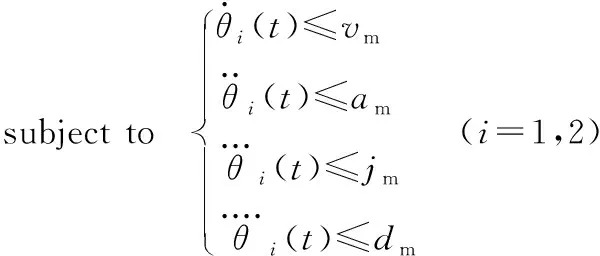
(31)

求解式(31)时需要进行大量的动力学仿真分析,计算效率较为低下。因此,本文采用基于Kriging代理模型的NSGA-Ⅱ算法对式(31)进行求解,通过构造目标函数与约束函数的Kriging模型代替原函数,提升优化过程的计算效率。

3 仿真验证

SCARA机器人的结构参数如表1所示,目标位置与运动学约束等优化参数如表2所示,目标位置为rt=[0.3 0.4]T,对应的关节位移为Q1=0.453 8 rad,Q2=1.317 1 rad,机械臂末端的定位精度取为ε=1×10-9m。

表1 SCARA机器人结构参数

表2 SCARA机器人末端目标位置及运动学约束参数

调用MATLAB软件的“gamultiobj”函数对运动规划问题式(31)进行求解,算法的参数设置如表3所示。为便于对比,采用工程中广泛应用的三阶S形曲线构造与式(31)类似的多目标优化问题并进行求解。三阶S形曲线和四阶S形曲线得到的Pareto前沿分别如图3和图4所示,对应的优化目标和约束函数值分别如表4和表5所示,表中obj-1为定位时间,obj-2为末端加速度的时间导数,con-1、con-2、con-3分别为关节1的速度、加速度、急动度约束,con-4、con-5、con-6分别为关节2的速度、加速度、急动度约束。

表3 多目标优化算法参数设置

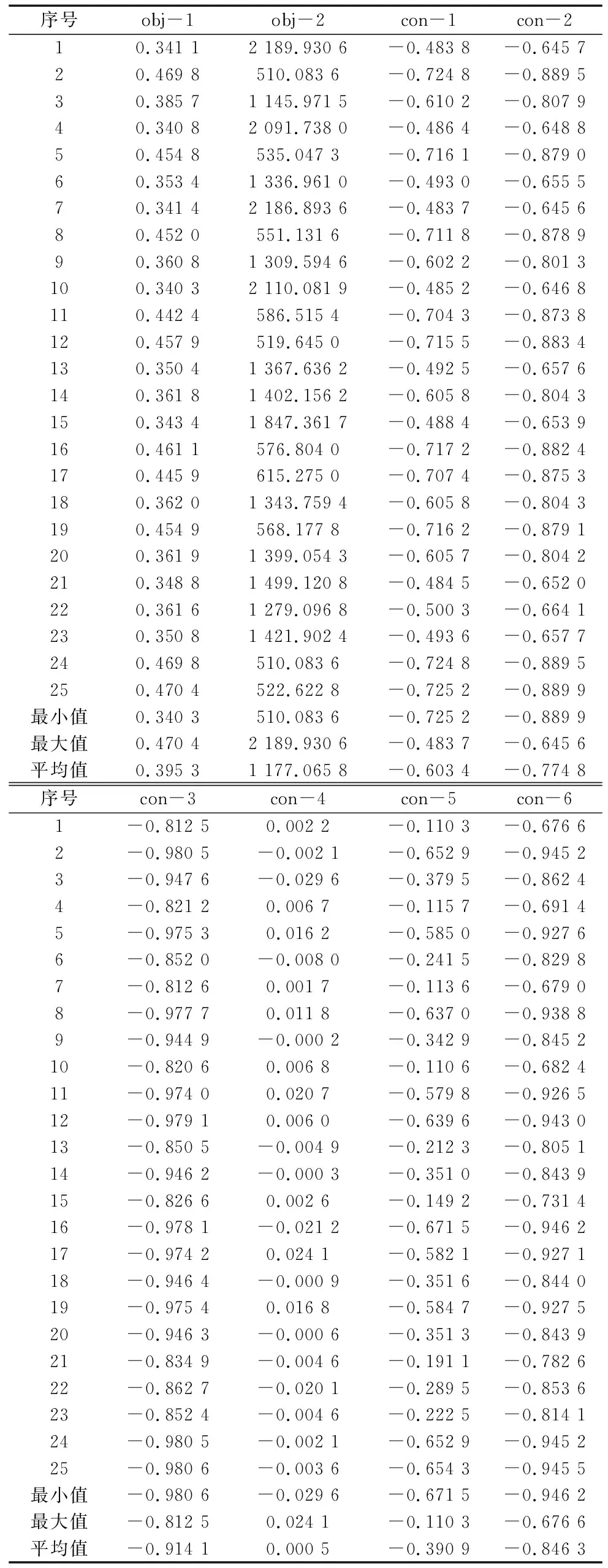
表4 三阶S形曲线优化目标与约束函数值

表5 四阶S形曲线优化目标与约束函数值

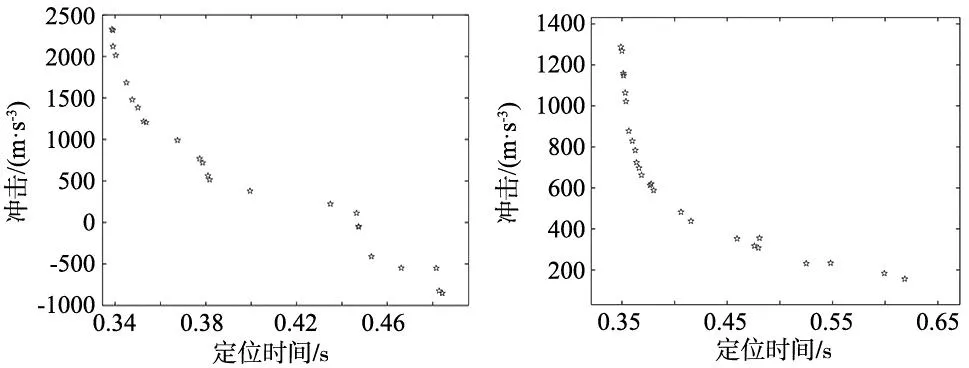
图3 三阶S形曲线Pareto前沿 图4 四阶S形曲线Pareto前沿

由表4和表5数据可以看出,三阶S形曲线和四阶S形曲线得到的Pareto前沿都满足约束条件。从定位时间来看,三阶S形曲线的最优解为0.340 3 s,略少于四阶S形曲线的最优解0.349 0 s,定位时间的最大值和平均值方面也是三阶S形曲线的结果略优。从机器人受到的冲击来看,三阶S形曲线的最优解为510.083 6 m/s3,远大于四阶S形曲线的最优解156.066 1 m/s3。从冲击的最大值和平均值来看,也是本四阶S形曲线胜出。

分别取三阶S形曲线和四阶S曲线的最短定位时间解进行仿真分析,得到的关节变形量、末端定位过程和受到的冲击分别如图5～图7所示。由图5可知由于关节柔性的存在会导致一定的变形量,三阶曲线和四阶曲线得到的变形量大致相当,其中关节1的最大变形量约为关节2的2倍。由图6可知,三阶S形曲线和四阶S形曲线都能使SCAARA机器人准确定位到目标位置,其中四阶S形曲线引起的残余振动远小于三阶S形曲线。由图7可知,三阶S形曲线引起了数值较大的高频冲击,而四阶S形曲线引起的冲击数值较小,频率也较低。

图5 关节变形量曲线 图6 末端定位过程曲线

图7 末端冲击曲线

4 结论

本文建立了用于振动分析的SCARA机器人简化浮动坐标法动力学模型,并利用n阶S形曲线和基于Kriging模型的多目标优化方法对其进行振动抑制运动规划。数值仿真结果表明,相比于三阶S形曲线,四阶S形曲线能够更有效地减少SCARA机器人运行过程中的冲击,从而实现更加平滑的运动过程,达到振动抑制的目的。定位时间方面,四阶S形曲线比三阶S形曲线没有明显的增加,由此可见四阶S形曲线在定位效率和振动抑制方面具有性能上的优越性,在工程中具备广泛的应用价值。