简化计算的改进PMSM模型预测电流控制算法
邓 斌,张 博,艾雄雄,王 杰,张立昌
(1.西安工程大学 电子信息学院,西安 710600; 2.西安工程大学 工程训练中心,西安 710600)
0 引 言
永磁同步电机(以下简称PMSM)具有效率高、结构简单、功率密度大等优势,是电动汽车、精密机床、航空航天等高性能运动控制领域的关键器件之一[1-2]。在直接转矩控制、矢量控制、滑模变控制等众多控制策略中,模型预测控制因其滚动优化、易处理多目标非线性约束的优势,成为了PMSM高性能控制领域拥有广大应用前景的控制策略[3]。
模型预测电流控制(以下简称MPCC)是模型预测控制的重要研究分支。传统MPCC只能输出固定的8个电压矢量,难以对系统稳态时的微小误差进行调节,因此存在较大的电流波动,相电流畸变严重,同时计算量大也是阻碍MPCC实现规模应用的主要因素之一[4]。为此,文献[5]提出了一种占空比MPCC策略,能任意调节输出矢量的幅值,降低了传统MPCC的稳态电流波动,但输出电压矢量的方向固定。文献[6]提出了双矢量MPCC策略,与占空比MPCC相比,该策略第二个矢量的选择范围不再局限于零矢量,因而能调节输出矢量的幅值和方向,进一步减小了电流波动。但需进行14次寻优计算,计算量大,且逆变器开关频率较大,不便于实际应用。文献[7]通过分析给定电流与预测电流的误差,仅需一次计算就能确定最佳电压矢量,大幅减小了计算量,但对电流波动的改善有限。文献[8]在文献[7]的基础上,提出了一种改进型减少计算负担(以下简称RCB)的控制策略即RCBII-MPCC,该算法在每个扇区确定3个备选电压矢量组合并通过轴电流无差拍原理计算矢量作用时间,把价值函数取值最小的电压矢量组合输出到电机,在减轻计算负担的同时有效降低了电流波动,并遵循一相开关跳变原则,减少了逆变器的开关频率,降低了开关损耗。
本文在RCBII-MPCC算法的基础上,将整个电压矢量平面重新划分为12个扇区,使备选电压矢量组合由3个减少为2个,提高了算法运行效率。为了降低电流波动和相电流畸变,基于电流无差拍控制原理构建了电压矢量作用时间与d,q轴电流误差的函数,分析得到了MPCC价值函数最小值的取值规律,提出了一种简化最优电压矢量作用时间的计算方法,最后通过改进方式快速确定最优矢量组合并作用到电机。与传统MPCC算法相比,该算法在减少计算量的同时有效改善了电机的输出特性。
1 传统PMSM的MPCC方法
1.1 PMSM数学模型
采用id=0的控制策略,以表贴式永磁同步电机(以下简称SPMSM)为研究对象。在旋转坐标系下,忽略电机定子铁心饱和,不计电机的涡流及磁滞损耗,SPMSM的数学模型列写如下:
定子电压方程:
(1)
式中:ud,uq为d,q轴电机定子电压分量;id,iq为d,q轴电机定子电流分量;Ls为定子电感;Rs为定子电阻;ψf为永磁体磁链;ωe为转子电角速度。
电磁转矩方程:
(2)
式中:p为电机极对数。
1.2 传统MPCC的基本原理
基于式(1)的SPMSM数学模型,可以得到离散化后的预测电流:
(3)
式中:id(k+1),iq(k+1)为d,q轴定子电流在下一时刻的预测值;ud(k),uq(k)为当前时刻d,q轴定子电压;id(k),iq(k)为当前时刻d,q轴定子电流;Ts为采样周期。
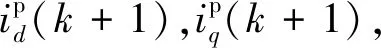

(4)
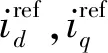
2 改进PMSM的MPCC算法
2.1 参考电压矢量位置角的计算
传统MPCC通过遍历寻优的方式选取最优电压矢量,计算量大。本文通过电流无差拍原理求取参考电压矢量的位置角[10],以确定其所在的扇区,据此直接得到两个备选电压矢量组合,避免了遍历寻优带来的计算负担。
(5)
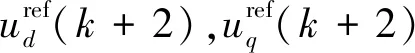
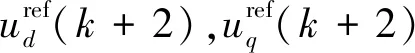
(6)
2.2 扇区划分与备选矢量组合选取
RCBII-MPCC算法将电压矢量平面划分为6个扇区,每一个控制周期都需进行3次寻优计算。本文通过细化扇区的方式,将电压矢量平面划分为12个扇区,由此将候选电压矢量组合减少为2组,有效降低了计算量,提高了算法的运行效率[11]。扇区划分方式如图1所示:
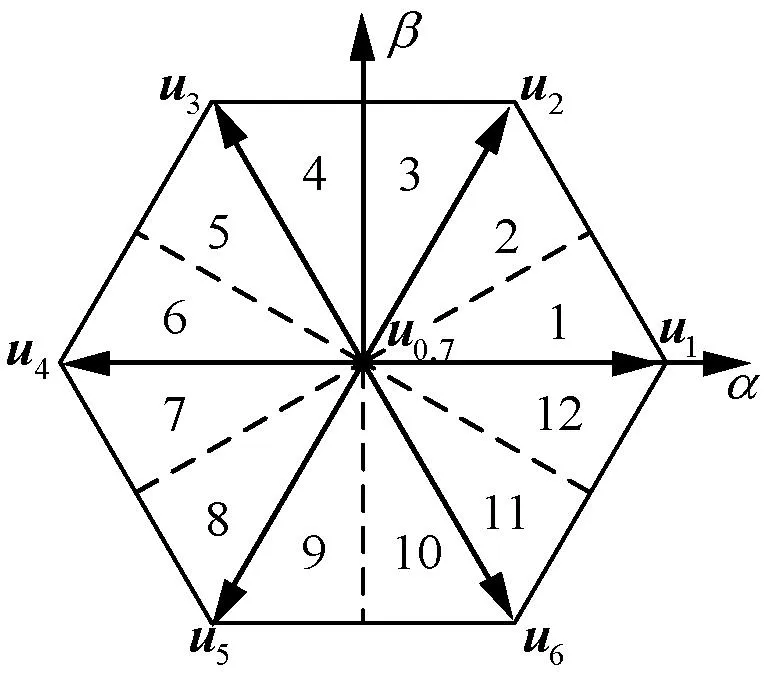
图1 改进算法的电压矢量平面扇区分布
在两相静止坐标系下,记α轴正方向为0点,逆时针每旋转30°划为一个扇区,每个扇区产生两组备选电压矢量组合。备选电压矢量组合与扇区位置关系如表1所示。
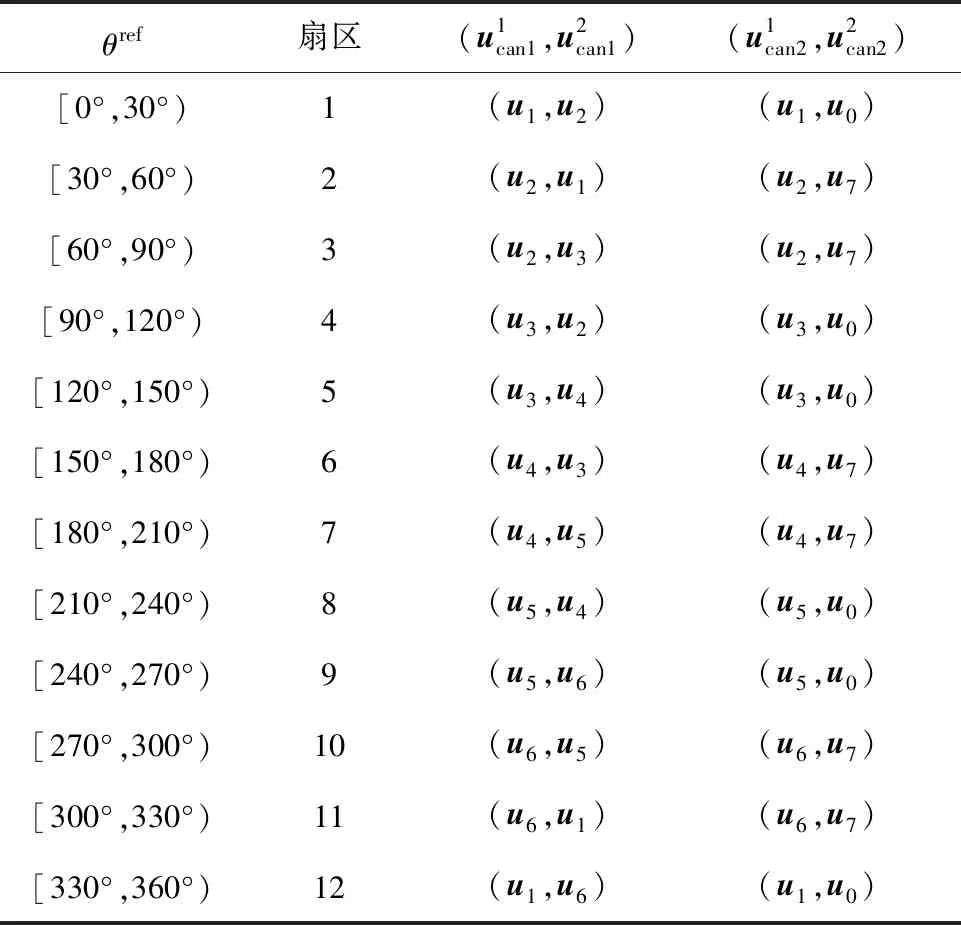
表1 备选电压矢量组合与扇区之间的关系
2.3 矢量最优作用时间的计算
传统双矢量MPCC通常采用q轴电流无差拍原理计算电压矢量作用时间,而该作用时间并非MPCC价值函数的最优解,从而导致d轴电流波动较大,三相电流总谐波畸变率较高,无功功率损耗严重。本文提出了一种简化最优矢量作用时间的计算方式,使MPCC价值函数达到最小,并尽量减少因求取电压矢量最优作用时间所带来的计算量。
基本电压矢量作用下,电机d,q轴定子电流变化率[12]:
(7)
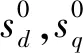
(8)
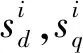
考虑一拍延时补偿,在备选电压矢量组合(u1,u2)的作用下,下一时刻的电流:
(9)

(10)
当备选电压矢量组合确定后,式(10)中唯一的变量即t1。为便于分析,构建误差函数e(r):
e(r)=(s1-s2)r+s2-C
(11)
式中:r为自变量,取值范围为任意实数;s1,s2,C为常值。
将等式(10)等号左边部分分别表示为Cd,Cq,并以式(11)表示:
(12)
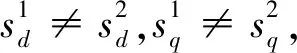
g=|ed|+|eq|
(13)
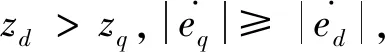
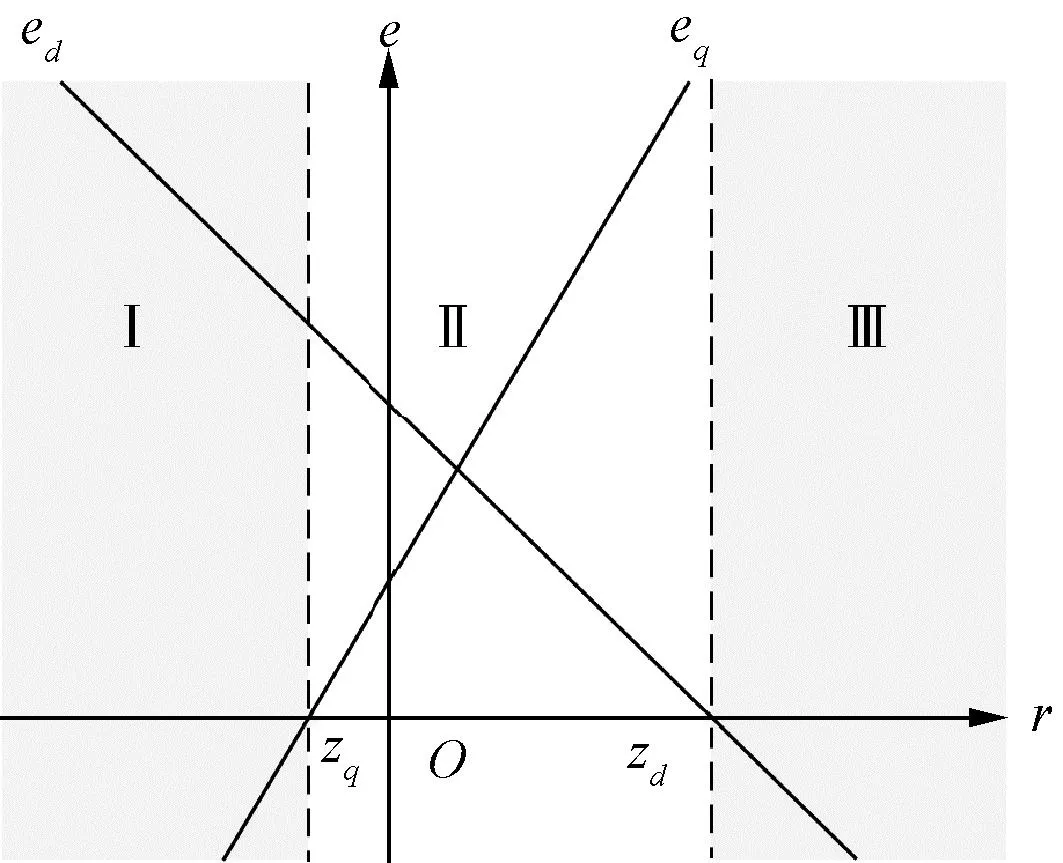
图2 rOe平面上ed,eq图象
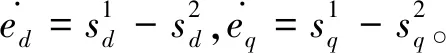
本文提出的控制方式如下:
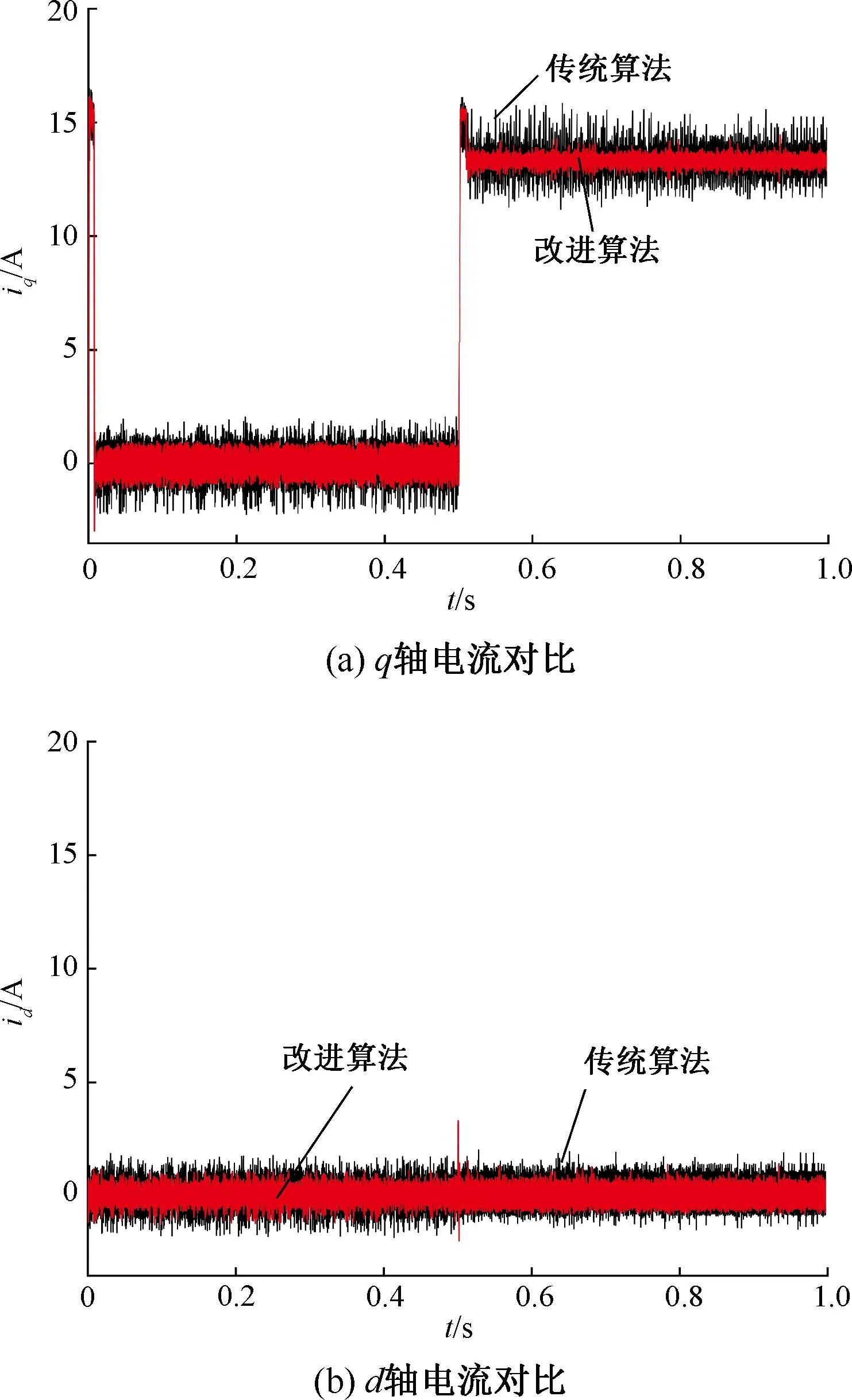
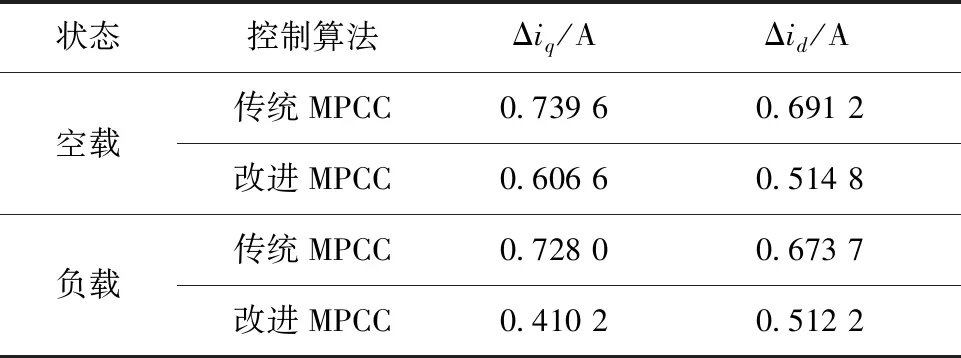
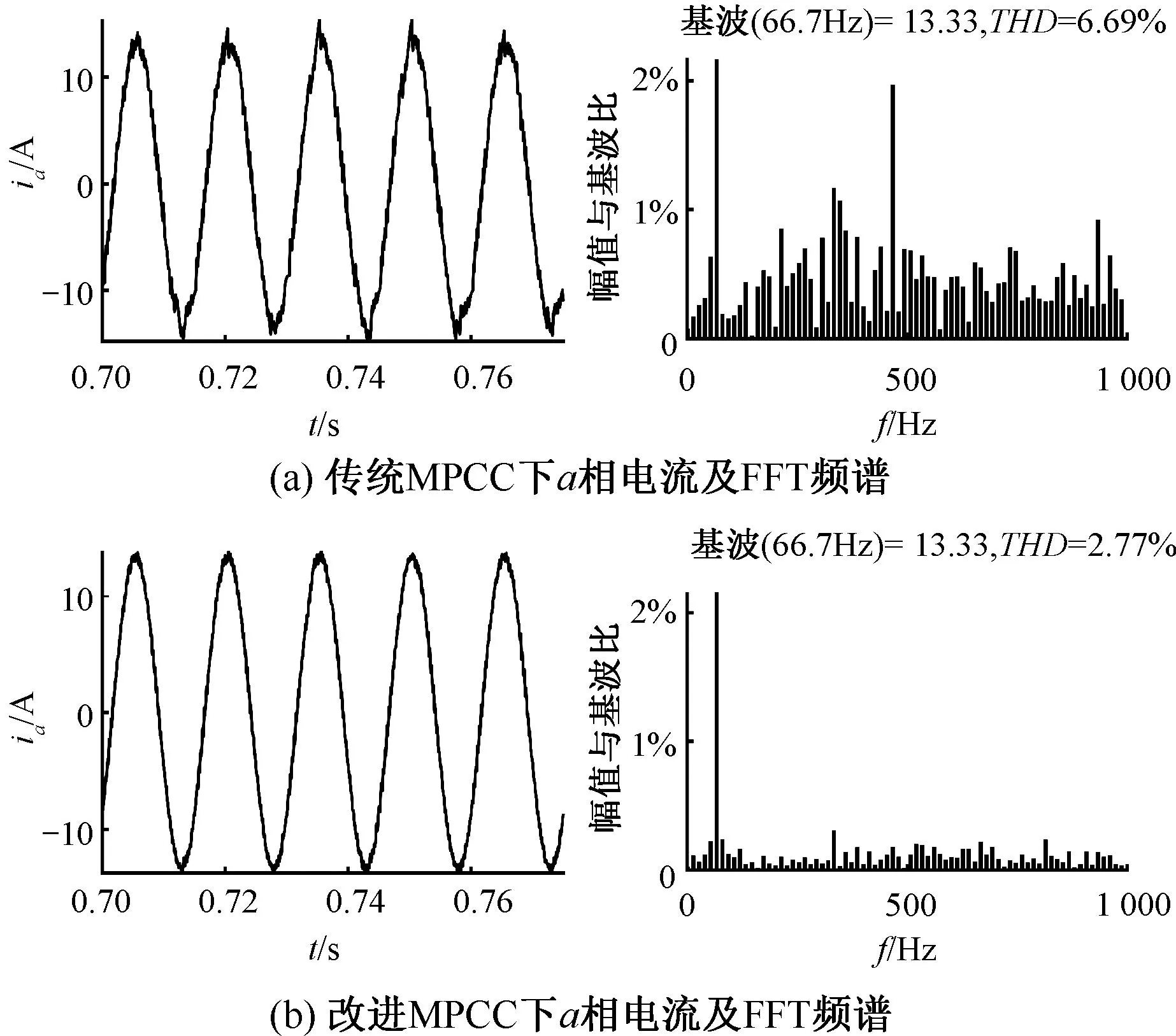
1)当0 2)当mg≥1时,备选电压矢量组合中第一个矢量u1的作用时间t1=Ts,该控制周期只作用u1。 3)当mg≤0时,备选电压矢量组合中第一个矢量u1的作用时间t1=0,该控制周期只作用u2。 为了验证本文的改进MPCC算法的有效性,基于MATLAB中的Simulink模块进行了仿真实验。将传统MPCC算法与本文算法进行对比分析。仿真中的电机参数如表2所示。仿真中速度环PI参数均保持一致,控制周期设为50 μs。 表2 PMSM参数表 仿真总时长为1 s。仿真过程:电机空载起动,转速由零升至额定值,保持稳定运行,在0.5 s时突加12 N·m的负载转矩,然后保持稳定运行至仿真结束。图3是两种控制算法作用下电机的d、q轴电流对比图。 图3 不同MPCC算法下的d,q轴电流 定义稳态下空载(0.05 s~0.50 s)和负载(0.55 s~1.00 s)电流波动计算公式: (14) 式中:N为采样点总数;iq(n),id(n)分别为仿真中q,d轴的采样值;iq_ave,id_ave分别为q,d轴电流平均值。根据式(14),计算电机在空载和负载时不同MPCC算法下的电流波动值,如表3所示。 表3 不同MPCC算法下的电流波动 分析图3和表3,传统MPCC算法由于在一个控制周期内只能输出一个电压矢量,因此在系统稳态时存在过调节和欠调节的问题,电流波动很大。而本文的改进MPCC算法能够根据最小化MPCC价值函数原则在一个控制周期内输出一个或两个电压矢量,因此能够明显减小电机的d,q轴电流波动。尤其在负载状态下,电机的q轴电流波动大幅减小。 图4是加上负载并达到稳态后(0.70 s~0.75 s),两种算法下的a相电流波形及对应的FFT分析频谱对比图。传统MPCC控制算法下的电机定子电流畸变严重,相电流THD达6.69%,谐波较大。而改进MPCC得益于其对d,q轴电流波动的改善,最终相电流THD降低为2.77%。 图4 两种控制算法下的相电流波形及谐波分析 图5是0.70 s至0.75 s时间段内,在改进MPCC算法下系统最终输出的电压矢量,其中输出的第一个电压矢量uact1,在6个有效电压矢量中选择,总体上其取值从u1至u6循环往复,在扇区交界处来回切换,图形呈阶梯状,表明参考电压矢量在电压平面上作逆时针旋转。输出的第二个电压矢量uact2,选择范围包含全部的8个电压矢量,需要指出的是,当uact1的作用时间为整个周期时,uact2实际并未输出。由于遵循一相开关跳变原则,uact2在uact1的相邻有效电压矢量或零矢量中选择,因此其图形与uact1基本一致,而零矢量的选择参考uact1,使其在u0和u7间依次轮换。因此,改进MPCC的稳态性能较好。 图5 改进MPCC的输出电压矢量 本文提出了一种改进MPCC算法。该算法基于无差拍原理计算参考电压矢量位置角,直接得到两个备选电压矢量组合,避免了遍历寻优计算,然后通过一种改进方法求取电压矢量最优作用时间,并简化了最优矢量组合的选取步骤。通过仿真实验表明,相较于传统的MPCC算法,该算法可以有效减少电流波动,降低相电流的波形畸变,且稳态性能较好。在尽量减少计算量的同时,仍保持了良好的控制效果。2.4 最优矢量组合的选取
3 结果分析


4 结 语