基于灰狼算法的无轴承永磁同步电机多目标优化
周晓燕,张庭恺,朱来澳,卢庆轩,吴昊昱
(青岛理工大学 信息与控制工程学院,青岛 266525)
0 引 言
永磁同步电机具有效率高、功率密度高、容错性能强、结构相对简单等优点,广泛应用于各行各业[1]。无轴承永磁同步电机是电机领域的一项突出的创新和应用。无轴承永磁同步电机具有非接触承载能力,从根本上改变了传统的支承型式,从而避免了机械摩擦带来的能量损耗和故障。在能源交通、航空航天、机械工业及机器人等高科技领域得到了广泛的应用[2-4]。
在寻找最优电机设计方案的过程中,电机结构和尺寸的变化会对电机的性能造成影响。为了找到最优的电机设计方案,许多智能优化算法被应用到电机优化设计中。在优化设计中使用较多的方法主要有:模拟退火算法、差分进化算法、粒子群算法及遗传算法等[5]。文献[6]使用多目标粒子群算法对开槽参数进行优化来改善开关磁阻电机的转矩性能,优化后其性能得到显著提高。文献[7]通过构建响应面,并采用遗传算法对永磁无刷电机的反电动势值、总谐波畸变率和齿槽转矩进行了优化。虽然通过响应面法优化后电机的性能得到显著提升,但是响应面法的局限性是不能保证响应面通过所有的样本点,并且响应面法所设计的实验点应当包括最佳的实验条件,如果实验点选取不当,优化结果会不理想。文献[8]建立同步磁阻电机的有限元模型,采用田口优化方法,分析磁通屏障的数量、位置和尺寸对静态转矩特性的影响,优化结果显示选择合适的转子几何形状能够有效地改善静态转矩特性和转矩脉动。而田口法的计算精度较差,考虑的不全面并且对数据的预处理增加了实验设计的复杂性。文献[9]基于磁场解析模型和带精英策略的非支配排序遗传算法对内置式永磁同步电机的0阶12倍频径向力波、转矩和效率进行优化,优化后电机的各项性能得到的显著提升,实现了多目标多参数的快速优化,验证了解析模型和优化算法相结合的优化方法的有效性。文献[10]通过建立开关磁阻电机的有限元模型,对转子齿形进行参数化,研究其对转矩脉动的影响并进行优化。但是有限元法分析时,其优化效率并不高,且优化过程既复杂又耗时。
解析法能够清晰地反映出电机优化参数和目标函数之间的关系,而且计算时间短,降低了优化设计的复杂性。本文针对表贴式无轴承电机,结合解析法和多目标灰狼算法,对电机进行优化设计,以电机的悬浮力脉动和转矩作为优化目标,将得到的最终优化结果和有限元法进行对比,验证了多目标优化的正确性。
1 电机的基本结构及解析模型的的建立
1.1 电机有限元模型
图1为4极15槽的表贴式无轴承电机的有限元模型。槽内为双层绕组,上方为悬浮绕组,下方为转矩绕组。电机的基本结构参数如表1所示。
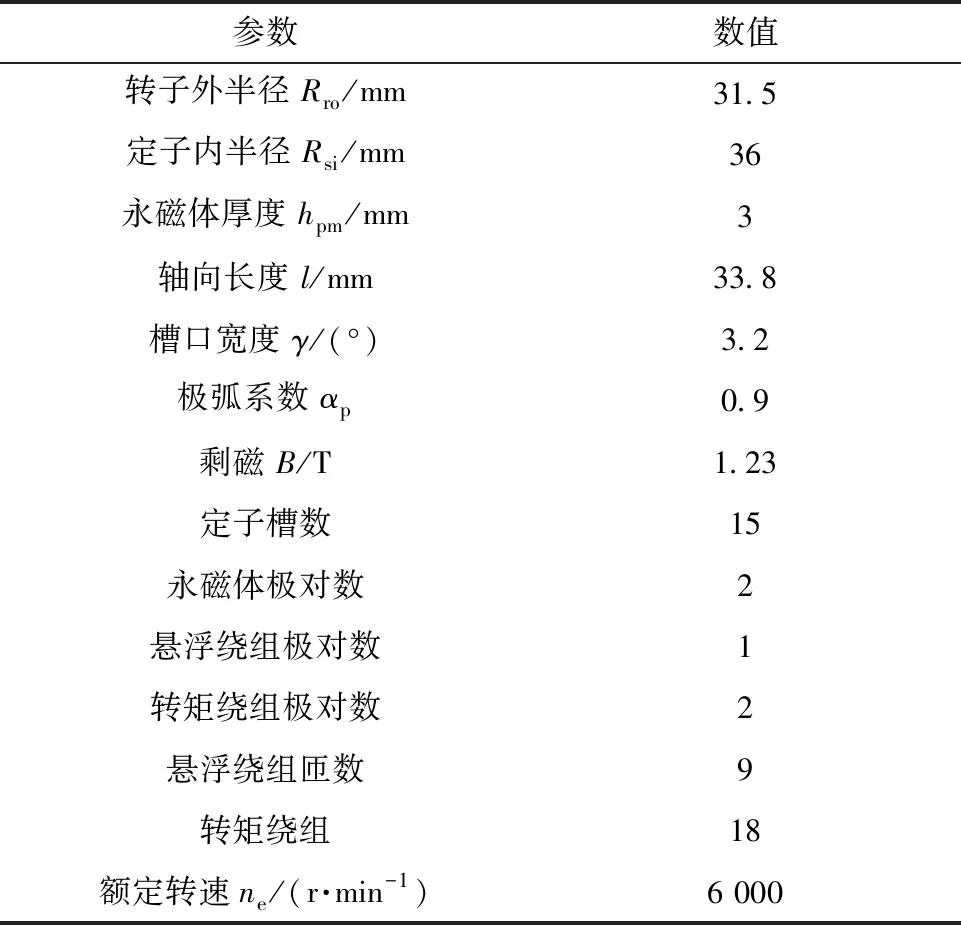
表1 样机参数
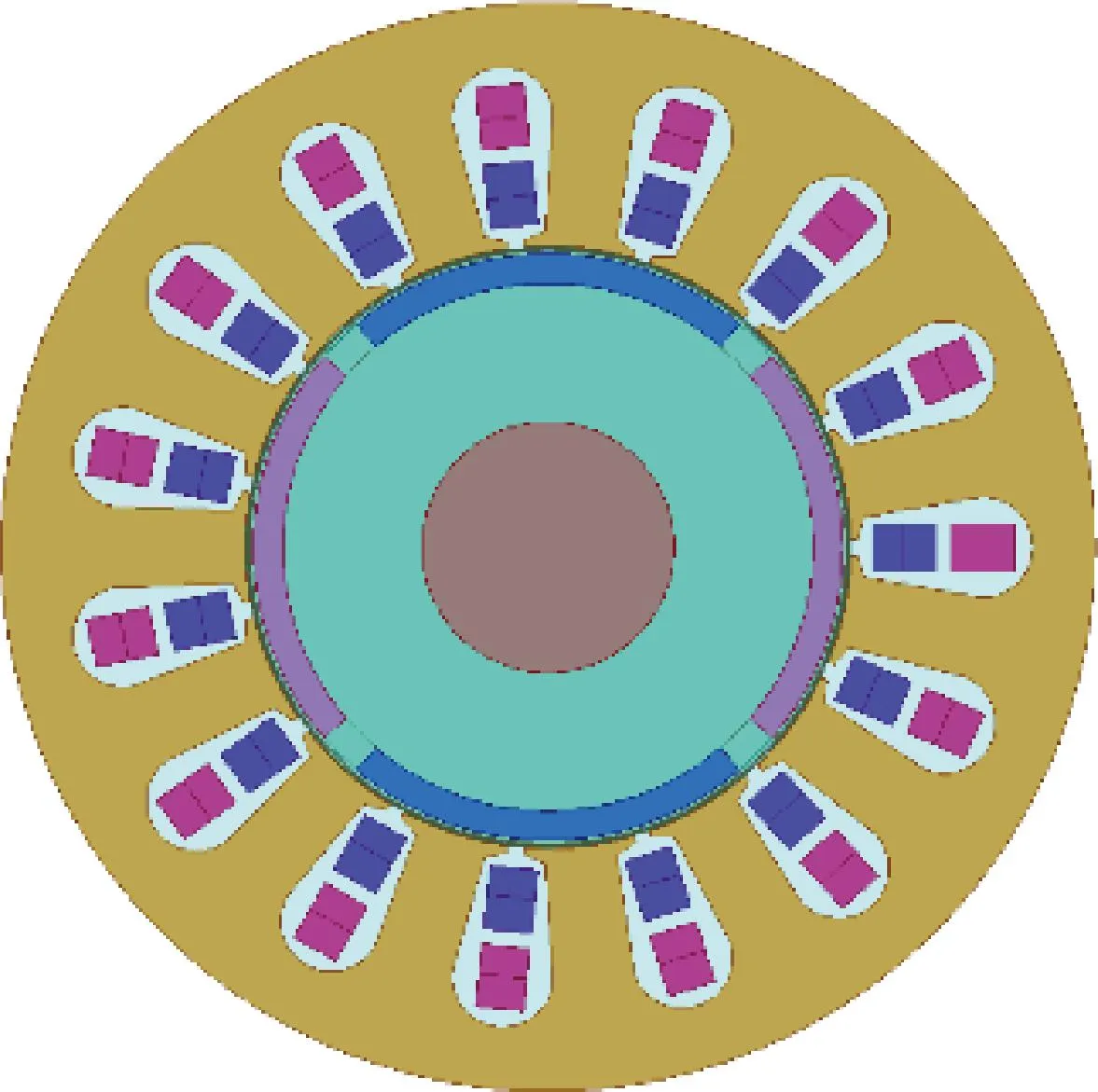
图1 电机有限元模型
1.2 解析模型的建立
本文对表贴式无轴承电机的结构进行分析,将电机划分为3个求解区域:气隙区域、永磁体区域和定子槽区域。为了便于分析,简化数学模型,作如下假设:定、转子铁心的磁导率无穷大;永磁体径向充磁且相对磁导率为1;不考虑电机的磁饱和效应;定子槽型简化为扇形结构。
电机的二维平面图如图2所示。

图2 简化后电机剖面图
各个子区域的矢量磁位方程满足:
(1)
式中:μ0为真空磁导率;M为永磁体的磁化强度;下标i代表第i个定子槽;J为电流密度。
各个子域之间的边界条件:
(2)
将边界条件代入到式(1)中,根据分离变量法,永磁体区域的通解:

(3)
气隙区域的通解:
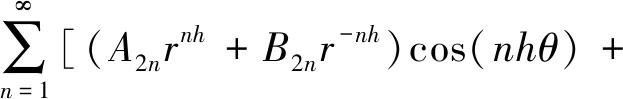
(4)
由于定子槽内的绕组为上下双层排布,定子槽区域的通解:
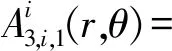
(5)
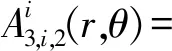
(6)
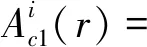
(7)
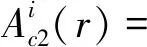
(8)
式中:k为定子槽谐波数。
将所求得的矢量磁位的通解代入式中,可以得到径向和切向气隙磁密Br和Bθ:
(9)
2 瞬态磁场解析计算及验证分析
根据电机的解析模型,编写MATLAB程序来计算电机的径向、切向气隙磁密和悬浮力。利用ANSYS Maxwell建立表贴式无轴承电机的有限元模型,对电机的径向、切向气隙磁密和悬浮力进行计算,并和解析法计算的结果进行对比来验证解析法的准确性。
图3为解析法和有限元法以r=(Rs+Rm)/2为半径的空载气隙磁密波形。可以看出,二者的结果非常相似,但是在幅值上两种方法存在着微小的偏差,这是因为解析法没有考虑磁饱和等因素的影响。
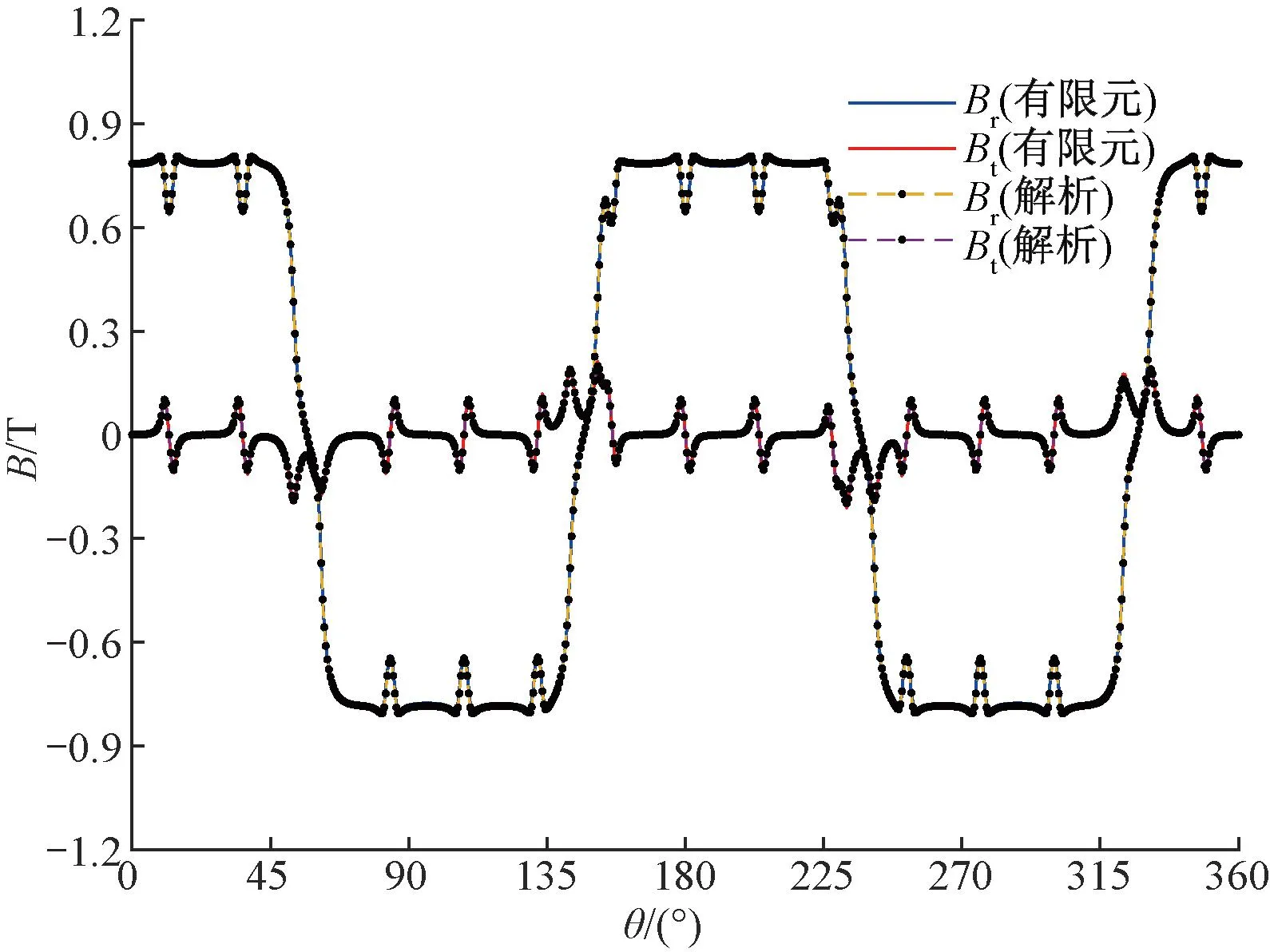
图3 气隙磁密对比
利用麦克斯韦张量法可以得到沿x轴和y轴方向上的磁拉力,具体表达式如下:
(10)
应用麦克斯韦张量法计算转矩,可以表示:
(11)
调整悬浮电流的相位,使其获得y轴正方向的悬浮力。图4和图5为悬浮绕组和转矩绕组加载i=3 A的电流时解析法和有限元法计算的悬浮力和转矩的对比。可以看出,在负载情况下,解析法计算的峰值比有限元法的结果要大一些,但有限元法和解析法计算结果基本一致。误差产生的原因可能是解析法简化了定子槽的槽型和有限元法的网格剖分,有限元法和解析法计算的悬浮力和转矩的对比进一步证明了解析法的正确性。
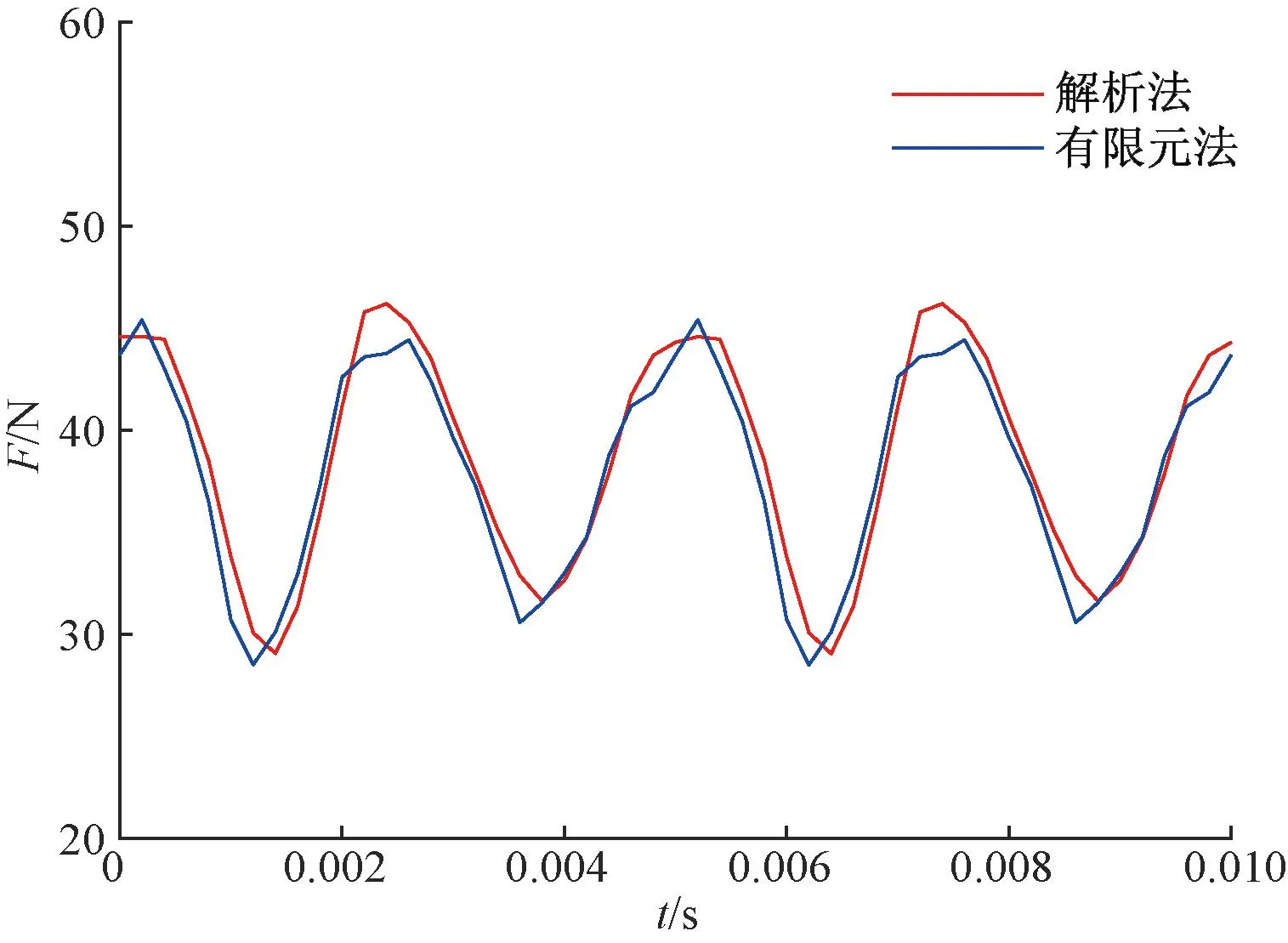
图4 负载电流3 A时悬浮力对比(解析法和有限元法)
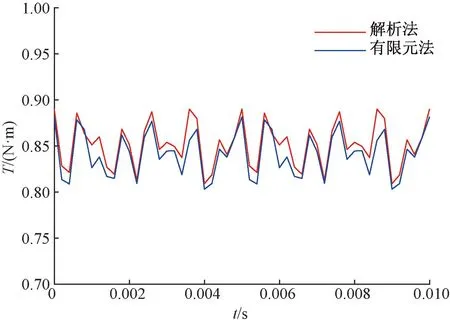
图5 负载电流3 A时转矩对比(解析法和有限元法)
3 多目标灰狼算法
3.1 确定优化目标和优化参数
为了使无轴承电机的性能更优越,将电机的悬浮力脉动ΔF和平均转矩Tavg作为优化目标,使电机的悬浮力脉动更小的同时能够提升电机的平均转矩。定义悬浮力脉动ΔF:
(12)
根据所设置的优化目标,多目标优化的目标函数可以表示:
(13)
当进行电机的设计参数优化时,各个参数的自由度很大,并且还要考虑到其之间的制约性,因此选取哪几个变量对于电机的优化设计非常关键。根据经验选择气隙宽度、永磁体厚度、极弧系数和槽口宽度这4个对悬浮力影响比较大的参数进行优化,表2给出了所选优化参数的合理变化范围。

表2 电机模型优化设计变量
3.2 多目标灰狼优化
多目标灰狼算法是由Mirjallii等人[11]在灰狼算法的基础上进行改进,在保持灰狼算法优秀性能的前提下,引入外部种群Archive来存储非支配解并集成网格机制来提高非支配解的质量。
灰狼算法是通过观察自然界中狼群的社会等级制度和包围狩猎的行为而提出的。其中包围猎物的数学公式如下:
D=|C×Xp(t)-X(t)|
(14)
X(t+1)=Xp(t)-A×D
(15)
A=2a×r1-a
(16)
C=2r2
(17)
式中:Xp为猎物的位置向量;X为灰狼的位置向量;D为灰狼与猎物之间的距离;A和C为系数向量,t为当前迭代次数;r1和r2是0到1之间的随机向量;a表示收敛因子,其变化规律是线性减小的,可以用a=2×(1-t/T)计算,其中T为总的迭代次数。
灰狼的种群可以分为4个阶层,分解为α,β,δ和ω。其中最优解为α狼,第二和第三好的解为β和δ狼,其余的候选解为ω狼。在算法迭代的过程中,由α,β和δ来引导,ω狼跟随这三只狼来寻找最优解。其中猎杀猎物的数学公式如下:
(18)
(19)
(20)
式中:Dα,Dβ,Dδ分别为灰狼个体与3个领导狼α,β,δ之间的距离;X1,X2,X3分别为在α,β,δ引导下的位置向量;X为ω狼的位置。
3.3 优化结果分析
验证电机解析程序的正确性之后,将解析程序和多目标灰狼优化结合,对目标函数进行优化,使电机的性能达到想要的结果。图6为两个目标函数优化的Pareto前沿。
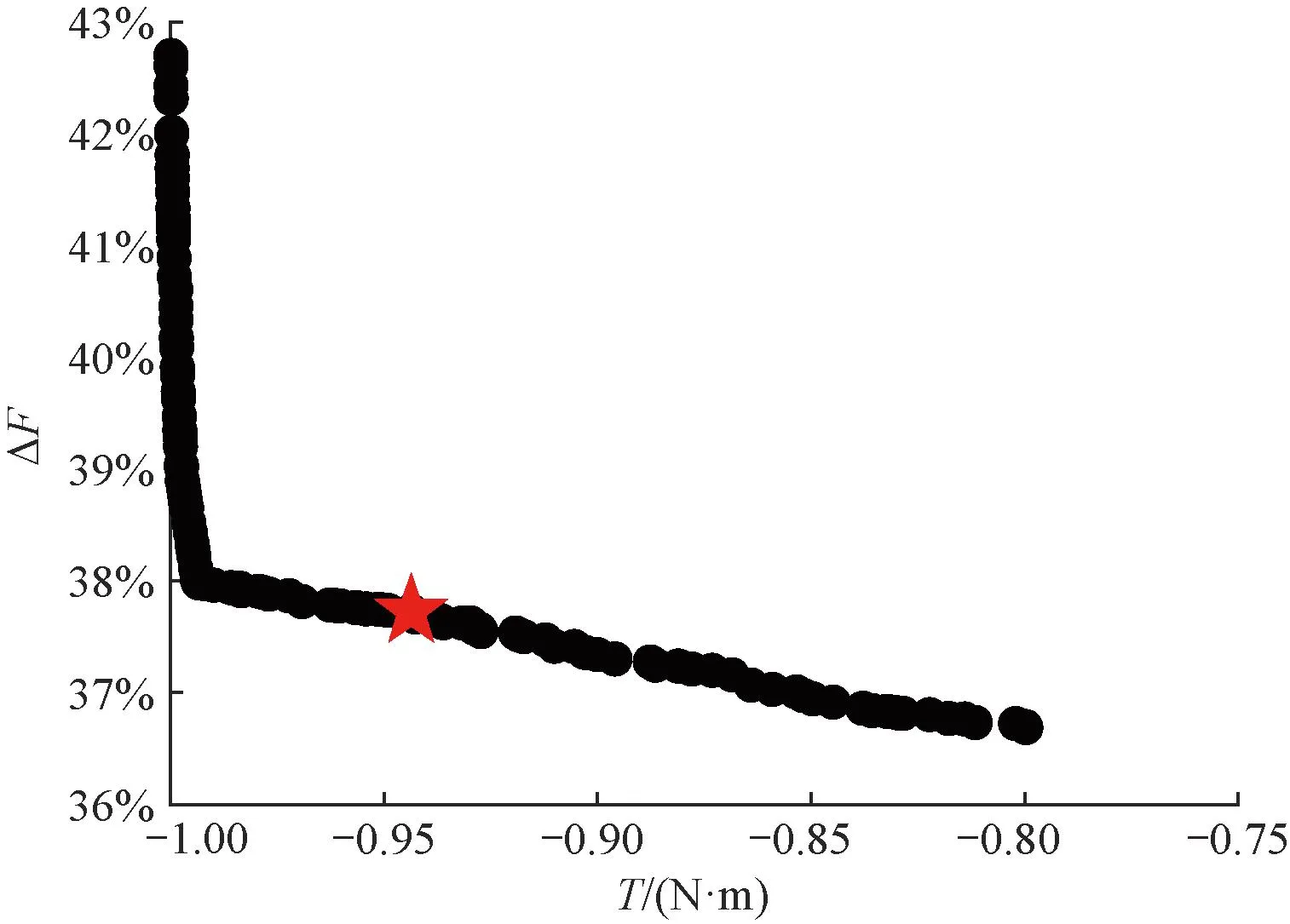
图6 目标函数Pareto前沿
在Pareto前沿形成的解集都是可行解,但是在选择中不仅要考虑更大的转矩和更小的悬浮力脉动,悬浮力的大小也要满足电机能够正常运转的条件,综合考虑后,选择星型为最终的优选方案。优化前后的各项参数如表3所示。
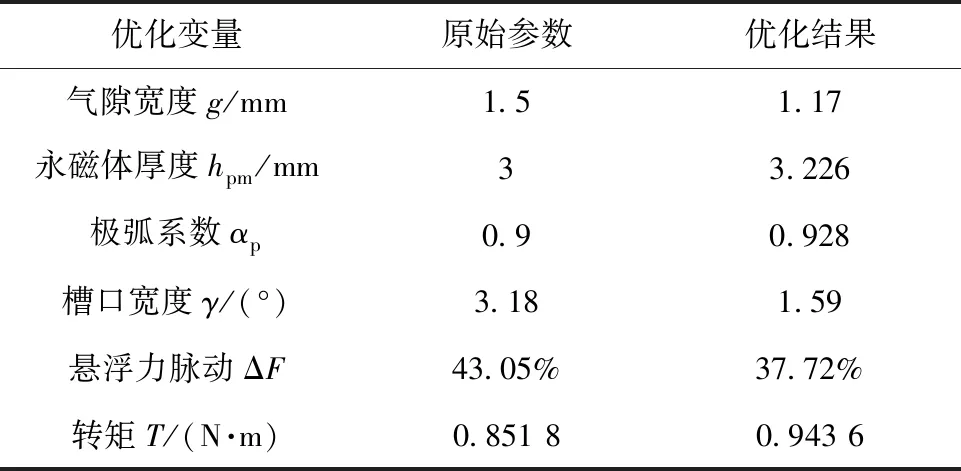
表3 优化前后参数对比
由表3可以看出,优化后,悬浮力脉动减小了5.33%,较优化前减小约12.38%;平均转矩增大了0.091 8 N·m,较优化前增大约10.78%。
为了进一步验证优化结果的有效性,将优化后的各项参数导入有限元模型中进行计算,在不同负载的情况下对优化前后的电机性能进行对比。
通过图7和图8可以看出,优化后电机的平均悬浮力随着电流的不断增加,其幅值整体要比优化前的更大。优化后的悬浮力脉动随着电流的不断增大,其幅值要比优化前的更小。电机获得了更好的悬浮性能,证明了优化方法的有效性。

图7 不同负载电流时,优化前后悬浮力对比
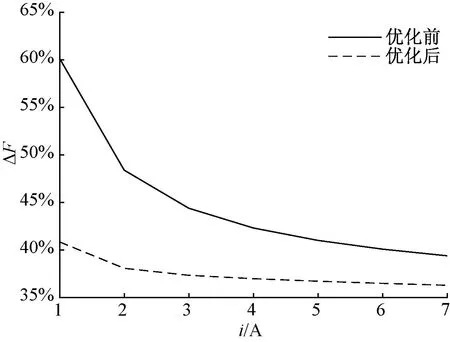
图8 不同负载电流时,优化前后悬浮力脉动对比
图9为优化前后平均转矩随着电流不断增大的对比结果。可以看出,优化后的平均转矩比优化前的整体幅值更大,电机获得了更大的转矩,达到了优化目标,证明了优化方法的有效性。

图9 不同负载电流时,优化前后转矩对比
电机的悬浮绕组和转矩绕组各加载i=3 A的电流,对比优化前后的结果如图10和图11所示。
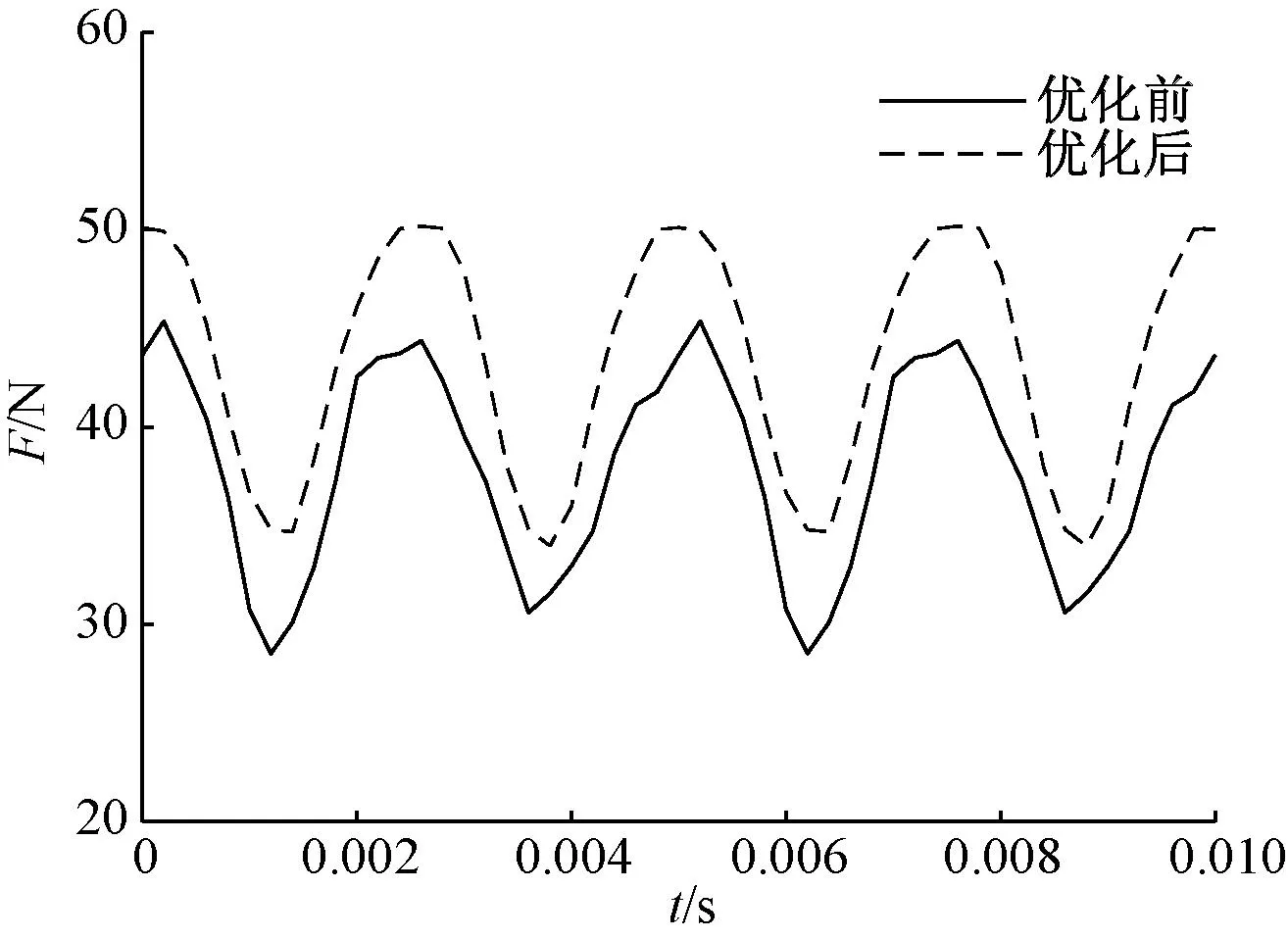
图10 负载电流3 A时,优化前后悬浮力对比

图11 负载电流3 A时,优化前后转矩对比
悬浮力脉动由原来的44.297%减小到37.220%,比原来下降了15.98%,平均转矩由原来的0.841 N·m增加到0.929 N·m,比原来增加了10.46%,同时悬浮力大小也满足电机能够正常运行的条件。验证了优化的有效性,显著提升了无轴承永磁同步电机的性能。
4 结 语
本文针对表贴式无轴承电机的特点,结合子域法构建电机的解析模型。通过计算不同负载情况下的气隙磁密、平均悬浮力和转矩波形,与有限元法进行比较,验证了解析法对表贴式无轴承电机求解的准确性。
结合解析法和多目标灰狼算法对表贴式无轴承电机进行优化设计,以悬浮力脉动和转矩作为目标函数,气隙宽度、永磁体厚度、极弧系数和槽口宽度作为优化变量。优化后电机的悬浮力脉动减小了12.38%,转矩提升了10.78%,电机性能得到了明显的改善。
将得到的优化方案导入Maxwell中进行计算并和优化前的电机性能进行对比,优化后的电机性能得到了不同程度的提高,并且和解析法计算结果基本吻合,证明了优化算法的有效性。