异步电机永磁悬浮轴承结构设计与动力学计算
葛研军,龙 威,于 涵,马雪祺,董法强
(大连交通大学 机械工程学院,大连 116028)
0 引 言
悬浮支撑或微摩擦支撑对改善设备振动、噪声,提高系统高速性能的可靠性并增加轴承使用寿命等均具有重要意义[1]。磁悬浮轴承是通过磁力实现悬浮支撑的新型轴承,包括主动式磁悬浮轴承与永磁轴承。
主动式磁悬浮轴承通过电磁铁产生磁力,是典型的机电一体化产品,通过负反馈控制对磁场强弱进行调整实现无接触支撑,其缺点是造价昂贵、需要复杂的控制系统与外加电源[2]。
永磁轴承无需主动电子控制系统,仅利用永磁体磁场即可实现转子稳定悬浮,避免了繁复的电子元器件故障所引起的系统失效[3],目前已在宇宙飞船[4]、飞轮储能[5]、人工心脏[6]、风力发电[7]等领域得到应用。永磁轴承主要缺点是无法实现五自由度悬浮[8],支撑刚度较低[9]。通过将磁环反向叠加布置,可使轴向充磁的永磁轴承刚度得到有效提升[3]。
本文将调心滚子轴承与永磁轴承相结合,提出一种转子微摩擦结构,即利用永磁轴承实现转子径向稳定悬浮,利用调心滚子轴承限制永磁轴承在高势能状态下的轴向位移,并使之不产生轴向力,保证转子在径向及轴向方向始终处于微摩擦状态。
为确定永磁轴承的径向刚度为最小值,本文首先基于气隙磁导法确定出不平衡磁拉力的刚度;然后对反向叠加式永磁轴承结构进行优化,获得有限体积内永磁轴承的最大支撑刚度;最后,通过对转子刚度的计算结果、转子临界转速及其刚体定点旋转轨迹的分析计算,验证了所提支撑结构的可靠性。
1 电机结构设计
图1为本文提出的微摩擦支撑异步电机结构。
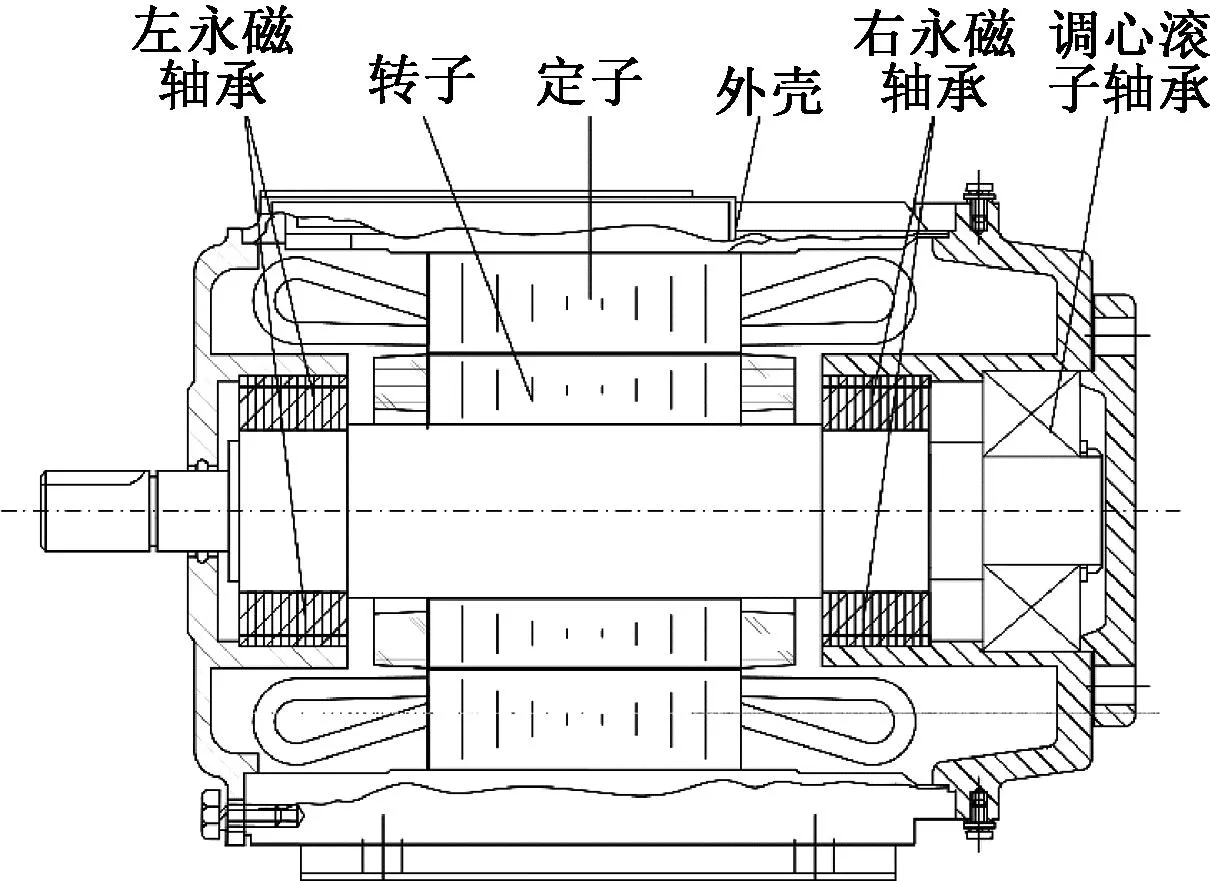
图1 电机结构图
图1中的永磁轴承对称放置在转子两端,并在转子尾部采用一个调心滚子轴承承受转子所受的轴向力,这样可使永磁轴承的内、外磁环保持在同一轴向平面内,使机械轴承始终处于一种微摩擦状态。当转子受径向力时,调心滚子轴承可在2°~3°范围内偏转,在此状态下,转子的径向力主要由永磁轴承承担,图1的机械轴承受力仍较小,因而可保证转子的微摩擦支撑。
2 永磁轴承设计
2.1 电机不平衡磁拉力分析
电机转子做定点转动时,转子偏转会使磁场在整个圆周范围内产生畸变,引起不平衡磁拉力[10]。不平衡磁拉力(UMP)是转子偏心故障的主要原因[11],因此需要永磁轴承具有足够的支撑刚度以克服UMP引起的电机转子偏转。本文以Y2-712-2型电机为研究对象,电机参数值如表1所示。
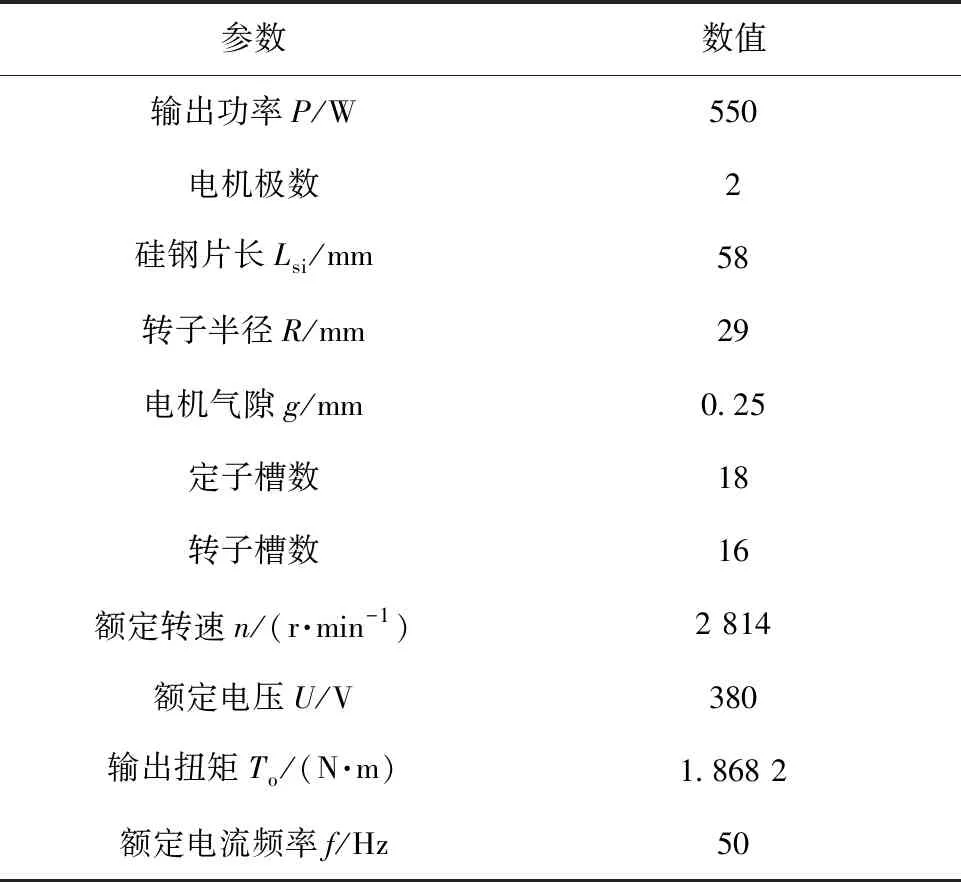
表1 电机主要参数
图2为有限元法计算表1电机参数在无永磁轴承作用时的UMP与其偏心率之间的关系曲线。
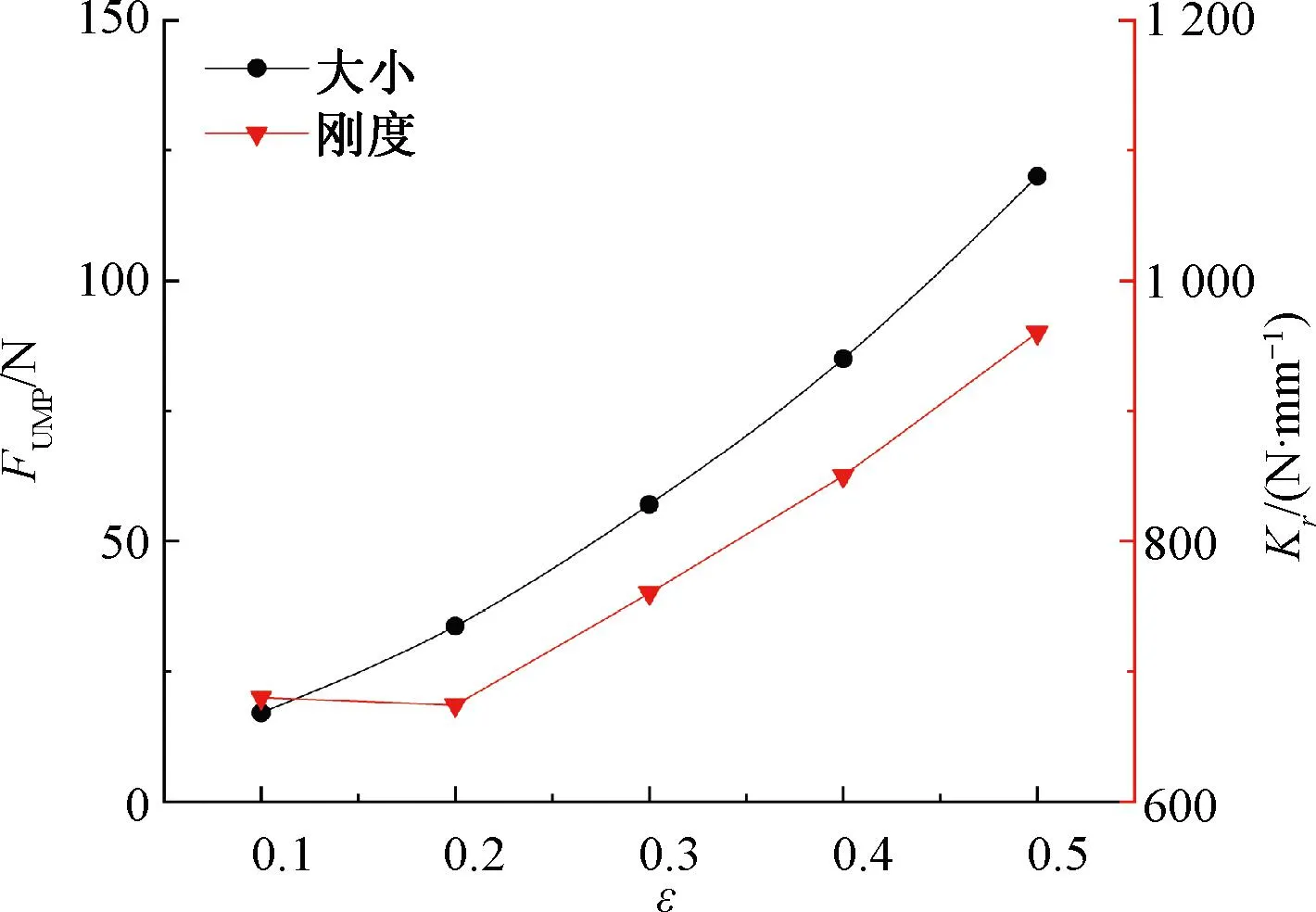
图2 UMP与偏心率关系曲线
由图2可知,随着偏心率的增大,不平衡磁拉力与刚度均增大。
2.2 等效磁荷法计算磁力
图3为轴向磁化的永磁轴承模型。
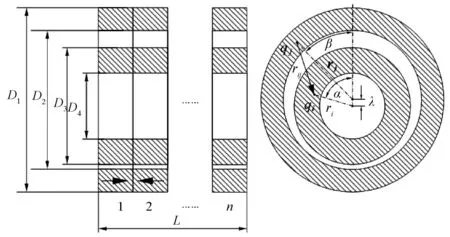
图3 轴向磁化的永磁轴承模型
图3中,D1及D2分别为定子外径及内径,D3及D4分别为转子外径及内径,总轴向长度为L,分割环数为n,λ为径向偏移距离,qi、qj分别为内磁环与外磁环上的磁荷点,rij为外磁环磁荷点到内磁环磁荷点的矢量,ri、rj分别为内磁环与外磁环上的磁荷点到圆心的距离,α、β分别为内磁环与外磁环上的磁荷点所在的角度,g为气隙长度。
由磁库仑定律知,磁荷点间的磁力:
(1)
式中:μ0为空气磁导率。
由磁化关系可得:
(2)
式中:Bri、Brj为磁环的剩磁大小。本文使用牌号为N35的钕铁硼,其剩磁为1.23 T。
将式(1)在磁荷面上积分,则图3模型的磁荷面间作用力可表示:
(3)
对所有内、外磁环磁荷面间作用力求矢量和,即可得到永磁轴承内、外磁环作用力。
2.3 有限元与算法对比
设图3中D1=50 mm,D2=40.2 mm,D3=39.8 mm,D4=30 mm,多磁环轴承的总轴向长度L=20 mm,n=10,可得如图4所示的不同轴向偏移下的轴向力对比。

图4 三维有限元法与等效磁荷法图
由图4可知,三维有限元法结果与等效磁荷法结果具有密切一致性(最大误差仅为8%),验证了等效磁荷法的可靠性。
2.4 结构参数确定
本文轴承的初始参数:D1=50 mm,D2=40.2 mm,D3=39.8 mm,D4=30 mm,L=20 mm,n=10。在总体积不变的条件下,调节气隙长度g、气隙所在位置、磁环分割数目n,以获取最大的径向刚度Kr。
1)气隙长度g
图5为不同气隙与径向偏移时永磁轴承的径向刚度曲面。由图5可知,径向刚度随气隙的减小而增加,相同气隙长度下,不同径向偏移时永磁轴承的径向刚度几乎不变。但过小的气隙会造成永磁轴承装配困难,综合考虑,本文取g=0.2 mm。
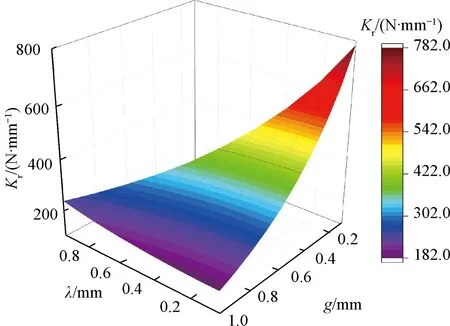
图5 刚度、偏移、气隙之间的关系
2)转子外径D3与分割环数n
图6为g=0.2 mm时,径向刚度Kr与D3、n等高线图。

图6 Kr与D3、n等高线图
由图6可知,当分割环数在1~40变化,转子外径在44.0~49.2 mm之间变化时,永磁轴承刚度的极大值出现在D3=46.8 mm,n=27处,为1 262 N/mm。
取径向刚度最大时的轴承参数,可得如表2所示的永磁轴承的结构参数表。
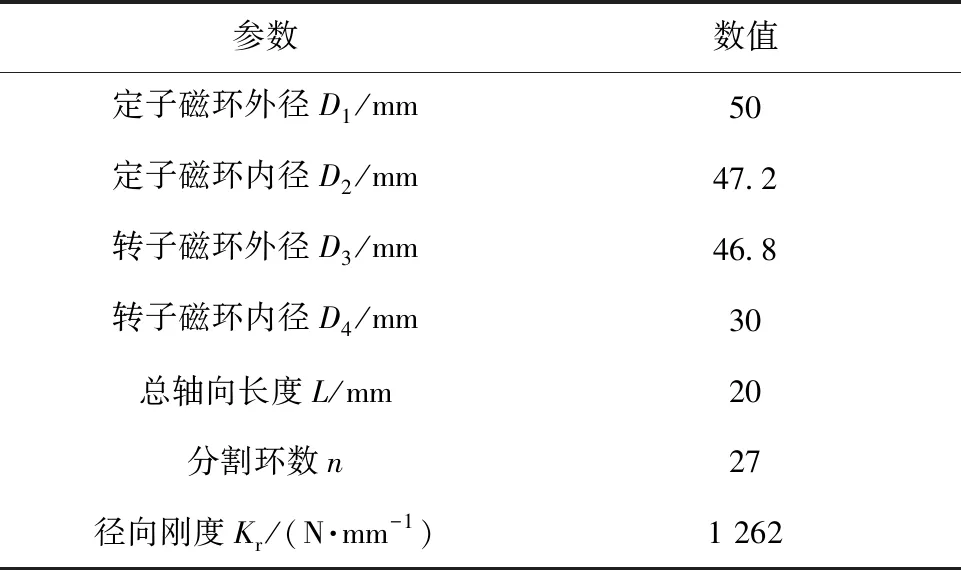
表2 径向刚度最大时永磁轴承主要参数
3 转子涡动分析
刚体定点转动将产生偏转,为避免内、外磁环之间的径向接触,需要对转子定点转动的静止与起动过程进行分析。
3.1 动力学模型
由于调心滚子轴承的支撑刚度远大于永磁轴承与UMP刚度,且可在一定角度内偏转[13],故可将转子运动模型简化成以中心轴为对称轴线的对称陀螺模型,如图7所示。
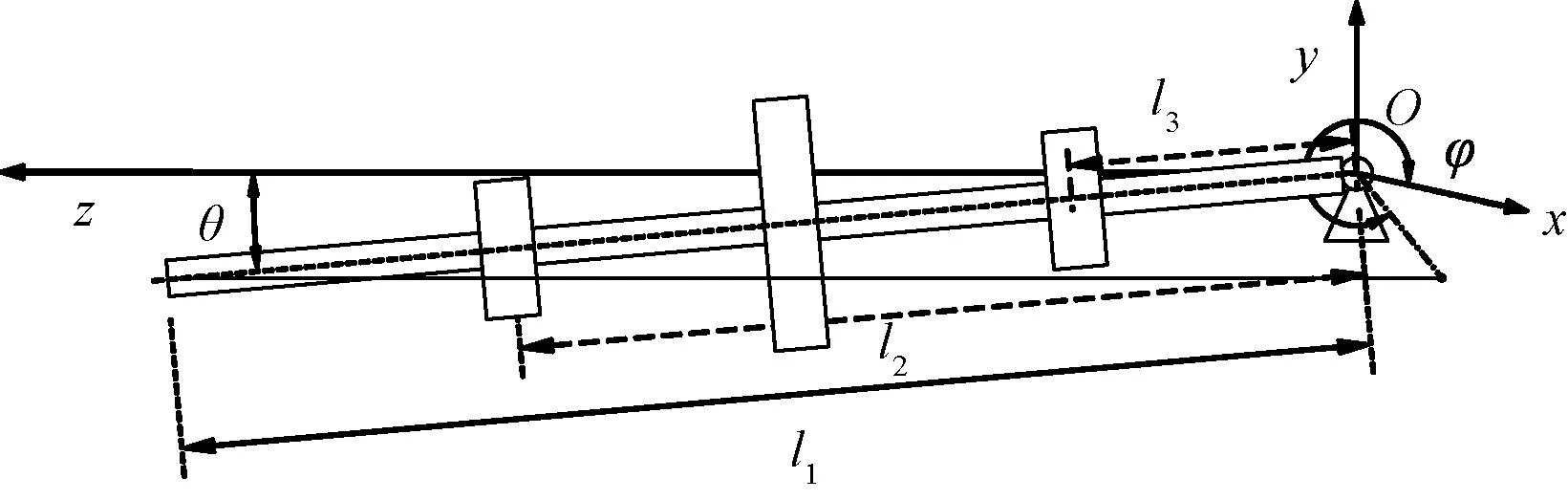
图7 转子运动模型
图7中,O点为固定点,l1为转子输出端到旋转中心的距离,l2及l3分别为左永磁轴承与右永磁轴承到调心滚子轴承的距离,θ为转子相对于z轴的偏转角度,φ为转子轴线在xOy面上的投影与x轴的夹角,m为转子质量。
为方便分析转子静止与起动过程中的输出端运动轨迹,对图7参数赋值,l1=170 mm,l2=140 mm,l3=30 mm,结合转子径向尺寸可得转子对z轴的转动惯量I3为7.84×10-4kg·m2。
3.2 静止状态
电机静止时,图7的转子不平衡磁拉力为零,此时转子的重力与磁轴承径向力平衡,其所形成的偏转角θ=0.000 07 rad。由于左永磁轴承的最大径向偏移为0.010 5 mm,远小于永磁轴承气隙0.2 mm,转子的最大径向偏移为0.007 7 mm,远小于电机气隙0.15 mm,故图7模型可满足静止状态的支撑要求。
3.3 起动与运行过程
由图7的转子几何关系可知:
(4)
(5)
式(4)及式(5)中:I1、I2及I3分别为转子对于x、y、z轴的转动惯量,ω0为转子的自转角速度,Ωx、Ωy、Ωz分别为转子在x、y、z轴上的进动角速度。
偏转角度θ较小,可忽略其对转子所受电磁转矩的影响。由图7可知,转子所受力矩:
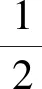
(6)
式中:ME为异步电机电磁转矩,其大小与转速相关,可由Kloss公式求得。
由初始条件可得:
(7)
将式(7)代入式(6)即可获得起动与运行过程中的M与θ及φ的关系。
图8为转子起动过程中输出端轴心轨迹。

图8 转子输出端轴心轨迹
由图8可知,转子输出端以(0,-0.010 5 mm)为圆心、0.001 65 mm为半径做转子涡动,其最大偏移为0.012 mm,远低于电机气隙与永磁轴承气隙。
4 临界转速分析
电机工作在临界转速附近时,转子将会产生共振,从而导致转子传动失效。Riccati矩阵传递法是常用的临界转速计算方法,其主要步骤为轴段划分、参数集总化、求解传递矩阵。
4.1 转子轴段划分
转子轴段划分是矩阵传递法计算的第一步,通常选在截面突变处以及轴的支撑位置,其划分数目应满足:
N≥1+5.34r
(8)
式中:N为划分轴段数,r为要求解的临界转速阶数。本文求解前4阶转速,划分段数为39。
图9为转子轴段划分与支撑点位置图。图9中Ⅰ、Ⅱ、Ⅲ、Ⅳ分别为左永磁轴承支撑处、不平衡磁拉力作用处、右永磁轴承支撑处与调心滚子轴承支撑处。
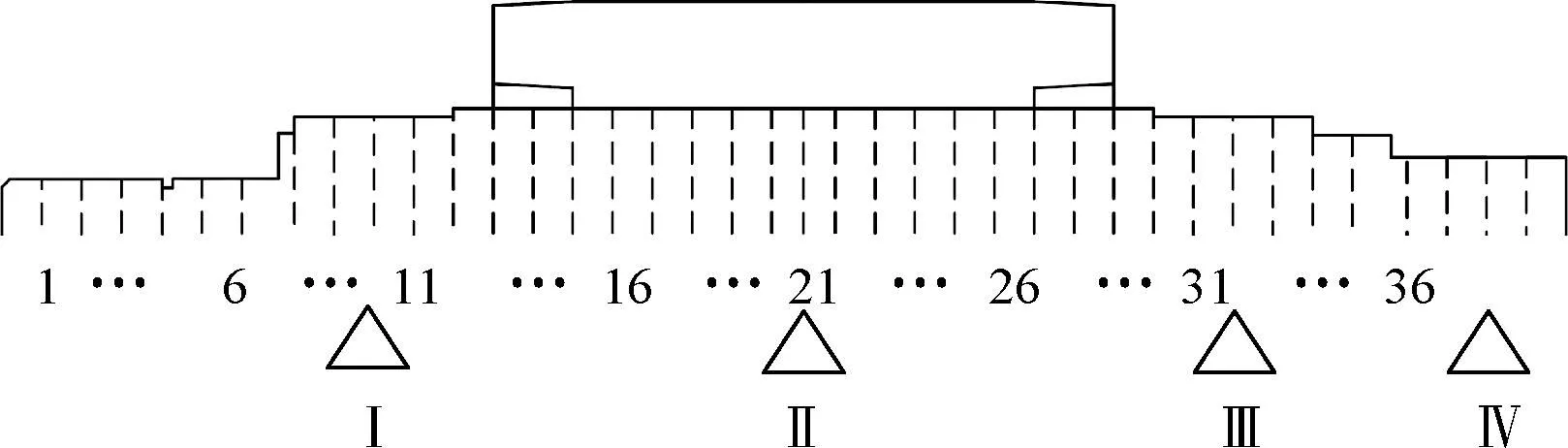
图9 转子轴段划分与支撑位置
表3为部分转子离散轴段集总化参数。

表3 部分转子集总化参数
4.2 支撑点及其刚度
偏心率大于10%时,认定电机发生偏心故障[14],故本文取偏心率为10%时的刚度值计算。由图9可知,转子共计三个支撑点,支撑点与不平衡磁拉力作用参数如表4所示。
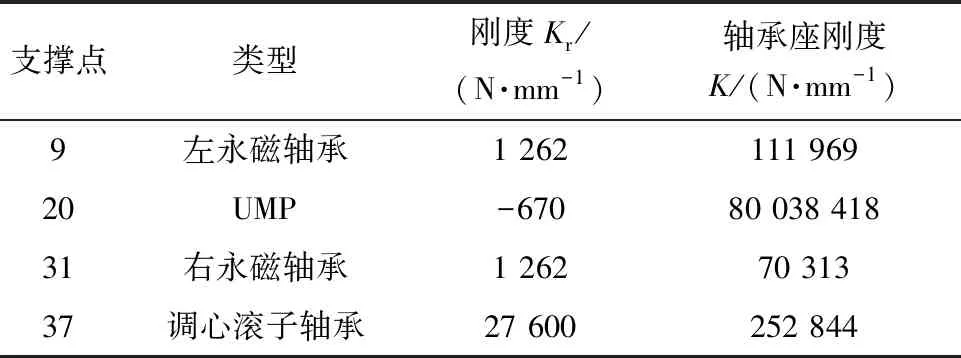
表4 支撑点及不平衡磁拉力刚度大小
4.3 求解传递矩阵
图10为基于Riccati矩阵传递法求解表3、表4参数所获得的剩余量-转速曲线。图10中剩余量缓慢下降为零的转速取值即为临界转速。
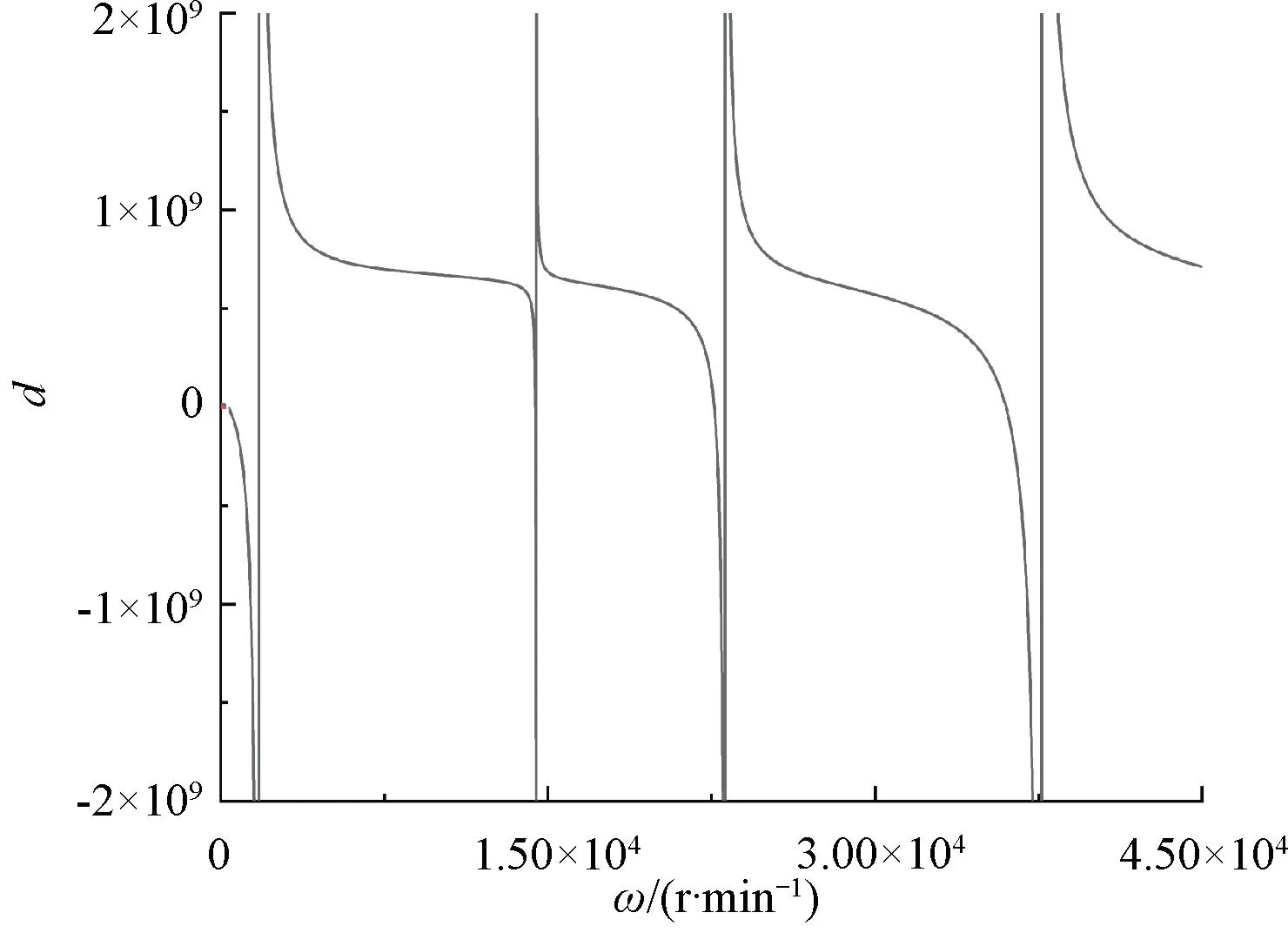
图10 剩余量-转速关系
表5为转子各阶临界转速。

表5 转子各阶临界转速
由于转子的安全转速范围是1.4ωcn~0.7ωcn+1,故本模型可在0~1 305 r/min、2 610~10 091 r/min转速内运行。
5 结 语
本文采用一个调心滚子机械轴承限制电机的轴向位移,构成刚体定点转动模型。基于涡动轨迹分析与临界转速分析两个要素对转子模型进行分析,验证了微摩擦五自由度支撑结构的可靠性。
永磁轴承的转子径向刚度对气隙长度敏感,而对径向偏移距离不敏感,且在体积一定条件下存在一个最佳的分割环数与气隙位置,可使永磁轴承径向刚度获得最大值。
通过Riccati矩阵传递法计算出本文转子的前四阶临界转速分别为1 864.5 r/min、14 417 r/min、22 624 r/min、33 143 r/min,其安全转速范围包括0~1 305 r/min、2 610~10 091 r/min。