湿煤聚团与弛张筛筛板碰撞解聚的离散元模拟

唐 弦，熊晓燕，唐 建

（太原理工大学机械与运载工程学院，山西 太原 030024）

1 引言

由于待筛的原煤含有一定水分，细粒物料由于水作用容易粘结成聚团，形成堵塞筛孔的现象，进而造成筛分效率下降［1-2］。文献［3］通过采用独特的聚氨酯筛板及其弛张运动，使筛面具有较大的振动强度，因而能够有效地处理潮湿细粒物料黏附成团和堵塞筛孔等问题。文献［4］通过理论计算认为，影响筛分效率的主要原因是颗粒在液桥力的作用下发生了黏附成团。文献［5-6］从理论的角度研究了颗粒碰撞分离的机理，得出颗粒在液桥力作用下发生分离的条件和临界初速度；并基于二维离散元法模拟总结了聚团与刚体碰撞解聚的三种分离模式，并对其中的重力-碰撞式分离式进行了力学分析，使用高速摄像机拍摄了聚团与金属板的碰撞行为并揭示了包衣结构团聚体的碰撞解聚过程和机理。文献［7］利用EDEM与粘结模型分析了等径团聚体与刚性体筛板的碰撞解聚机理及其影响因素。

通过筛分实验确定湿煤聚团粒径组成，并采用液桥力接触模型模拟颗粒间及颗粒与筛板间液桥力的作用，基于EDEM液桥力接触模型API和实验数据构建模拟实际情况的中心非球形大颗粒与非等径小颗粒相结合的湿煤聚团模型，建立EDEMRecurDyn联合模拟分析了湿煤聚团与柔性体弛张筛板的碰撞解聚过程与机理，对比分析了湿煤聚团与静止筛板和弛张筛板碰撞解聚，并研究了不同偏心距对聚团碰撞解聚的影响。

2 颗粒间液桥力接触

2.1 液桥力理论

根据水含量的不同，含水物料间的液桥存在摆动状、环索状、毛细管状、浸渍状四种状态。对于待筛分的原煤，其外在质量含水量一般处于（7～14）%之间，此时颗粒间的液桥互不相连，呈现摆动状态［8］。假设聚团颗粒间液体分布是均匀的，此时对于两球形颗粒间和颗粒与平面间液体形成的液桥，可以用一段圆弧来近似替代表示液桥与大气的气液相交界面轮廓；两球形颗粒间液桥、球形颗粒与平面间液桥示意图，如图1所示。R、Ri、Rj—球形颗粒半径；θ—固液接触角；V—液桥体积；h—两球形颗粒表面间距和颗粒表面与平面间的间距。

图1 液桥力原理Fig.1 Principle of Liquid Bridging Force

文献［9］通过回归分析方法得到颗粒间液桥力与液桥体积以及颗粒表面间距的显函数关系：

式中：Ri、Rj—形成液桥的两球形颗粒i，j的物理半径；A、B、C—液桥体积V、颗粒半径的函数。对于两球形颗粒间有：

对球形颗粒和平面有：

式中：V∗—无量纲液桥体积V∗=V/Reff3，V—颗粒间液桥总体积；θ—固液接触角。

其中，液桥体积V的计算根据文献［10］的分析进行计算：

式中：Vi、Vj—颗粒i，j上的液桥体积；其中，液桥体积Vi，Vj计算如下式：

式中：ω—颗粒i的外在质量含水量；Mi—颗粒i的质量；ρl—颗粒间液体的密度；

2.2 液桥断裂判据

颗粒间及颗粒与筛板间的液桥会在两颗粒间距增大的时候拉伸，当表面间距大于某一特定值时液桥发生断裂，此时液桥断裂极限距离Scp与液桥体积和固液接触角有关。

对于两球形颗粒有：

对球形颗粒和平面有：

式中：scP—两球形颗粒间液桥断裂时的极限表面间距。

基于离散元法的液桥力接触模型计算原理，如图2所示。

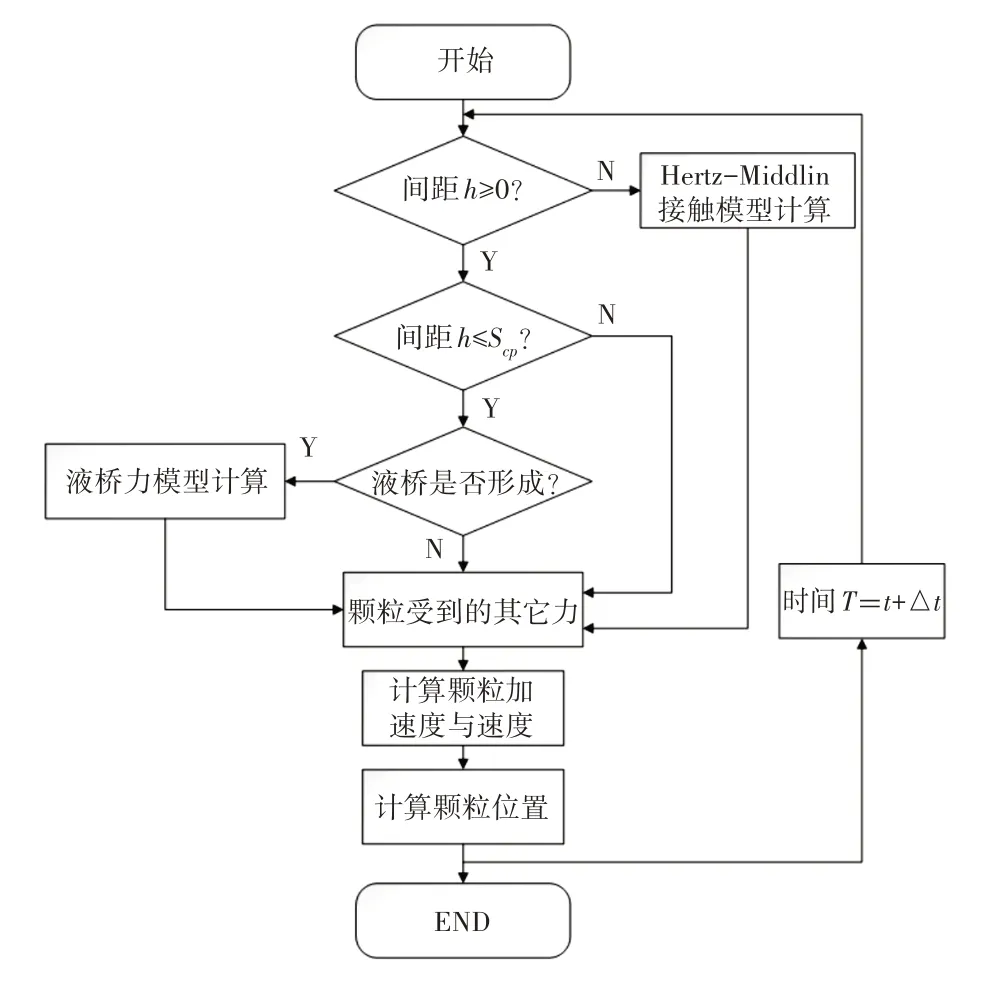
图2 液桥力接触模型计算原理Fig.2 Calculation Principle of Hydrobridge Force Contact Model

2.3 弛张筛原理

曲柄连杆式弛张筛的工作原理示意图，如图3所示。

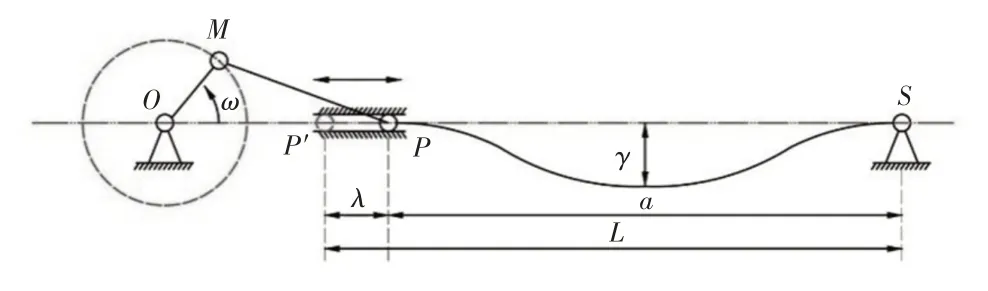
图3 弛张筛曲柄连杆模型Fig.3 Model of Flip-Flow Screen′s Crank-Guide Mechanism

图中：L—浮动筛框和固定筛框的最大间距；γ—筛面中点当前时刻扰度；a—两筛框瞬时的间距；λ—浮动筛框振幅，中心点O—浮动筛框的驱动轴；M点—偏心轴并与O点组成曲柄；P—浮动筛框；S—固定筛框。弛张筛在工作时，曲柄OM绕中心O以角速度ω进行旋转运动，从而带动浮动筛框P相对固定筛框S作往复运动，使得弛张筛筛板进行交错进行的弛张运动。根据原理图可得浮动筛框的速度为：

式中：v—浮动筛框的速度，m/s；ω—驱动轴的旋转角速度，rad/s；r—曲柄的偏心距，m；t—筛机开机时间，s；由上诉可知浮动端弛张偏心距为r且浮动端振幅为2r。

2.4 参数设置

针对弛张筛聚氨酯筛板的材料特性，使用Mooney-Rivilin两参数模型模拟弛张筛筛板的非线性扰曲运动，因此定义应变能密度函数中的两个系数coe（f1）=0.44 MPa，coe（f2）=1.76MPa。为模拟潮湿煤团聚体与柔性体弛张筛碰撞解聚的过程，弛张筛与团聚体煤颗粒的材料属性及接触参数设置，如表2、表3所示。

3 团聚体建模

3.1 团聚体粒径组成

为明确潮湿煤团聚体颗粒粒径组成，选取一定质量的干燥原煤，加水至外在质量含水量为10.5%，使煤和水混合均匀；然后在含水物料中借助工具挑取潮湿煤团聚体若干并使其整体尺寸尽量相近，如图4（a）所示。将潮湿煤聚团干燥处理，如图4（b）所示。将干燥后的聚团通过不同筛孔尺寸的套筛进行充分筛分，筛分数据，如表1所示。并通过排水法测得颗粒密度为1538kg/m3。取筛分粒径段内最大粒径尺寸作为建模参数，最终基于筛分数据得到聚团颗粒粒径组成为：

表1 材料特性Tab.1 Material Properties

表2 接触属性设置Tab.2 Contact Property Settings

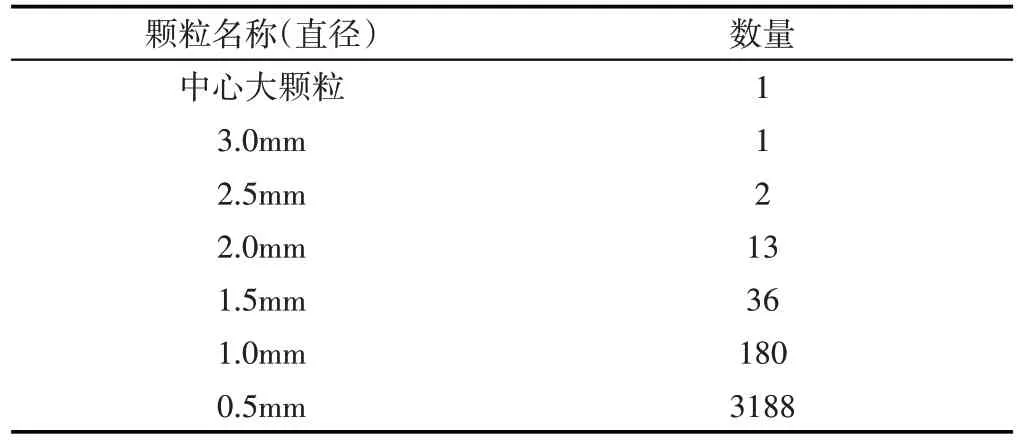
表3 团聚体颗粒粒径组成Tab.3 Composition of Aggregate Particle Size

图4 聚团建模过程Fig.4 Cluster Modeling Process

3.2 EDEM建模

充分筛分后，聚团的中心大颗粒与周围小颗粒透筛分离，测量20个中心大颗粒的质量，并选取一个质量接近20个大颗粒的平均质量的颗粒作为建模参考，其整体现状接近四面体，如图4（c）所示。利用EDEM的非球形颗粒建模功能，将若干尺寸相等且尺寸较大的球形颗粒通过相互重叠的结合形式组合形成中心非球形大颗粒，如图4（d）所示。此时小颗粒与中心大颗粒的接触近似替代为小球与大球的接触。

利用EDEM颗粒工厂功能生成湿煤聚团颗粒，各粒径数量按照实验所得数据（如表1所示）生成，通过两个半球壳体在一定速度下相对运动进行压制，如图4（e）所示。最后结合液桥力接触模型生成基于EDEM软球模型的湿煤聚团模型，如图4（f）所示。

4 EDEM-RecurDyn联合模拟

4.1 碰撞解聚对比分析

为分析湿煤聚团与弛张筛筛板的碰撞解聚过程，以及弛张运动筛板对团聚体碰撞解聚的作用机理，弛张筛板设置驱动转速为n=600r/min，张紧量为Ex=0mm，倾斜角为α=0°，偏心距为e=5.5mm。对液桥力接触模型（假设液体分布均匀），设置液桥生成时间t≥0s，颗粒间液体密度ρ=1000kg/m3，固液接触角θ=30°。分别设置团聚体以初速度为1500mm/s与静止筛板碰撞、团聚体以初速度1500mm/s与弛张运动筛板碰撞，两种情况下，碰撞过程中的团聚体颗粒速度分布（颗粒以速度表矢量表示且矢量大小代表颗粒大小，即矢量标识越大代表颗粒越大，颜色代表速度大小），如图5所示。

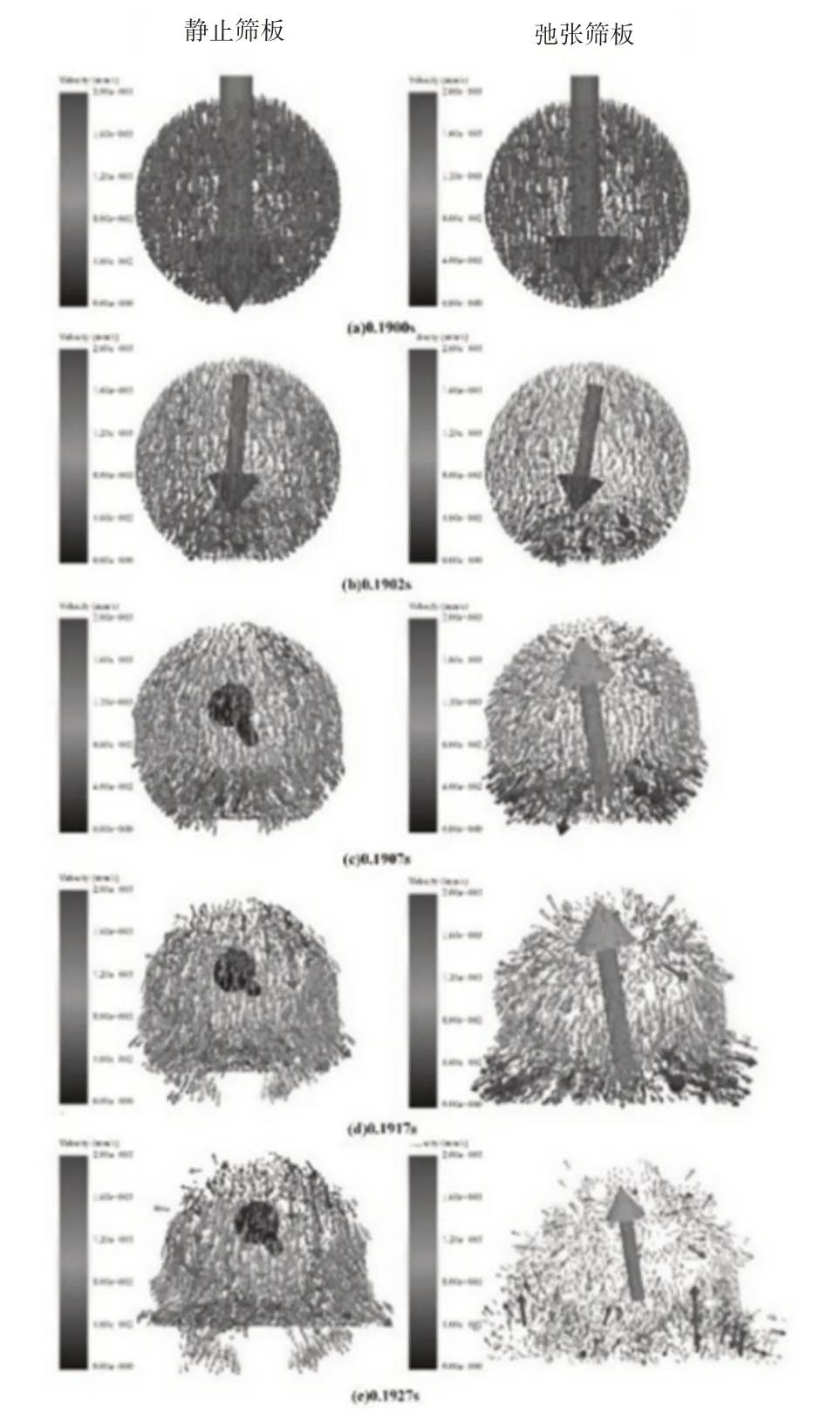
图5 碰撞解聚过程及速度分布Fig.5 Collision Depolymerization Process and Velocity Distribution

为表征碰撞过程中湿煤聚团的解聚程度，定义聚团液桥断裂程度系数k，其计算方法为：

液桥的状态由颗粒接触半径、液桥极限断裂距以及颗粒间距决定，由式（10）可知，k≥0时聚团发生解聚，且k的值越大代表聚团内颗粒间液桥的断裂程度越大，即聚团解聚程度越大。设置团聚体以初速度为1500mm/s 与静止筛板碰撞、团聚体以初速度1500mm/s与弛张运动筛板碰撞（此时筛面最大速度为1246mm/s）、团聚体以初速度为2746mm/s与静止筛板碰撞；三种情况下，聚团的解聚程度，如图6所示。

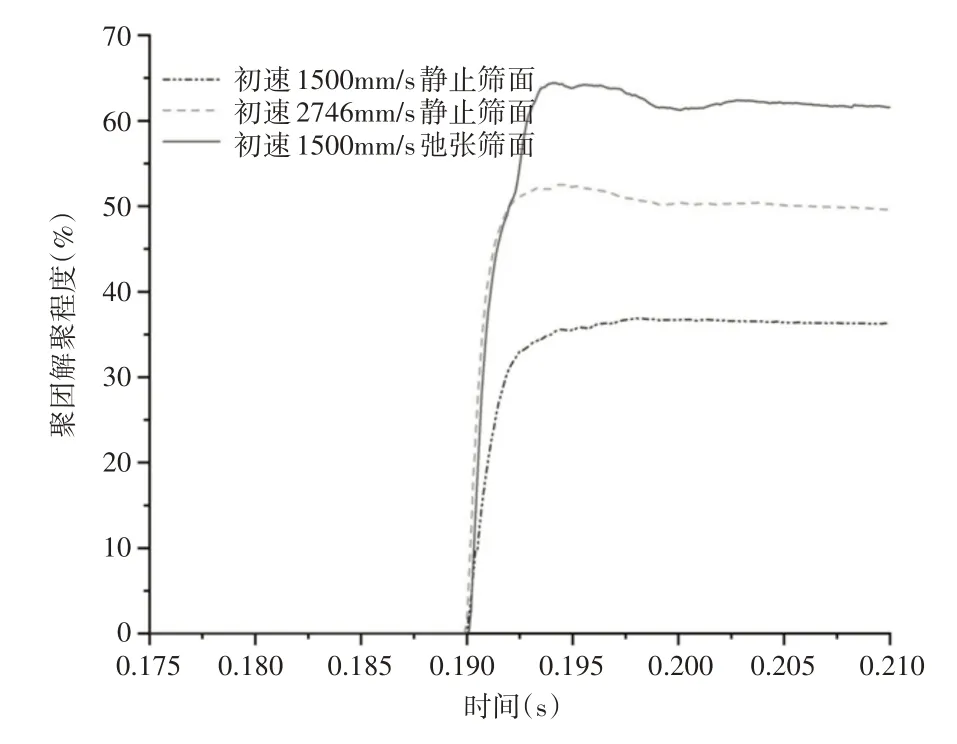
图6 解聚程度对比Fig.6 Comparison of Depolymerization Degree

由图5、图6可知，聚团和筛板接触之前，聚团颗粒具有一致的速度大小与方向，此时聚团处于稳定状态。湿煤聚团和弛张筛筛板的碰撞解聚过程可以大体上分为三个阶段：开始解聚阶段、快速解聚阶段、趋于稳定状态。

在开始解聚阶段，如图5（a）、图5（b）所示。聚团与筛板开始接触发生碰撞，接触点附近的颗粒受到较大的接触力，造成其速度方向改变为向四周扩散且速度大小与方向发生变化，此时该区域内的颗粒间产生碰撞，使接触区域内颗粒间的液桥粘结发生断裂，聚团开始发生解聚，同时中心大颗粒受到较大的接触力而发生速度的改变，但是此时上部区域的大部分速度依然保持相对稳定。

随着聚团颗粒与筛板相对距离的进一步减小，当颗粒间的碰撞通过中心大颗粒传递至聚团中部和上部时，如图5（c）、图5（d）所示。区域内大量颗粒受到较大的接触力而发生明显的速度改变，此时聚团解聚程度快速增大，聚团解聚进入快速解聚阶段。在快速解聚阶段，聚团中部四周的一部分颗粒依然向下运动，挤压在下部分向四周运动的颗粒，引起下部分小颗粒群发生透筛和进一步的速度改变。快速解聚阶段是聚团与筛板碰撞发生解聚和透筛的主要阶段。当颗粒整体向上和四周运动的时，聚团解散为中心大颗粒与少部分小颗粒、小颗粒间形成的二级小聚团，此时颗粒的速度与力整体相对平衡，聚团的解聚过程趋于稳定。

相对筛板处于静止状态，筛板处于弛张状态时，由于筛面具备一个较高的速度，这使得聚团与筛板碰撞后，颗粒受到更大的接触力且具有更大的速度，使得颗粒间距增大，液桥断裂数量增加；因此，聚团在和弛张筛板碰撞的情况下，获得了更大的解聚程度和更快的解聚速度，如图6所示。

筛板对聚团解聚程度的增强作用不仅仅因为筛面速度的增加，如图6所示。当将弛张筛筛板与聚团碰撞时的最大速度施加在聚团时，聚团与筛板碰撞的解聚程度依然小于聚团与弛张筛板碰撞，这是因为弛张运动的聚氨酯筛板具有较大速度的同时，带有筛孔的筛板发生向上的弹性扰曲运动对聚团有碰撞切割作用，这有效的增强了聚团的碰撞解聚。

4.2 筛板弛张偏心距对团聚体解聚的影响

偏心距是曲柄连杆式弛张筛工作的关键参数之一，因此研究偏心距对聚团与弛张筛筛板碰撞解聚的影响，能为曲柄连杆式弛张筛的结构参数优化提供一定的参考依据。偏心距的改变首先会影响筛面的形变，不同偏心距对筛面最大扰度和转角的影响，如图7所示。由图7可知，偏心距的增加会增大筛面的最大扰度和转角，进而会增大筛板发生兜矿的风险，进而会对筛分造成不利的影响；因此，偏心距的取值应在合理范围内。

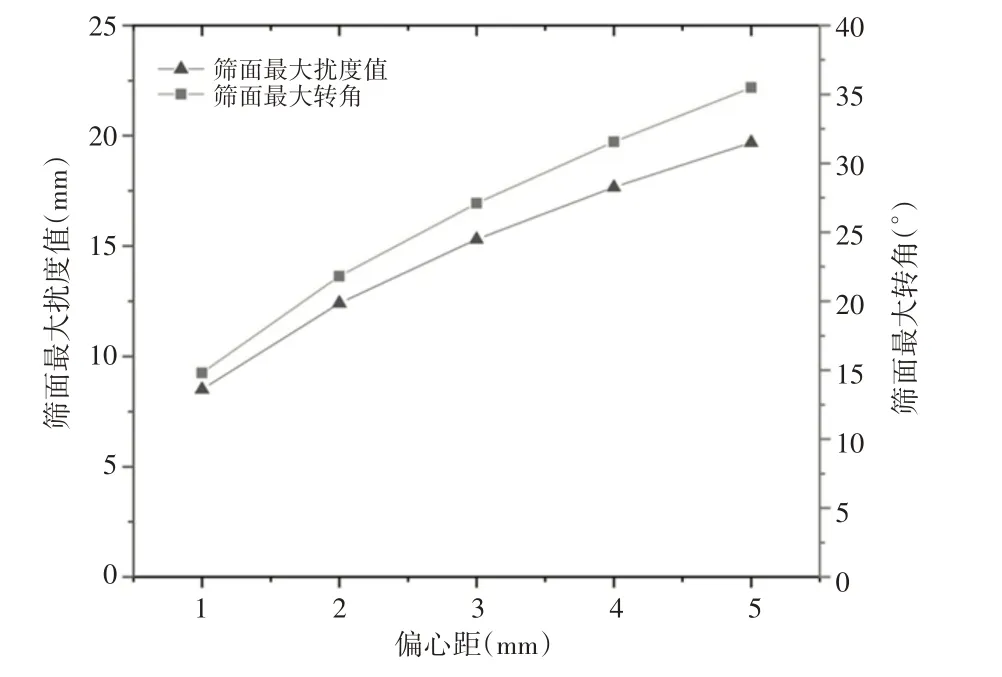
图7 偏心距对筛板形变的影响Fig.7 The Influence of Eccentricity on the Deformation of Sieve Plate

为分析偏心距数值变化对聚团解聚的影响，设置筛板倾斜角15°，转速550r/min，偏心距分别为1mm，2mm，3mm，4mm，5mm，聚团以相同初速度和相同高度释放与不同偏心距的弛张筛筛板碰撞。碰撞情况，如图8所示。

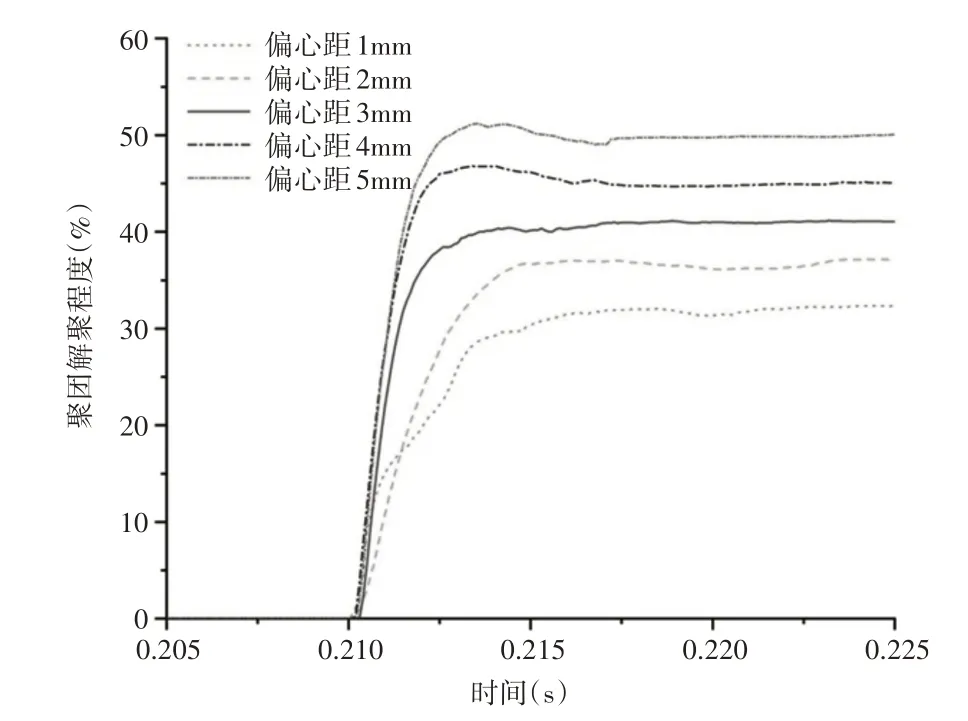
图8 偏心距对团聚体解聚的影响Fig.8 The Influence of Offsets on Aggregate Depolymerization

由图8可知，聚团的解聚依然经历了开始解聚、快速解聚、趋于稳定三个阶段。增大弛张筛的偏心距能有效增大湿煤聚团和弛张筛筛板碰撞的解聚程度和解聚速度。因为增大筛板的偏心距能增大筛面的速度与加速度，进而增大了碰撞过程中聚团颗粒受到的接触力和颗粒速度，使得聚团颗粒间距和液桥断裂数量增大，从而使得聚团解聚程度增大。

综合图7、图8可知，并不能无限制的增大偏心距以增大筛板对湿煤聚团的打散作用，应在合理的取值范围内增大偏心距的值以获得更大的聚团解聚程度，以避免发生兜矿现象对筛分造成负面影响。

5 结论

（1）基于聚团筛分实验数据和液桥力接触模型构建模拟真实情况的中心非球形大颗粒与周围非等径小颗粒粘结而成的湿煤聚团模型，通过建立EDEM-RecurDyn联合模拟分析了湿煤聚团与柔性体弛张筛筛板的碰撞解聚行为，对比分析了湿煤聚团与静止筛板和弛张筛板的碰撞解聚过程。

湿煤聚团和弛张筛筛板的碰撞解聚过程大致可以分为三个阶段：开始解聚、快速解聚、趋于稳定状态。

湿煤聚团与弛张筛筛板的碰撞解聚首先发生在聚团与筛面的接触区域，随后聚团颗粒间的碰撞通过中心大颗粒传递至聚团中部和上部，引起聚团的快速解聚，同时部分中部的颗粒向下运动造成下部颗粒的透筛运动，随后颗粒整体向上和四周运动，解聚过程趋于稳定；

（2）相比静止筛板，弛张运动的筛板对与聚团发生碰撞时，聚团颗粒受到更大的接触力且具有更大的速度，这能有效增加液桥断裂数量，聚团因此获得更大的解聚程度和解聚速度。

（3）保证不发生兜矿的情况下，在合理取值范围内，增大偏心距能有效增大聚团与筛板碰撞时聚团的解聚程度和解聚速度。

（4）这里仅就弛张筛偏心距这单一因素对聚团碰撞解聚的影响进行了联合模拟分析，该结论为曲柄连杆式弛张筛进一步的优化设计提供一定的参考依据。