螺栓连接随机振动下的疲劳分析

刘召辉，项继圣，孙清超，穆晓凯

（1.大连理工大学机械工程学院，辽宁 大连 116024；2.襄阳航力机电技术发展有限公司，湖北 襄阳 441052）

1 引言

随着社会发展，电机在许多领域得到应用，同时电机控制器是电机的重要组成部分，电机在工作过程中其内部的转子高速转动，对电机控制器造成了影响。由于电机控制器的螺栓连接结构采用较大长径比的螺栓连接，在振动工况下螺栓振幅较大，进而结构容易产生疲劳损伤现象。

振动造成的疲劳失效已经成为疲劳领域的一个热点问题［1-3］，由振动载荷造成的疲劳破坏主要有3种：（1）由于结构产生共振现象进而造成结构的疲劳破坏；（2）结构振动的最大响应超过了危险阈值而造成的破坏；（3）由结构振动累计损伤造成的疲劳破坏。由于振动疲劳涉及结构动力学问题，对其解释尚未形成理想的统一，但是在各种结构设计手册或设计规范中对振动疲劳都有详细的规定［4-6］。在电机控制器结构设计工作中，螺栓连接通常以静强度为准则，然而实际上，周期动载荷造成连接结构疲劳破坏，甚至断裂。

在许多领域中存在随机振动疲劳问题，电子设备体积小、结构精密，振动对其影响较大，文献［7］对某电子设备采用随机振动PSD分析法进行仿真，仿真结果的关键危险位置与实际结果相一致，但只有量级参考价值，无法精准地预测疲劳寿命；压缩机中的冷凝器常出现振动疲劳，文献［8］提出了一种冷凝器支架优化模型，可以优化冷凝器支架在随机振动过程中的疲劳损伤，但没有进行理论计算，缺少理论验证；机械结构振动过程中常伴有温度变化，文献［9］通过热循环载荷和随机振动载荷的耦合，分析了电路板的疲劳寿命，发现焊点失效主要原因为热循环载荷，引线故障主要原因为振动载荷，但由于结构没有得到优化，因此在一定程度上具有主观性。

此外，随机振动疲劳问题较为复杂，为便于计算且提高计算准确性，文献［10］提出了基于PSD的随机振动设计寿命计算公式，计算了构件的设计寿命；文献［11］提出了基于频域随机振动载荷结构疲劳寿命计算方法，对疲劳寿命计算公式进行了修正；工程中常通过nCode软件仿真计算结构疲劳寿命，文献［12］对某机载单元进行随机振动疲劳分析，验证了利用此软件对结构的随机振动疲劳寿命进行分析的可行性，但没有通过试验进行验证，缺乏一定的可靠性；文献［13］研究了五种疲劳分析的频域算法，据此提出了基于频域算法的结构随机振动疲劳的加速试验计算方法，但其设置的S-N曲线为手册当中查找得到，未对实际材料进行试验计算S-N曲线，该设计方法结果与试验结果存在一定误差；文献［14］根据频率分析方法，对结构进行振动疲劳分析，验证了利用共振频段载荷谱代替整谱的有效性，但并未考虑实际情况中的温度等因素，使计算结果与试验结构有较大误差。文献［15］通过随机振动仿真计算工程车辆驾驶室固有振动模态与累计损伤，验证了仿真方法计算驾驶室结构疲劳寿命的可行性。

针对目前设计工作中，螺栓连接大多依靠静刚度为设计准则，计算结果对实际设计工作参考价值不大的情况，利用Miner线性累计损伤理论与随机振动仿真方法分析某电机控制器螺栓连接的随机振动疲劳破坏，分别计算该结构的疲劳损伤值与疲劳寿命值，发现原有结构疲劳寿命不满足实际工况，对原有结构进行改进，减小了螺栓的长径比。计算了Miner理论结果与仿真结果的误差，验证了Miner线性累计损伤理论对螺栓连接随机振动的准确性。

最后通过对螺栓连接结构进行理论、仿真计算与随机振动试验，结果表明改进后的结构提高了随机振动疲劳寿命，验证了改进后结构的可靠性。

2 随机振动疲劳理论分析

计算结构在随机振动工况下的疲劳使用寿命主要依据疲劳损伤累计理论，该理论假定结构在不同的循环应力作用下的疲劳损伤是线性叠加的，是在一定程度上发生在结构某处的疲劳损伤。根据Miner所提出的线性累计损伤理论，其在应力分布连续的状态下的叠加损伤值可以表示为：

式中：Ns—当疲劳寿命曲线S-N曲线上应力值为s时，导致疲劳破坏的循环次数；ns—在载荷对应的应力值为s时，加载时间为t的实际作用次数。

式中：E(p)—随机响应信号峰值频率的期望值；T—随机响应的激励时间；PP(s)—概率密度函数，用来表征ns；b、C—结构材料特性的S-N曲线常数。

将式（2）、式（3）代入式（1）中得：

当D<1时，结构安全，当D>1时，结构位置会发生疲劳破坏。一般情况下，采用上式计算结构在随机振动工况下的疲劳寿命可以满足要求，但是求解过程较为繁琐，不适用于工程计算，因此本文通过Steinberg提出的综合Gauss 分布及Miner线性累计损伤理论的三区间法，将疲劳损伤计算公式进行了简化，Gauss分布的应力三区间，如图1所示。应力分布在各区间的概率，如表1所示。

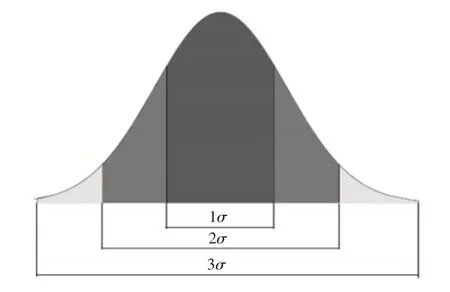
图1 3σ区间示意图Fig.1 Schematic Diagram of 3 Interval

由上表可知，随机振动过程中结构产生大于3σ的应力仅有0.27%的概率，并假定在此概率下产的应力不会对结构造成任何损伤，则简化后的式为：

结构失效前疲劳寿命计算公式为：

式中：n1σ—振动的实际循环次数小于或等于1σ（0.68）；n2σ—振动的实际循环次数小于或等于2σ（0.271）；n3σ—振动的实际循环次数小于或等于3σ（0.0433）；1σ，2σ，3σ应力水平分别对应的应力可循环次数由手册中的S-N曲线查得，并表示为N1σ,N2σ,N3σ;—随机应力以正斜率通过均值μ的平均频率；mn—G(f)的N阶惯性矩；G(f)-频率f处的单边PSD。

3 电机控制器螺栓连接结构随机振动疲劳分析

随机振动疲劳分析是分析在随机激励下结构的振动疲劳失效情况。电机控制器的主要力学环境是随机振动，随着耐久要求越来越高，随机振动疲劳失效成为重点研究对象。为便于实际工程计算，分别三区间法进行理论计算和Workbench仿真计算结构疲劳损伤和疲劳寿命。仿真时输入随机激励PSD-G曲线，仿真计算得知结构的等效应力，三区间法理论计算建立在得知应力大小基础上，同时进行疲劳寿命与疲劳损伤计算，将三区间理论计算值与疲劳仿真结果比较，验证理论方法的可行性。

为保证有限元计算结果可靠并简化有限元计算，考虑在不影响计算结果的前提下，利用SolidWorks三维建模软件对电机控制器底座、螺栓连接结构、质量块等简化后进行三维建模，简化后模型，如图2所示。

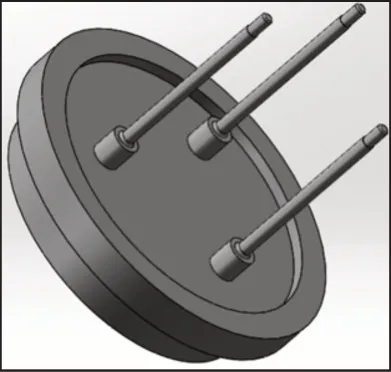
图2 简化后模型Fig.2 Simplified Model

分析流程图，如图3所示。基于Workbench对某电机控制器螺栓连接结构进行随机振动疲劳分析，建立有限元分析模型，输入PSD-G曲线，根据等效应力查看并计算危险位置及随机振动疲劳损伤值与寿命值；在此基础上进行随机振动疲劳仿真分析，将结果与计算值进行比较，分析结果是否符合要求，若不满足需求，则对螺栓连接结构改进后重复上述步骤，若满足需求则完成分析，其中Workbench流程图，如图4所示。

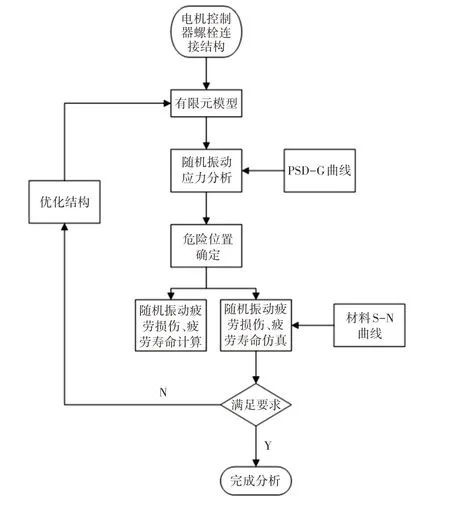
图3 随机振动载荷下寿命预测分析流程图Fig.3 Flow Chart of Life Prediction Under Random Vibration Load

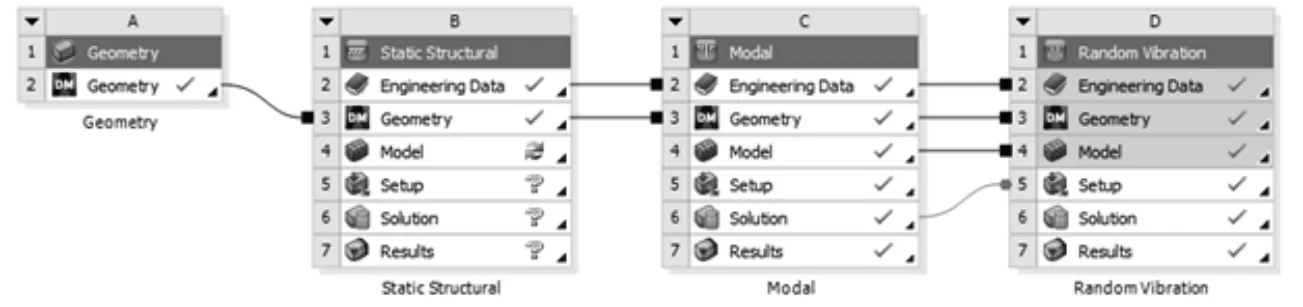
图4 Workbench随机振动疲劳分析Fig.4 Workbench Random Vibration Fatigue Analysis

3.1 随机振动应力仿真分析

电机控制器螺栓连接结构底座材料为ZL101A，螺栓材料为1Cr17Ni2，在“Engineering Data”中添加所需材料属性，材料各参数，如表2所示。

表2 电机控制器螺栓连接结构各部件材料属性Tab.2 Material Properties of Bolt Connection Structure of Motor Controller

在Workbench 中设置1Cr17Ni2 材料的S-N 曲线，横坐标为发生疲劳破坏时的可循环次数N的对数，纵坐标为对应交变应力S的对数，如图5所示。

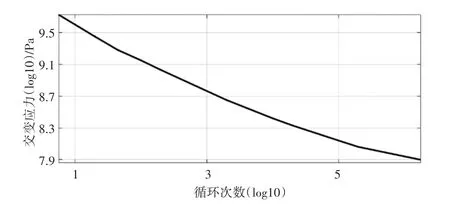
图5 1Cr17Ni2材料S-N曲线Fig.5 The S-N Curve of 1Cr17Ni2 Material

有限元计算中，划分模型网格的方法以及划分后的网格单元、网格结点数会影响仿真计算的精度与速度，在保证仿真计算结果的精度与速度的前提下，将网格进行规整化及细化，根据结构复杂度，将底座设为六面体网格，螺栓设为四面体网格，底座网格大小设置为1mm，螺栓设置为0.5mm，划分后有267401 个结点，99503个单元。

实际工况中电机控制器螺栓连接结构需承载一定的质量，在仿真中将承载质量平均分配给螺栓，分别对三根螺栓添加分布质量，对电机控制器螺栓连接结构底座添加“Fix support”约束，其他位置不添加约束，确保与实际情况相符，随机激励PSD-G曲线，如图6所示。

应力分析使用应力安全系数评估结构可靠性。应力安全系数Sf计算公式如下：

式中：σs—材料的屈服强度；rm—材料的安全系数；σv—螺栓的最大等效应力。此处材料安全系数取1.1。

根据电机控制器螺栓连接结构工作环境环境，应用该电机控制器在实际工况下的随机振动PSD-G曲线，仿真计算应力结果，如图7 所示。根据图中应力分布结果可知，最大等效应力为756.02MPa，并通过式10计算得安全系数为0.887，且轴径变化圆角处产生了最大等效应力，周围应力梯度大，变化明显，可以判断该结构在此处产生应力集中现象。

图7 等效应力图Fig.7 Equivalent Stress Diagram

根据材料1Cr17Ni2的S-N 曲线及最大等效应力可知，应力赋值为1σ=252.01MPa 时，对应的疲劳寿命N1σ=1159；应力赋值为2σ=504.01MPa 时，对应疲劳寿命N2σ=113；应力赋值为3σ=756.02MPa时，对应疲劳寿命N3σ=39；将结果代入式（5）可得结构疲劳损伤为：

由式（8）、式（9）计算随机振动疲劳寿命为：

由此可知，根据等效应力计算的随机振动疲劳寿命结果表明结构可循环次数较低且可持续实验时间较短，结构需要改进。

3.2 随机振动疲劳仿真分析

在等效应力计算结果的基础上，进行疲劳寿命与疲劳损伤计算，计算结果，如图8所示。可得最小疲劳寿命值为275.31，可判断结构不能达到疲劳寿命要求。

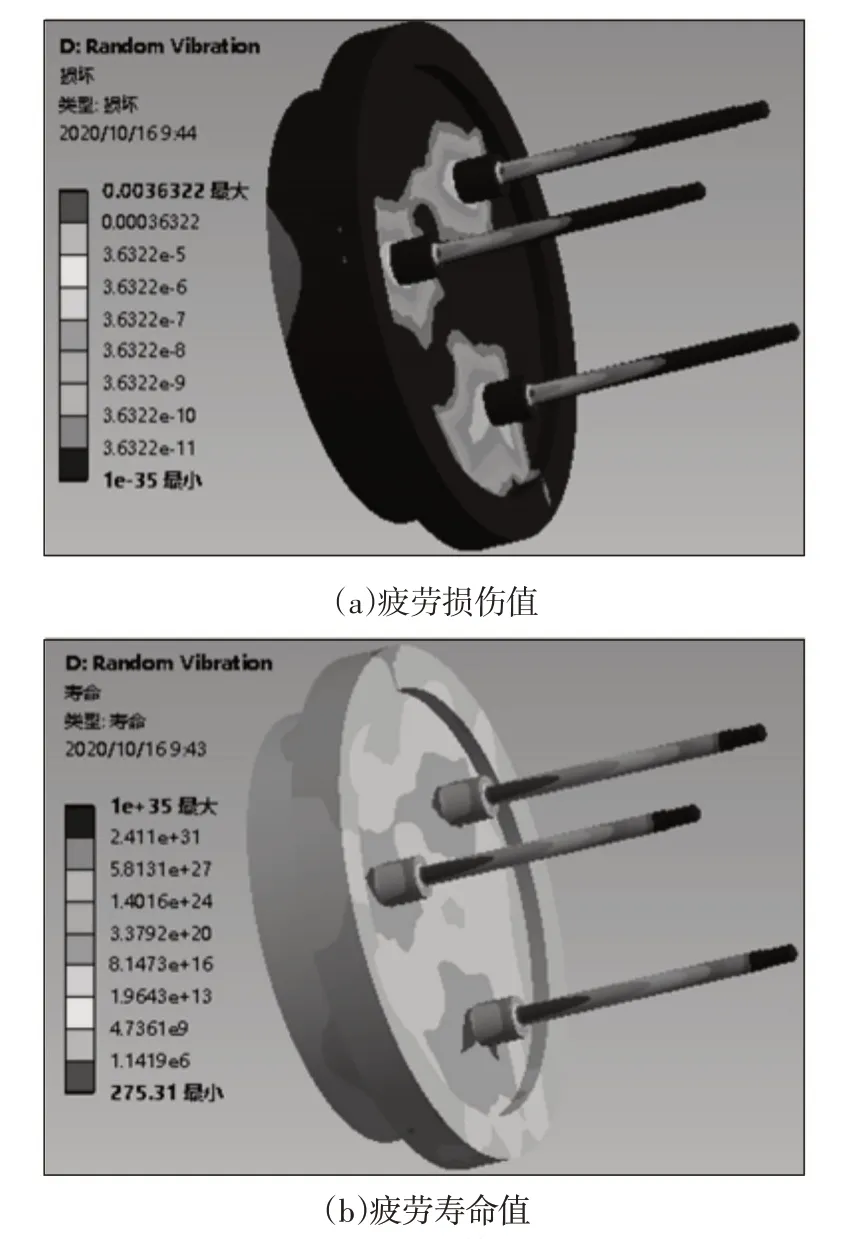
图8 疲劳计算结果Fig.8 Fatigue Calculation Result

上述根据等效应力计算随机振动疲劳结果与仿真结果具体数值并不相同，主要为计算时材料S-N曲线取值差异，疲劳损伤差为4.86%，疲劳寿命差为5.28%，如表3所示。但定性分析结果一致，当前结构无法满足实验需求，需对其进行改进。

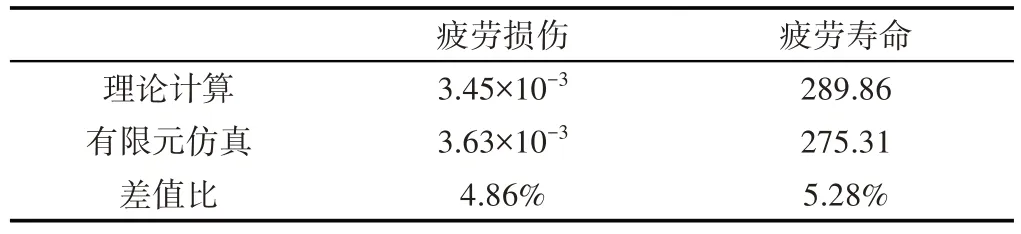
表3 理论分析与有限元仿真结果对比Tab.3 Comparison of Theoretical Analysis and Finite Element Simulation Results

表4 电机外盒材料参数Tab.4 Material Parameters of Motor Outer Box

4 模型改进与分析

由图7、图8可知，螺栓在轴径变化处出现明显的应力集中现象，且疲劳寿命非常低。为使螺栓结构轴径变化处的应力集中对螺栓结构的疲劳寿命影响降低，需对结构进行改进，主要措施为降低螺栓长径比，将三根螺栓改为六根螺栓，并添加一铝合金外壳，如图9所示。铝合金铸造外壳材料为2A70-T6，具体材料参数，如表3所示。

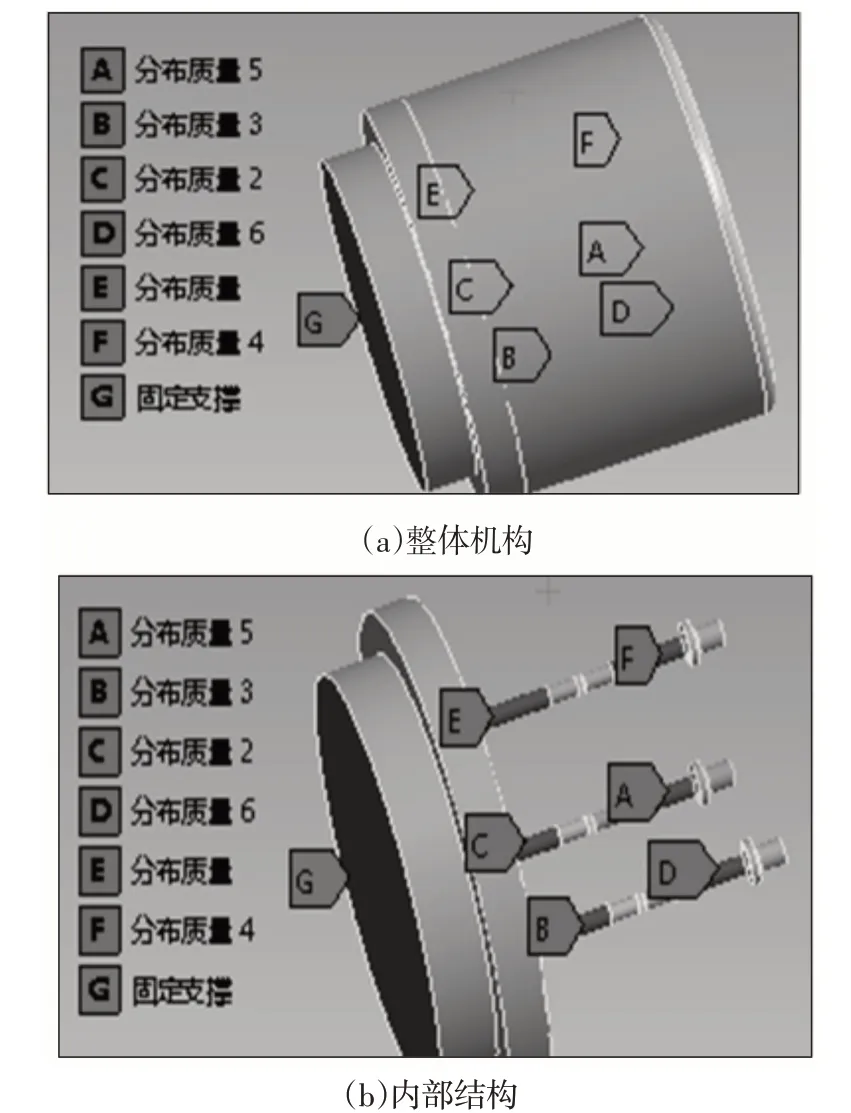
图9 改进后的结构Fig.9 The Improved Structure

4.1 随机振动等效应力仿真分析

为保证模型改进后的数据正确与有效性，按同样的方式对结构进行网格划分、边界条件及功率谱（PSD-G）加载设置。模型改进后长径比减小，因此会影响等效应力的大小，进而影响结构的疲劳寿命，等效应力仿真结果，如图10所示。由图中可知最大等效应力为101.73MPa，通过应力安全系数计算公式得其安全系数为6.75。出现应力集中的位置仍为轴径变化圆角处，但可以发现应力值和应力梯度减小，应力集中现象明显降低，同时安全系数显著增大。

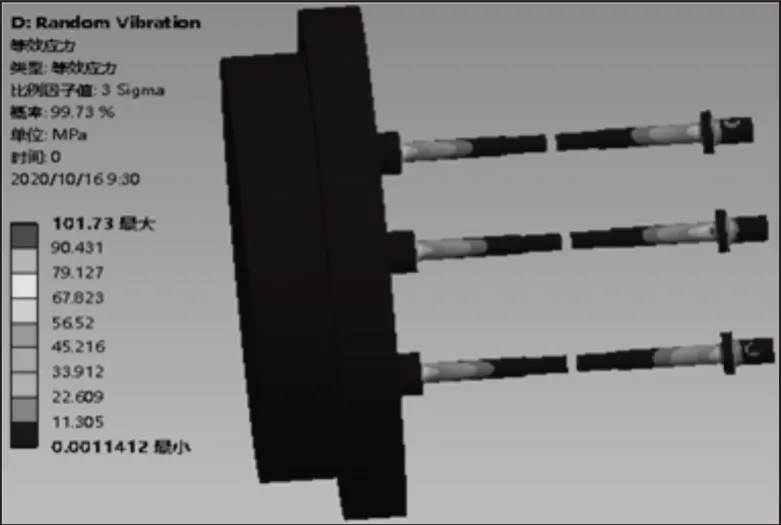
图10 结构改进后等效应力图Fig.10 Equivalent Stress Diagram of Improved Structure

根据材料1Cr17Ni2的S-N 曲线以及最大等效应力可知，应力赋值为1σ=33.91MPa时，对应的疲劳寿命N1σ=4 469000；应力赋值为2σ=67.82MPa时，对应疲劳寿命N2σ=+∞；应力赋值为3σ=101.73MPa时，对应疲劳寿命N3σ=+∞；将结果代入式（5）可得结构疲劳损伤为：

由式（8）、式（9）计算随机振动疲劳寿命为：

由上述计算结果可知，疲劳破坏很小，仅为10-7量级，疲劳可循环次数为106，实验时间可达1815.5h，满足实际需求。

4.2 疲劳仿真分析

结构改进后的疲劳仿真结果，如图11所示。结构改进后最大疲劳损伤为1.34×10-7，最小寿命为7.48×106，计算得Tf=2077.8h，显著提高了结构的疲劳寿命。

图11 结构改进后疲劳寿命图Fig.11 Fatigue Life Diagram of Improved Structure

与4.1节中根据等效应力计算的随机振动疲劳结果对比，发现计算结果较仿真结果稍小一些，主要原因为对材料S-N曲线的取值并不完全相同，最终疲劳损伤差为5.22%，疲劳寿命差为5.21%，如表5所示。定性分析可得结构改进满足实际需求。

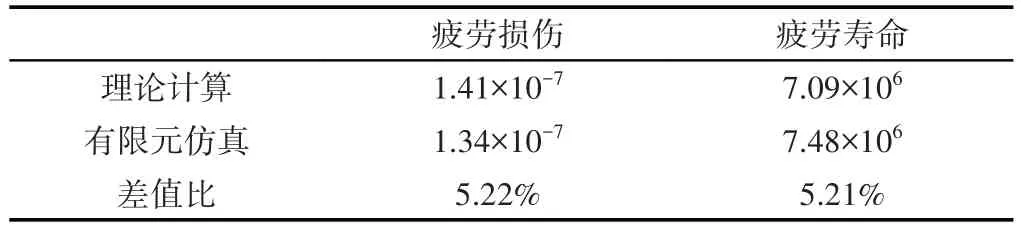
表5 理论分析与有限元仿真结果对比Tab.5 Comparison of Theoretical Analysis and Finite Element Simulation Results

5 随机振动试验

对改进前后的结构制作样件，螺栓大小为M3，采用相应的夹具将设备固定在振动台上，振动试验台型号为SA30-T1000-58F/ST，如图12（a）所示。分别对X、Y、Z三个方向进行功能振动1h、耐久振动1h，振动激励与仿真激励图6相同，分别记录结构改进前后的断裂情况，如表6所示。

表6 结构改进前后实验结果对比Tab.6 Comparison of Experimental Results Before and After Structural Improvement

图12 螺栓试验图Fig.12 Bolt Test Chart

结构改进前振动结果为螺栓圆角处发生断裂，与Steinberg理论计算和仿真结果吻合，如图12（b）所示。螺栓断裂的主要原因为螺栓长径比较大，圆角处应力集中严重，因此此设备结构有安全隐患，需要对结构优化改进，减小螺栓长径比。结构改进后对其进行与上述条件相同的振动试验，发现螺栓圆角处没有发生疲劳破坏，通过了随机振动试验，如图12（c）所示。验证设备结构改进后的可靠性与理论、仿真计算的可行性。

6 结论

这里采用Steinberg提出的三区间法和Workbench有限元仿真分析，对某电机控制器螺栓连接结构在随机振动过程中螺栓发生断裂进行了研究，主要完成的工作与结论如下：

（1）基于Steinberg提出的三区间法，计算了某电机控制器螺栓连接结构疲劳寿命值，并分析螺栓连接结构发生疲劳破坏的主要原因为应力集中，最后通过Workbench仿真计算螺栓连接结构疲劳寿命，与三区间法计算值相差5.28%，验证了三区间法对螺栓连接随机振动的准确性。

（2）针对结构不满足疲劳寿命要求，对结构进行改进，减小了螺栓长径比，基于Steinberg提出的三区间法与随机振动仿真计算改进后的螺栓连接结构疲劳损伤与疲劳寿命，改进后的结构疲劳寿命提高了1011倍，验证了结构改进的可靠性。

（3）利用随机振动实验台，对改进前、改进后的螺栓连接结构进行试验，所得结果与采用Steinberg提出的三区间法和仿真计算结果吻合较好。因此，利用这里方法对螺栓连接结构进行随机振动疲劳分析是可靠的，对其他机械结构计算随机振动疲劳寿命提供了借鉴依据。