参数优化设计与TRIZ理论集成设计方法研究

刘 尚，郭霄霞，韩 刚，王红艳

（齐齐哈尔大学机电工程学院，黑龙江 齐齐哈尔 161006）

1 引言

概念设计处于产品设计的早期，是新产品研发的关键环节。这一环节面临着复杂的用户需求并对产品整个设计过程具有深远影响［1］。

如何获得可行解，是这一环节中的一个至关重要的问题［2］。概念解中存在着设计冲突或设计缺陷等设计问题，是影响其可行性的重要因素。

应用TRIZ理论来解决这些设计问题，是提高概念解可行性的有效方法。这就需要首先要准确地捕捉到设计问题。

将TRIZ理论与QFD和公理化设计等理论方法结合应用，是捕捉设计问题最常用的方法。前者，用QFD来发现“做什么”，用TRIZ来解决“怎样做”［3-4］。后者，用TRIZ理论解决公理化设计流程中的设计耦合问题［5］。

上述方法能够从概念设计的角度发现设计问题并交给TRIZ求解，但无法发现隐藏在具体设计中的冲突或者缺陷。

通过分析仿真数据来发现设计问题，并交给TRIZ求解被验证是一种有效的方法。文献［6］提出将系统动态仿真与物场分析结合的方法，并将其应用于求解马克笔的设计问题。文献［7］提出将CAD软件与TRIZ理论结合，应用CATIA软件完成剪式举升装置结构建模，采用ABAQUS进行有限元分析，然后通过仿真数据提炼问题并转化为TRIZ问题模型来求解。文献［8］将遗传算法与TRIZ理论结合应用于橙子的包装箱设计。上述分别从概念设计和具体化设计阶段捕捉设计问题，并交给TRIZ产生新概念解，构成了设计的迭代过程。

文献［9］指出TRIZ 所提供的策略解向领域解转化时，需要根据具体的问题情景尽可能的减少新资源的引入。参数优化设计是解决具体化设计阶段的设计冲突的有效方法，不需要引入新类型的资源。与TRIZ 理论比较，参数优化设计对系统改动更小。这就引出一个问题：面对具体化设计阶段发现的隐含于概念解中的设计冲突，应该选择TRIZ还是选择参数优化设计方法？

这里提出将参数优化设计与TRIZ理论相结合，来支持具体化设计阶段设计冲突问题的求解，来改善因该概念设计阶段参在设计冲突而影响解的可行性的问题。

2 优化设计冲突的表达及求解

2.1 优化设计冲突问题的分类及冲突的特点

参数优化设计是不改变原理结构的前提下，应用数值计算方法对设计变量之间取值冲突在可行域之内进行折中处理，来获得优化设计的数值最优解。尽管其对设计变量之间的冲突的处理方式与TRIZ理论所采用的凸显并消除冲突的处理方式相反，但其问题描述方式却可用于辅助TRIZ理论问题的定义以及领域解的转化。

式（1）所示将单目标函数通过线性组合表达为优化设计的数学模型。

式中：X=[x1，x2，L，xp]T—设计变量；F(X)—多目标函数的组合；fi(X)—某单目标函数；ωi—目标函数fi(X)的权重，gj(X)≤0—不等式约束条件；hk(X)=0—等式约束条件。

根据设计变量中x的数量，可将优化设计问题分为一维优化设计问题（p=1）和多维优化设计问题（p>1）。按照目标函数的数量可将优化设计问题分为单目标函数优化问题（n=1）和多目标函数优化问题（n>1）。根据设计变量维数和目标函数数量的组合，可将优化设计问题分为一维单目标优化设计问题，一维多目标优化设计问题，多维单目标优化设计问题和多维多目标优化设计问题。这四种类型与TRIZ理论问题表达之间的关系如下：

类型I：一维单目标优化问题。这类问题需要从优化设计目标和约束条件之间来分析和提取技术冲突关系，并分析设计变量取值上是否存在的物理冲突。

类型II：一维多目标函数优化问题。以每一个独立优化目标作为设计期望，研究各个设计期望之间以及设计期望与约束条件之间的冲突关系。将冲突按照设计变量取值分组，来提炼设计变量取值的不同需求，从而构建技术冲突与物理冲突之间的因果关系。这类问题往往会在同一设计变量上出现的物理冲突与多个技术冲突构成因果关系的情况。

类型III：多维单目标函数优化问题。这类问题需要从优化设计目标和约束条件中分析和提取技术冲突，并考虑设计变量取值上是否成物理冲突。这类问题往往会产生不同设计变量上的物理冲突，与同一个技术冲突构成因果关系的情况。

类型IV：多维多目标函数优化问题。这种类型比较复杂，需要以每一个独立优化设计目标作为设计期望，考虑各个设计期望、约束条件之间的冲突关系。同时，需要分析各类冲突与设计变量取值的物理冲突之间构成的因果关系。这类问题会构成由技术冲突和物理冲突构成的冲突网络。

对于难以显示表达的目标函数，可通过实验设计构建响应面实现优化设计，并从数据设计变量与目标函数以及约束条件的正负相关关系中提炼冲突。

2.2 优化设计冲突问题的表达方法

由于目标函数、约束条件等彼此之间的关系比较复杂，从优化设计数学模型向TRIZ冲突问题模型转化，往往会构成复杂的多冲突关联，仅仅用对单一冲突的表达和求解方法不能将冲突关系表达清楚，需要一种表达方法支持，这里提出基于ENV模型的冲突表达方法。ENV（Elements-Name of the Feature Value）模型是OTSM-TRIZ的重要内容，能够通过设计参数和评价参数之间的关系来表达技术冲突和物理重冲突［10-11］。而且，以ENV 模型为基础，可以表达多个评价参数和设计变量之间的多冲突并存的复杂冲突关系［12］。根据前文中优化设计冲突问题的分类及特点，将转化分为一维优化设计问题的转化和多维优化设计问题的转化。

2.2.1 一维优化设计问题的转化

一维优化问题仅存一个设计变量，冲突表达方法，如图1所示。其中，目标函数1和目标函数2泛指多目标优化中任意两个独立目标函数。在定义技术冲突的时候，需要考虑目标函数1与目标函数2、目标函数1与约束条件之间的冲突关系。尽管ENV模型支持冲突正反两个方面的表达，但是对于目标函数与约束条件之间的冲突，要以目标函数作为改善参数来定义。这是因为优化的目标是改善参数，而随着设计变量的取值向着可行域边界移动，甚至会超越可行域，这时会引起约束条件的恶化。这类问题对应的冲突模型，一个物理冲突关联多个技术冲突而形成的冲突网络。

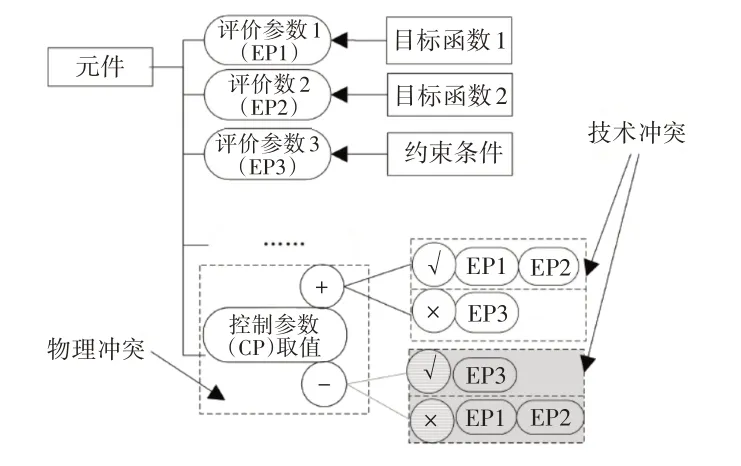
图1 一维优化设计问题中的冲突表达方法Fig.1 Conflict Representation of One Dimensional Optimal Design Problem

2.2.2 多维优化设计问题的转化

多维优化问题包含多个优化设计变量，这类问题在定义冲突的时候，不仅仅需要考虑目标函数之间、目标函数与约束条件之间的冲突，同时也需要考虑各个设计变量之间的取值冲突。约束条件中含有设计变量之间的取值约束关系，这种约束关系在设计变量取值变化时（优化计算过程中），构成了冲突关系。因此这类问题较一维优化设计问题复杂，所转化出来的冲突模型是由多个物理冲突、技术冲突以及二者之间的因果关系构成的复杂的冲突网络。多维优化设计问题中的冲突表达方法，如图1、图2所示。

图2 多维优化设计问题中的冲突表达方法Fig.2 Conflict Representation of Multidimensional Optimization Design Problem

2.3 优化设计冲突的求解方法

从优化设计数学问题提取出来的冲突的求解情况要比在概念设计阶段直接定义的冲突要具体而且复杂。这是因为有如下两种情况：（1）多目标函数、约束条件之间的冲突多构成复杂的多冲突并存的冲突网络。（2）非所有目标函数都能成功地抽象表达为39个工程参数之一，例如：对轨迹综合的优化设计问题中，目标函数要定义为轨迹与目标点的误差。这类问题无法使用39个工程参数表达成为技术冲突，因此TRIZ矛盾矩阵无法直接用于求解。综合考虑优化设计冲突问题，这里提出四种求解方法：

方法I：物理冲突的求解方法

优化设计变量向着多个目标函数优化方向取值，其取值又要受到约束条件的限制，呈现出既应该具有某值，又不能具有某值的物理冲突状态。这种情况需要从设计变量、目标函数、约束条件三者的数学关系来分析和寻找可用资源，改善工作原理。

方法II：技术冲突的求解方法

目标函数和约束条件所表达的工程概念若能匹配到39个工程参数中，则可表达为技术冲突，应用冲突矩阵来求解。

方法III：冲突网络的求解方法

冲突网络是多冲突并存的复杂冲突问题的典型表达形式，目前主要的解决方法主要包括多冲突化简和确定核心冲突并求解两类。文献［13-14］论述了应用OTSM—TRIZ的问题流模型来求解多冲突并存复杂冲突网络的方法；文献［15］采用约束理论（TOC）来表达多冲突设计问题，提出面向多冲突问题分析的设计障碍树（DOT）方法，应用DOT分析确定核心问题并求解；文献［16］采用ENV模型表达多冲突关系，并提出了多冲突关系求解方法；此外，文献［17］提出了基于发明原理使用频次统计的多冲突问题求解方法。这里采用ENV模型来表达优化设计冲突问题，形成物理矛盾与技术矛盾共存的复杂多冲突网络，因此采用OTSM-TRIZ的问题流模型来支持优化设计冲突的求解。

方法IV：基于BioTRIZ的求解方法

部分目标函数或者约束条件抽象为39个工程参数的难度较大，但该类问题中设计变量自身的取值冲突明确。此时，若采用物理冲突求解方法遇到困难，可参考文献［18］所提出的方法。该方法结合文献［19-20］所提出的仿生设计冲突矩阵和生物案例库，提出物理冲突求解的仿生设计方法。不同之处在于，文献［19］采用技术冲突的工程参数来匹配“域”之间的冲突，而这里采用直接将目标函数或者约束条件匹配“域”来完成。这是因为，文献［19］所提出的“域”的概念相比于39工程参数更抽象。此外，当应用TRIZ冲突矩阵所得到的原理对于问题的求解启发效果不佳时，也可采用这里提出的方法转向应用BioTRIZ来求解。

3 参数优化设计与TRIZ理论结合应用的设计过程

3.1 优化设计冲突的求解路径

将优化设计与TRIZ 结合应用时，由优化设计冲突产生的TRIZ冲突表达往往呈复杂的冲突关系，很难直接应用TRIZ理论求解。因此，在优化设计冲突分类及特点和优化设计冲突求解方法的基础上，针对优化设计问题分类构建求解路径，如表1所示。表中，符号“⊕”表示方法选择符号，其中，“A⊕B”表示推荐首选为“A”，若“A”无效再选择“B”，若两者方法单独应用无效，则尝试从“A”与“B”组合应用。例如：“方法II⊕方法I”表示首选“方法II”，若无效则尝试“方法I”，若仍无效，则尝试通过“方法II”与“方法I”的因果关系来组合求解。

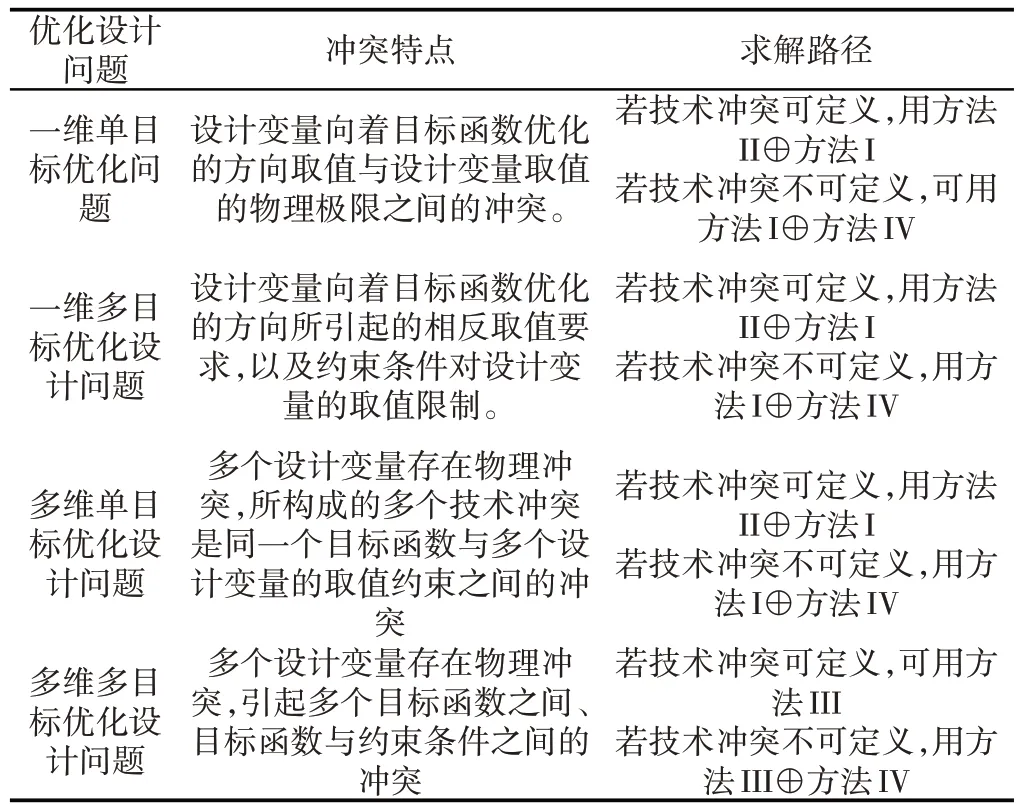
表1 优化设计冲突与求解方法匹配关系Tab.1 Matching Relationship Between Optimal Design Conflicts and Solution Methods

3.2 设计过程模型

将TRIZ理论与参数优化设计结合应用构建其应用流程，如图3所示。具体内容阐述如下：

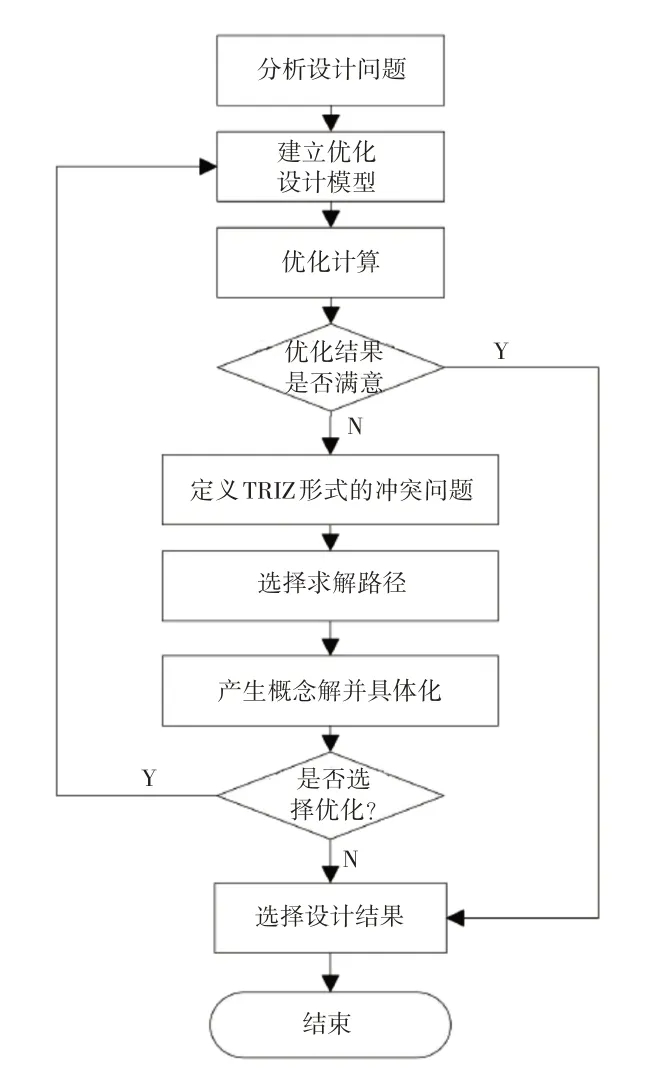
图3 优化设计与TRIZ结合应用设计过程Fig.3 Combined Design Process of Optimization Design and TRIZ Application

（1）分析设计问题

分析目标技术系统的概念解中的设计冲突和设计缺陷的情况。如果存在显示的设计冲突或者设计缺陷，选择概念设计求解方法，例如：TRIZ或可拓学；否则，转入本设计过程，进入下一步。

（2）建立优化设计模型

根据选定的技术目标，分析工作原理，确定设计变量，约束条件以及优化设计目标，建立目标函数。值得注意的是，一些优化设计目标函数构建其显示的解析式难度较大，例如：复杂几何体的体积，这类问题可借助DOE方法和二次回归方程来构建设计变量与设计目标之间的函数关系。

（3）定义TRIZ形式的冲突问题

参数优化设计本质上是采用折中的方式来处理设计目标、设计约束之间的冲突，获得设计变量的取值。因此，从优化设计过程数据中能体现出设计变量的取值所导致的目标函数以及约束条件之间的冲突关系。确定设计冲突后，可采用上文提出的方法，将优化设计的这种冲突关系转化为TRIZ理论中的冲突表达。

（4）选择求解路径

根据优化设计冲突转化为TRIZ冲突的具体情况（技术目标与TRIZ工程参数的匹配情况），以及优化设计的问题类型，如表1所示。选择优化设计求解路径。

（5）产生概念解并具体化

应用选定的求解路径，产生概念可领域化的概念解，确定关键设计变量的值，并做仿真分析，对于满意的设计方案可放入方案集，已备选择。

（6）选择设计结果

这一过程是从方案备选集中选择设计方案的过程。经过参数优化设计和TRIZ理论的应用，方案备选集中包含了前一原理结构的参数优化设计的设计方案和TRIZ理论应用后的具体设计方案两类，选择时需要综合参考技术目标与制造成本等多方面的要求来选择。

4 应用实例

驳接爪是点支式玻璃幕墙连接件的重要组成部分。X型驳接爪是四爪型驳接爪的主要类型，爪臂截面可分为梯形、圆形、正方形、竖矩形和横矩形。点支撑玻璃幕墙受力主要来自于重力和玻璃平面上的风载压力。选X型驳接爪，其臂部截面形状为竖矩形结构，如图4所示。目前驳接爪的主要存在的问题是结构不合理、造材料浪费。

图4 X型竖矩形截面驳接爪结构图Fig.4 Structure of the X-Shaped Vertical Rectangular Section Barging Jaw

这里以316不锈钢某型号竖截面驳接爪为设计对象，考虑材料用量、刚度、强度以及疲劳寿命四个因素，进行结构设计。选驳接爪整体宽度250mm，平面风压载荷2500N，重力1500N。根据驳接臂与驳接头的接口处强度和刚度要求，选择驳接臂截面的宽度为设计变量，并根据驳接头位置的联结端高度，限定设计变量的取值范围为（7～11）mm，驳接臂采用材料316不锈钢，其属性，如表2所示。

表2 316不锈钢材料属性Tab.2 Stainless Steel 316 Material Properties

为验证本文提出的方法，采用Ansys Workbench软件进行仿真和优化设计，具体内容如下：

在设计变量初值（驳接臂竖矩形截面的臂宽）取9.1mm，计算给定载荷条件下的等效应力，变形并绘制疲劳敏感曲线，如图5所示。

图5 优化前驳接爪仿真结果Fig.5 Simulation Results of the Barge Jaw Before Optimisation

为减小材料消耗，以驳接爪的体积作为优化设计的目标，以强度和变形为约束条件，综合考虑疲劳寿命，对驳接爪进行参数优化设计。仿真结果，如图6所示。

优化计算结果数据，如表3所示。其中，图6（a）为等效应力，图6（b）为变形，图6（c）为疲劳敏感曲线，如图6所示。

表3 初始设计与优化设计结果对比Tab.3 Comparison of Initial and Optimised Design Result

将优化设计与原设计比较可知：驳接臂体积减小了11.003%；优化设计前最大应力位置在转接头的上表面，优化设计后最大应力位置在驳接臂的上表面，最大应力值有明显降低，虽然变形有一定增加，但在刚度条件允许范围之内；疲劳寿命不受风载荷影响的载荷倍数由0.7倍变为1倍。

并对比原始设计与优化设计，发现设计冲突。应用ENV模型表达冲突，并选择求解路径进行求解，具体如下：

分析优化设计的设计目标、约束条件和设计变量之间的关系可知：该优化设计问题属于一维单目标优化设计问题，设计目标是减少材料，保证刚度和强度在许用范围内。此外，驳接爪工作时处于静止状态，且其体积与材料用量成正比。根据优化计算数据发现在原设计结构中，材料用量越多，应力和变形就越小。因此，定义四个技术矛盾，按照<改善参数，恶化参数>的格式表述：<静止物体的体积，刚度>；<静止物体的重量，刚度>；<静止物体的体积，强度>；<静止物体的重量，刚度>。考虑到设计变量是上述设计目标和约束条件的影响因素，分析提炼物理矛盾：驳接臂的宽度的取值上出现了既要大又要小的需求。因此，基于ENV模型的设计冲突表达，如图7所示。冲突列表，如表4所示。

表4 设计冲突表Tab.4 Design Conflict Table

图7 驳接爪设计冲突模型Fig.7 Conflict Model for Barge Jaw Design

使用TRIZ求解，选择原理解2（抽取），14（曲面化），将产生负面效应的因素（消耗材料而不承担应力的部分）抽出，将臂顶部曲面化，新结构，如图8所示。

图8 X型竖矩形驳接爪新结构Fig.8 New Structure of the X-Shaped Vertical Rectangular Barging Jaw

对于图8所示结构的仿真，如图9所示。将原设计，参数优化设计和应用TRIZ理论产生的设计方案列，如表5所示。

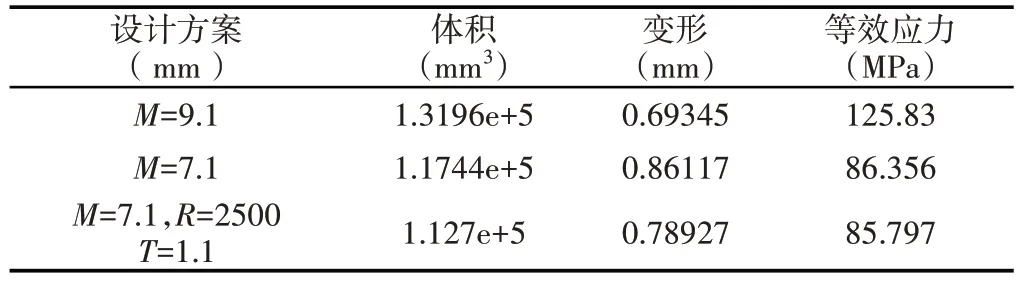
表5 三种设计方案数据列表Tab.5 Data List for the Three Design Solutions

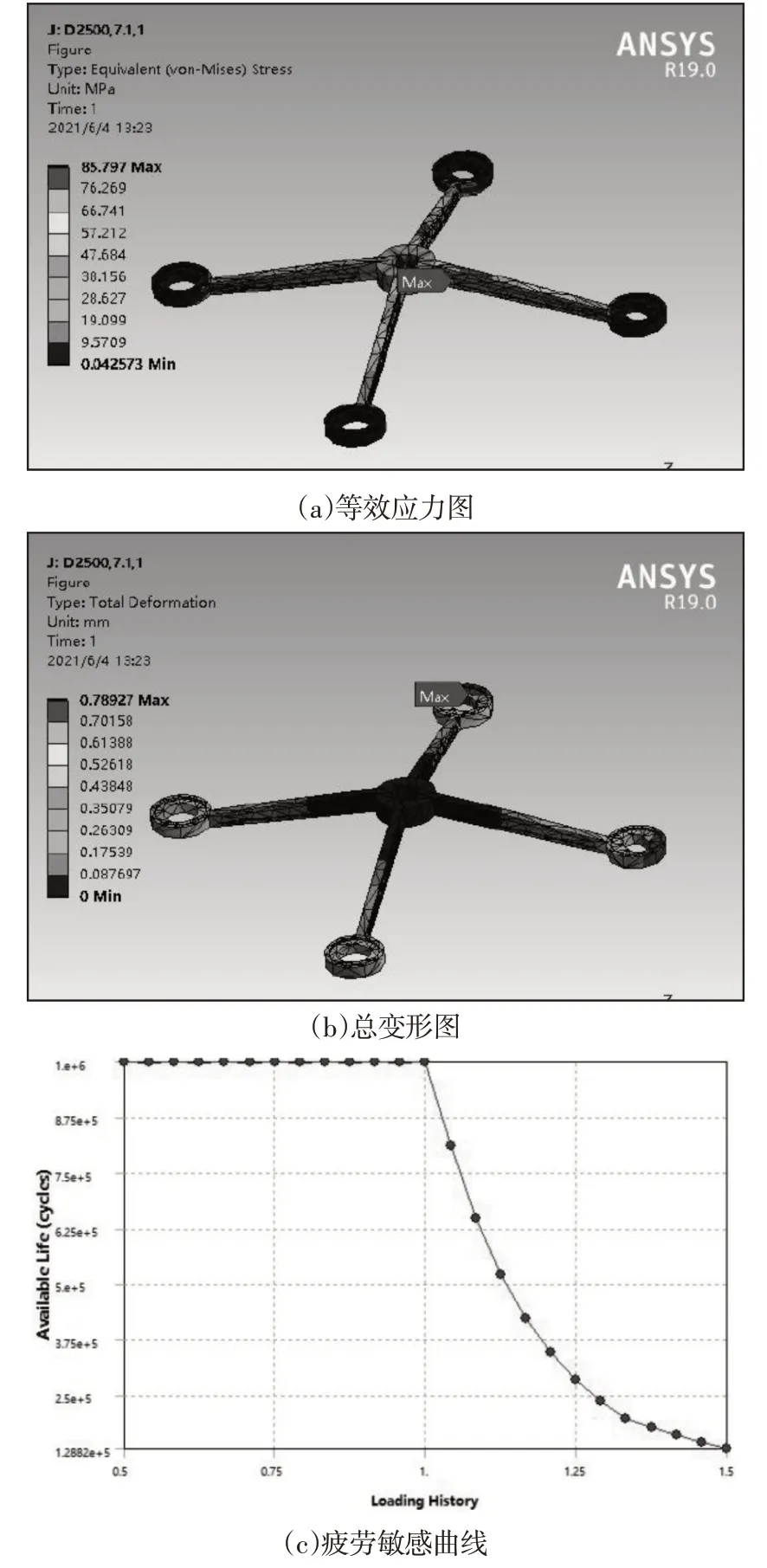
图9 应用TRIZ求解后驳接爪的仿真结果Fig.9 Simulation Results of the Barge Jaw After Applying the TRIZ Solution

表中，设计变量R是驳接臂顶部半圆弧的半径，设计变量T是驳接臂侧面开槽的槽深度。比较三个设计方案，发现在强度、刚度和疲劳寿命三个方面都满足要求，但应用TRIZ获得的解引入了新结构参数，且对比参数优化设计结果，在应力，变形和疲劳寿命三个方面具有改善。此外，体积数据显示：应用TRIZ理论获得的方案与参数优化设计结果相比减小了4.036%；与原设计数据相比减小了14.59%。

根据所提出的设计流程，应用TRIZ产生的方案可进一步以X=[M，R，T]T作为优化设计的设计变量进行参数优化设计，进入设计迭代。

5 结论

将参数优化设计与TRIZ理论结合，构建概念设计与技术设计的迭代设计过程。这一方法产生的解集，综合了参数优化设计对设计冲突折中与TRIZ理论通过消除设计冲突来改进概念解两个方面的优势。所形成的解空间，扩展了以任何单一的方式形成的解空间，为新产品开发过程中可行设计方案的选择，提供了更丰富的备选集。