轨道车辆控制系统车下电气箱控制方法研究

王洪波,刘 超,杜 新,黄志坚,章 斌,孙 辉

(1.中车青岛四方机车车辆股份有限公司,山东 青岛 266000;2.常州今创电工有限公司,江苏 常州 213102)

0 引言

轨道车辆控制系统的稳定是保证轨道交通运行安全的关键环节[1]。其中,轨道车辆控制系统车下电气箱是车辆运行中信号控制的关键设备[2]。该设备通过电气的集成,实现车辆的信号传输、控制、制动等。电气箱为轨道车辆提供制动、照明以及信号等重要指令,保证轨道车辆的正常运行。但是由于实际工况复杂,采集的信号波动大,轨道车辆控制系统车下电气箱的控制难度在不断增加[3]。如何提升轨道车辆控制系统对车下电气箱的控制有效性,成为该领域研究的重点问题。

现如今轨道交通的完善程度越来越高,其对车辆中电气箱的要求越来越严格。不但要求其材质轻量化,还要求有强大的控制功能以及有效的控制程度。该设备不但能够正常供电,其中还要包括多种系统的控制,如制动系统、照明系统、牵引系统、信号系统等[4]。要对轨道交通运行车辆中的系统进行集中管控,保证车辆在任何复杂的情况下都能够安全稳定地运行。正因如此,电气箱的控制中一般采用多种组件或车辆控制器进行统一的信号控制,根据信号的一系列跟踪操作保证车辆的有效操控[5]。电气箱的核心是一种芯片,根据芯片实现逻辑信号的检测、跟踪以及控制。因此,轨道车辆控制系统车下电气箱的有效控制主要是通过多种信号的监测实现[6]。目前,电气箱可以实现较多电气器件、系统控制以及信号控制的功能,降低了因体积过大、电气系统控制导致的车辆行驶安全问题。但由于其控制系统的多元化以及信号量的不断变化,导致电气箱的控制出现了一定问题。

为了提升轨道车辆控制系统车下电气箱控制的有效性,本文设计了一种新的轨道车辆控制系统车下电气箱控制方法研究,通过程序算法写入控制箱的芯片,实现逻辑信号的检测、跟踪和控制,以期为轨道交通的安全运行提供一定理论基础。

1 轨道车辆控制系统车下电气柜控制参数提取研究

轨道车辆控制系统车下电气箱控制实际上是对轨道车辆运行中的各个控制系统的管控。因此在车下电气箱控制方法研究中,通过提取关键轨道车辆控制系统的相关参数作为此次电气箱控制的基础数据,实现有效的控制研究。

1.1 轨道车辆电机运行参数提取

在轨道车辆控制系统中,电机运行参数十分关键,但是提取难度非常大。在实际状态中,由于工况复杂,影响参数提取的噪声较多,进而增加了参数的提取难度。电机运行参数能够反映出轨道车辆行驶的速度以及相关的稳定性。为此,通过分析轨道车辆电机特性提取关键电机运行参数。

电机是轨道车辆行驶的动力,也是控制车辆运行速度的关键[7]。因此,在设计控制方法之前,首先分析轨道车辆控制系统中的电机特性。轨道车辆中的电机一般为直线感应电机,该类型电机属于一种特殊的旋转异步电机,在结构上与一般的旋转异步电机较为相似[8],该电机内部结构如图1 所示。

图1 轨道车辆内部电机结构示意图

直线感应电机中具有较多的磁路,在不同等级的转子状态下呈现的状态不一致。在初级次级长度固定的情况下,初级影响次级导致其出现不平衡的状态,若在不固定的状态下又出现较多的组成模式[9]。轨道车辆的电机运行中磁场不连续时要考虑磁场的畸变,这种畸变是一种末端效应,这种末端效应中第四类末端效应是对电机控制影响最关键的。当电机初级与次级相互运作时,次级前行,其前端和初级未工作部分产生一定作用,等次级末端远离初级工作单元时,在楞次效用影响下,电流方向发生了一定变化,此时产生的磁场也影响了次级的正常运行,该部分涡流使整个磁场发生畸变[10],如图2 所示。

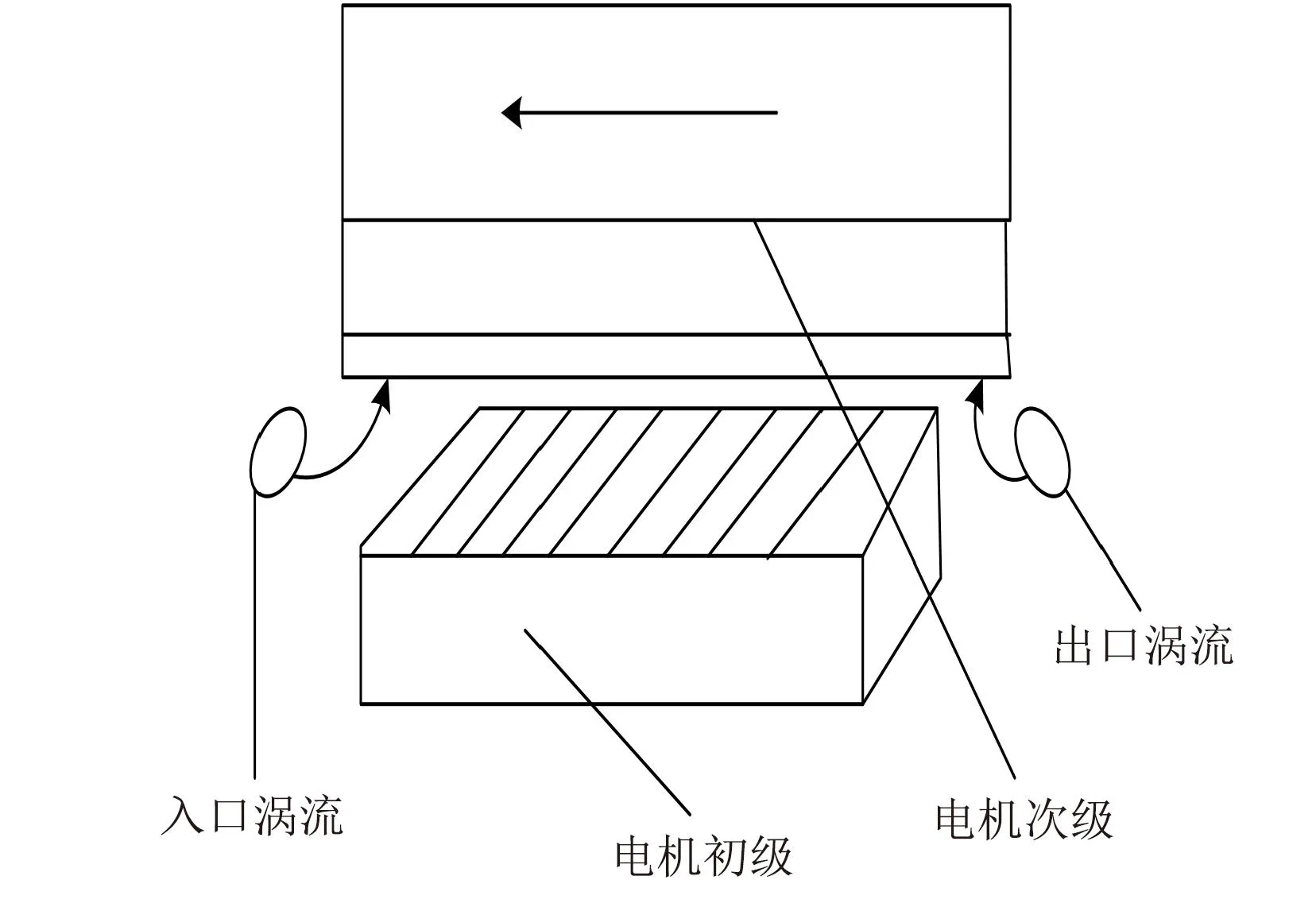
图2 第四类末端效应影响示意图

根据分析的轨道车辆电机特性,为了实现后续的有效控制,保证电机控制时不受到影响,在电机运行参数提取中引入无量纲参数[11]获取轨道车辆直线感应电机信号,得到的结果为：

(1)

式中：Sa为电机初级的长度值,ri为电机的次级电阻,Di为次级电感值,vi为电机运行时的相对速度变化值,e为无量纲参数,f(p)为提取的电机运行信号结果,p为电机的初级电功率。

在轨道车辆电机参数运行提取中,通过分析轨道车辆电机内部基本结构,确定车辆运行时电机运作特性,引入无量纲参数提取有效电机运行参数,为后续的研究奠定基础。

1.2 车辆电气箱热分析

SFE66项目车下电气箱(以下简称“电气箱”)设计采用了封闭机箱结构,仅2处局部开孔并填充过滤棉隔离,相较简易开孔机箱具有更高的IP等级与电磁防护等级。但是,封闭环境散热条件差,如何确保良好的散热性能是该类机箱设计的重点和难点。为此,本计算报告通过仿真分析手段,定义极端的外部环境,考虑不同运行状态下环境、箱体及电气元件之间的热交换对轨道车辆控制效果的影响,通过分析车辆电气箱热情况进行轨道车辆控制模拟分析,以验证该电气箱设计的可行性。

轨道车辆的控制系统通常包括电气控制、信号处理和数据传输等方面,而车辆电气箱则是其中一个重要的部分。车辆电气箱是安装车辆上用于集中控制和供电的装置。车辆电气箱内产生的热量会对车辆控制系统的正常运行产生影响,温度过高会导致电气设备的故障或性能降低。因此,必须采取适当的措施来保证车辆电气箱内的温度处于可接受的范围内,以确保车辆控制系统的正常工作。

①计算条件及输入参数

电气箱箱体由不同规格型材与板材铝合金制成,表面喷漆。电气箱及内部电气元件总装如图3所示。

图3 电气箱总装图

电气箱放置在车下设备舱内,在车体长度方向2/5处位置,如图4所示。

图4 电气箱布置位置示意图

②电气箱几何模型简化

电气箱几何模型简化工作在ANSYS SCDM软件中完成,箱体框架、蒙皮等铝合金板材采用面模型代替。对特征尺寸低于5 mm的凸台、圆角、管件等几何体进行清理,箱体内电气元件采用简化的几何体代替。箱体外部的接线端口及扎线杆对箱体散热影响较小,此处忽略,电气箱简化模型如图5所示。

图5 电气箱简化模型

③流体域建立

由于电气箱内部为封闭的腔体,因此流体计算域分为2个部分,即腔体内部的内流域和外部的外流域。外部流域长度为柜体沿车身方向特征长度的4倍,高度和宽度为柜体特征长度的1.25倍。流体域模型如图6所示。

图6 流体域模型

④网格模型

采用Icepak中Mesher-HD方法划分网格,外流域网格尺寸约为40 mm,内流域及电气元件网格尺寸约为10 mm。模型共有140万个单元。图7～图9为网格模型。

图7 切面网格

图8 电气元件表面网格

图9 箱体面网格

1.3 轨道车辆控制器分析

目前,轨道车辆控制系统主要是通过调整左右车轮的转速对独立轮对进行控制,引导独立轮对能够沿着轨道前进,使轮对在发生偏移时能够及时回正,提高车辆的运行安全性并且降低轮轨磨耗。通过转速差进行反馈控制的最大好处是左右车轮转速差获取成本低,大多轨道车辆都附带有转速测量装置,因此该类方法实用价值较好。

根据反馈量选取的左右车轮转速差,使用比例控制的方法,其输入力矩的计算如式(2)所示。

Tv=hz·βw

(2)

该类控制策略的控制目标是使独立轮对获得类似刚性轮对的导向能力,式中：Tv为输入力矩,hz为基轴制,βw为车轮理想转速差,即βw=0,将其带入到车轮相应的状态方程中可以得到此时轮对的横移状态：

(3)

式中：yw为此时的横移状态,r0为车轮半径,b为横移的距离,λ为车轮荷载,R为车轮的转数,此时,轮对未完全回正(yw≠0),横向位移达到刚性轮对通过曲线时的纯滚线位置。对于刚性轮对,其最小曲线通过半径较大(300 m左右),因此,在该位置上刚性轮对轮缘不会与轨道接触,但是对于独立轮对,车辆通过曲线半径较小(小于100 m),这种情况下,即使轮对中心线位于纯滚线的位置,轮对横移量也会超过阈值。因此,独立轮对其行驶环境的要求使得轮对中心回正到线路中心线的位置,这时,单凭转速差作为反馈量无法满足控制需求,需要补充其他车辆状态信息。

以yw=0为控制目标,当轮对在过曲线达到稳定状态时(忽略轨道不平顺激励以及惯性力),则可以得到该状态下的左、右车轮理想转速差,记为：

(4)

式中：βw为车轮理想转速差;b为横移的距离;V为车轮转速;r0为车轮半径;R为车轮转数。

此外,考虑到控制增益的问题,由于车辆系统状态不断变化,因此,设置固定的控制增益值是符合实际情况的。控制增益的选择需要保证车辆运行范围内控制系统的稳定,可以通过选择较大的一系悬挂纵向刚度,令控制增益与速度的平方呈反比。如下所示：

(5)

综上完成对轨道车辆控制器分析。

2 轨道车辆控制系统车下电气箱控制算法设计

在上述获取的电气箱控制系统的关键参数基础上,为了实现轨道车辆控制系统车下电气箱控制,本文设计了一种新的控制算法。在确定上述的相关参数后,首先通过EKF算法进一步精确辨识提取参数的有效性。该算法是一种基于模型的状态观测器,主要根据轨道车辆电气箱中控制系统的参数继续进行研究,以实现控制参数的离线自整定[12-15]。

假设一个轨道车辆电气箱中控制系统的变量输出和输入存在线性关系,表示为：

w(k)=a1q(k-1)+…anq(k-n)+b0x(k)+

b1x(k-1)+…bnx(k-n)+zk

(6)

式中：w(k)和q(k)分别为输出和输入的参数序列,zk为参数中的干扰因子,a/b分别为不同待辨识的参数。假如从电气箱控制系统中得到k=n+1次的输入参数的观测值,得到的输出控制参数的线性关系为：

x(i)=a1nq(i)+…anq(i)+bnq(i)+di,

i=n+1,n+2…n+N

(7)

式中：x(i)为输出控制参数的线性关系描述,i为输出的控制参数。

为了精准确定控制参数,引入回归系数对参数进行归一化处理,得到的结果为：

L=φϑ+w(k)

(8)

式中：L为控制参数归一化后的结果,φ为回归系数,ϑ为待估控制参数。

在确定电气箱相关系统参数的线性关系之后,为了使后续的控制更为有效,还需要将上述参数进行聚类分析。由于轨道车辆控制系统车下电气箱相关参数对象不是单一的,导致控制参数的数量无法稳定。因此,本文需要引入聚类算法将最相似的参数和距离最近的对象归为一类,根据不同数据之间的距离和相似程度进行整合,将每组参数进行分割,使参数间的距离逐渐变小,直至剩下单独的参数为止。电气箱控制系统的参数聚类分层过程如图10 所示。

图10 电气箱系统参数聚类分层过程

在上述分层过程中,要确定系统参数之间的相似程度和距离,这一过程直接影响参数聚类结果,保证处理后的结果具有一致性。

由于不同参数中所含的主成分不相同,因此,为了保证电气箱控制的稳定性,在实现所有数据控制之前还需要进行约束条件的设置。

在上述确定的电气箱控制参数后,根据参数状态设置轨道车辆控制系统车下电气箱控制参数状态矩阵,得到：

(9)

式中：C为电气箱控制参数状态矩阵,n为控制参数的长度。

当控制参数状态发生一定变化影响到轨道车辆的运行时,此时通过控制电气箱电气系统相关参数实现控制,构建的控制模型为：

(10)

式中：ηi(x)为控制模型描述,λ为电气箱系统变化的特征系数。

3 试验分析

3.1 试验参数设计

为了验证所设计方法的控制有效性,进行了试验分析,试验中轨道车辆的主要参数如表1 所示。

表1 轨道车辆关键参数

具体试验对象如图11 所示。

图11 样本轨道车辆

试验分析中,以该轨道车辆的车下电气箱为研究对象,该电气箱中控制系统参数变化可控,且以本文提取的关键参数为试验的关键数据对象。试验之前提取该试验车辆3个月以来运行的相关数据,该数据通过试验验证。其中,车下电气箱控制系统的参数中存在1 000条异常状态参数,这些参数影响车辆的稳定运行。主要通过分析轨道车辆电机运行参数、运行牵引力参数以及驱动系统控制参数的精度和轨道运行的稳定性。

3.2 试验结果分析

试验首先分析了采用所提方法提取轨道车辆电机运行参数、运行牵引力参数以及驱动系统控制参数的精度结果,为了突出本文方法的可行性,试验中以理想的提取参数精度结果为对比,分析所提方法对控制参数的提取精度,得到的结果如图12所示。

图12 车下电气箱控制参数提取精度结果

从图12可以看出,采用该方法对样本轨道车辆电机运行参数、运行牵引力参数以及驱动系统控制参数的精度较好。将该方法的提取精度和理想精度结果进行了对比,采用该方法提取的每种控制参数的精度较高,最高值可达90%以上,高出了理想值,其可行性得到验证。

试验中,还分析了车辆运行的稳定性,测试的轨道车辆行驶里程为20 000 km,车辆横摆角速度响应结果如图13所示。

图13 轨道车辆运行稳定性结果

从图13的分析结果可以看出,在不对车下电气箱进行控制时,车辆运行的稳定性与参考值差距较大,车辆的横摆角速度变化较参考值较远,且响应的时间也与参考值不同。采用本文方法进行控制后,得到的车辆横摆角速度变化和响应时间均与参考值较为接近。

4 结束语

为了提升轨道车辆控制的稳定性,本文提出研究轨道车辆控制系统车下电气箱控制方法。通过分析轨道车辆控制系统车下电气箱组成系统,确定系统控制参数,根据参数的变化构建控制模型,完成了对该方法的研究。试验结果验证了该控制方法可保证轨道车辆安全运行。