温差热电转换型空间热管冷却反应堆瞬态分析程序开发及验证

葛攀和,李 敏,李杨柳,胡 古,柯国土

(中国原子能科学研究院 核工程设计研究所,北京 102413)

热管冷却反应堆(简称热管堆)是一种新型的反应堆堆型,采用高温热管传热、固态堆芯结构设计,具有结构简单、非能动、高可靠性等优点,在深空探测、星表基地等空间探索任务中具有良好的应用前景。针对空间热管堆电源研究,国外尤其是美国从20世纪90年代开始,开展了一系列热管堆电源设计和研究,较有代表性的是HP-STMC[1]、SAFE-400[2]、Kilopower[3]等典型的空间热管堆电源。在热管堆研发的众多堆型中,最具代表性的是KRUSTY反应堆[4],该堆于2018年完成了带核试验,并开展了一系列稳态和瞬态试验[5],试验结果充分表明了热管堆技术的可行性,也为各型热管堆的研发设计提供了很好的借鉴和参考。

KRUSTY反应堆的温差热电转换为空间电源常用的静态热电转换方式,其热电转换结构简单、技术较为成熟,具有长寿命、高可靠性的特点,因而温差热电转换型热管堆堆电源非常适宜长寿命高可靠的空间探索任务。以电功率为1 kW、采用温差热电转换的Kilopower电源设计方案为例[3],该设计主要由堆本体、屏蔽体、高温热管、温差热电转换器件以及辐射器等部件构成。堆芯热量通过高温热管蒸发段导出,将热量传递至布置在热管冷凝段的温差热电转换模块进行发电,废热通过连接在温差热电转换模块冷端的铝辐射器翅片排放至空间环境中,电源整体设计无运动部件,充分体现了非能动的设计特点。

作为新型反应堆电源系统,其在正常运行以及事故工况下的瞬态特性是电源设计和安全分析中的重要一环。对于热管堆电源系统,国内外也针对不同的电源设计相继开发了相关的系统瞬态分析程序,如PKHPID[6]、FRINK[7]、TAPIRS[8]、HEART[9]等。其中PKHPID用于SAFE-300反应堆传热分析,FRINK程序主要用于Kilopwer以及KRUSTY反应堆的瞬态分析,TAPIRS用于碱金属热电转换系统空间堆电源系统分析,HEART用于海洋静默式热管反应堆的稳态和瞬态分析。由于PKHPID程序堆芯模型仅模拟单个燃料元件到单根热管的传热,无法模拟堆芯径向传热,无法满足如热管失效、热阱丧失等事故工况的分析需求。TAPIRS用于分析碱金属热电转换系统,堆芯燃料元件与热管的传热采用简化模型,燃料与热管之间异形三角区域将其等效为包壳外部的假想层,采用集总参数方法进行堆芯计算。此外国内Guo等[10]采用基于OpenFOAM的堆芯传热模型,耦合RMC开展了反应堆多物理场耦合分析。综上,目前针对热管堆的瞬态分析模型多针对特定的电源设计,在模型上各有差别,尤其是在堆芯传热、热管瞬态模型、热电转换等方面。热管堆区别于液体冷却反应堆,由于采用固态堆芯结构设计,堆芯传热主要以热传导为主,并涉及接触换热、辐射换热等多种换热方式,采用集总参数的模型对几何的适应性较差,如FRINK堆芯模型等对几何结构的依赖性较高,对堆芯局部热点的捕捉能力较差,此外燃料以及堆芯结构之间的换热方式根据具体的堆芯设计差别较大,采用三维CFD方法开展堆芯传热计算和分析则可有效解决上述问题。

本文以温差热电转换型空间热管堆电源系统为主要研究对象,针对该类型的反应堆电源主要部件,如反应堆堆本体、高温热管、温差热电转换系统,建立详细的数学物理模型,其中堆本体模型基于OpenFOAM开发,包括热管堆的堆本体稳态和瞬态传热模型、点堆动力学模型、反应性反馈模型等,在此基础上开发适用于温差热电转换型的热管堆瞬态分析程序,采用文献及试验数据开展程序模块验证,并结合KRUSTY设计和试验结果开展典型工况分析和验证。

1 模型介绍

1.1 堆本体模型

1) 堆本体功率模型

热管堆堆芯功率包括裂变功率和衰变功率。裂变功率由点堆动力学方程计算:

(1)

i=1,2,…,6

(2)

j=1,2,…,n

(3)

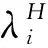
堆芯的裂变功率为:

P(t)=VEfΣfn(t)v

(4)

式中:V为体积;Σf为宏观裂变截面;Ef为单次裂变产生的能量;v为中子速度。

对于上述点堆动力学模型,可通过数值求解算法如龙格-库塔方法[11]进行求解。

2) 反应性反馈模型

热管堆基本采用固态堆芯结构和高温热管传热方式,堆芯反应性反馈主要包括堆芯燃料的膨胀、燃料的多普勒效应、热管材料的温度反应性反馈、热管内工质分布引起的反应性反馈[10]以及堆本体其他部件及结构材料的温度反应性反馈。

反应性反馈模型如下:

ρ(t)=ρ0+ρext(t)+ρd(t)+ρe(t)+ρh(t)+

(5)

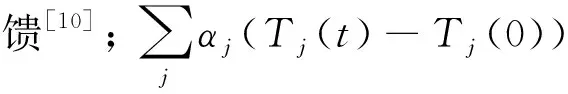
3) 堆本体传热模型

根据目前公开的热管堆电源的堆芯设计方案,典型的堆芯结构如HP-STMC系列和Kilopower系列的设计,前者采用带包壳的燃料元件,燃料元件与热管按照一定的比例进行排布组合,燃料元件与热管之间的异形三角区域通过填充不同的材料构成整个堆芯结构;后者堆芯采用整块铀钼合金燃料作为基体,热管分布式布置在堆芯。两种不同的设计对热管堆堆芯的传热模型带来了不同的要求。如PKHPID程序建立了单个燃料组件到热管的传热模型,对于堆芯甚至堆本体径向方向的传热则无法进行模拟;FRINK程序考虑了块状燃料沿径向方向的传热,对于Kilopower以及KRUSTY的堆芯适用性较好,但程序对于不同堆芯的几何适应性相对较差,尤其是较大功率的复杂堆芯几何结构建模,对于堆芯局部热点的捕捉能力较差。采用三维堆本体传热模型进行堆芯传热可有效解决上述问题,得到较为精确的温度场,本文则以开源计算程序OpenFOAM为基础开发热管堆堆本体传热求解器。

在求解器中,堆芯燃料以及堆本体各部件采用如下导热模型:

(6)

式中:ρ为密度;h为焓值;下标i代表计算域,在热管堆堆本体中则可表示为燃料、包壳、结构材料、反射层等相关部件,其中物性参数采用变物性的温度场求解器。

对于燃料以及各部件内的释热,基于fvOption源项函数进行模块开发。对于燃料以及其他部件内的功率分布,定义了功率分布函数,通过获得计算域内每个计算网格单元cell的坐标位置,根据堆芯功率分布得到该位置处的释热率。

热管堆基本采用固态堆芯的结构设计,堆内各部件之间存在如装配、接触、焊接等结构上的连接关系,不同的部件界面连接关系对堆内温度场的影响差别较大,在堆本体传热模型中需考虑不同部件之间的界面传热模型。在堆本体传热模型中,设置了3种界面传热模型,即两个固体界面无热阻传热、接触传热、辐射传热+间隙导热,如图1所示。界面的传热涉及从属两个不同计算域的网格之间的传热过程。以界面模型1为例,在交界面上考虑界面的法向热流相等,则:

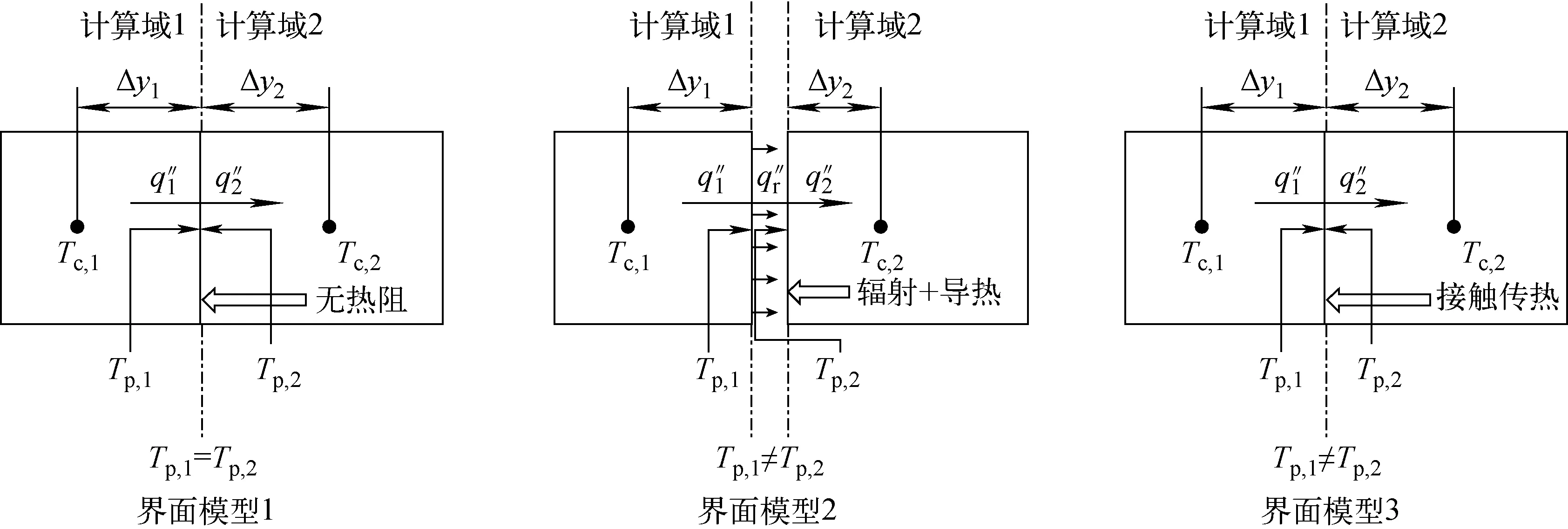
图1 两个不同计算域交接界面上网格示意图Fig.1 Schematic diagram of interface between two computational domains

(7)

(8)

在OpenFOAM中,有3种基础的边界条件,分别为Dirichlet边界(定值边界)、Neumann边界(定梯度)以及混合边界(mixed),其中混合边界表述[12]如下:

Tp=valueFraction*refValue+

(9)

式中:Tp为边界面上网格节点变量值;Tc为边界面对应中心网格变量值。

将式(8)按混合边界形式表示即可实现两个计算域耦合求解。上述界面模型为理想的两个计算域无热阻连接方式,当两部件之间交界面上不直接接触、并假设存在气体介质时,交界面的等效传热系数(hs)为:

(10)

式中:kg为气隙的导热系数;δg为间隙的厚度;σ为斯蒂芬-玻尔兹曼常数;εp,1和εp,2分别为两个接触面的表面发射率。

当两个界面之间接触时,界面之间的传热模型变为接触传热模型,接触热阻的精确模拟较为困难,与接触表面的压力、接触点的变形程度以及材料的热物理性能均相关。本文采用Song和Yovanovichin[13]给出的经验公式求解等效换热系数,即:

(11)

(12)

式中:p为接触压力;Hb为硬度;db为维氏显微硬度关系式系数;σs为接触表面粗糙度均方根;m为平均表面粗糙峰斜率。根据式(11)中的等效换热系数,可得到:

(13)

根据能量守恒有q″1=q″2,基于上述交界面热流的表达式,采用混合边界形式开发了界面传热模块,用于热管堆各部件之间的界面传热。

热管堆堆本体传热求解器基于多域求解器chtMultiRegionFoam开发,在该求解器的基础上增加了点堆动力学方程求解模块、反应性反馈模块、堆芯释热及功率分布模块,并开发了界面传热模型,具备热管堆堆本体稳态和瞬态传热计算能力。

1.2 高温热管模型

高温热管主要由管壁、吸液芯和蒸气区构成,依靠热管内液态金属在吸液芯表面的气液相变实现高效传热。高温热管的自凝固启动过程可分为5个阶段[14],该过程涉及较复杂的物理过程,包括工质的熔化凝固、气液界面的蒸发冷凝、蒸气的不同流动状态(包括自由分子流、过渡流和连续流动)等。本文中高温热管启动过程采用尘气模型模拟,参见文献[15]。对于热管内建立连续流后的模拟,采用本文模型(式(14))进行模拟以提高计算效率。通过克努森数Kn表征热管内蒸气连续流动是否建立,当Kn小于0.01时认为热管内蒸气处于连续流动状态,可通过判断转变温度(Ttr)来判断是否处于连续流阶段。克努森数Kn为分子的平均自由程与蒸气腔直径的比值,只有当Kn小于0.01时分子的平均自由程相比热管蒸气腔的直径可忽略,此时热管内的蒸气可认为处于连续流动状态。

(14)

式中:D为蒸气腔的直径;ps为蒸气饱和蒸气压;kB为玻尔兹曼常数。当蒸气温度T>Ttr时,认为管内蒸气达到连续流阶段。

针对高温热管启动后的瞬态过程模拟,建立了二维热管模型,包括管壳、吸液芯以及蒸气区,管壳模型采用固体导热模型计算,如式(15)所示。

(15)

在吸液芯内,考虑到工质的流速相对蒸气低得多,且液态金属的导热系数很高,因此吸液芯内的传热主要以导热为主,由于工质的流动导致的温差很小,因此忽略工质的流动性[16],采用纯导热模型进行吸液芯区域的传热计算。吸液芯的控制方程可简化为下式:

(16)

ρtothtot=εglρlhl+ε(1-gl)ρshs+(1-ε)ρmhm

(17)

式中:ε为吸液芯丝网的孔隙率;h为工质或吸液芯毛细介质的焓;ρ为工质或吸液芯毛细介质的密度;keff为有效导热系数;下标l、s、m分别代表液态工质、固态工质和吸液芯结构材料;gl为工质液态份额,工质处于固态时为0,处于液态时为1。根据焓值与温度的关系,热管蒸气处于连续流时,工质已处于熔化状态,因此gl为1。将式(17)转化为温度的控制方程,则有:

(18)

对于高温热管吸液芯,同时存在固体和液体材料,采用Chi[16]公式计算吸液芯控制单元的有效热导率:

(19)

式中:km为吸液芯材料的热导率;kl为工质的热导率;keff为吸液芯的有效热导率。

高温热管主要通过吸液芯表面的气液相变进行高效热量传输,涉及工质在气液界面的蒸发和冷凝,根据分子动理论[17]得到气液界面的传质速率来模拟蒸发和冷凝过程:

(20)

式中:a为蒸发冷凝系数;Ru为常数;M为相对分子质量;Tl为气液界面液态工质温度;pl为液态工质的饱和蒸气压;Tg为蒸气腔内蒸气平均温度;pg为蒸气的饱和蒸气压。则单位长度上热管的传热功率为:

hfgΔLiΔWi

(21)

其中:hfg为相变潜热;ΔLi和ΔWi为气液交界面上第i个节点长度和宽度。则通过蒸发段气液界面的传热功率为:

(22)

当热管内蒸气完全处于连续流动状态时,忽略蒸气流动带来的热阻[14],认为蒸气腔中温度均匀分布,则根据气液界面的质量和能量守恒得到:

(23)

式中:me为蒸发段节点数;mc为冷凝段节点数。

根据热管沿轴向气液界面处液相的温度求解式(式(23))即可获得蒸气区的温度,进而获得气液界面的蒸发冷凝率以及不同位置处的界面热流,耦合求解管壳、吸液芯以及蒸气模型即可获得高温热管启动后的瞬态响应特性。

1.3 温差热电转换模型

空间热管堆电源系统根据不同的应用需求以及功率范围会采用不同的热电转换方式,本文重点针对温差热电转换系统进行了建模分析。图2为典型的温差热电转换单元,热量通过上方的覆铜基板依次经过p型和n型热电材料,发电功率通过外部接线连接至负载侧,热电转换后的废热通过冷端的基板进行排放。

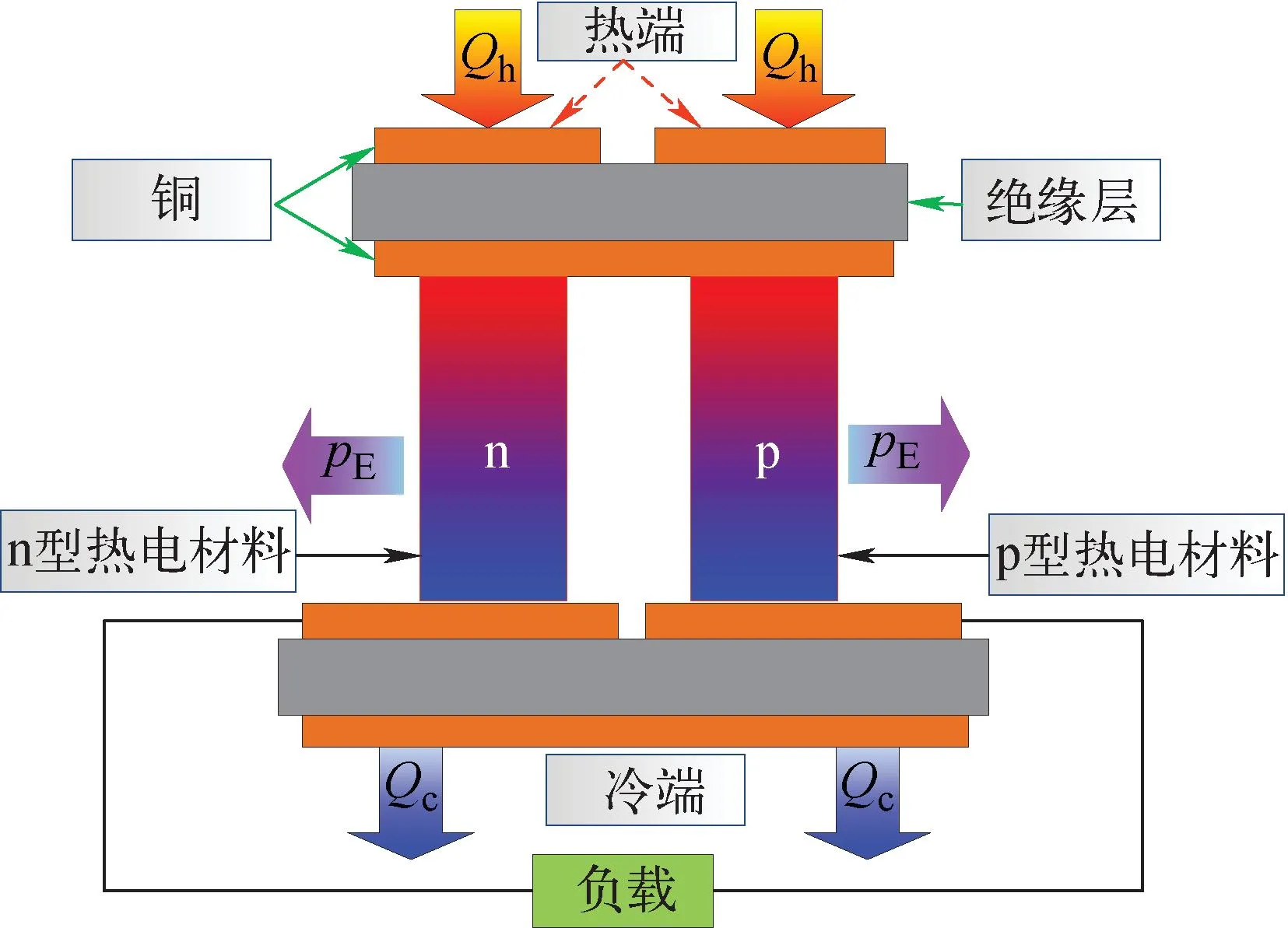
图2 温差热电转换单元结构示意图Fig.2 Schematic diagram of thermoelectric conversion couple

在p型和n型热电材料中,涉及的主要温差电效应为塞贝克效应、珀尔帖效应和汤姆逊效应,当电流流经热电材料后,焦耳热产生于整个负载回路,珀尔帖热则产生于电偶臂和铜电极交接面。绝缘层用于电绝缘,连接电偶臂的铜电极与外部接线共同构成电回路,顶部和底部的铜与热端换热器和冷端集成连接。基于以上热电单元基本结构,本文建立了一维热电单元瞬态模型,在模型中忽略电偶臂侧面的对流或辐射换热,对于模块级的热电单元,其功率输出以及电压分别根据所包含的单元数和串并联关系计算得到。热电转换单元瞬态模型包括p型和n型电偶臂以及端部电极连接的数学模型[18],如下式所示:

(24)

(25)

(26)

式中:ρ为密度;cp为比热容;k为热导率;σ为电导率;β为汤姆逊系数;J为局部电流密度;下标p,n,conn分别代表p型和n型热电材料以及电极连接。式(26)右边第1项代表导热项,第2项和第3项代表由于焦耳热和汤姆逊效应导致的内热源。其中汤姆逊系数可通过塞贝克系数得到:

(27)

式中,α为塞贝克系数。对于绝缘陶瓷基板以及顶端和底部的铜导热片,则采用下式计算:

(28)

发电效率(η)为热电单元的电功率(Pe)与热源输入至热端的热功率(Qin)的比值:

(29)

式中:Th为热端温度;Tc为冷端温度;RL为外部负载的阻值;Rint为发电单元的内阻。

发电单元的开路电压E通过将每个电偶臂网格单元的压降相加得到:

E=α′(Th-Tc)

(30)

(31)

(32)

(33)

(34)

输入至热电单元热端的功率按p型和n型的两段节点进行计算:

(35)

(36)

式中:αpn=αp-αn为热电单元的塞贝克系数;N、M为节点数。

将上述控制方程在空间网格节点上进行一维数值离散即可获得关于时间的控制方程组,通过求解控制方程组即得到温差发电单元温差场,根据式(29)可获得温差发电单元的发电功率、效率等参数。

2 程序开发与验证

2.1 数值算法

将上述热管堆电源系统各部件和系统的数学物理模型转化为热管堆系统热工水力特性的控制方程组,通过求解该方程组即可获得电源在各类瞬态工况下的特性。其中,堆本体模型计算采用OpenFOAM内置的求解器完成稳态和瞬态求解。高温热管、温差转换系统等其他系统部件的控制方程的基本形式为主要热工状态变量对时间的导数以及与本身之间的显式或隐式的函数关系,通过空间离散均可转化为非线性常微分方程组的初值问题,一般具有如下形式:

(37)

通过求解该方程组即可获得各状态参量,本文中上述方程组的求解以开源的SUNDIALS[19]函数库作为基础求解器,程序采用其内部的CVODE或ARKODE两个求解器,可采用显式或隐式的方法进行求解。在底层求解器基础上,基于模块化的编程思想,采用C++语言将电源系统内各部件模型进行封装,系统中每个简单或复杂的部件均采用相应的数据结构进行描述。程序主要由系统数学物理模型模块、材料物性模块、接口管理模块、求解器模块等构成,其中各部件模型之间的数据传递及控制方程组的求解均统一由求解器模块实现。图3为主要求解流程。

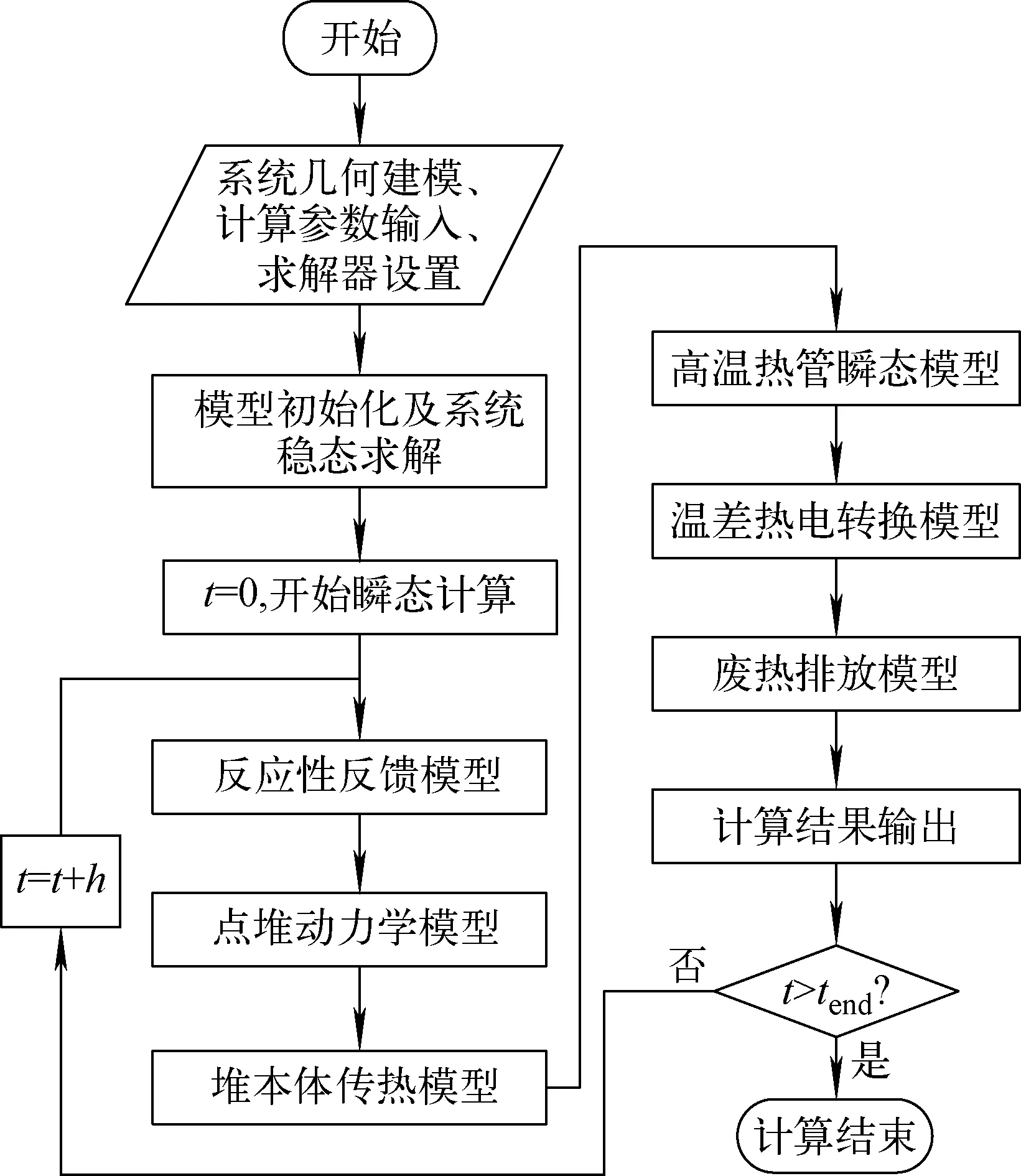
图3 系统瞬态分析程序计算流程图Fig.3 Calculation process of transient analysis program

2.2 程序模型验证

1) 热管程序验证

高温热管启动阶段的模型验证参见文献[15],针对热管启动后管内处于连续流的瞬态过程,分别采用热阻网络模型[20]和1.2节模型开发了热管瞬态分析模块,通过文献[20]给出的参数进行对比验证,计算采用的几何物性参数列于表1。

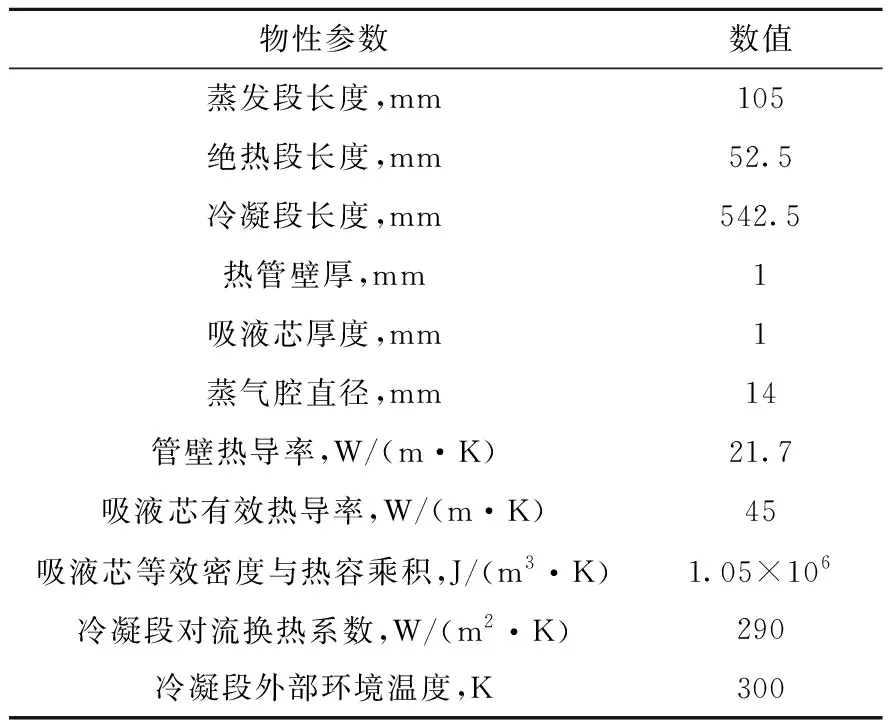
表1 钠热管结构参数Table 1 Parameter of sodium heat pipe

计算中蒸发段壁面设置恒热流边界条件,初始时刻为输入功率623 W,之后将加热功率提升至770 W,图4为由1.2节模型和热阻网络模型计算得到的蒸气温度与文献[20]中计算结果的对比,可看出计算结果符合较好。

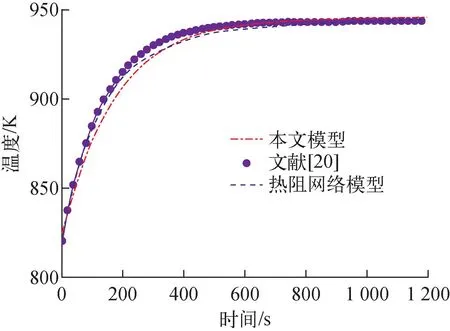
图4 热管升功率瞬态过程中蒸气温度模型计算结果与文献结果的对比Fig.4 Comparison of model calculation and literature results of heat pipe vapor temperature during input power increasing condition

2) 温差热电转换验证

温差热电转换模块的验证根据文献[21]给出的商用BiTe型温差发电器件试验值进行,该器件包含127个p-n热电单元,单个p-n热电转换单元的结构示意图如图5所示,主要由陶瓷基板、铜以及BiTe热电材料构成。p型和n型热电臂的面积Ap=An=1.4 mm×1.4 mm、长度均为1.6 mm,陶瓷基板厚度为1.0 mm,铜电极片厚度为0.4 mm。热电材料与铜片之间的接触热阻和接触电阻分别为5×104W/(m2·K)和5.6×107S/m2[21]。器件测试时,热端采用电加热器控制温度,冷端采用水冷维持温度。试验测试了两组冷热端温度(Th=458 K、Tc=303 K和Th=463 K、Tc=318 K)条件下器件输出功率随负载热阻RL的变化曲线。试验重复3次,测试结果的误差较小,不超过3%[22]。

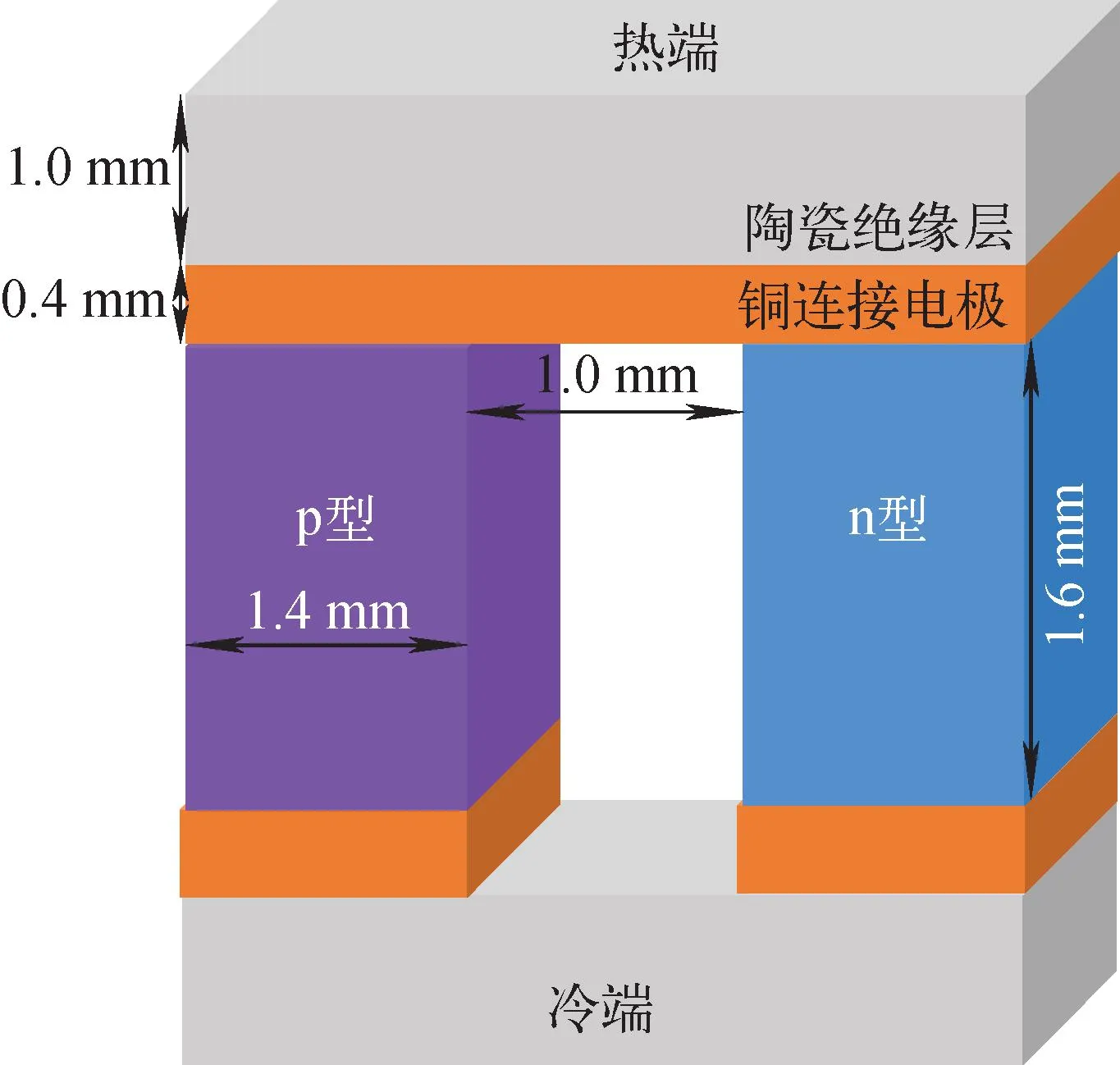
图5 BiTe型温差发电单元结构示意图[21]Fig.5 Schematic diagram of BiTe thermoelectric module[21]

图6为本程序模拟的器件输出电功率与试验结果的对比。由图6可看出:程序计算得到的器件输出电功率与试验数据符合较好,两组冷热端温度条件下器件最大输出功率与试验值的相对偏差分别为2.47%和2.75%;随着外部负载热阻的不断增大,器件输出电功率逐渐增加到最大后又缓慢减小,符合温差发电器件的发电特性。

图6 器件输出电功率与测试结果的对比Fig.6 Comparison between simulation and test results of output power

3 KRUSTY反应堆瞬态分析验证

KRUSTY反应堆是Kilopower反应堆的地面原型测试系统,用于验证Kilopower空间反应堆电源的设计以及动态特性,于2018年5月完成最终核测试。在KRUSTY带核试验期间开展了一系列试验,包括反应堆启动停堆、负荷跟踪、反应性调节、模拟斯特林失效、热阱丧失等瞬态工况,充分验证了反应堆的非能动传热、避免单点失效的特性。本文以KRUSTY反应堆作为瞬态分析程序的分析和验证对象,分别开展负荷跟踪、热电转换模块失效、反应性控制、热阱丧失工况的模拟分析,通过试验结果进行对比验证。

3.1 KRUSTY反应堆描述

KRUSTY反应堆堆芯采用高富集度铀钼合金(U7.5Mo)为燃料,堆芯轴向反射层以及径向侧反射层均采用BeO,通过可上下移动的径向反射层进行反应性控制。堆芯热量通过8根包壳材料为Haynes230的高温钠热管导出,钠热管与燃料之间的热连接通过外部紧箍环施加压力实现。钠热管将反应堆的热量传递至2台斯特林发电机以及6台斯特林模拟器进行热电转换,其中6台模拟器不发电,通过控制输入的氮气流量模拟实际斯特林的热量输出。反应堆堆芯外侧均设置有多层钼绝热层以减小堆芯漏热,堆芯活性区整体位于316不锈钢真空容器中,堆芯结构如图7所示。

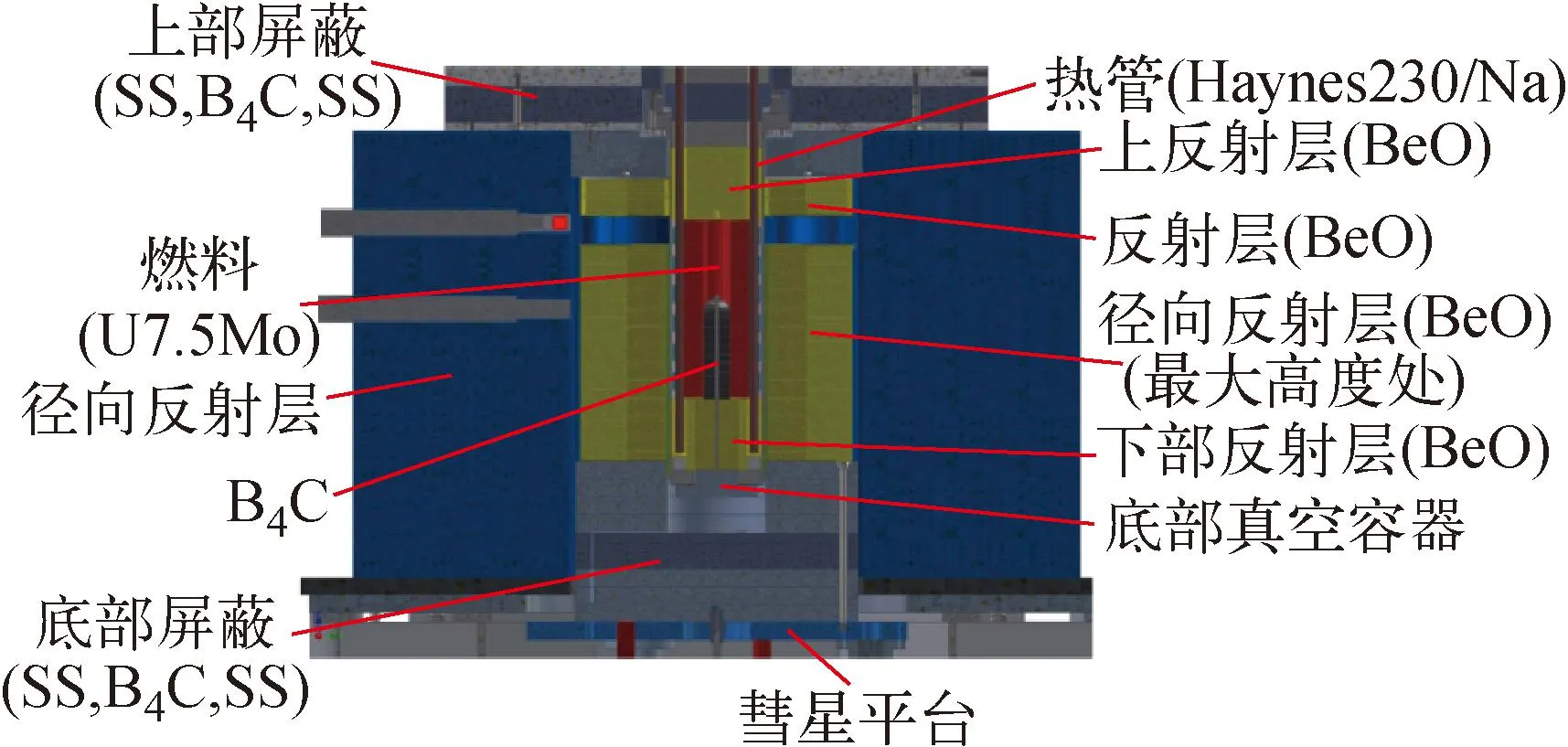
图7 KRUSTY堆芯结构侧视图[23]Fig.7 Side view of RUSTY core[23]

3.2 反应堆建模

根据KRUSTY反应堆的设计,在OpenFOAM中建立反应堆堆芯的传热模型。工作温度下反应堆各主要部件的温度反应性反馈系数(RTC)列于表2。可看出,燃料的温度反应性反馈为反应堆主要的反应性反馈来源,考虑到反应堆活性区侧面均设置隔热层用于防止堆芯漏热,为提高计算效率,堆本体模型只建立活性区燃料、中心B4C以及上下轴向反射层,燃料与上下轴向反射层之间的隔热材料在计算中采用界面间隙热阻方式进行处理。根据反应堆的设计建立8个热管传热模块,斯特林发电机以及模拟器模块根据试验给出的冷却能力,采用设定边界条件的形式进行简化。反应性反馈模块的计算考虑了燃料、上下轴向反射层、高温热管的温度反应性反馈效应,同时考虑了试验过程中由于径向BeO反射层的升温导致的温度漂移,径向反射层的升温速率较小,约为1 ℃/h。上述部件的功率份额以及堆芯活性区的功率分布参见文献[4]。

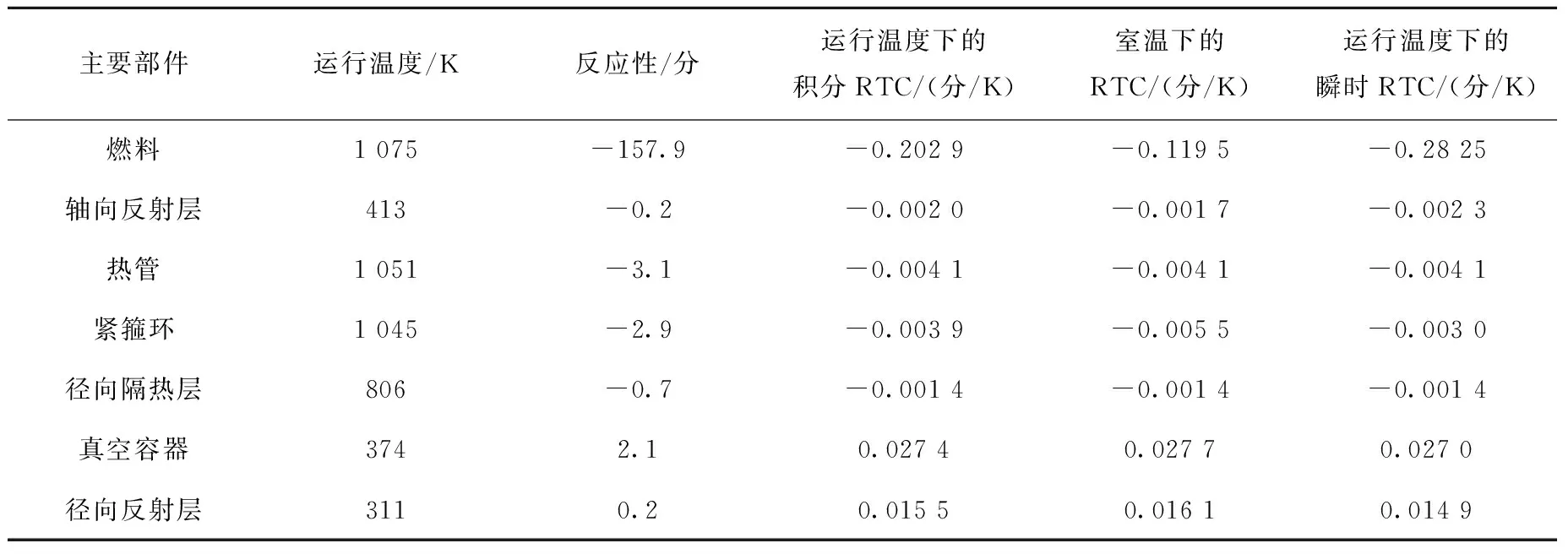
表2 KRUSTY反应性反馈系数[4]Table 2 Reactivity feedback of KRUSTY[4]

3.3 负荷跟踪瞬态工况

为获得Kilopower反应堆系统的负荷跟踪能力,在试验开展的第8～12 h之间开展了负荷跟踪测试。在t=10.02 h时,6台斯特林模拟器的输出功率呈阶跃式提高,通过增加模拟器输入的氮气流量使输出功率接近原来的2倍,由于2台斯特林运行功率已略高于额定功率,因此2台斯特林发电机的输出功率维持不变。模拟器功率的上升导致堆芯功率从2.75 kW增加至4.05 kW,提高了1.3 kW,每台斯特林模拟器的功率也从初始的295 W提高至510 W。图8为负载功率提升工况下堆芯功率和温度随时间的变化。由图8可看出,随着模拟器输出功率的上升,燃料的温度迅速下降,在负温度反应性反馈作用下堆芯功率迅速上升,堆芯功率的上升迟滞了温度下降,导致堆芯功率和温度经历了几次振荡,最终趋于稳定,该过程持续约20 min。图9为堆芯燃料在不同时刻的温度场分布。由于燃料热导率较高,燃料整体温差较小,受功率分布的影响,燃料的最高温度集中在中心区域。在瞬态过程中,程序计算的燃料外侧最低温度与试验值相差4.8 K,达到稳定时与试验值相差1.4 K,可见程序的计算结果与试验值符合较好。

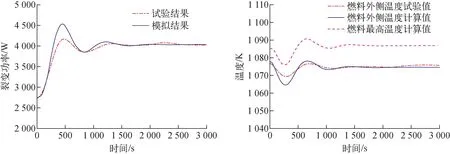
图8 负载功率提升工况下堆芯功率和温度随时间的变化Fig.8 Reactor core power and temperature variation under load power increasing condition

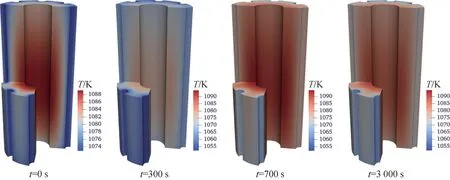
图9 负载功率提升工况下堆芯燃料温度场分布随时间的变化Fig.9 Fuel temperature variation under load power increasing condition

3.4 热电转换模块失效工况

KRUSTY在试验的第12～14 h之间开展了斯特林模块失效测试,验证反应堆避免单点失效能力,测试中通过切断斯特林模拟器的氮气流量来模拟斯特林模块的失效。在t=12.0 h时,切断0°方位角处斯特林模拟器流量,模拟该模块的失效。随着流量被切断,该模块的冷却功率由290 W降低至120 W。在t=12.5 h时,其他模拟器的氮气流量增加到正常功率水平,冷却功率达到约2.85 kW。t=13.0时,切断180°方位角处斯特林模拟器氮气流量,模拟2台斯特林模拟器同时失效的工况。图10为试验值与计算结果的对比,其中温度分别为位于0°和180°方位角附近燃料外侧温度。根据试验结果和计算结果可看出:0°方位角处斯特林模拟器冷却被切断后,对应该角度区域的燃料温度迅速上升,与此同时180°位置处的燃料温度则迅速下降。t=12.5 h时,其他模拟器的氮气流量增加导致输出功率增加,燃料平均温度下降,之后在负温度反应性反馈作用下堆芯功率经历2次振荡过程。当2台斯特林模拟器同时失效时,由于堆芯输出功率减小,导致燃料的平均温度上升,其中失效模拟器位置的燃料温度由于失去冷却迅速上升。图11为不同时刻堆芯燃料温度场的变化,第500 s和4 300 s分别对应1台斯特林模拟器失效以及2台斯特林模拟器同时失效时的燃料温度场,失效斯特林模块由于输出功率减小对应位置处燃料温度明显高于其他模块。对于KRUSTY反应堆,当2台斯特林同时失效时,堆芯仍可正常运行,体现出较好的抗单点失效能力。根据试验测试结果,45°处燃料外侧温度从t=12.0 h至t=13.0 h升高约8 K,程序计算结果为升高9.3 K,相差1.3 K,堆芯功率的最大相对偏差小于3.2%,计算结果与试验结果整体符合较好。

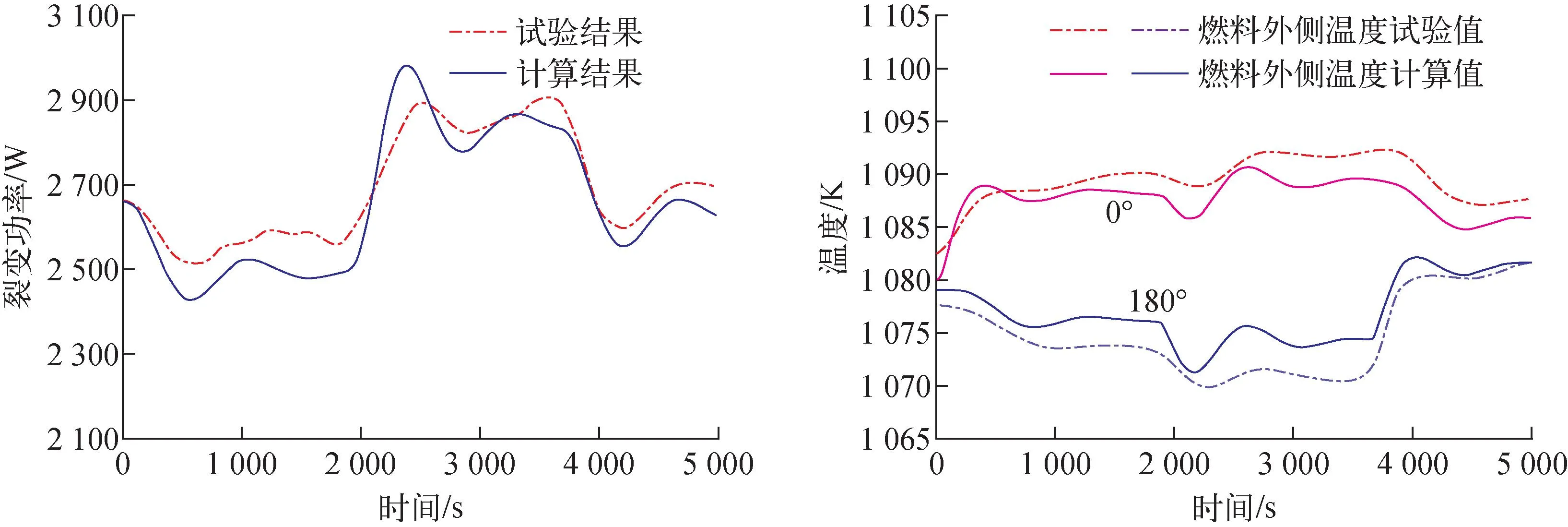
图10 斯特林模块失效工况下堆芯功率和燃料温度随时间的变化Fig.10 Reactor core power and temperature variation under Stirling module fail condition

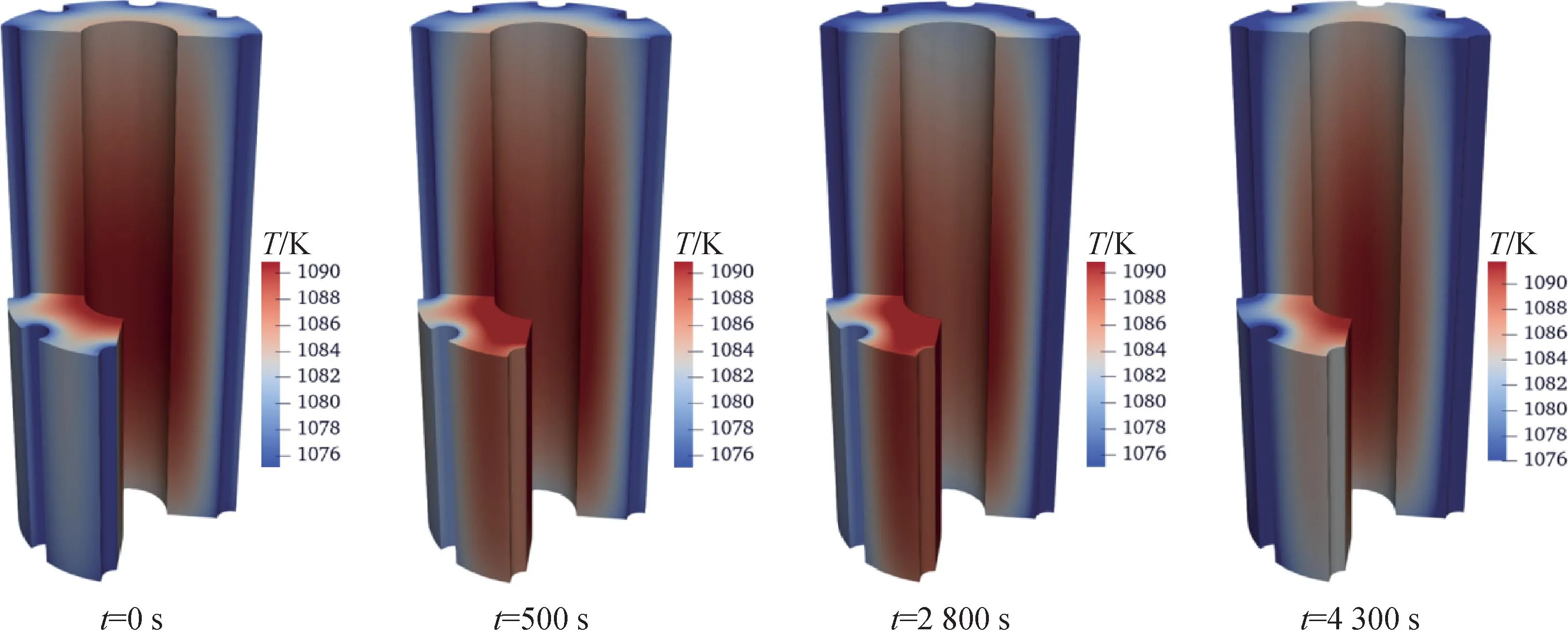
图11 斯特林模块失效工况下堆芯燃料温度场分布随时间的变化Fig.11 Fuel temperature distribution under Stirling module fail condition

3.5 反应性引入瞬态工况

反应性引入瞬态测试用于测试系统反应性变化过程中系统瞬态响应过程,在测试中通过移动径向反射层实现系统反应性的增加或降低。在t=16.00～16.05 h期间,径向反射层逐渐降低了0.5 mm,引入约-5.5分反应性,在此过程中斯特林模拟器功率输出基本保持不变。图12为反应性控制工况下堆芯功率与燃料温度随时间的变化,可看出反应性引入后堆芯功率迅速下降,同时燃料外侧温度及最高温度也开始下降,燃料温度下降引入了正反应性,迟滞了功率的下降,之后堆芯功率又开始回升,在反应性反馈作用下堆芯功率经历几次波动后达到稳态。图13为燃料在不同时刻的温度场,在第600 s时燃料的温度接近最低值,整体温度场分布更加均匀。该瞬态过程中裂变功率最小值约为1.3 kW,程序计算结果为1.436 kW。在该瞬态过程中燃料的温度试验值下降了约29 K,程序计算的燃料温度下降26.1 K,相差2.9 K,计算结果与试验值符合较好。

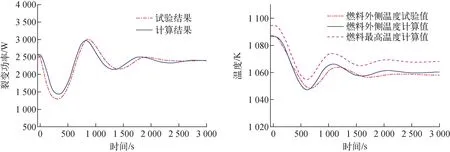
图12 反应性引入工况下堆芯功率和燃料温度随时间的变化Fig.12 Reactor core power and fuel temperature under reactivity control condition

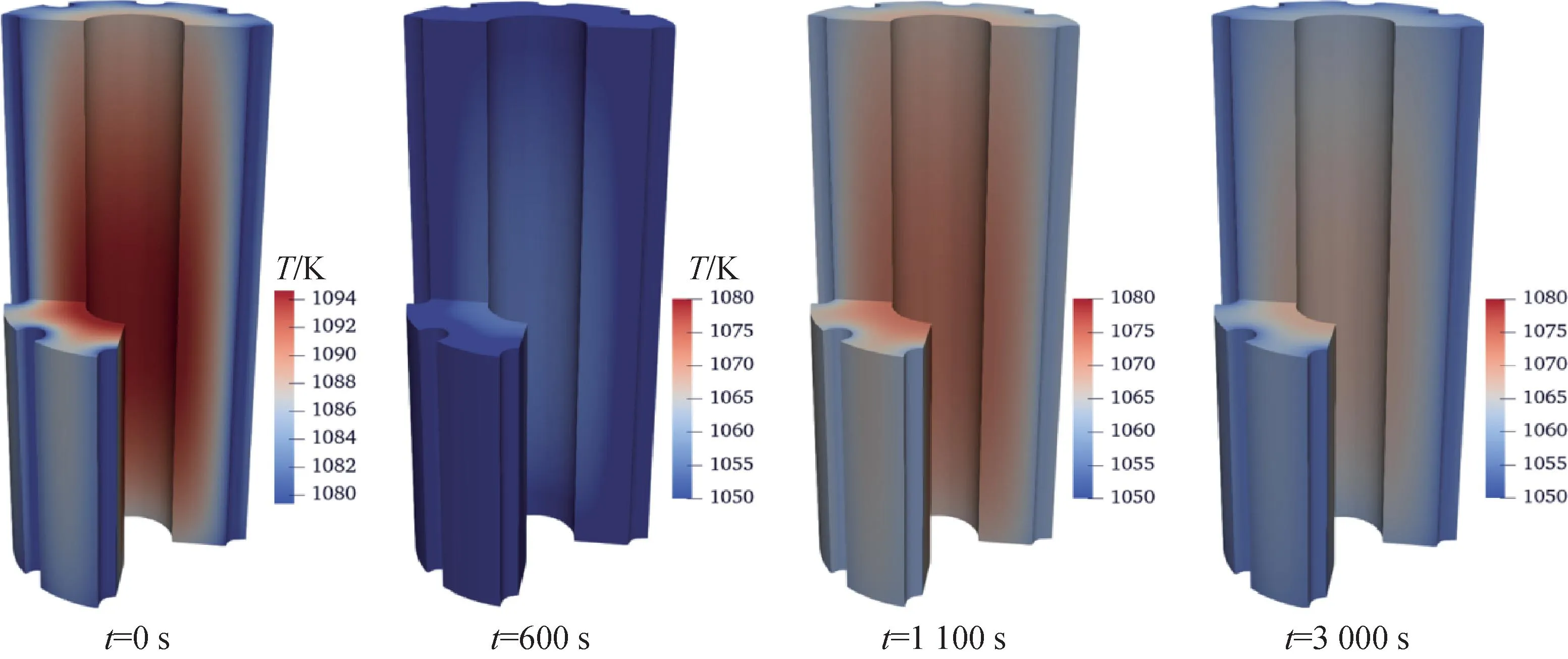
图13 反应性引入工况下堆芯燃料温度场分布随时间的变化Fig.13 Fuel temperature distribution under reactivity control condition

3.6 主动冷却丧失工况

KRUSTY在试验末期开展了主动冷却丧失试验,验证反应堆的安全性和动态特性。在t=20 h时,2台斯特林停机,因斯特林模拟器的流量设置在一个非常低的流率,在该试验条件下,堆芯的稳态功率从2.6 kW降低至1.5 kW,2台斯特林完全停机后仍具有一定的热损失,约为75 W。图14为堆芯功率与燃料温度随时间的变化,当斯特林和模拟器冷却能力基本丧失后,燃料的温度迅速上升,在负温度反应性反馈作用下堆芯的功率也迅速下降,导致堆芯功率从2.6 kW下降至1.25 kW,之后又由于功率降低导致温度开始下降,直至达到新的稳态。图15为不同时刻堆芯燃料的温度场,400 s时燃料的温度最高,5 000 s时堆芯功率基本达到稳态值,由于功率下降了1.35 kW,燃料的温度梯度相比初始时刻更小。本程序计算得到堆芯最低功率为1.068 kW,燃料外侧最高温度试验值约为1 102.6 K,本程序计算值为1 106.7 K,高出试验值4.1 K,计算结果与试验值符合较好。通过该瞬态工况可看出,KRUSTY在堆芯热管完全丧失主动冷却情况下,反应堆在温度负反馈作用下仍可通过被动的散热维持低功率运行。

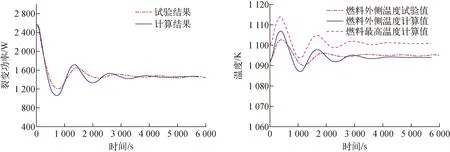
图14 主动冷却丧失工况下堆芯功率和燃料温度随时间的变化Fig.14 Reactor core power and fuel temperature under active heat removal condition

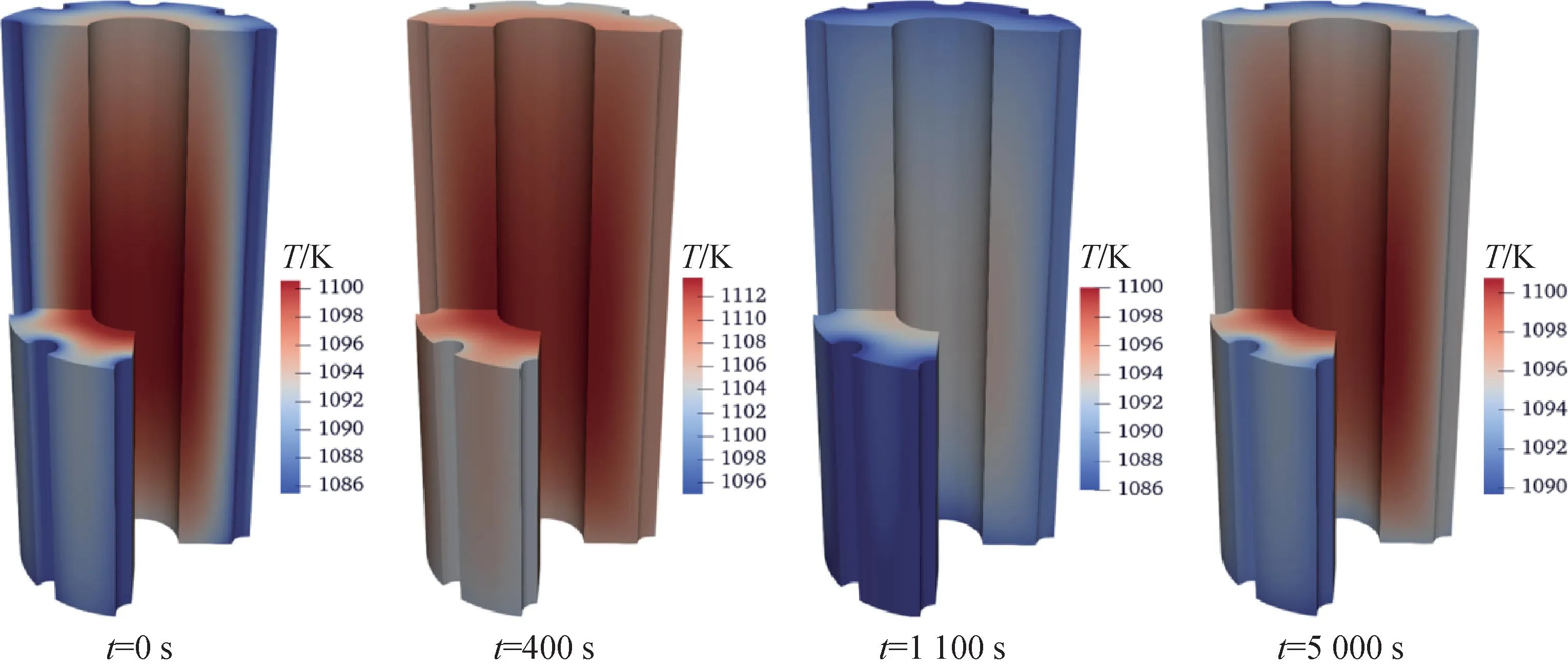
图15 主动冷却丧失工况下堆芯燃料温度场分布随时间的变化Fig.15 Fuel temperature distribution under active heat removal condition

4 结论

本文以温差热电转换型空间热管堆电源为主要研究对象,针对电源最主要的系统(包括堆本体、高温热管、温差热电转换系统)建立了基于OpenFOAM的三维堆本体多域传热模型、界面传热模型、堆芯功率模型、反应性反馈模型,并建立了高温热管模型、温差热电转换模型,结合高效的数值求解算法,开发了适用于温差热电转换型空间热管堆电源系统瞬态分析程序。采用文献参数及试验数据,分别就高温热管和温差热电转换模块进行了验证,结果与参考值和试验值符合较好。温差热电转换模块在两组测试温度工况下,发电功率计算值与试验值最大相对偏差在2.75%以内。采用本程序对KRUSTY反应堆进行建模分析,分别开展了负荷跟踪、热电转换模块失效、反应性引入、主动冷却丧失工况下的瞬态分析,计算结果充分体现了KRUSTY非能动的传热特性和较好的抗单点失效能力。与试验数据的对比表明,在上述工况下堆芯功率与试验值符合较好,燃料的温度与试验值最高偏差不超过4.1 K,验证了程序的准确性。程序将为后续温差热电转换型空间热管堆电源瞬态分析提供有效的分析手段。