基于有限体积法碱金属高温热管冷态启动流动换热数值研究

赵昊城,张泽秦,王成龙,秋穗正,田文喜,苏光辉

(西安交通大学 核科学与技术学院,陕西 西安 710049)

热管作为一种非能动热传输装置,主要通过工质相变传热,可以自发运行,输送工质不需要额外的能量输入,是一项广泛应用的创新型输热元件[1],热管具有极高的热导率及良好的等温性,能够在传热的同时保持加热段和冷凝段温度几乎均匀[2]。为在高温环境中长期稳定运行,高温热管常选用碱金属作为传热工质[3]。由于高温热管工作温度较高,且工质多为化学性质活泼的碱金属,实验研究工作难度较大[4],为此国内外学者提出不同的启动模型对碱金属热管冷态启动进行模拟。Cao等[5]提出采用自扩散模型描述蒸气区自由分子流态流动特性;Tournier等[6]开发了适用于碱金属热管的冷态启动分析模型HPTAM,是目前认可度最高的启动模型,HPTAM完整考虑了吸液芯结构带来的多孔介质阻力项和惯性阻力项,建立了吸液芯的完整动量方程,对于蒸气区采用尘气模型来模拟自由分子流、过渡流及连续流动[7]。Hansel等[8]基于MOOSE有限元框架,采用一维建模两相可压缩流动模拟,基于两流体七方程推导热管控制方程,对吸液芯部分液相流动采用达西方程描述。国内方面,Zhang等[9-10]开发了基于有限元方法的热管冷态启动三阶段模型。目前,国内的热管数值研究大多忽略了吸液芯部分流动,国际热管数值模拟中吸液芯部分流动相关研究资料较少并缺乏验证。

本工作针对高温碱金属热管启动阶段工质传热和流动进行研究,使用有限体积法(FVM)建立热管瞬态分析模型,开发热管瞬态模拟程序,对单根水平钠热管冷态启动过程进行数值模拟,分析热管温度和压力分布以及蒸气各项参数变化,研究环境温度和绝热段长度对热管启动特性的影响。

1 数学物理模型

考虑热管为轴对称的圆柱结构,选取合适的特征长度,进行轴向和径向的二维板型计算域简化,控制区域如图1所示。图1中:Qin为蒸发段外界输入功率;Qout为冷凝段与外界换热功率;l为热管整体长度;le、la和lc分别为蒸发段、绝热段以及冷凝段长度。对该模型主要做出以下假设:1) 忽略热管中工质受到的体积力;2) 不考虑蒸气区中不凝气体的影响;3) 热物性仅为温度的函数;4) 蒸气为一维层流流动。

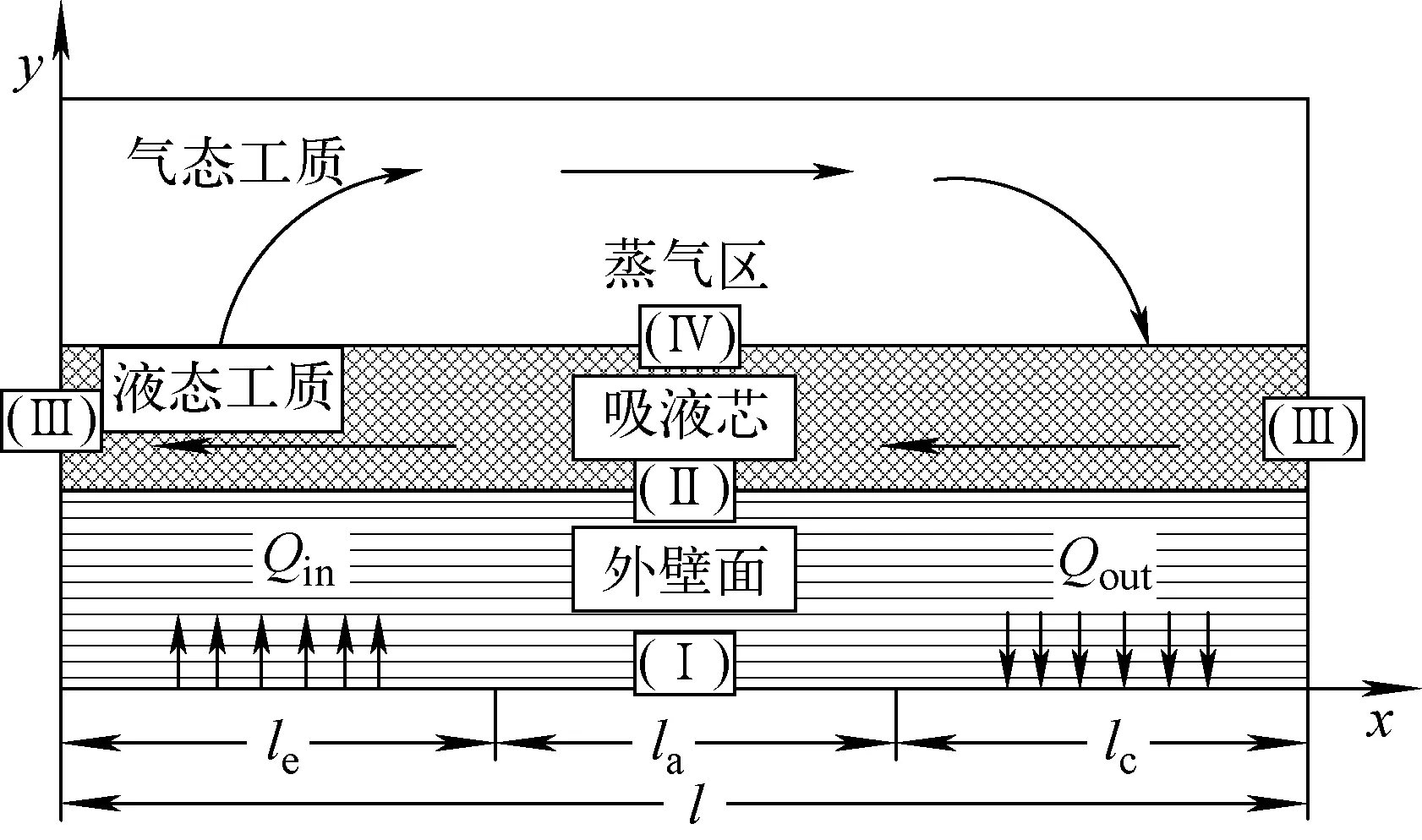
图1 热管模型示意图Fig.1 Schematic diagram of heat pipe model

1.1 管壁传热模型

外壁区传热过程使用笛卡尔坐标系中的热传导方程[11]描述,控制方程为:

(1)

式中:t为时间;x、y分别为轴向和径向方向;(ρwacp)wa为管壁体积热容;Twa为管壁温度;kwa为管壁导热系数。

1.2 吸液芯多孔介质流动换热模型

吸液芯内工质流动的连续方程为:

(2)

式中:ε为吸液芯多孔介质孔隙率;ρwf为液相工质密度;u和v分别为轴向和径向温度。

采用达西方程[12]模拟吸液芯内部工质流动:

(3)

式中:μv为液态工质动力黏度系数;K为多孔介质渗透率;p为吸液芯内相对压力分布;u为液态工质流速。

吸液芯内能量方程为:

(4)

式中:Twi为吸液芯内热平衡温度;(ρcp)eff为吸液芯等效体积热容;keff为等效导热系数。

等效物性参数由Chi模型[13]计算,具体计算方法为:

(ρcp)eff=ε(ρcp)wf+(1-ε)(ρcp)wi

(5)

(6)

式中:(ρcp)wf为工质体积热容;(ρcp)wi为吸液芯材料体积热容;kwf为工质导热系数;kwi为吸液芯材料导热系数。

吸液芯内部方程中速度均为流体通过整个多孔介质区域的速度,即表观速度[14]。

1.3 蒸气区域模型

根据传质学研究[15],克努森数Kn常用于表征蒸气自由分子态与连续态的转变阈值。热管处于冷态时,蒸气区压力很小,根据Kn定义,此时Kn应是一个很大的值,表明气体分子间相互作用影响小于气体分子与孔隙壁面碰撞产生的影响,随着热管操作温度的上升,Kn逐渐减小。本文定义Kn=0.01为转变阈值,即当Kn<0.01时认为蒸气区进入连续流动状态。

(7)

式中:λ为蒸气分子平均自由程;D为热管蒸气区直径。

蒸气自由分子态与连续态的转变阈值可由Kn[16]得到:

(8)

式中:M为相对分子质量;D为蒸气空间宽度;Ru为理想气体常数;μ为蒸气动力黏度系数;ρ为蒸气密度。

自由分子态时计算忽略蒸气区和气液界面,随温度升高,蒸气区中出现连续流动部分,并随热管启动时间增加逐渐扩展,连续流动部分与自由分子部分分隔界面称为连续锋面,连续流态下认为蒸气处于准稳态运行状态,当热管蒸气区到达该状态时,采用文献[16]中给出的一维可压缩稳态层流流动控制方程进行模拟。这是因为在该阶段虽然热管温度仍在继续上升,但蒸气区内蒸气流动状态变化十分缓慢,可使用稳态方程进行处理。在计算控制方程中所需的摩擦因子、动量因子和能量因子时,由于热管蒸气区的通道宽度大于高度,视为二维模型进行处理,且在一个面上存在与该面法向方向相同的注入流速,与半多孔介质通道特征相同,因此采用文献[17]中半多孔介质通道相似解进行处理。

1.4 边界条件

热管各边界所使用的边界条件不同,各部分边界具体划分如图1所示。

1) 热管沿轴向划分为蒸发段、绝热段和冷凝段,这3部分边界条件分别设定恒定功率输入边界、绝热边界和对流换热边界:

(9)

式中:hc为外壁面与环境等效换热系数;Tamb为环境温度;qin为蒸发段外部热流密度。

2) 管壁与吸液芯之间主要通过导热的方式进行传热,忽略工质流动造成的对流换热。

3) 热管轴向两端均设为绝热边界条件,吸液芯部分添加无滑移边界条件:

v=0x=0和x=l

(10)

4) 根据蒸气的不同流态,吸液芯与蒸气区界面采用不同边界条件。当蒸气处于自由分子态时,认为气液界面绝热;处于过渡流态时,根据气体动理论[18]得到界面质量流量。忽略蒸气区能量和质量的累积,并综合考虑声速极限的限制[19]。

未达到声速极限

(11)

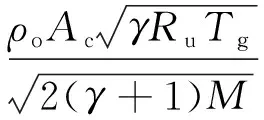
(12)

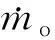
吸液芯区和蒸气区通过气液界面能量方程进行耦合计算:

(13)

式中,kwv为吸液芯中气液界面导热系数,定义为吸液芯区域在气液界面上的导热系数,在计算过程中根据界面温度和物性关系式进行计算。

气液界面边界上流速与界面质量通量满足:

(14)

2 程序开发及验证

采用FVM,基于C语言环境开发了高温热管启动瞬态分析程序HPWF。对热管管壁及吸液芯部分分别进行二维建模,使用矩形网格进行划分,如图2所示。

图2 程序网格划分Fig.2 Program grid division

2.1 程序数值方法

在划分的控制容积中心[11]设置节点,为避免求解出“棋盘式”压力分布,采用交错网格[11];分别选取合适的松弛因子,使用超松弛迭代法求解管壁和吸液芯部分压力方程和能量方程;使用牛顿迭代法求解气液界面能量守恒非线性方程;蒸气区参数的常微分方程组通过4阶龙格-库塔法进行求解。

2.2 程序验证

首先进行程序网格无关性验证。研究对象设置为长1 m的热管,对于长径比较大的热管,轴向网格划分对计算结果影响较大,因此在管壁径向上划分2层网格,吸液芯径向上划分4层网格,在轴向上分别划分25、40、50和67层网格进行计算,选取蒸气区最高温度和计算时间作为对比参数。程序网格无关性验证结果如图3所示。当网格数量从300增加到402时,蒸气区最高温度变化很小,而计算时间增加25.7%,计算成本大大增加,因此选择轴向划分50层网格、网格数量300作为计算工况。

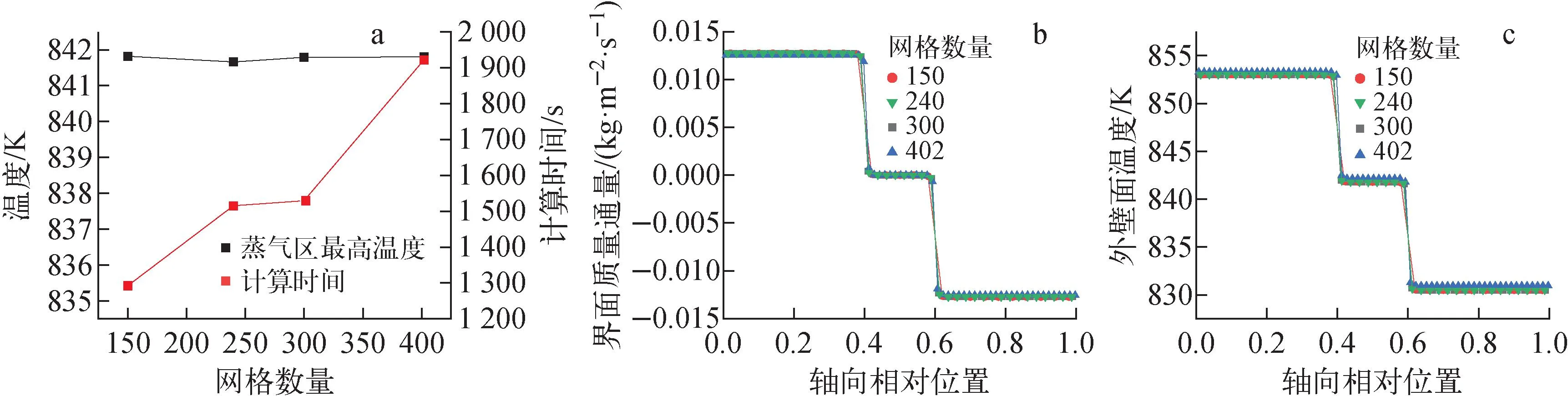
a——蒸气区最高温度和计算时间分布;b——气液界面相变质量通量分布;c——热管外壁面温度分布图3 程序网格无关性验证Fig.3 Program grid independence verification

为验证HPWF程序对热管启动瞬态分析的正确性和准确性,选用Lee等[20]测试的钠热管实验数据进行验证。实验采用长为1 m的钠热管,使用可变电压器控制加热功率,冷凝段外壁使用空气自然对流冷却,将6个K型热电偶装入小型屏蔽管,插入热管中心以测量蒸气温度。实验采用热管的具体参数列于表1。

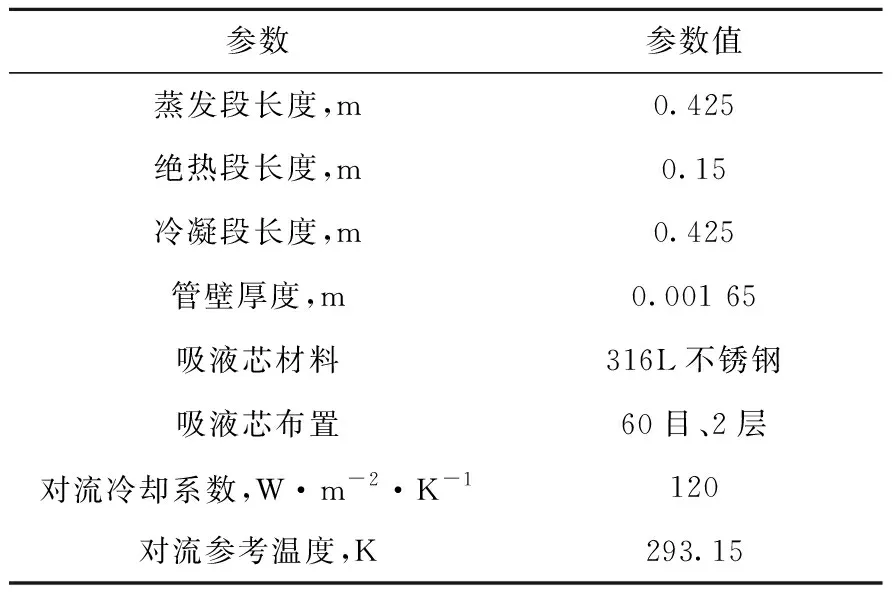
表1 钠热管结构参数Table 1 Structure parameter of sodium heat pipe

热管启动过程中,蒸气温度变化与稳态蒸气温度分布的模拟结果与实验数据对比如图4所示。由图4可见,模拟结果与实验数据符合较好,最大相对误差约为9.8%。

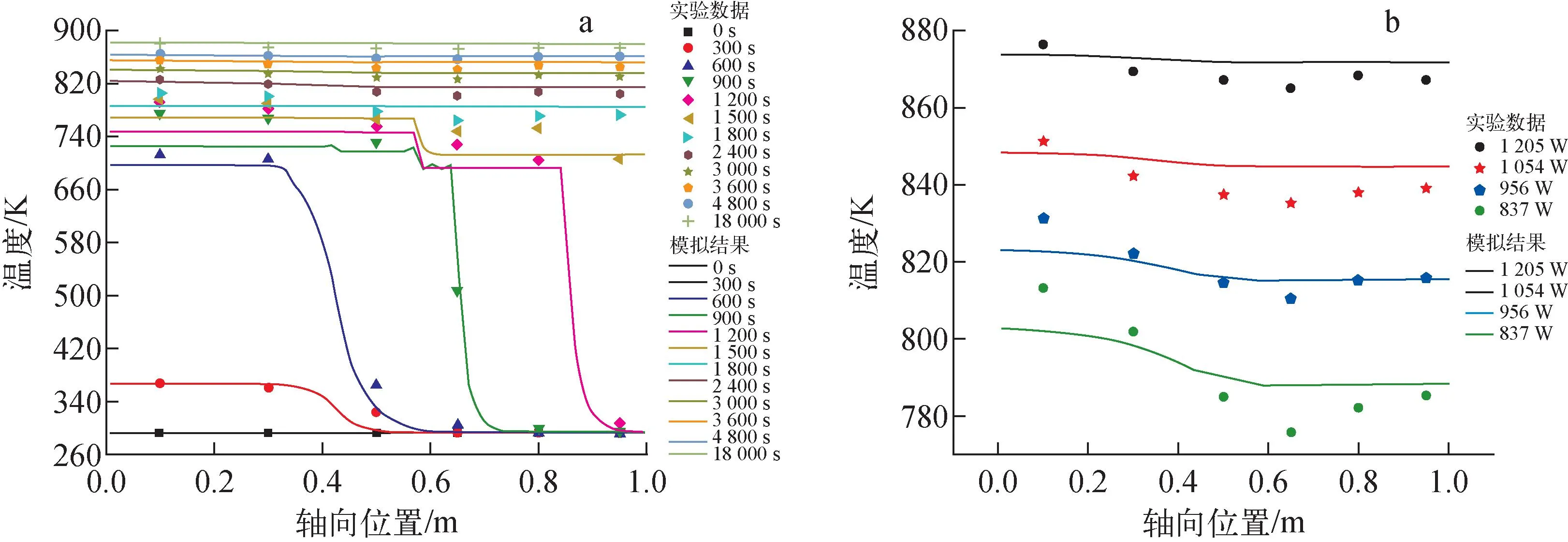
a——启动瞬态;b——稳态运行图4 模拟结果与实验数据的对比Fig.4 Comparison of simulation result and experimental data

3 计算结果

对单根水平钠热管冷态启动瞬态过程进行计算分析,热管蒸发段长为0.4 m,绝热段长为0.2 m,冷凝段长为0.4 m,热管外径为30 mm,管壁厚度为4 mm,吸液芯厚度为2 mm,材料为316L不锈钢,蒸发段外壁面边界热流为定常输入,输入功率设定恒定的1 000 W,换算热流密度为53 051.65 W/m,冷凝段外边界换热系数设为100 W/(m2·K)。

3.1 启动特性分析

图5示出热管冷态启动壁面温度轴向分布。启动总用时3 000 s,壁面轴向温差最终稳定在22 K。由于各段给定边界条件均匀,启动阶段任一时刻蒸发段,以及初始阶段和准稳态稳态运行阶段绝热段、冷凝段温度分布均匀。

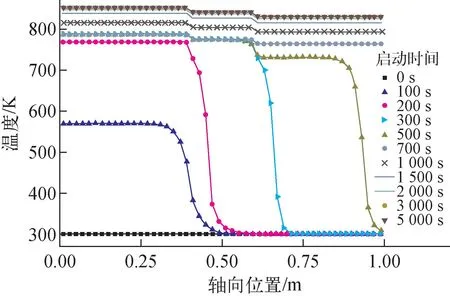
图5 壁面温度轴向分布Fig.5 Axial distribution of wall temperature

启动开始时蒸发段温度快速升高。t=200 s时,连续锋面进入绝热段,轴向温度分布曲线上出现了很大的温度梯度;t=300 s时,绝热段整体温度到达776 K温度平台,连续锋面进入冷凝段,热管整体的温度曲线呈三阶梯式分布,蒸发段与冷凝段连续流区域的温差仍较大,约为60 K;t=600 s后,温度曲线分布形状不再发生改变;t=800 s时,轴向最大温差维持在稳定值。连续流动锋面在冷凝段移动过程中,已到达连续流态的冷凝段部分平台温度略有下降,下降幅度约为15 K,这是由于冷凝段升温过程中,轴向传热量被限制在较低的声速极限并保持不变,而程序假设换热系数为较大的定值,当冷凝段升温区域增加时,外界环境换热量增大导致冷凝段温度降低。

图6示出热管启动过程中蒸气区理想热流和声速极限随时间的变化。在t=150～700 s阶段,实际传热受到声速极限限制。t=570 s之前,热管的理想热流量上升速度很快;当t=570 s时,热管的理想轴向热流量达到最大值14 090.3 W,而此时声速极限将传热量限制在600.1 W;t=570～720 s时,理想热流量迅速下降,此阶段蒸气区整体达到连续流态,冷凝段气液界面温度快速升高,直到热管整体温差保持恒定。

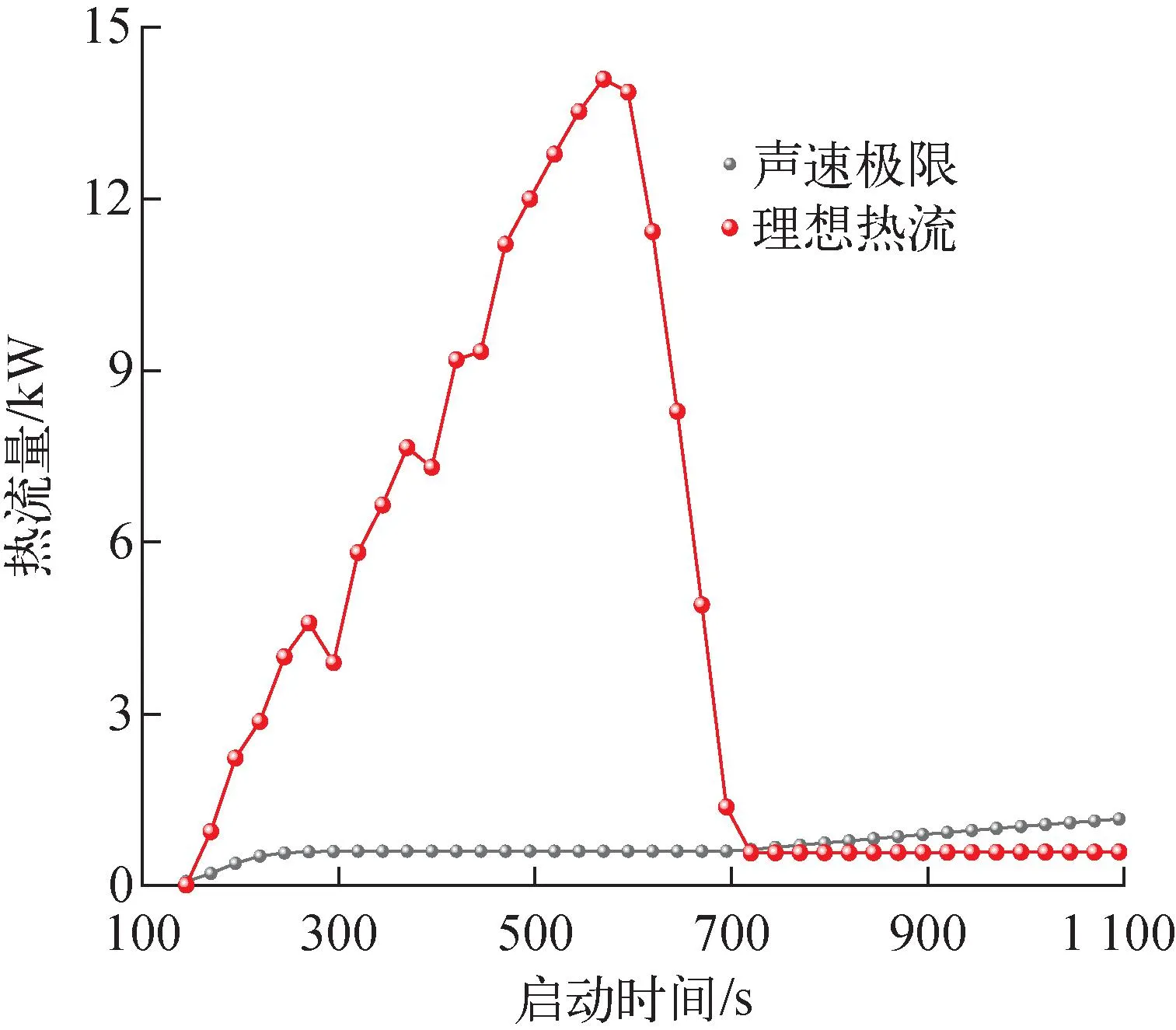
图6 理想热流与声速极限的变化Fig.6 Variation of ideal heat flux and limit of sound velocity

图7示出熔化前沿与连续锋面相对位置随时间的变化,熔化前沿是指吸液芯中固液交界面所在的位置。t=50 s时,熔化前沿出现在蒸发段与绝热段交界面上;t=150 s时蒸气区中出现连续流动区域,连续锋面开始沿轴向推进。热管轴向热流受到声速极限限制,熔化前沿和连续锋面沿轴向以恒定速度推进,第2阶段末期(t=400～650 s),推进速度略有降低,最终在t=600 s和t=650 s时熔化前沿和连续锋面先后到达冷凝段末端,热管进入准稳态运行阶段。

图7 熔化前沿和连续锋面位置的变化Fig.7 Position variation of melting front and continuous front

设置蒸发段端部压力为0作为参考压力,图8示出吸液芯内部压力相对值分布。由图8可见:热管吸液芯径向压力变化不到1 Pa,轴向压力梯度较大,稳态压降可达到47 Pa;当连续锋面到达冷凝段末段后,吸液芯整体压降达到最大值,启动继续进行,整体压降约7.73 Pa,这是因为工质的动力黏度系数随温度升高而降低,相同速度条件下压力梯度略有降低。

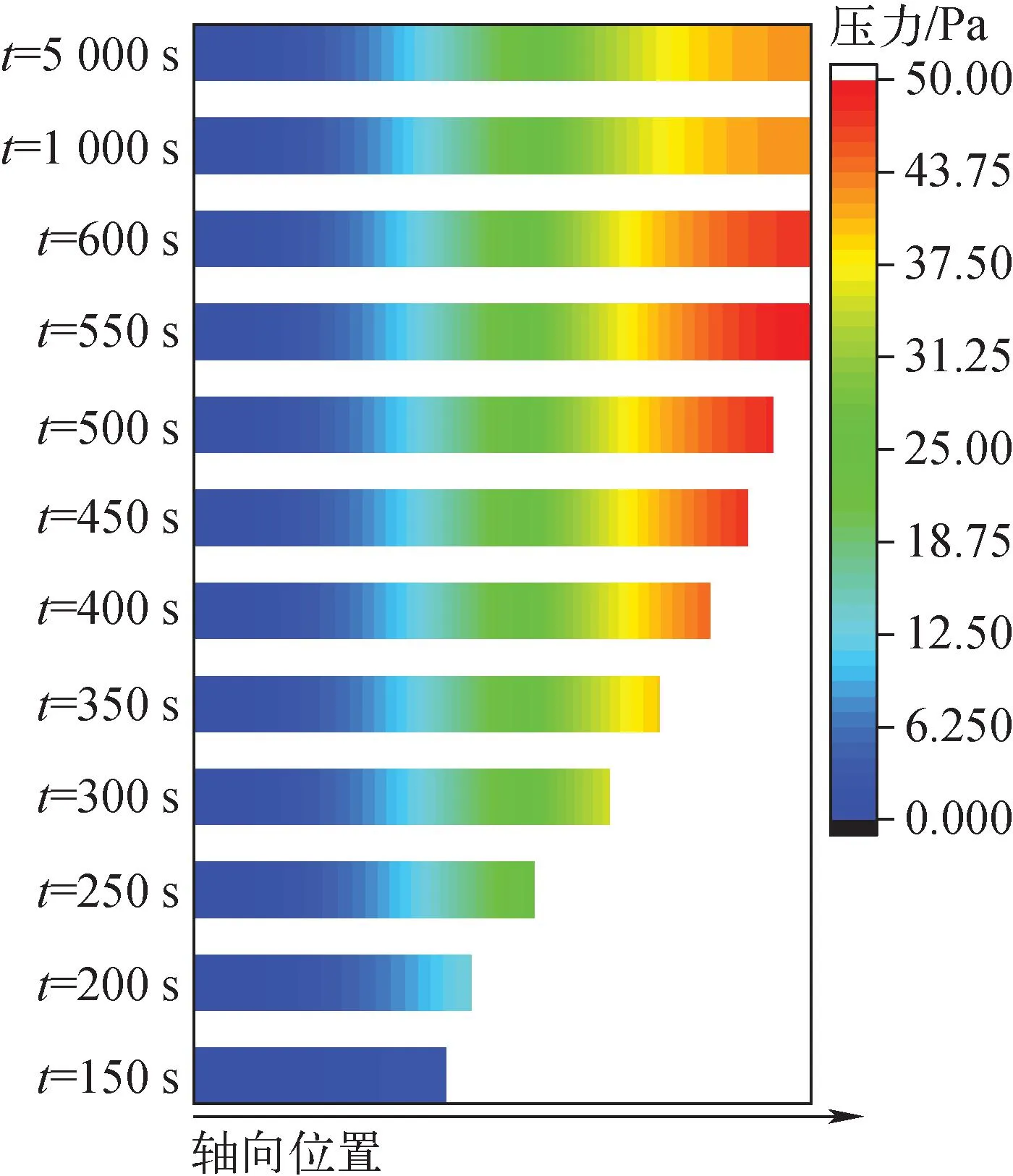
图8 吸液芯压力的变化Fig.8 Variation of pressure of wick

图9示出吸液芯稳态流速分布。由图9可见,径向流速很小,最大流速仅为0.01 mm/s,冷凝段末端径向流速很大,达到6 mm/s。由达西方程可知,在吸液芯渗透率很小的情况下,一个很小的压力波动会引起流速巨大变化,而吸液芯内部流速变化对温度分布的影响很小,因此实际上压力和温度分布都无明显变化。绝热段处流体的轴向流速绝对值最大,速度剖面呈梯形,而最大轴向速度也仅约3 mm/s。图9中负流速表示液相流动方向与轴向方向相反,轴向速度梯度为0.007 5 s-1。

图10示出蒸气区完全进入连续流态后不同时刻热管蒸气各项参数分布。在相变质量的累积引起的蒸气流加速压降和摩擦压降共同作用下,蒸发段中蒸气压力急剧下降,温度下降幅度也达到最大,约为3.8 K;绝热段中由于摩擦压降作用,压力近似线性下降,且温度继续降低,由于钠蒸气膨胀引起密度减小,流速和马赫数略有增加;冷凝段中蒸气相变引起的质量损失导致速度降低,而摩擦压降的影响始终存在,因此压力无法完全恢复。

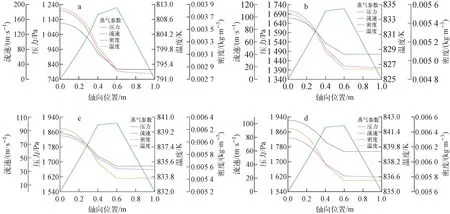
a——启动1 112.40 s;b——启动1 785.60 s;c——启动2 418.20 s;d——启动4 993.20 s图10 热管蒸气参数的变化Fig.10 Variation of steam parameter of heat pipe

3.2 环境温度敏感性分析

表2列出环境温度对热管启动运行特性的影响。由表2可见,环境温度降低10 K,稳态工作温度也下降约10 K,完全启动时间缩短约50 s。

表2 环境温度对运行特性的影响Table 2 Influence of ambient temperature on operating characteristics

不同初始温度稳态蒸气压力和流速的分布如图11所示。由图11可见,钠蒸气压力随环境温度增加而增大,蒸气流速随环境温度增加而降低,这是因为钠蒸气密度随温度升高而迅速升高,界面相变量保持恒定,导致蒸发段流速增大幅度下降。

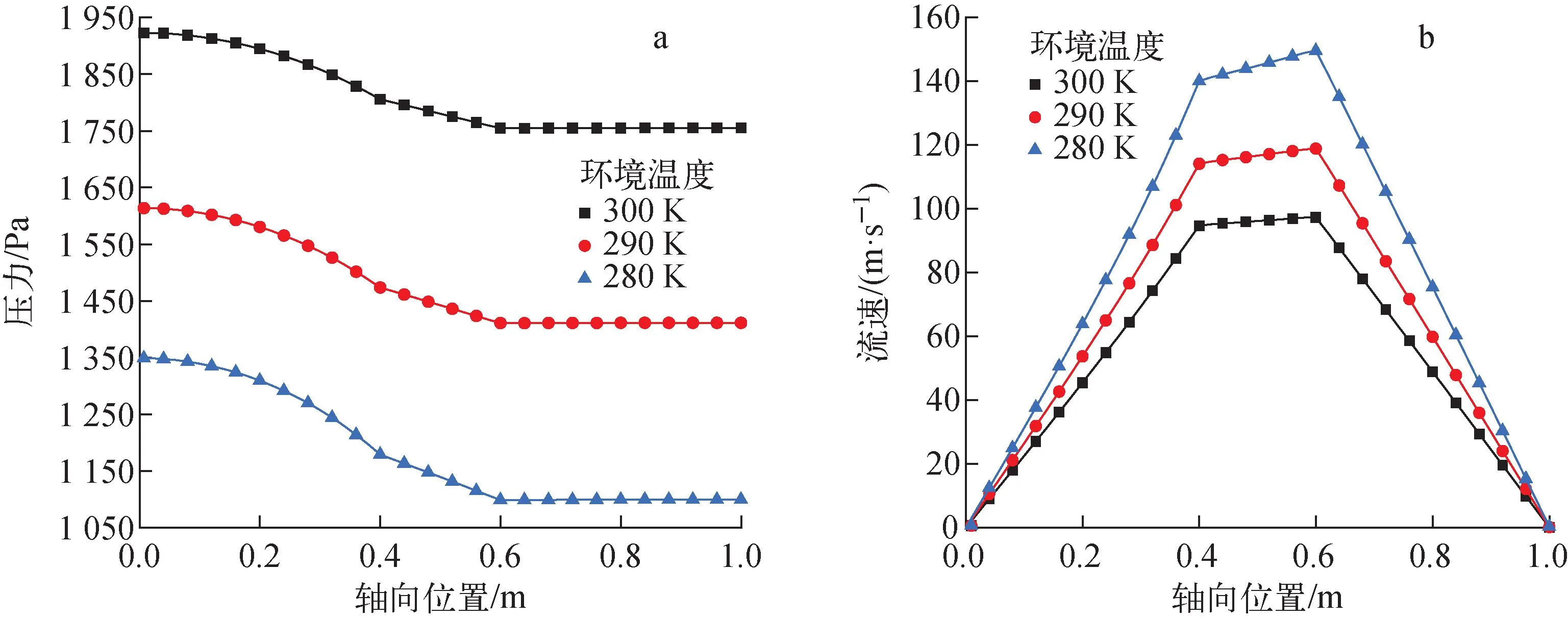
图11 稳态蒸气参数分布Fig.11 Distribution of steady state steam parameter

3.3 绝热段长度敏感性分析

表3列出不同绝热段长度下热管启动运行特性。随绝热段长度增加,热管启动时间延长,气相压降和液相压降增加,工作平均温度相等。

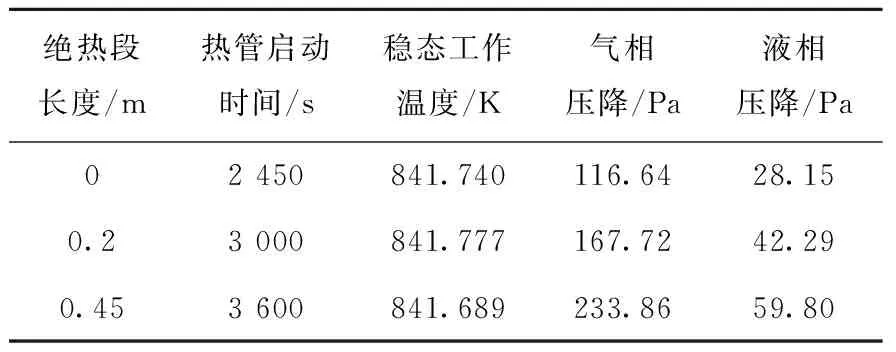
表3 绝热段长度对运行特性的影响Table 3 Influence of insulation section length on operating characteristics

不同绝热段长度下稳态液相压力和轴向流速分布如图12所示,图12中负流速表示液相流动方向与轴向方向相反。由图12a可见,蒸发段和冷凝段流速变化相同,而绝热段液相流速不变。这是因为液相不可压缩,密度保持不变,因此界面质量通量相同的情况下,流速不发生变化,因此绝热段长度并不影响液相最大流速以及蒸发段和冷凝段的速度变化趋势。由图12b可见,3种热管液相压力分布形状一致,且蒸发段和绝热段压力变化形状相同,而绝热段压降随长度增加对应线性增加。

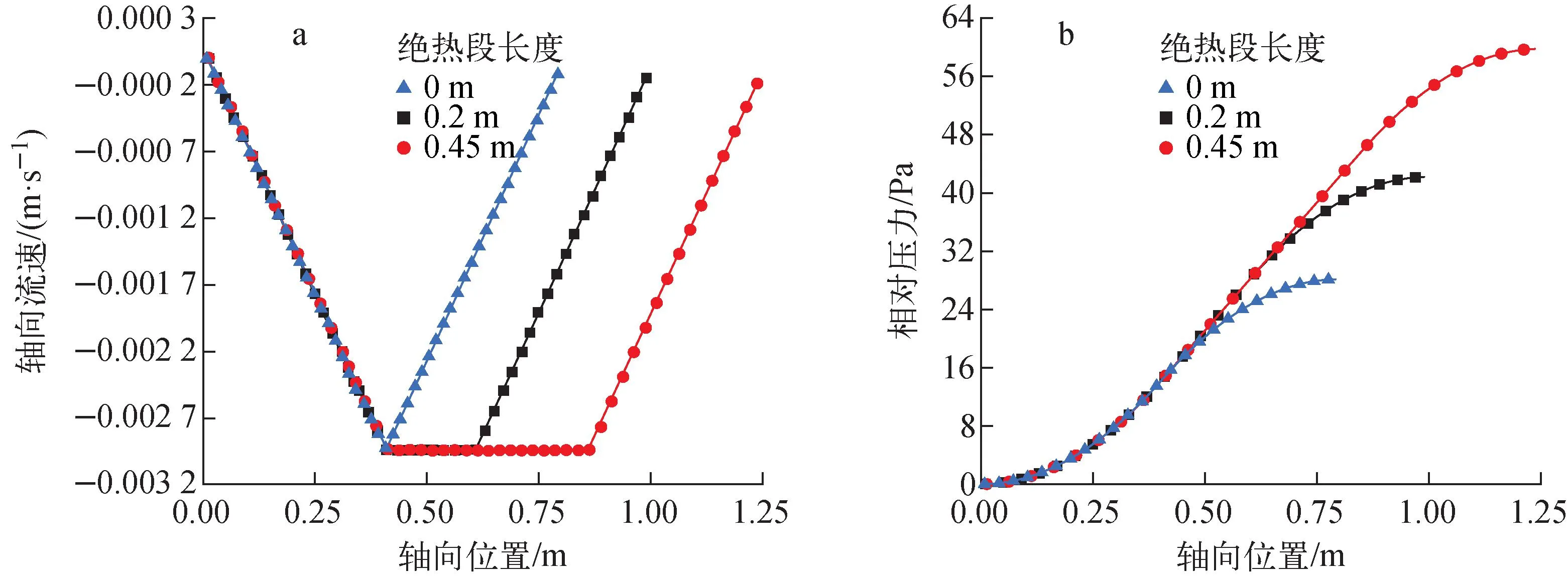
图12 吸液芯稳态参数分布Fig.12 Parameter distribution of steady state of wick

4 结论

本文提出的模型采用Kn划分热管启动不同阶段,并采用达西方程描述吸液芯中液态工质的流动,对于蒸气区采用准稳态一维可压缩层流假设建立控制方程。本文建立了热管启动模型并开发了热管冷态启动瞬态分析的HPWF程序,使用公开文献实验数据验证程序,最大相对误差约为9.8%。本文模拟研究了高温钠热管启动过程中吸液芯压力变化,并分析了启动阶段蒸气各项参数的分布及变化关系,得到的主要结论如下。

1) 热管冷态启动过程中,温度分布整体呈现为三阶梯式,外壁面轴向温差先增大后减小,最大温差达到了487 K,到达稳态后工作温度约为841.777 K,壁面温差约为22.51 K。

2) 吸液芯内部压力相对值随工质熔化部分的扩展而增大,最大轴向压降达到50 Pa,当工质完全熔化后,轴向压降随温度升高略有降低,最终稳态工况下轴向压降稳定在47 Pa。

3) 在蒸气区部分处于连续流态时,热管受到声速极限限制,轴向传热量很小,当整体到达连续流态时,蒸气温度快速升高,气液界面温差迅速减小,最终突破声速极限。

4) 环境温度升高使得热管稳态工作温度升高,启动时间延长,蒸气区整体绝对压力升高,最大流速增加,但对轴向温差无明显影响;绝热段长度增加延长了热管启动时间,使得吸液芯和蒸气区内压降增大,而对稳态工作温度和外壁面轴向温差影响较小。