光伏系统中虚拟惯性与阻尼增益协调控制策略

何润泉，陈槾露，陈俊安，张峻诚，赵军，潘凯岩，3

（1.广东电网有限责任公司茂名供电局，广东茂名 525000；2.东方电子股份有限公司，山东烟台 264000；3.哈尔滨工程大学 智能科学与工程学院，黑龙江哈尔滨 150000）

0 引言

电力电子器件广泛应用于可再生能源系统中，使电力系统的动态响应特性发生了显著变化，由此引发了电力系统的稳定性问题[1，2]。新能源发电系统具有更高的灵敏性和更快的响应速度，大电网无法单纯依靠传统火力发电机组的转子加速或减速来吸收或者供给电网多余能量以平衡系统惯性，从而将电网的频率控制在稳定范围内。因此，以光伏等新能源为主导的发电机组也需要纳入到一次调频任务中，快速地调节频率，以缓解火力发电机组频繁的调峰、调谷压力，维持整体电力系统的稳定性[3]。

为了解决光伏发电的间歇性问题，可以通过使用储能系统、需求侧响应、虚拟惯性等技术[4，5]来调节可再生能源发电厂和风力/光伏发电场向电网输送的能量频率。文献[6]提出了一种有功备用式光伏虚拟同步发电机控制策略，可以在不增加额外储能的情况下使光伏具有调频的功能。文献[7]利用储能优势弥补光伏动态特性的不足，实现了独立微网的频率稳定。文献[8]为了模拟虚拟惯性，修改了PV系统中的直流链路电压控制，通过f-Upv和f-Udc补偿环节影响频率的暂态过程，达到稳定频率的效果。文献[9]提出了双级式光伏发电有功功率-频率下垂控制和虚拟惯量控制，通过修改Boost变换器或网侧逆变器原有的控制结构，实现光伏发电主动参与电网频率调节。文献[10]提出了一种代替传统光伏逆变器的同步功率控制器，其在任何情况下都不需要改变控制结构[11]。然而，上述这些解决方案没有考虑到系统的阻尼作用，以及未充分发挥光伏系统的功率调节能力，而且额外的储能设备增加了电网投资。

为充分发挥光伏本身的功率调节能力并且考虑到系统中阻尼的影响，本文提出了一种针对光伏系统中虚拟惯性控制和频率阻尼控制的协调策略，将传统同步发电机中惯性常数和阻尼增益的调节特性有机结合，旨在光伏系统具备一定功率储备情况下实现最佳频率调节。最后，通过仿真验证了所提出的控制策略的优势和有效性。

1 光伏系统及其相关控制

典型的两级三相光伏控制系统如图1所示。图中：Cpv，Cdc为直流滤波电容；ipv，upv分别为光伏阵列侧直流电流、直流电压；Lf为滤波电感；PCC为并网点；iPCC，uPCC分别为并网点电流、电压。光伏阵列板输出直流电先经过Boost升压变换器升压后再通过网侧逆变器将交流电输送至大电网中，由锁相环（PLL）实现同步控制功能。通常情况下，光伏系统的输出功率由升压变换器调节，一般采用最大功率跟踪（MPPT）算法。注入电网的有功和无功功率由网侧逆变器调节，一般采用双环电流控制策略。在MPPT基础上增加有功储备可以实现各种灵活的有功功率控制方案，例如功率储备控制、功率限制控制等。此外，还可以实现频率控制，包括虚拟惯性控制（VIC）和频率阻尼控制（FDC）。

图1 光伏系统结构框图Fig.1 Structure diagram of photovoltaic system

2 光伏系统有功备用运行机制及功率储备的选择

传统光伏系统通过MPPT算法进行控制以最大化能量产出，在此过程中光伏系统始终在最大功率点（MPP）运行。为了实现光伏系统自适应地调节输出功率，光伏系统保留一定数量的储备功率是必要的，其算法和模式会相应地改变，因此需要对具有功率储备的MPPT控制进行分析。

光伏面板在25℃水平下的功率-电压（P-V）曲线如图2所示。从图中可以看出，随着电压的增加，功率先增加后减小，在P-V曲线上产生一个拐点（MPP）。通常情况下，通过实时功率储备控制策略测量最大光伏功率（P），为了实现功率储备（Pres），光伏系统应在功率储备点（PRP）而不是MPP处运行。非单调的P-V关系将会存在两个功率储备点，即左功率储备点（L-PRP）和右功率储备点（R-PRP），分别对应于MPP的左侧和右侧的功率储备点。由于MPP右侧的斜率大于左侧斜率，在R-PRP处响应更快，同时在MPP左侧提升有功功率备用容量需要降低直流母线电压，斜率较缓意味着直流电压需要更大的压降，会导致光伏存在脱网风险。因此，通常采用R-PRP进行光伏系统的功率储备操作[12]。

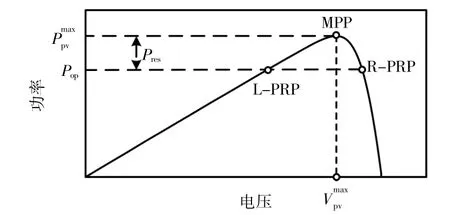
图2 功率-电压曲线Fig.2 P-V curve

在考虑功率储备时，由于R-PRP调节速度较快，当辐照度突然下降时，光伏电压可能会跃升超出开路电压，同时考虑到光照强度较低时功率储备较低，一次调频效果不佳，所以本文采取分段储备方式，其数学模型如下：

式中：Pmpp为最大功率；σ为功率储备系数；Ppv为光伏实时运行功率；Pmin为最小功率，应根据当地光照水平设定，一般取额定容量的10%；S为光照强度。

3 电网频率质量与调节

频率是考察设备与电网是否同步的一个关键参数。在电网规范中，频率质量要求是最基本的，不同容量和电网管理标准下制定的频率质量要求可能会有所不同，我国规定电网频率为50±（0.2～0.5）Hz。

如图3所示，以频率降低时的频率动态情况为例，当发生负荷突然增长或事故（例如发电机停机）时，频率下降导致相对较大的频率变化率（RoCoF）（通常在给定的时间窗口内测量）。在检测到事故后，启用一次调频控制，频率将在达到最低点后逐渐增加；频率将在新的稳态周围震荡，表明频率已恢复，此时稳态频率远离其名义值；激活二次调频控制，系统控制中心将重新分配每个发电机组的输出功率参考值，频率开始在正常操作范围内逐渐增加；最后，频率恢复正常。

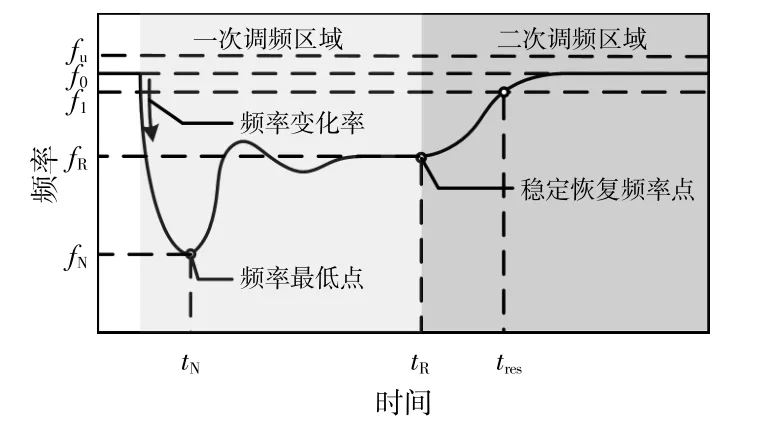
图3 频率降低时的频率动态情况Fig.3 Frequency dynamics during an under-frequency issue

图3中，频率稳定指标包括频率最低值fN（频率下降时）、稳态恢复频率fR（或者稳态频率偏差f0-fR）、RoCoF和恢复一次调频响应时长tres。由于主频率控制只能由发电机组独立实现，而次级频率控制由整个系统的控制中心执行，与主频率控制相关的频率稳定指标是区域发电机组最需要考虑的。因此，在设计光伏系统的电网频率支持控制时，应关注fN，RoCoF和fR。

传统电网频率稳定由同步发电机的转子调节实现，其中机械惯性和阻尼决定了频率特性。为了正确设计光伏系统的虚拟惯性控制（VIC）和频率阻尼控制（FDC），首先需要研究摆动方程的机制。摆动方程可以表示为

式中：H为惯性常数；ω为角频率；Pm为机械功率；Pe为电磁功率，Pe=Kδ，其中，δ为功角，K为同步力矩系数；D为阻尼增益；ωs为系统额定角频率。

摆动方程可以用传递函数框图表示，如图4所示。由图4可以看到，惯性常数H和阻尼增益D决定了有功功率和频率的动态特性。具体而言，H主要决定频率的导数（RoCoF），D更多地影响频率偏差（f0-fR）。在大规模电力系统中，RoCoF高度依赖系统的总惯性，而f0-fR更多地依赖系统的总阻尼。为了进一步说明H和D对频率动态的影响，进行以下分析。

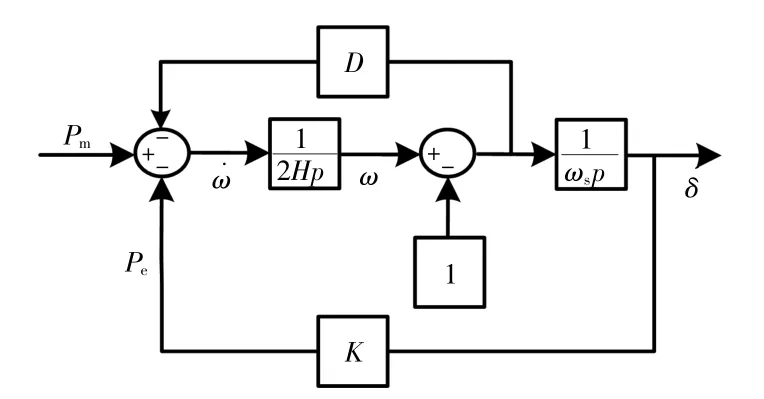
图4 同步发电机转子运动方程框图Fig.4 Diagram of equations of motion of synchronous generator rotor

①惯性常数

H从0～2 s增加到10 s时，负载突变25%情况下频率和RoCoF的响应如图5所示，其中D固定为5 p.u.。

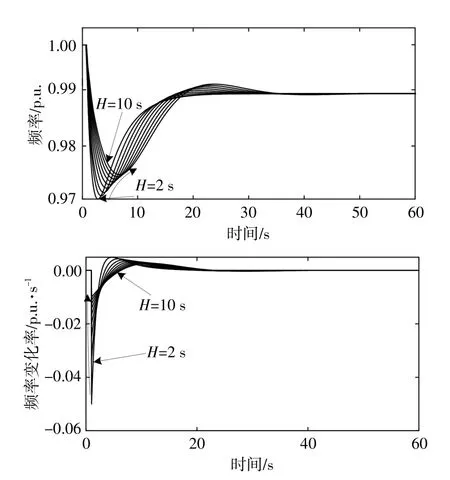
图5 不同惯性常数下频率和频率变化率的动态情况Fig.5 Dynamic behavior of frequency and frequency rate of change under different inertia constants

从图5可以看出，在达到恢复频率之前，频率会出现一段时间的振荡。当H增加时，频率谷值显著增加，达到谷值的时间也相应增加。在达到谷值后，频率上升恢复到额定值，直至达到上升拐点（RoCoF为零）。值得注意的是，H不会影响恢复频率，因为惯性在瞬态能量中起到缓冲作用，该能量在达到新的稳态后将减小为零。从图5中还可以看到，随着惯性的增加，RoCoF得到有效降低，避免了由于较大的RoCoF引起的多种紧急情况，例如发电机组的脱网，从而提高了频率质量，进一步改善了系统稳定性。

②阻尼增益

在H为6 s的情况下，D从2 p.u.增加到10 p.u.，本文进行了类似的研究，结果如图6所示。从图6可以看出，随着D的增加，频率谷值增加，而达到谷值的时间相应减小。值得注意的是，较大的D可以有效抑制后续振荡（较小的过冲），频率将更快地恢复到之前状态，恢复频率更接近额定值，可以减轻系统中其他发电机组的调节负担。从图6还可以看出，在频率谷值之前，D几乎不会影响RoCoF，而在振荡过程中，RoCoF通常是最大的。尽管在频率谷值之后增加D可以减小RoCoF，但对于改善频率质量而言，其影响相对较小。

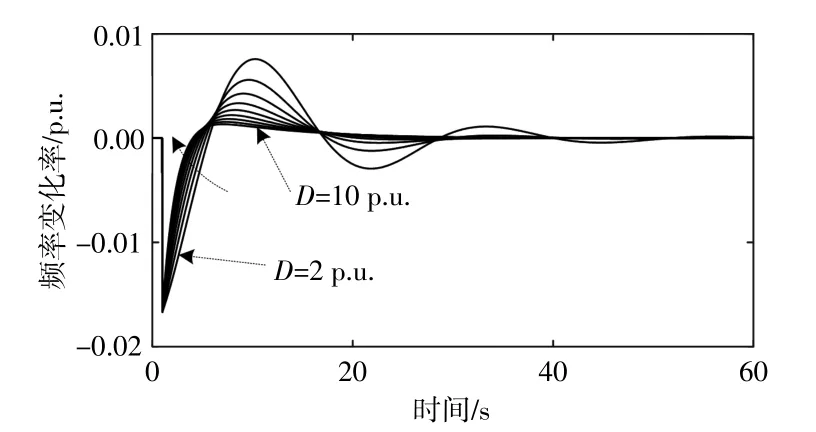
图6 不同阻尼增益下频率和频率变化率的动态情况Fig.6 Dynamic behavior of frequency and frequency rate of change under different damping gains

从以上分析可以得出结论，较大的H可以增加谷值并减小RoCoF，而D对于增加频率谷值（较大的谷值）和f0-fR贡献更大。

4 光伏系统中虚拟惯性和频率阻尼协调控制

受到同步发电机转子摆动方程特性的启发[式（1）]，光伏系统的频率控制可以通过VIC和FDC两个方面实现，旨在增强电网的惯性和阻尼。对于同步发电机而言，其惯性和阻尼特性由转子的机械属性确定，这是不可改变的。然而，与同步发电机不同，光伏系统可以借助电力电子技术更灵活地调节输出功率，为电网提供适应性的惯性和阻尼，从而有效提高电网的频率质量。为此，本文提出了一种新的光伏系统频率控制策略，在一定功率储备下以最佳方式协调VIC和FDC，实现频率最佳控制。

4.1 VIC和FDC

如前文所述，为了实现VIC，光伏系统的输出功率应与RoCoF成比例调节，即：

式中：Hpv为光伏系统的虚拟惯性。

FDC可以通过光伏输出功率与f0-fR成比例调节实现。

角频率ω与频率f之间的关系为ω=2πf。当f，ω取标幺值时，ω=f。

所以式（3）和式（5）可以写为关于f的表达式，即：

4.2 具有一定功率储备情况下的协调控制

频率低点、频率变化率和稳定频率偏差是频率质量的关键指标。RoCoF通常在频率事件的早期阶段达到最大值。对于光伏系统的频率控制，低频事件的目标是降低RoCoF，特别是在振荡的早期阶段，增加频率可能达到的低点值，并保持恢复频率接近额定值。通过增加H，可以有效降低振荡早期阶段的RoCoF，并增加低点。尽管较大的D也可以增加低点，但对于扰动的早期阶段RoCoF几乎没有影响。至于恢复频率（t时刻的频率与额定频率偏差，即稳定频率偏差），它不受H的影响，可以通过较大的D保持在较高水平。因此，为了改善频率质量，在频率事件的早期阶段应采用较大的H，而在低点后则希望采用较大的D。然而，在光伏系统中，虚拟H和D受可用调节功率的限制，为了最大化光伏系统的频率支持能力，应根据上述讨论适当协调功率储备。具体而言，当检测到异常频率时，激活频率调节。此时，功率储备用于产生虚拟惯性，其中H被设置为H；一旦检测到频率低点，功率储备用于提供频率振荡的阻尼，D应为D，而H为零。为了进一步说明光伏系统如何相互协调实现频率波动后自适应控制，本文将频率以及RoCoF作为判断特征量，通过两个S-R触发器检测、触发以及生成逻辑信号。

图7为频率自适应控制在各个频率场景下的逻辑控制情况。

图7 频率发生波动后控制逻辑Fig.7 Control logic after frequency fluctuations

①如图7（a）所示：当频率处于稳态频率[通常在（50±0.2）Hz]之内，频率波动检测S-R触发器Q输出为0，同时频率导数接近于0，监测装置输出布尔变量为1；控制切换中S-R触发器Q输出为0，反信号!Q输出为1，此时系统在阻尼控制下运行。

②如图7（b）所示：当频率发生波动后（该时段指最低点前），频率波动检测S-R触发器Q输出为1，频率导数不为0，输出布尔变量为0；由于①中频率波动检测S-R触发器Q输出的布尔变量为0，而频率发生波动后频率波动检测S-R触发器Q输出的布尔变量为1，触发上升沿，此时控制切换中S-R触发器输入S布尔变量为1，输入R布尔变量由1变成0，没有触发上升沿，因此布尔变量为0，系统频率由虚拟惯性控制。

③如图7（c）所示：当频率达到最低点时（该时间是瞬时的），频率波动检测S-R触发器Q输出仍然为1，但是没有触发上升沿，控制切换中S-R触发器输入S布尔变量为0；频率导数此时为输出布尔变量1（最低点导数为0）；控制切换中S-R触发器输入R布尔变量由0变成1，触发上升沿，输入R布尔变量为1，系统频率由阻尼控制。

④如图7（d）所示，当频率开始恢复时（该时段指最低点后和达到恢复稳态频率之前），频率导数不为0，输出布尔变量又变为0。但输入至控制切换中S-R触发器前的上升沿均没有收到0-1的触发信号，因此系统频率仍然由阻尼控制。

⑤当频率恢复至稳态频率后，频率和频率变化率的输出布尔变量又为1，等待下一次频率波动事件的发生。

上述所形成的S-VIC和S-FDC布尔变量信号将在升压转换器的PWM控制中实现，如图8所示。光伏输出功率参考是通过最大可用功率、功率储备和VIC或FDC引入的额外参考生成的。功率参考与瞬时输出功率之间的差异将被发送到比例积分（PI）控制器，然后生成升压转换器的占空比。VIC和FDC环路的激活由各个频率状态下所生成的切换信号控制。

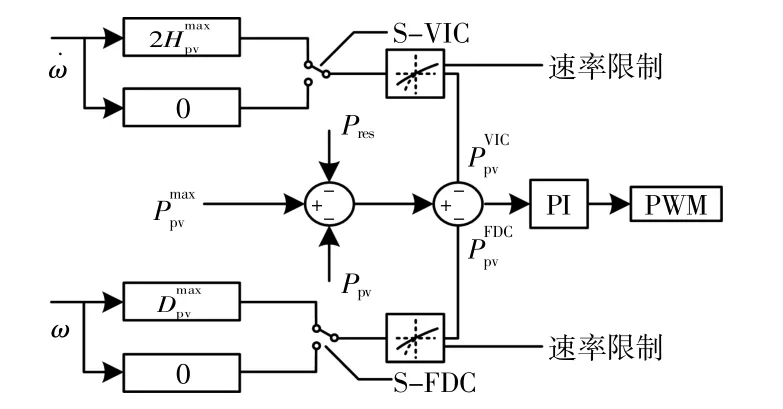
图8 三相桥式逆变器主电路拓扑Fig.8 Main circuit topology of the three-phase inverter

5 仿真验证

5.1 光伏系统在不同控制策略下负荷增加时的频率响应

在t=1 s时，光伏系统施加了2 MW的负载变化。光伏系统在不同控制策略下（无控制、固定虚拟惯性常数控制、固定阻尼增益控制和协调控制）的频率动态如图9所示。当光伏系统未采用任何频率控制时，频率下降至49.27 Hz，振荡后达到恢复频率49.40 Hz。在这种情况下，测得负载变化后0.2 s时RoCoF为-1.27 Hz/s。通过固定阻尼增益控制，频率的最低点和恢复频率显著提高，RoCoF略有降低；相反，通过固定惯性常数控制，RoCoF显著降低。尽管频率最低点提高了，但性能不及固定阻尼增益控制。此外，恢复频率根本没有增加，这意味着光伏系统在振荡后不支持电网频率。

图9 光伏系统在不同控制策略下负荷增加时系统频率响应曲线Fig.9 Frequency response curve of photovoltaic systems under different control strategies during load increase

当采用本文提出的控制策略时，在振荡的早期阶段，虚拟惯性常数控制发挥作用，频率动态与固定惯性常数控制的情况相似。RoCoF降低，最低点提高。此外，由于光伏系统在最低点后切换到固定阻尼增益控制，恢复频率显著增加。更重要的是，恢复频率甚至高于固定阻尼增益控制的情况。原因是本文提出的控制策略中D是由最大稳态频率偏差计算得出的，而固定D是由最大瞬时频率偏差计算得出的。

从图9（b）中可以看出，在本文提出的控制策略下，最低点后的RoCoF比其他控制方法的大。这是由虚拟惯性常数控制切换到固定阻尼增益控制所引起的。然而，由于H和D的变化速率受到一定程度的限制，这个阶段的RoCoF要比振荡的早期阶段小得多，符合电网规范要求。

从图9（c）中可以看出，通过固定惯性常数控制，在振荡的早期阶段，光伏系统增加了输出功率，但在振荡后又恢复到初始点，这意味着光伏系统停止了对电网的频率支持。通过固定阻尼增益控制，光伏系统可以在振荡后继续支持电网频率。然而，由于对阻尼增益的限制，光伏系统无法利用所有的功率储备维持振荡后的电网频率。当采用本文提出的控制策略时，光伏系统在振荡的早期阶段增加输出功率以抑制频率最低点。与固定惯性常数控制不同，提出的控制策略使光伏系统再次增加输出功率，以实现更大的恢复频率。与固定阻尼增益控制相比，提出的控制策略充分利用了光伏系统的功率储备，在频率振荡后支持电网，使稳态频率偏差更小。

5.2 光伏系统在不同控制策略下负荷减少时的频率响应

在原系统参数下，光伏系统在t=1 s时负载减少2 MW的系统频率响应曲线如图10所示。

图10 光伏系统在不同控制策略下负荷减少时系统频率响应曲线Fig.10 Frequency response curve of photovoltaic systems under different control strategies during load reduction

如图10（a）所示，与光伏系统在负荷增加时频率调节特性相同，在频率事件早期阶段，采用固定虚拟惯性常数控制减缓系统频率上升速度，在达到最高点后，控制策略切换至固定阻尼增益控制以实现最小稳定频率偏差。固定惯性常数控制在最高点之前与协调频率控制表现相同，而最高点之后无法实现最小的稳定频率偏差。固定阻尼增益控制虽然也能尽快达到最低点，但该控制策略是由最大瞬时频率偏差计算得出的，最终调节效果没有协调控制明显。在协调控制下，光伏输出功率可以进一步被限制减小偏差，固定虚拟惯性常数控制在达到最高点后终止了频率调节，而固定阻尼增益控制由于无法完全利用功率储备而导致稳定频率仅维持在一定水平。

从两个案例的研究中可以得出结论，本文提出的控制策略有效地协调了虚拟惯性常数控制和固定阻尼增益控制，避免了二者单一控制的不足。因此，光伏系统的调节能力得到最大化，并且频率质量得到了很大程度的改善。

本文使用不同控制策略的频率质量指标总结如表1和表2所示。可以看出，本文提出的控制策略可以实现全面的最优频率质量。具体而言，只有固定阻尼增益和协调控制可以获得较大的最低点/较小的最高点，而只有固定惯性常数控制可以实现较小的RoCoF。更重要的是，通过本文提出的控制策略，稳态频率偏差最小，表明光伏系统的功率储备得到了充分利用。

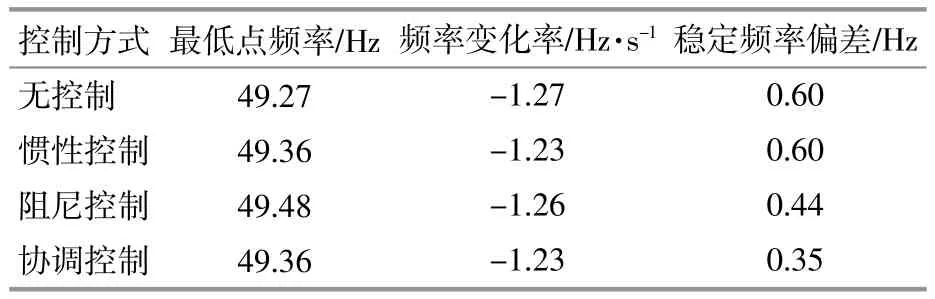
表1 不同控制策略下频率增加时各项指标Table 1 Various indicators when frequency increases under different control strategies

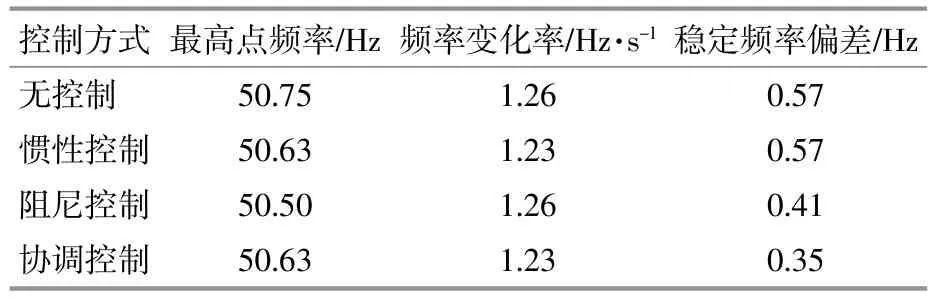
表2 不同控制策略下频率减少时各项指标Table 2 Various indicators for frequency reduction under different control strategies

6 结束语

本文提出了一种光伏系统具备功率储备的虚拟惯性与阻尼增益协调控制方法。该方法在电网频率波动的情况下，首先启用虚拟惯性控制减缓频率变化率并提高频率的最低点。一旦频率达到最低点后，光伏系统将切换至阻尼增益控制，以增加恢复频率。使电网中频率质量的3个关键指标（频率变化率、瞬时频率偏差和稳态频率偏差）得到最大程度上的优化，与现有的光伏系统单独虚拟惯性或单独阻尼增益控制相比，本文提出的控制策略能够最大化地利用光伏系统的功率储备，从而以一种经济高效的方式改善电网频率质量。