含T接逆变型分布式电源配电网的自适应距离保护
赵建文,张鸿波,胡雨佳
(西安科技大学 电气与控制工程学院,陕西 西安 710600)
0 引言
为了实现“碳中和”“碳达峰”的战略目标,可再生能源发电得到了重视与应用,大量的逆变型分布式电源接入配电网。分布式电源可以专线或T形方式接入系统[1]。逆变型分布式电源T形接入配电网后,配电网潮流方向与短路电流大小均发生变化,导致传统三段式保护适应性变差,保护的可靠性与灵敏性无法得到满足。
为了适应含T形接入的IIDG配电网,目前主要有两类保护方案。一类是对差动保护做出各种改进。文献[2]针对逆变型分布式电源T形接后的配电网提出了一种改进纵联差动保护方案。文献[3]针对含有T形接入IIDG配电网提出了一种复合阻抗差动保护,动作门槛值较大,当内部故障时可能拒动。文献[4]提出了基于幅值比的纵联保护,并在含有TT形接IIDG的情况下做出改进。文献[5]利用各类电流幅值信息构造了充分式判据,需要采集多种电流信息。此类保护方案需要实时获取线路首末两端以及DG出口处电气信息并进行数据交换,对通信系统要求较高,并且通信存在一定的延时,例如实时性最好的快速报文仍有着数毫秒的延时;除此之外,由于配电网网络复杂,通信网络规模巨大,需要大量的投资[6]。另一类是在传统三段保护的基础上提出了自适应保护。文献[7,8]在传统电流保护的基础上,针对IIDG接入的配电网提出了一种自适应电流速断保护。文献[9]针对高DG渗透率的配电网提出了一种自适应过电流保护方案。文献[10]提出了自适应的三段式距离保护,需要实时检测并网点电压,并且精度有限。文献[11]针对IIDG接入配电网后提出了一种延时距离保护与电流保护相结合的方法,保护构成较为复杂。这类方案仅使用保护本地信息,动作速度快,但是如何正确计算DG电流是保护正确动作的关键。
本文针对含有T形接入的IIDG配电网,在传统距离保护的基础上提出了一种自适应距离保护。该保护方法实时预测IIDG输出电流并用于整定计算,无需与远方通信,设备投资少,动作速度快,并且在不同的故障条件下均有较高的保护范围,通过与传统距离保护的对比,证明了该保护方法的优越性。
1 逆变型分布式电源输出特性分析
并网运行的IIDG一般采用PQ控制,通过双闭环控制有功功率和无功功率的输出恒定。如果在派克变换中令d轴与电压矢量同方向,可得到功率输出[12]的表达式为
式中:Up为公共连接点(Point of Common Coupling,PCC)线电压;Id,Iq分别为IIDG有功参考电流和无功参考电流。
接入配电网的IIDG应具备一定的故障穿越能力[1],在并网点电压较低时,主要输出无功功率以支撑并网点电压。故障期间IIDG输出的无功电流Iq为
式中:Us为并网点电压标幺值;IN为IIDG额定电流;K1与K2为低电压穿越控制策略的支撑系数,一般K1不小于1.5,K2不小于1.05。
因此,在系统发生三相短路时,IIDG输出电流由PCC电压决定,等值为PCC电压控制的电流源。此外,为了改善系统发生不对称故障时IIDG的输出特性,IIDG采用正序分量的控制策略,在配电网发生不对称故障时,IIDG仍然只输出正序故障电流,此时IIDG等值为PCC正序电压控制的电流源[13]。
2 T接IIDG对传统距离保护的影响
相较于三段式电流保护,距离保护基本不受系统运行方式的影响,有着更优秀的保护性能。然而由于IIDG的T形接入,将导致距离保护的保护范围降低。图1为配电网拓扑结构,分析IIDG以T形接入后对距离保护的影响。
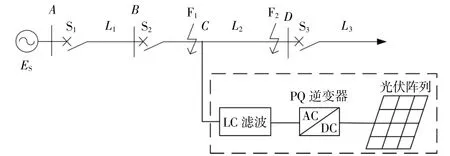
图1 含T接IIDG的配电网结构图Fig.1 Distribution network structure diagram including T-connected IIDG
当IIDG发生三相短路时,得到系统电路如图2所示。
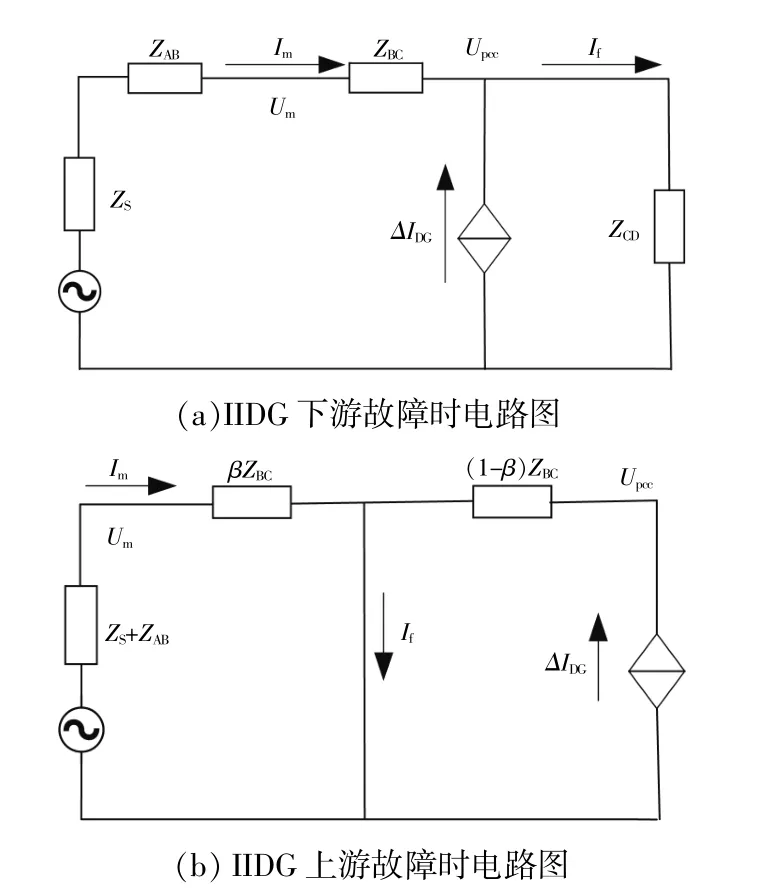
图2 不同位置故障系统电路图Fig.2 Circuit diagram of fault system at different positions
由图2(a)可得保护S2处的电压为U˙m=I˙mZBC+(I˙DG+I˙m)ZCD。因此,保护S2处的测量阻抗为
如果不考虑可靠系数,则距离保护S2的整定值为线路BD的阻抗,即:
由于距离保护为欠量保护,当测量阻抗小于整定值时,保护动作。对比式(3),(4)可知,由于IIDG输出电流的影响,测量阻抗会增加一附加阻抗,当该附加阻抗与线路阻抗相角差小于90°时,将会导致Zset<Zm,保护无法正确动作,保护可靠性变差。
下面分析IIDG以T形接入后距离保护的保护范围与IIDG渗透率之间的定量关系。假设IIDG容量为SDG,系统电源的容量为SS,IIDG渗透率为x%,则根据渗透率的定义可以得到:
式中:US与IS分别为系统电源的额定电压与电流;UDG与IDG分别为IIDG的额定电压与电流。
由于IIDG处于并网状态,因此US≈UDG,根据式(6)可得:
由式(8)可以看出,距离保护的保护范围在不考虑可靠系数的情况下,已经无法保护线路全长,并且随着IIDG渗透率的增加,保护范围会进一步减小。此时保护范围外的故障需要在一定的时限以后才能切除,这不利于电力系统的安全稳定运行。
当故障发生在IIDG上游时,β为故障点到线路首端占线路BC的比例,此时保护S2处的测量电压为U˙m=βI˙mZBC,测量阻抗为因此,当IIDG上游发生故障时,IIDG不会影响距离保护的正常动作。
3 自适应距离保护
由前文分析可知,由于T形接IIDG的输出电流的影响,传统距离保护的保护范围减小,保护可靠性与灵敏性变差,并且IIDG的输出电流受故障位置与控制策略的影响,具有很大的不确定性。如果按IIDG的额定电流进行保护值的整定也同样不合理,因此有必要提出适用于各种情况的自适应距离保护。
3.1 三相短路
为了正确反应各种相间短路故障,阻抗继电器采用0°接线,由于三相对称,以反应A相故障的继电器为例,接入继电器的电压为U˙m=U˙AB,电流为I˙m=I˙A-I˙B。当IIDG上、下游线路末端发生三相短路故障时,阻抗关系如图3所示。

图3 阻抗关系示意图Fig.3 Schematic diagram of impedance relationship
当IIDG下游线路末端发生三相短路故障时,可得A相与B相电压为
因此,保护处的测量阻抗为
由于故障发生在IIDG下游,系统电流I˙A与IIDG输出电流I˙DGA均从上游流向下游的短路点,K为正,ZBD与KZCD两者相角差小于90°。当IIDG上游发生三相短路故障时,系统电流I˙m从上游流向短路点,而I˙DG则从下游流向上游的短路点,K为负。因此,ZBD与KZCD两者相角差大于90°。如果仍按式(10)计算整定值,则阻抗整定值偏小,Zset<ZBD,当DG输出的电流较大,甚至有可能Zset<Zm,从而导致保护的拒动。而由前文分析可知,当故障发生在IIDG上游时,传统距离保护不受影响,可以正确动作。综上,可令自适应距离保护的整定值为

3.2 两相短路
IIDG下游发生AB两相短路故障时,其等效图如图4所示。
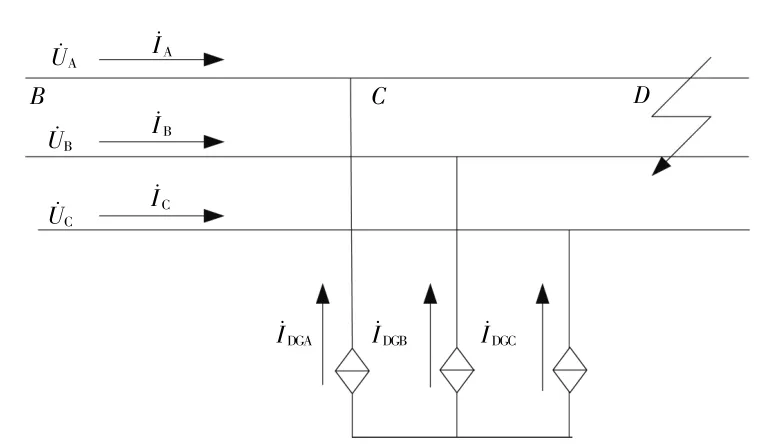
图4 两相短路示意图Fig.4 Schematic diagram of two-phase short circuit
由图4可得A相与B相电压为
同样,令U˙m=U˙AB,I˙m=I˙A-I˙B,可得保护的测量阻抗同式(9)。因此,两相短路距离保护的整定值与三相故障相同。不同的是,当发生AB两相短路时,由于U˙C=E˙C,将导致B相与C相的继电器不能正确反应保护处到故障处的阻抗,无法正确动作。
3.3 IIDG输出电流的实时计算
自适应保护可以根据系统当前的运行状态及故障类型,实时计算出被保护线路末端短路时的整定值,然后按照避开该整定值的原则对保护进行实时整定,因此具有更高的可靠性与灵敏性。为了实时获得IIDG的输出电流,如果在IIDG出口处加装电流互感器,并且将IIDG的电流实时传输至保护处,无疑增加了设备投资与通信负担。因此,利用保护处故障信息得到IIDG的输出电流成为关键。随着微控制器与微机继电保护技术的发展,电力系统处理数据的能力不断提高,本文提出了利用BP神经网络实时预测IIDG电流的方法,系统的整体硬件结构如图5所示。
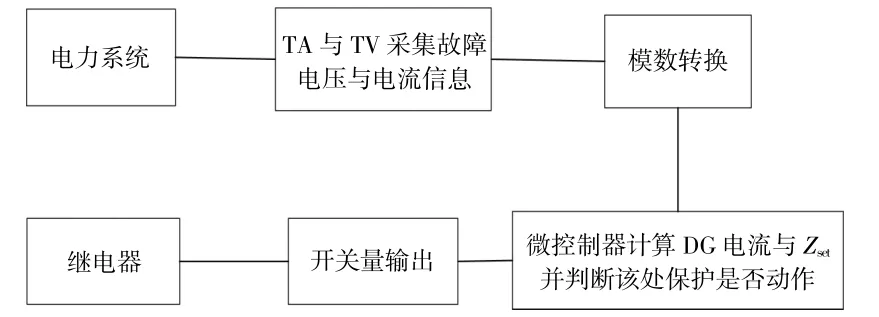
图5 自适应保护硬件结构图Fig.5 Hardware structure diagram of adaptive distance protection
由前文分析可知,IIDG在配电网发生三相短路时等效为受并网点电压控制的电流源,IIDG的电流为
由图2可知:故障发生在IIDG下游时,U˙pcc=U˙m-αI˙mZL2,I˙DG=f(U˙m,I˙m);故障发生在IIDG上游时,U˙PCC-I˙DGZL2=U˙m-I˙mZL2,同样可得I˙DG=f(U˙m,I˙m)。即无论故障发生在IIDG上游或下游,I˙DG都与I˙m和U˙m存在着一定的函数关系。但是,由于IIDG的控制策略复杂多变,难以通过一具体的函数公式表示该关系。由于神经网络能够无限逼近任意连续函数,因此使用BP神经网络对故障数据进行拟合,当故障发生时,利用训练好的神经网络实时预测IIDG的电流。
为了得到I˙DG与I˙m,U˙m间的关系,在IIDG上游与下游分别设置100次故障,选择95%的数据作为测试集训练神经网络。输入层节点数为5,分别为U˙m,I˙m的幅值与相位,DG容量5个变量作为BP神经网络的输入,输出层节点数为2,分别为IIDG电流的幅值与相位,隐藏层节点数根据经验值取3。在故障发生时,根据保护处的电气量信息实时预测IIDG的输出电流并代入整定公式中。DG容量为1 MW,不同位置发生三相故障的幅值与相位预测结果如图6所示。
由图6可以看出,神经网络可以较为准确地预测出IIDG的输出电流,最大幅值相对误差为1.12%,最大相角相对误差为1.37%。
当系统发生两相短路故障时,由于IIDG采用正序分量控制,仍然输出三相对称的电流,此时IIDG等效为受并网点正序电压控制的电流源,即:
式中:U˙pcc(1)为PCC电压正序分量。
因此,发生两相短路时,使用对称分量法提取U˙m和I˙m正序分量作为神经网络的输入。
4 仿真及结果分析
4.1 仿真系统及参数
本文在MATLAB中建立含IIDG的10 kV配电网拓扑模型,如图7所示。
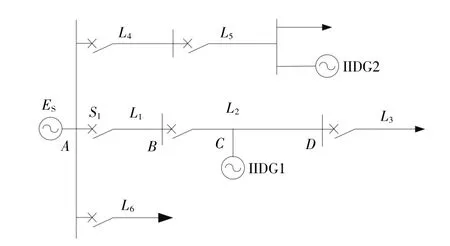
图7 含IIDG配电网结构Fig.7 Structure diagram of distribution network including IIDG
图中,线路阻抗Z=0.110 0+j0.163 3 Ω/km,线路L1~L5长度分别为5,10,5,5,3,3 km。负荷有功功率均为5 MW,各IIDG均采用正序分量的PQ控制及低电压穿越控制,其中IIDG2有功功率参考值为2 MW,IIDG1以T形接于距离线路首段25%处,有功参考值分别取1,4 MW,以验证不同容量的IIDG对保护的影响。阻抗继电器采用比幅式方向阻抗继电器,动作特性为
4.2 仿真结果
表1~4为自适应距离保护与传统距离保护的对比结果。
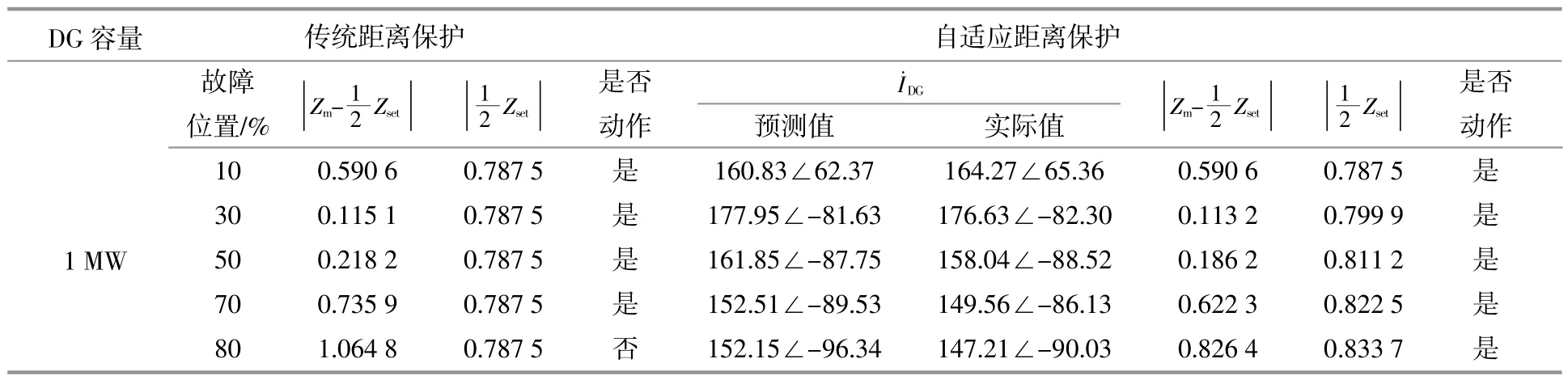
表1 自适应距离保护与传统距离保护的对比结果(ABC三相故障,DG=1 MW)Table 1 Comparison results of adaptive distance protection and traditional distance protection(ABC three-phase fault,DG=1 MW)

表2 自适应距离保护与传统距离保护的对比结果(ABC三相故障,DG=4 MW)Table 2 Comparison results of adaptive distance protection and traditional distance protection(ABC three-phase fault,DG=4 MW)
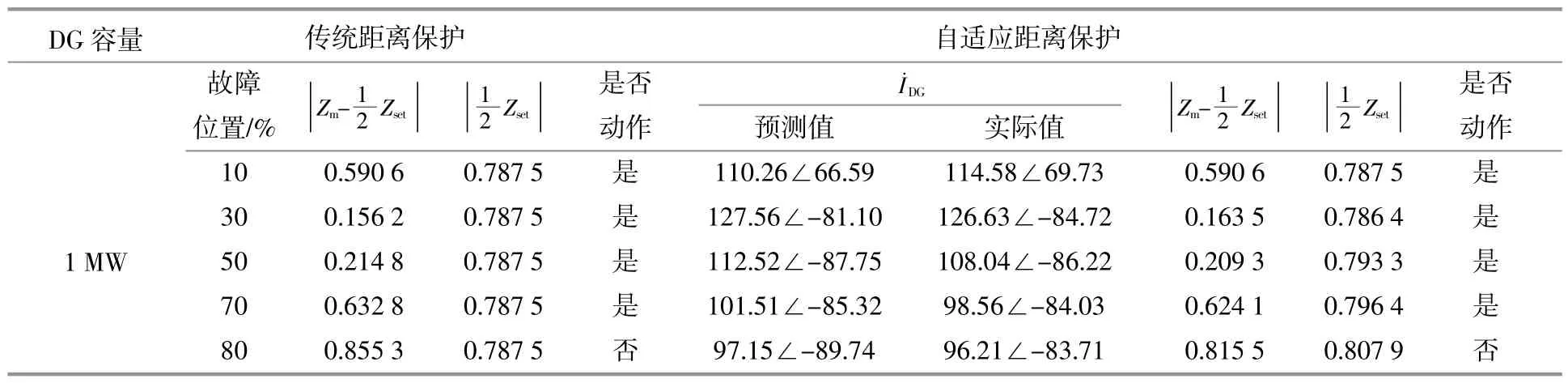
表3 自适应距离保护与传统距离保护的对比(AB两相故障,DG=1 MW)Table 3 Comparison results of adaptive distance protection and traditional distance protection(AB two-phase fault,DG=1 MW)
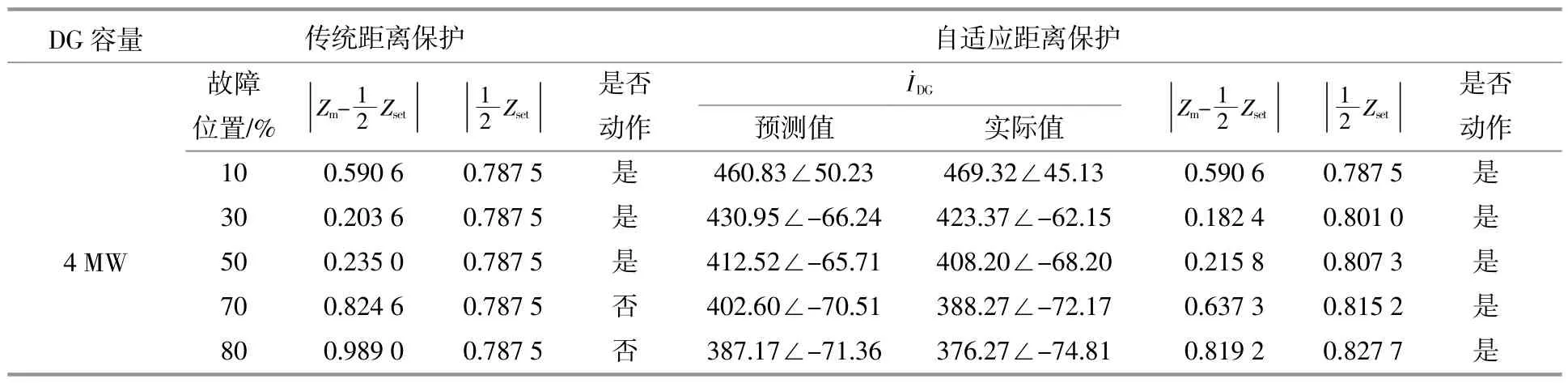
表4 自适应距离保护与传统距离保护的对比(AB两相故障,DG=4 MW)Table 4 Comparison results of adaptive distance protection and traditional distance protection(ABC two-phase fault,DG=4 MW)
通过仿真结果可以看出,由于IIDG的接入,传统距离保护的保护范围减小,且减小的程度与IIDG容量有关。因此,在IIDG下游部分线路发生故障时,传统距离保护将无法动作,无法满足保护的可靠性。而自适应距离保护在不同的条件下可以保护线路全长的80%左右,并且在IIDG上游发生故障时,自适应保护退出,不影响保护的正确动作。因此,本文提出的自适应距离保护与传统距离保护相比,有着更高的灵敏性与可靠性。
5 结论
针对大量IIDG接入配电网后,传统继电保护的不足,本文提出了一种自适应距离保护方案。该保护方案根据IIDG的输出电流,实时整定保护动作值,在最大范围内实现无时限切除故障;保护仅利用本地信息,保护速动性与经济性较好;保护范围基本不受故障类型与IIDG容量影响,保护可靠性较好。由于考虑了可靠系数,该保护方案仍无法保护线路全长,需要与距离Ⅱ段与距离Ⅲ段保护配合,整定方法类似。该保护方案有利于提高含IIDG配电网的供电可靠性,促进可再生能源就近消纳。

