TMD控制对15 MW单桩风力机地震动力响应的影响

余洁，秦志豪，杨阳

（宁波大学 海运学院，浙江 宁波 315211）

0 引言

我国东部沿海地区经济发达，电力需求旺盛，但由于目前国内仍以火力发电为主，传统化石能源的短缺已成为制约其发展的障碍。在此背景下，海上风电逐渐成为当地电力资源的重要组成部分。海上风力机仍以单桩、三角架和导管架等固定式基础为主，其中单桩以其技术最为成熟和安装简便等优点，成为近海风力机应用最为广泛的基础形式[1]。出于经济性的考虑，单桩式风力机正朝着大型化的方向发展，由此导致其结构柔性增强，同时也更易受地震激励影响[2]。

对于地震作用下的风力机动力响应，国内外学者开展了大量研究。Yang Y[3]基于FAST开发并验证了一种地震耦合分析和结构控制程序SCASCA，研究了10 MW单桩式风力机在风波-地震耦合下的结构响应。Dai Kaoshan[4]研究了考虑土-构耦合效应（SSI）时调谐质量阻尼器（TMD）对重力式风力机塔架所受地震载荷的影响。闫阳天[5]通过Winkler土-构耦合模型研究了桁架式及单桩式5 MW风力机在正常运行和停机两种工况下的地震动力响应。席仁强[6]采用气动-伺服-水动-弹性耦合方法，通过Seismic程序研究了海上风力机在停机、运行和紧急停机3种工况下的地震动力响应。刘中胜[7]以NREL 5 MW风力机为研究对象，通过Wolf方法建立土-构耦合模型对地震作用下的风力机塔架进行结构控制。邹锦华[8]以50 kW，1.5 MW和5 MW 3种不同容量风力机为研究对象，基于开源软件FAST，通过自编程建立风-地震耦合仿真模型，研究了不同强度地震和湍流风联合作用下的风力机动力学响应。

已有研究以5 MW和10 MW风力机为主，出于经济因素考虑，海上风力发电为了降低运营成本，必须增大风力机功率，提高单机容量，因此，15 MW超大容量风力机将成为未来风电发展的主要方向之一。文献[9，10]研究了风-浪-地震联合作用效应以及土-构耦合效应对15 MW海上风力机地震动力响应的影响特性，结果表明，地震显著增强了15 MW风力机的塔顶振动和塔基载荷，需要对其进行抗震控制，以降低结构振动幅度和载荷。

本文通过对开源软件FAST进行二次开发，基于TMD控制方法，建立了地震条件下通用的海上风力机动力学分析及控制模型，以IEA 15 MW单桩式风力机为研究对象，研究了TMD控制参数对不同地震作用下的风力机减载抑振效果。

1 IEA 1 5 MW风力机模型

在国际能源署的资助下，美国可再生能源实验室与丹麦科技大学联合设计了一台专门用于海上风电研究的15 MW单桩风力机，即IEA 15 MW风力机[11]（图1）。

图1 IEA 15 MW单桩式海上风力机Fig.1 The IEA 15 MW monopile offshore wind turbine

IEA 15 MW风力机的单桩直径为10 m，叶片长度为117 m，是目前公开用于学术研究的最大尺寸的风力机。其额定风速和转速分别为10.59 m/s和7.56 r/min，对应的设计尖速比为9，最大叶尖速度为95 m/s。其主要设计参数如表1所示。

表1 IEA 15 MW风力机主要设计参数Table 1 Main parameters of the IEA 15 MW wind turbine

2 研究方法

2.1 地震载荷计算方法

为了解决大质量法的局限性，本文通过修改FAST中风力机动力学方程，实现了土木工程中广泛应用的通用模态加速度地震载荷计算方法，从而考虑地震载荷与其他环境载荷的联合作用，分析流程如图2所示。

图2 风力机地震动力学分析流程图Fig.2 Flowchart of seismic analysis of wind turbines under earthquake loadings

在FAST中，单桩基础和塔架被视为一个整体支撑结构，采用线性模态法对其进行结构动力学建模。在风-浪-震联合作用下第i阶模态自由度的动力方程为

式中：qi，q˙i，q¨i分别为第i阶模态的模态位移、速度和加速度；ωi，ξi分别为第i阶模态的角频率和阻尼比；aeq为输入地震加速度；Faero.i，Fhydro.i分别为第i阶模态对应的广义气动力和水动力；mi为与第i阶模态相关的模态质量；γi为与第i阶模态相关的地震参与系数。

式中：H为支撑结构的长度；ρ（h）为支撑结构的质量密度；φi（h）为支撑结构第i阶归一化模态振型。

在地震荷载计算中，风轮和机舱被简化为支撑结构顶端质量mRNA，其相应的地震荷载Feq.RNA为

2.2 TMD控制方法

为了减缓海上风力机在地震荷载作用下的动态响应，本文基于TMD方法开发了被动结构控制模块。TMD的基本思想是通过在适当位置放置的阻尼器来吸收外部激励能量。本文将两个独立的TMD放置在塔顶，以减轻由于地震荷载引起的支撑结构的纵向和侧向运动响应。

通过修改FAST中的风力机运动学和动力学计算部分的源代码，实现多荷载作用下的TMD控制。将TMD运动产生的力加入到广义力中，即式（1）中的右边项。每个方向上的TMD力（FTMD）推导如下：

式中：xTMD，x˙TMD分别为TMD的位移和速度；kT，cT分别为TMD的刚度和阻尼。

TMD运动受到机舱运动的影响，其加速度x¨TMD可表示为

式中：mT为TMD的质量；x¨N为机舱加速度；ωN，αN分别为机舱的角速度和周向角速度；ωN×xTMD为离心力项；αN×xTMD为欧拉力项；2ωN×x˙TMD为科氏力项。

3 仿真工况

3.1 地震动

本文共选取了5种不同的地震工况[12]，表2给出了这些地震发生的时间、地点和震级等信息，图3为El Centro地震加速度。

表2 地震记录Table 2 Earthquake records

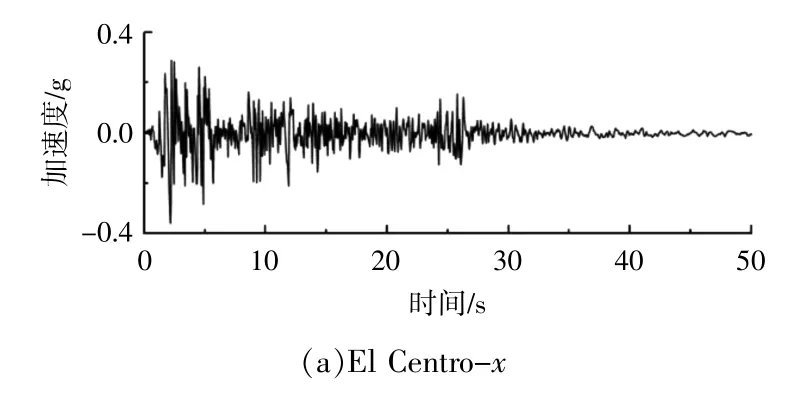
图3 El Centro地震加速度Fig.3 The acceleration of the El Centro earthquake event

3.2 TMD控制参数及仿真设置

本文选取质量比为3%，阻尼比为10%的TMD置于塔顶，针对表2中的5种地震工况，分别计算了调谐频率比为0.80，0.85，0.90，0.95和1.00 5种情况下的塔顶振动和塔基载荷，并与无TMD控制时的结果进行比较，从而分析TMD的控制效果。共30个算例，每个算例仿真时长为300 s，时间步长为0.005 s，在第100秒时加入地震激励。

4 结果分析

4.1 塔顶位移

在停机工况下，地震载荷是塔顶振动的主要激励，塔顶位移（尤其是侧向位移）主要受地震载荷影响[13]。图4为IEA 15 MW风力机在Chi-Chi与El Centro两种地震作用下的塔顶位移时域变化。

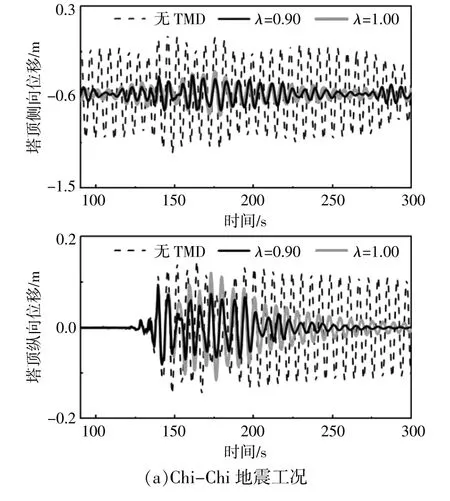
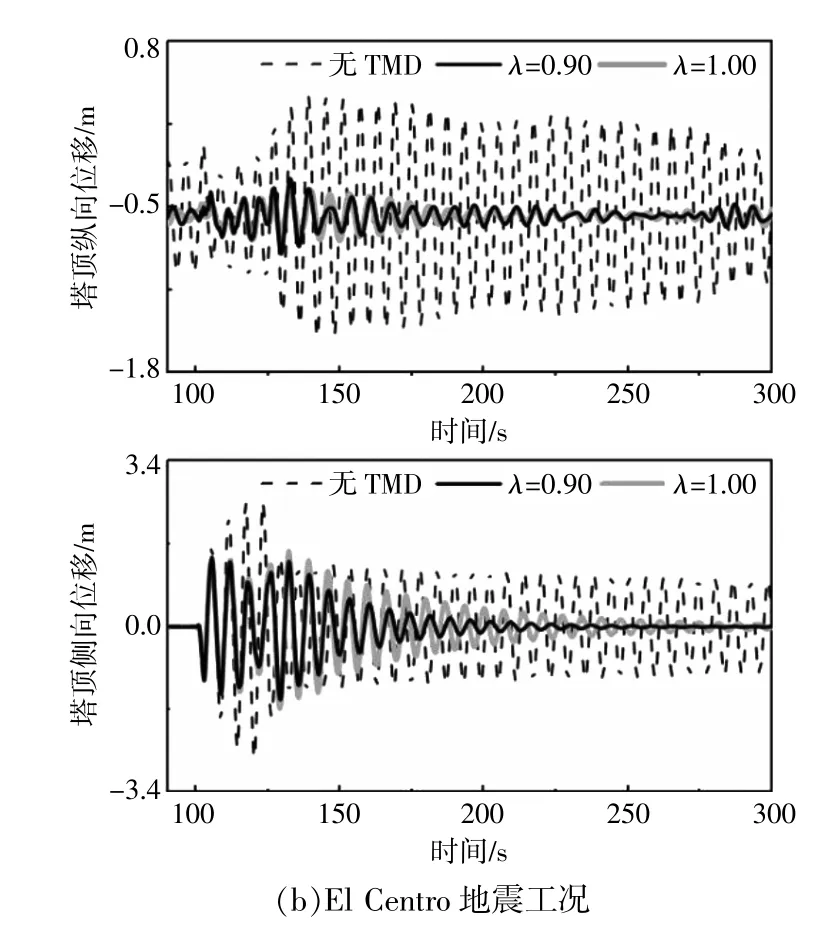
图4 塔顶位移时域响应Fig.4 Variation of tower-top displacement in time domain

由图4可知：地震发生后，无TMD控制时，塔顶位移（特别是侧向位移）急剧增大，在地震结束后（＞150 s），塔顶位移无明显降低的趋势；采用TMD控制后，阻尼器运动有效地降低了塔顶振动幅度，风力机塔顶侧向位移曲线开始趋于0，风力机纵向位移趋于-0.6 m，这主要是由于风轮重心偏离于塔架中心线，从而造成了一定程度的自然弯曲；相比于调谐频率比为0.90时的结果，当调谐频率比为1.00时，塔顶振幅明显更大，这主要是因为加上TMD后，整个系统的质量增大，造成风力机一阶频率降低，因此低频率比的TMD控制效果更佳。

通过对图4结果进行快速傅里叶变换，得到了塔顶位移频域响应（图5）。

图5 塔顶位移频域响应Fig.5 Variation of tower top displacements in frequency domain

由图5可知，加入TMD后，塔架纵向及侧向一阶固有频率（0.16 Hz）处峰值均显著降低，且调谐频率比为0.90时峰值更低，说明TMD在减弱塔顶振动方面具有显著效果。较之于无TMD控制的工况，响应峰值对应的频率均有所降低。

由于地震属于高频激励，不同地震具有不同频域特性。为了避免地震随机性导致的偏差，本文计算了表2中5组地震作用时不同调谐频率比及TMD控制下的塔顶位移峰值及其降低比例，结果如图6所示。

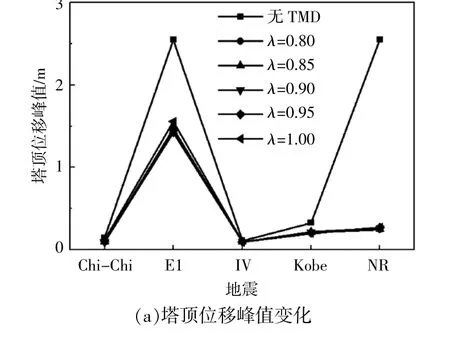
图6 塔顶位移峰值及TMD减振比例Fig.6 Peak displacement of tower-top and the corresponding mitigation percentage

由图6（a）可知：不同地震作用下，塔顶位移峰值不同，Chi-Chi和IV（Imperial Valley）地震的地面加速度峰值相对较小，所以塔顶位移峰值均较小；TMD可以显著降低El（El Centro）和NR（Northridge）地震作用下的塔顶位移。

由图6（b）可知：在EI和NR地震工况下，使用TMD可以分别降低塔顶位移峰值40%和80%以上，说明TMD对风力机减振控制具有十分明显的效果；除Chi-Chi地震之外，采用不同调谐频率比的TMD控制效果较为接近，其中调谐频率比为0.90的TMD在所有地震工况下均具有较好的控制效果，降低塔顶峰值比例均高于30%，其在NR地震工况下的减振比例可达89.8%。

4.2 塔基载荷

图7为Chi-Chi和El Centro地震工况下塔基弯矩的时序变化曲线。

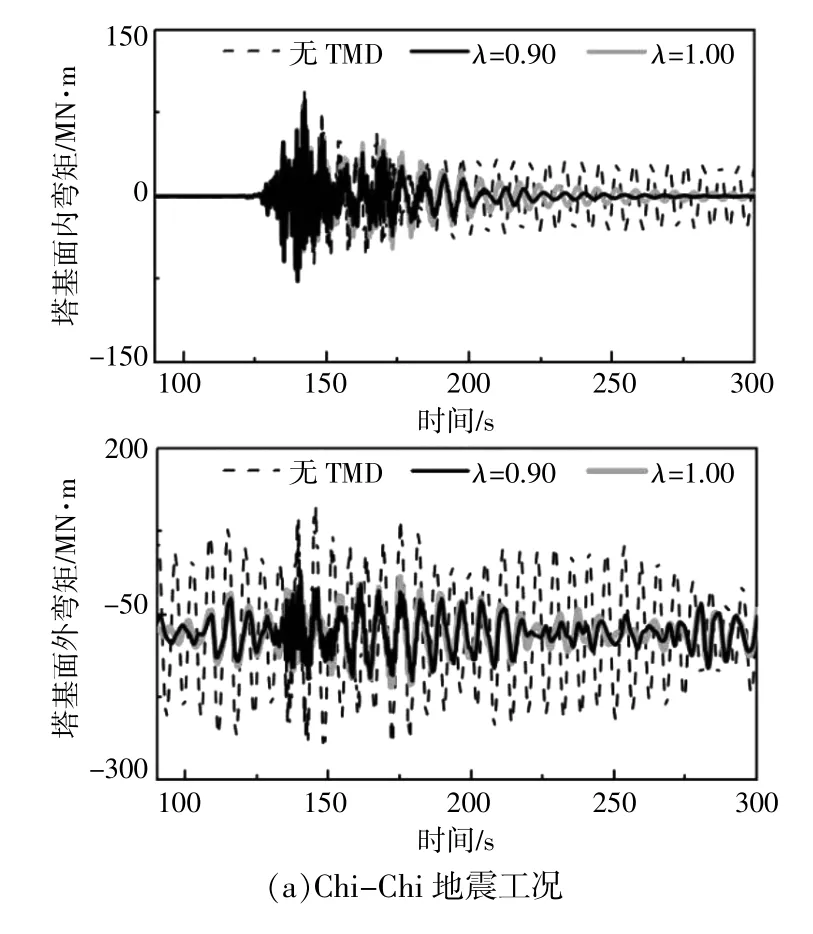
图7 塔基面内及面外弯矩时域响应Fig.7 Variation of tower bending moment in time domain

由图7可知：在地震发生后，塔基面内弯矩急剧增大，但地震对面外弯矩的影响相对较小；TMD对塔基弯矩峰值的影响相对较小；在无TMD控制时，Chi-Chi地震工况下的塔基面内弯矩峰值为97.5 MN・m，而当调谐频率比为0.90和1.00时，该值分别为86.7 MN・m和85.1 MN・m，分别降低了11.1%和12.7%。无TMD控制时，El Centro地震工况下的面内弯矩峰值为1 473 MN・m，加入调谐频率比为0.90和1.00的TMD控制后，塔基弯矩峰值略有降低，分别为1 084 MN・m和1 077 MN・m，降低幅度低于30%。虽然TMD无法显著降低塔基弯矩峰值，但可以显著降低地震后的塔基载荷。以Chi-Chi地震结果为例，加入调谐频率比为0.90的TMD控制后，在150～300 s期间的面内弯矩标准差从22.6 MN・m降低为8.6 MN・m，面外弯矩标准差由81.3 MN・m降低为25.7 MN・m，降低幅度超过60%。

通过对图7中的时域结果进行快速傅里叶变换，可以得到塔基弯矩频域响应（图8）。

图8 塔基弯矩频域响应Fig.8 Variation of tower bending moment in frequency domain

由图8可知：TMD显著降低了塔架一阶固有频率（0.16 Hz）处的响应幅值，以Chi-Chi地震为例，当TMD调谐频率比为0.90时，一阶固有频率处的面内弯矩幅值从15.2 MN・m降低为3.8 MN・m，降低幅度达75%；对面外弯矩的影响更大，一阶固有频率幅值降低了80%。由于单个TMD只能降低地震对结构一阶模态的影响，对塔架二阶模态（1.4 Hz）处的响应没有任何影响。

图9为150～300 s塔基载荷（面内弯矩）标准差降低比例。

图9 TMD降载比例Fig.9 Reduced load ratio of TMD

由图9可知：除Chi-Chi和El（El Centro）地震外，在其他3种地震工况下，当调谐频率比不同时，TMD对塔基载荷降低幅度影响不大；在Chi-Chi和El地震作用下，TMD降载比例随调谐频率比的增大而减小，呈现出一定的线性关系；相比于调谐频率比为0.9的TMD，调谐频率比为0.8的TMD具有更好的降载效果，在5种地震工况下的降载幅度分别为70.6%，92.2%，86.1%，67.7%和99.0%。

5 结论

本文通过对开源软件FAST进行二次开发，建立了海上风力机地震动力学仿真及控制程序。研究了不同控制频率的TMD对IEA 15 MW单桩风力机在多种自然地震作用下的塔顶振动和塔基弯矩的影响。结果表明，TMD可以有效降低塔顶振动，调谐频率比为0.90的TMD可降低塔顶侧向位移峰值达89.8%。同时，TMD也可有效降低塔基弯矩，特别是地震结束后的弯矩波动幅度，采用调谐频率比为0.80的TMD时，面内弯矩的标准差最高可降低92.2%，且塔架一阶固有频率处的弯矩幅值显著降低，最高降低比例可达84.8%。