考虑通信延时的可再生能源与火力发电耦合系统无功控制优化
孙峰,赵清松,,王若瑾,戈阳阳,王晓东
(1.国网辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006;2.沈阳工业大学 电气工程学院,辽宁沈阳 110870)
0 引言
随着“双碳”目标的提出,可再生能源发电场站与火电机组之间的电气联系日益紧密[1],但由于缺少整体协调控制,可再生能源与火电厂的整体利用率较低。将可再生能源发电场站与火电厂集成多能源耦合系统进行统一控制优化,可提高电力系统在远端故障、电压扰动中的抵御及快速恢复能力。但在耦合系统实际运行中,由于通信设备之间距离、带宽、协议转换等原因,通信延时不可避免且差异较大,影响无功控制对电压控制的效果[2]。因此,将电力系统中的无功补偿和可再生能源的无功调节相结合,具有重要意义。
电力系统的无功补偿通常运用各种补偿设备进行调压,如电容器、调相机和SVG对接入点进行无功控制[3]。文献[4]中的电容器、电抗器组根据集成控制系统的命令,维持电压和功率因数。但它们无法满足响应速度的要求。静态无功补偿器(Static Var Compensator,SVC)可以实时调节无功功率,被广泛用于风电场的无功补偿[5]。但SVC价格昂贵,且SVC易出现明显的响应延时、电压过冲和风机级联跳闸现象,因此SVC无功调节容量有限。单独使用SVC难以满足恶劣环境下大型风电场的无功补偿需求[6,7]。作为紧急情况下的辅助控制,需要挖掘和利用风力发电机组的可用容量来支持电网电压。上述无功补偿方式所需成本高,对于耦合系统并非较优方案。文献[8]分析了基于电容器无功补偿的风电场并网协调控制策略,但所提方法不适用于可再生能源与火电的耦合系统。文献[9]分析了光伏无功出力和SVG结合的协调控制策略,但所提方法没有考虑通信延时对电力系统带来的影响。文献[10]分析了风光储直流微电网建模与仿真,但所用模型不适合可再生能源与火电厂耦合系统模型。现有方法主要通过电容器、SVC和SVG等电力电子设备对新能源系统进行调节,较少有直接通过风电场对电力系统进行无功控制,并且较少考虑通信延时对风电场无功控制的影响。
本文主要针对风、光、火耦合系统的无功控制优化问题,在保障火电厂和光伏电站输出最大功率的前提下,通过SVG无功补偿和风电机组无功控制的方法提高了耦合系统的电压稳定性。在分析可再生能源电站与火电厂耦合系统架构、风电机组无功调节潜力和控制策略的基础上,分析了通信延时对耦合系统电压稳定性的影响,以电压偏差和网损最小为目标,利用Ybus与线性递减权重粒子群(Linearly-decreasing Weight Particle Swarm Optimization,LinWPSO)算法使全网电压水平总体最优,得到全网最佳电压分布。
1 耦合系统结构及其无功控制特性
1.1 耦合系统及其结构
可再生能源与火力发电耦合系统中,各电源无功输出直接影响系统电压稳定性。通过改变系统中无功潮流,可降低各节点的电压波动和网损,提高系统安全稳定性。无功容量优化配置主要是协调各发电单元,使得耦合系统的各个发电单元高效配合,为了给用户提供更加可靠的电能,需要选取合理的无功配置进行无功优化控制,保障有功功率高效快速地传输和耦合系统稳定地运行。耦合系统主要是分布式电源通过交流母线的耦合技术,将风力发电、光伏发电和火力发电接入到系统中,最终整个系统只能通过配电柜连接到大电网。各节点通过母线耦合器连接,使得各个节点之间实现了电气隔离,各个发电源可以相对独立运行,使各发电源最大程度实现解耦,提高了耦合系统的稳定性[11,12]。为了分析无功优化配置对电压稳定性的影响,本文建立了可再生能源与火力发电耦合系统模型。可再生能源与火力发电耦合系统拓扑结构如图1所示。

图1 可再生能源与火电耦合系统拓扑结构Fig.1 System diagram of coupling of renewable energy and thermal power
图中包括1个火电厂、1个光伏电站、2个SVG、3个双馈风电场和若干用户,上述设备通过变压器与电网连接(节点0)。
1.2 耦合系统中的风电场无功控制
早期的风电场并网多利用电容器、SVC和SVG等无功调节设备,增加了投资费用且降低了风电场的利用率。针对该问题,可选用SVG和风电场作为无功调节源,利用其本身的无功调节潜力替代传统无功补偿装置,减少投资成本。SVG和风电场无功调节主要根据测量点电压偏差,调节装置的功率因数以及控制电压从而控制机组的无功功率变化。SVG功率因数控制主要通过无功补偿调节系统功率因数,功率因数调节可以提高耦合系统整体利用率,但在无功调节上缺少灵活性。风电场电压控制是利用风电机组的无功功率稳定机端电压。为了降低投资水平和充分发挥风电机组的无功调节潜力,本文制定了电压偏差和网络损耗权重结合后的总目标函数,首先利用SVG优化控制,再利用风电机组进行优化控制。
本文采用SVG和风电机组双层控制的方式,具体步骤如下:①采集耦合系统各个节点数据(电流、电压、有功功率、无功功率、系统的阻抗)和风电场出口侧数据(有功无功出力、接入节点、接入电压等级等);②通过潮流计算获取各节点的电压偏差;③将耦合系统节点电压偏差最严重的3个节点作为接入节点,通过依次采用风电场功率因数控制和电压控制的无功控制方式对耦合系统进行控制。
1.2.1风电场无功控制方式与特性
当风电场接入多个耦合系统节点时,节点i(i=1,2,…,N)处风电机组出力为PWi+jQWi;当无风电机组接入节点i时,存在PWi=0,QWi=0,对应节点i与i-1之间的电压损失为
节点i的电压为
式中:U0为线路始端(节点0)的电压幅值;PLj,QLj分别为节点j处耦合系统线路上的有功功率和无功功率;PWj,QWj分别为风电机组在节点j处释放的有功功率和无功功率。
耦合系统经过风电机组功率因数控制后,再基于风电场并网点电压调节无功功率,从而提高耦合系统电压的稳定性。耦合系统中风电场的电压控制原理如图2所示。
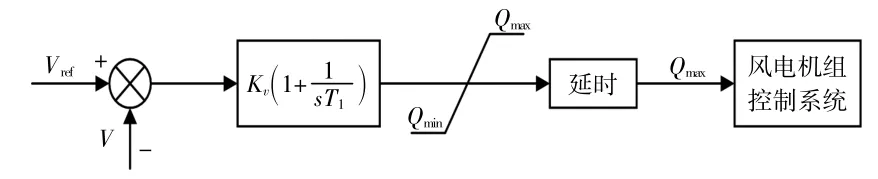
图2 风电场电压控制结构图Fig.2 Wind farm voltage control structure diagram
图中:Kv为风电场的电压无功PI控制器设定的比例系数;T1为时间积分常数;Qmax,Qmin分别为风电场的最大和最小无功功率。
通过PI控制器得到电压的指令值Vref和反馈值V,根据Vref和V的差值计算无功功率。同理,PI控制器的输出结果先后经过限幅环节和时间延时模块,进而获得无功功率的参考值,然后输入风电场的下一级控制系统,最后在变流器的控制下输出无功功率。
1.2.2通信延时对耦合系统无功控制的影响
在耦合系统中,可再生能源分布范围广,控制信号通过长传输线进行传输,通信延时难以避免。通信延时对基于耦合系统的风机i的附加无功控制系统如图3所示。Hi(s)包括放大和滤波等链接。

图3 通信延时对风电场无功控制的影响Fig.3 The influence of communication delay on reactive power control of wind farm
当风力发电机组i的通信延时的时间为τi时,延时的影响主要体现在s域反馈信道中引入了延时链路e-τi。延时的表达式是反馈信号的频移,频移与延时的时间τi成正比。频率偏移表现为信号功率谱密度的变化。由于风电机组控制系统之间的区域差异,导致各种延时的产生,进而引起信号功率谱密度的变化,控制信号经过长距离处理和传输后,会产生多余的频率分量,该分量会降低电网的电压质量,并且影响公共母线电压。
为了保证耦合系统的无功功率控制达到预期调节效果,必须重视通信时延的影响,并考虑降低时延的有效手段。为了分析通信延时对耦合系统电压的影响,以耦合系统母线电压A相的电压波动为例,在通信延时时间为10,20 ms条件下,对耦合系统模型进行了仿真。图4为有、无风电场控制下的通信延时对耦合系统母线电压的影响。
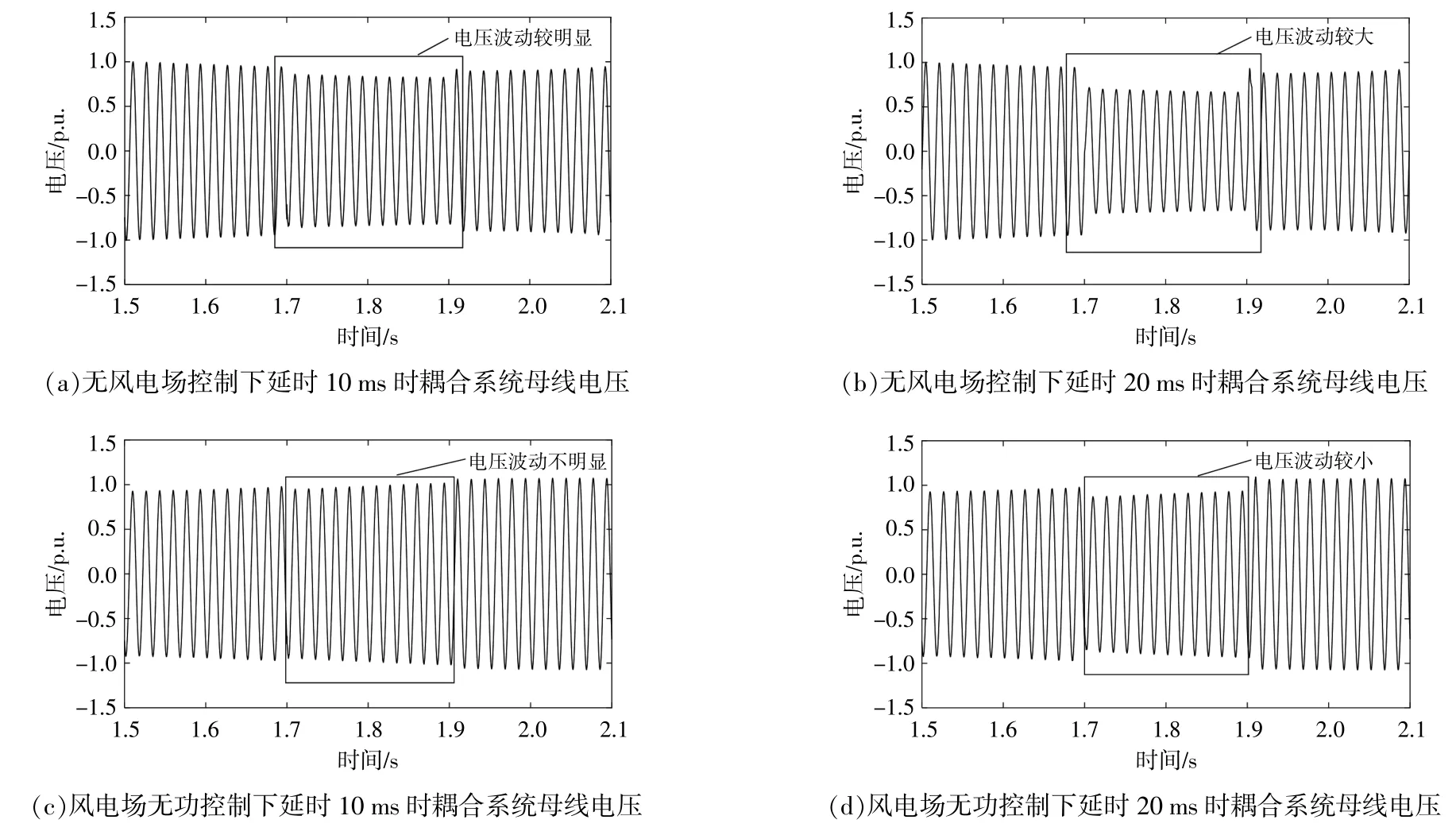
图4 有无风电场无功控制的通信延时对耦合系统母线电压的影响Fig.4 The influence of communication delay under the reactive power control of no wind farm on the bus voltage of the coupling system
由图4可以看出:①通信延时的增加使得母线电压波动幅度变大。当耦合系统通信延时时间为10 ms时,母线电压波动较小,电压幅值波动在±0.87 p.u.,电压下降约13%。当延时时间为20 ms时,电压幅值波动在±0.72 p.u.,电压下降约28%。由于耦合系统无功调节设备不能提供充足的无功补偿,导致故障期间母线电压幅值下降较大,电压存在明显的波动,但其他任意时刻的电压幅值不再保持不变。相对于10 ms的延时时间,20 ms时电压信号变化更明显,使电压在无通信故障时也发生少许偏移;②为了减少延时对耦合系统稳定性的影响,通过SVG无功补偿和风电场电压控制的方式对耦合系统进行无功补偿。该无功控制能够提供充足的无功,在延时时间为10 ms时,电压幅值波动在±0.97 p.u.,电压下降约3%,它的效果几乎没有延时。当延时时间增加到20 ms时,电压幅值波动在±0.95 p.u.,电压下降约5%,电压波动程度明显降低。
因此,基于风电场无功控制下的母线电压效果优于无风电场控制的效果。验证了基于SVG无功补偿和风电场电压控制方式能够保障系统电压的稳定性。
2 可再生能源与火力发电耦合系统双层无功控制优化策略
2.1 耦合系统双层无功优化框架
耦合系统的电压合格是电力系统的重要考核指标,电压波动会影响电力系统的稳定和用电设备的使用。本文提出一种以电压(0.95~1.05 p.u.)合格为约束[13,14],分别在系统层、机组层利用SVG和风电机组对耦合系统进行无功优化调压。首先,通过SVG对耦合系统进行无功补偿,确定耦合系统最优功率因数;其次,以节点电压偏差和网损权重结合后的函数为总目标,利用风电机组的无功输出,确保耦合系统各个节点的电压幅值在正常范围内。SVG和风电机组多点接入双层调控策略流程如图5所示。

图5 耦合系统双层调控优化策略流程图Fig.5 Flow chart of two-layer control optimization strategy of coupled system
以各节点电压值偏差为依据,通过SVG对系统整体进行无功补偿,确定系统最优功率因数。对于电压偏差严重的节点,以电压偏差和网损最小为目标,计算δ1和δ2的最优权重组合,得到临近风电场的风电机组最优输出无功功率,使得各节点电压保持在稳定状态。通过SVG和风电机组无功优化双层结构,最终实现了耦合系统各节点电压稳定和网损最小。
2.2 风电机组无功优化模型
耦合系统接入风电场后,由于风电场出力的随机性和波动性会影响风电场的无功功率的稳定,使得耦合系统对风电场的无功调节提出了更高的要求。本文以电压偏差和网损为目标,以有功功率和无功功率为优化变量,求解耦合系统最优功率因数,通过SVG无功补偿调节耦合系统功率因数,以风电场电压控制的方式调节系统电压稳定,利用Ybus-LinWPSO算法对无功优化模型进行求解。
2.2.1目标函数
电压偏差是衡量电力系统稳定运行的重要指标,过大的电压偏差会缩短电力设备的寿命,降低供电的可靠性,还会对系统的无功补偿产生不利影响。因此,在风电场接入并网调控时,本文以电压偏差率最小F1为目标函数,即:
式中:UN为节点电压额定值。
风电场接入点并网时,需要考虑风电场对接入点电压偏差的影响,同时还需要考虑对母线其余节点影响的协调运行问题。在兼顾电压偏差的影响下,为保障耦合系统的经济效益,以电网系统的总网络损耗最小F2为目标函数,即:
式中:Gij,Bij为组成矩阵的元素;Ui和Uj分别为节点i和j的电压幅值;θij为相角差。
通过分析节点电压偏差和网络损耗两个子目标在总目标函数中的影响度来确定权重的大小,目标函数为
式中:δ1,δ2为权重系数。
2.2.2约束条件
目标函数的约束条件是为了满足电网的安全稳定运行,等式约束的目的是为了保障耦合系统功率的平衡性,不等式约束设定根据需求的不同而变化。
风电场并网后的潮流等式约束条件为
式中:Bij,Gij分别为节点i和j的电纳和导纳;δij为功率角;PGi,QGi,PWi和QWi分别为耦合系统接入节点i和接入的风电场i的有功、无功功率。风电场输出功率的不等式约束条件为
风电场对应的节点电压和无功补偿量为

支路电流的不等式约束为
3 无功优化模型求解方法
为求解耦合系统无功控制优化模型,本文提出了一种Ybus-LinWPSO方法用来求解系统最优功率因数和最优机端电压值。由于求解耦合系统各节点的有功、无功功率和电压偏差计算量较大,需要引入一种快速求解的潮流计算方法。Ybus高斯迭代潮流计算方法具有收敛可靠、计算速度快且对初值要求低的优点[15]。LinWPSO算法的全局搜索能力较强、收敛速度快,且求解精度高,选用Ybus-LinWPSO算法可在快速潮流计算的基础上提高求解精度。因此,本文采用Ybus-LinWPSO算法求解优化模型,步骤如下。
①设置LinWPSO算法参数,随机产生风电场有功出力值PW、无功出力值QW、接入节点i数量。
②输入时段t时电网侧的输入有功、无功功率实数值PLit和QLit。
③将风电场随机产生的PW和QW作为输入变量,得到各个节点电压区间中值Uit,以节点电压Uit与额定电压U0的偏差最小为目标,找出全局最优解。
④更新节点电压Uit、有功出力值PW和无功出力值QW的速度和位置,更新并重新进行Ybus潮流计算,得到适应度值后继续更新种群位置和速度进行计算。
⑤在(0,1)内以步长0.001分别计算每个δ1对应的总电压偏差,将最小电压偏差对应δ1的值确定为最优值,最终得到的δ1和δ2为最优权重组合。
⑥达到最大迭代次数后,输出最优变量值。
4 算例分析
本文可再生能源与火电耦合的系统模型结构如图1。其中:电压等级为35 kV,1节点接入火电机组,考虑到本文模型以可再生能源高比例系统为前提,为满足系统整体协调性,将火电机组缩小为100 MW接入到耦合系统中;在17节点接入光伏电源,3,16节点和25节点分别接入风力发电机组。优化问题采用Ybus-LinWPSO模型求解方法,求解参数和耦合系统模型参数设置如表1和表2所示。

表1 Ybus-LinWPSO算法参数设置Table 1 Ybus-LinWPSO algorithm parameter settings
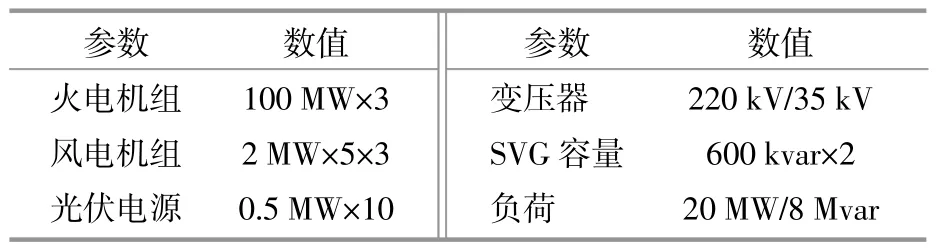
表2 耦合系统模型参数设置Table 2 Coupling system model parameter settings
以辽宁某地区天气为例,按照当地气候特征将全年分为夏季和冬季,测得所在地气象数据,模拟某日逐时单位容量风电机组发电功率,并采用基于正态分布的典型日拟合方法分别拟合夏季典型日与冬季典型日的全天单位容量的风电逐时发电功率曲线[16],如图6所示。
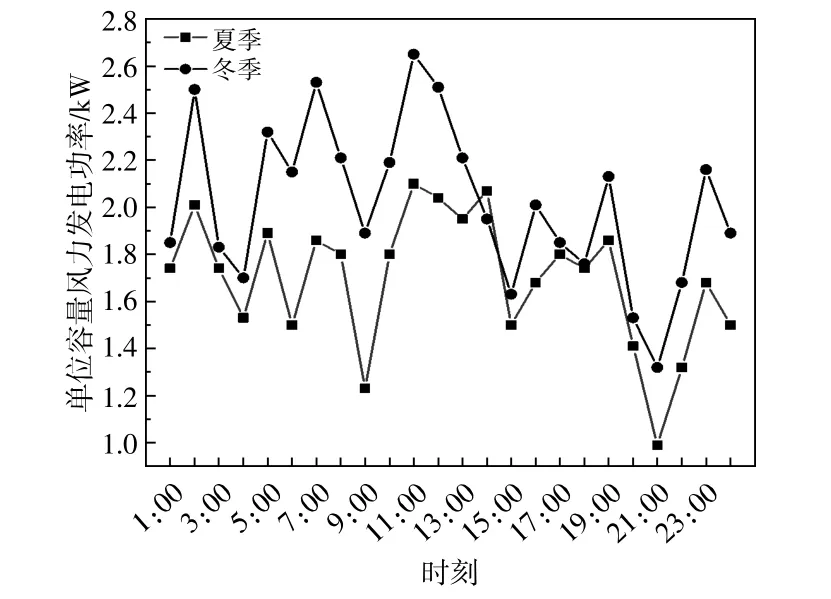
图6 典型日风机逐时发电功率Fig.6 Typical daily wind turbine hourly power generation
由图6可得:夏季风机整体发电功率波动相对较小,冬季风机整体发电功率波动相对较大;在13:00-14:00,风机输出功率相对较小。因此,需要通过增加风电机组的无功功率来保障该时间段的电压稳定。
4.1 功率因数控制结果分析
本文选取15和21节点作为SVG的接入点,接入SVG后,在20 ms通信延时影响下,对不同功率因数下的各节点电压进行仿真,通过测量模型各个节点的电压值,得到4种功率因数下的电压分布,如图7所示。

图7 不同功率下的可再生能源与火电耦合系统的电压分布图Fig.7 The voltage distribution diagram of the coupling system of renewable energy and thermal power under different power
由图7可知,功率因数会对节点的电压造成影响。当功率因数由-0.85逐渐向-0.95调节时,对应的节点电压逐渐升高,例如:当功率因数为-0.95时,对应的16节点的电压依然维持在1 p.u.附近;当功率因数为0.85时,对应的16节点的电压可降低接近0.9 p.u.。由此可知,本文策略能够合理地调节功率函数,可以得到更加优化的电压分布,也会缩小对应的节点电压偏差。因此,本文选取-0.95作为系统的功率因数并继续对风电场进行电压控制。
4.2 无功优化结果分析
为保证耦合系统的电压稳定性,在选取-0.95作为功率因数之后,进一步对风电场进行电压控制。由于不同时段的可再生能源的有功输出不稳定,且风电、光伏和火电耦合系统不协调,导致接入节点电压越限,无功调压有效利用率降低。因此,通过风电场对耦合系统进行无功补偿。
本文以辽宁某地区情况为例,通过监测该地区的日发电功率,选取电压越限严重的11:00-14:00时间段作为重点研究对象,通过增加风电场的无功功率对耦合系统进行电压优化控制。图8为风电场无功优化结果的对比。图9为24 h内风电场输出的无功功率。

图8 11:00-14:00无功优化前后电压区间对比Fig.8 Comparison chart of voltage interval before and after reactive power optimization during 11:00-14:00 period

图9 风电机组24 h输出无功Fig.9 Wind turbines output reactive power 24 hours a day
由图8可知,11:00-14:00的电压越限严重,经过无功补偿后,该时段电压幅值全部落在[1.01,1.05]内。由图9可以看出,11:00-14:00的风电机组无功输出较大。优化结果说明风电场无功控制可以提高系统电压水平,保障各节点电压稳定性。因此,本文所提的风电场无功优化控制方法在通信延时下可以改善耦合系统的电压越限问题,提高耦合系统电压稳定性。单位容量的SVG成本为25万元/Mvar[17,18],根据图9可知,单台风电机组可释放的无功容量最大约为0.85 Mvar,本文风电机组共可提供无功容量为12.75 Mvar。若使用SVG替代,则需13 Mvar,增加325万元成本。风电机组损失的电量成本远小于SVG无功补偿成本。因此,充分利用风电机组无功补偿,可降低一定的经济成本。
将LinWPSO算法与粒子群算法(PSO)、蚁群算法(ACO)进行对比,结果如图10所示。

图10 不同类型的优化算法对比图Fig.10 Different types of optimization algorithm comparison chart
5 结论
本文针对可再生能源与火电系统耦合系统电压稳定性问题,提出了一种考虑通信延时的SVG和风电机组双层无功控制优化策略,上层采用SVG无功调节,选出系统稳定性最好的最优功率因数,下层采用风电机组无功调节,通过Ybus-LinWPSO算法求解出风电机组最优无功参考值。通过所搭建的可再生能源与火力发电耦合系统仿真模型进行仿真实验,结果表明:①采用SVG功率因数调节可以有效抑制整个系统的节点电压越限,在功率因数调节的基础上进一步进行风电场电压控制,减少了耦合系统电压越限的节点数;②采用Ybus-LinWPSO算法对无功优化模型分步实施优化策略,可以加快收敛速度,得到更优的无功配置结果;③通信延时的增加会导致母线电压波动增大,风电场无功控制可以减少通信延时对耦合系统带来的影响。
本文所提风电场无功优化方法考虑了通信延时对耦合系统带来的影响,有效抑制了可再生能源出力波动和远端扰动给耦合系统带来的电压扰动,提高了耦合系统电压的稳定性,同时对新能源与火电机组的耦合发展具有重要意义。

