考虑相关性与平滑效应的海上风电场集群汇集系统拓扑优化

谢珍建，许偲轩，李辰，李海波，江坷滕，鲁宗相

（1.国网江苏省电力有限公司经济技术研究院，江苏南京 610095；2.清华四川能源互联网研究院，四川成都610000）

0 引言

与内陆风力资源相比，海上风力资源更加稳定，风能质量更好，发电效率更高，对人类生活的直接影响较小[1-3]。风电汇集系统承担着汇集风机电能并向内陆电网输送的任务。在海上风电汇集系统规划过程中需保证风电发电效率和可靠性需求，因此海上风电场从环境和技术的角度相较于其他发电方式具有更昂贵的建造、运维费用，其电网接入成本也是重要的经济成本之一。

海上风电场集电系统拓扑优化是对风机机组、汇集站和集群中心站的空间位置和连接方式进行优化[4，5]。一些学者首先从不改变现有拓扑的角度出发，针对“弃风”问题设计新设备来提高系统可靠性。文献[6]提出了直流集电器的概念，设计了一个集汇集升压、控制保护、故障隔离的综合性平台取代传统的分布式升压站。文献[7]设计了一种分流电路来保证风机在最大功率追踪条件下的输出电压稳定，降低了风机间的耦合性和脱机率。另一种优化方向为集电系统的拓扑结构多层设计优化。已有的优化方案有变风机选址和变集电平台选址的双层优化[8-11]和子区域风电汇集站选址和中心汇集站选址的双层优化[4]等。针对拓扑结构的优化，文献[8-14]提出了改进遗传算法、模糊化算法、混合生态共生算法、拓扑连线优化算法和基于改进最小生成树的经典Prim算法。这些算法均以实现综合经济效益为目标，给出了最终的拓扑结构。文献[8-10]将风机划分为集群子区域，多个区域之间采用星型结构连接。文献[11-14]尽管给出了可靠性和可行性分析，但由于没有考虑集群海上风电场出力之间的互补性与相关性，其规划结果有进一步优化的空间。

现有的研究更侧重从拓扑结构的经济性、可靠性等角度开展优化研究，但是并未考虑海上风电出力特性与平滑效应[15，16]。根据实际风电场数据可知，海上风电场出力利用小时数较高，且具有较强的相关性和空间平滑效应。相关性大导致风电场集群出力仍有较强的波动性，空间平滑效应则削弱了波动性，使集群出力表现出更加稳定的特征。实际工程中，若不考虑海上风电场集群出力特性对汇集和输送系统容量的影响，则会导致规划容量过大，经济性较差。因此在汇集系统优化中，应结合风电场出力时序数据，通过容量优化合理平衡弃风电量与经济性。

本文提出了一种考虑相关性与平滑效应的海上风电场集群汇集系统拓扑优化方法。首先基于我国某沿海省份风电场实际历史出力数据，开展相关性与平滑效应分析，进一步考虑系统投资成本、运行成本与弃风成本等，以净收益最大为目标，建立了风电场集群汇集系统优化规划模型。采用改进遗传算法对风电场内部风机拓扑结构和风电场汇集拓扑进行了优化分析，并以沿海某风电场集群作为对象，验证了本文所提出方法的有效性与正确性。

1 海上风电汇集系统

本文简要介绍海上风电汇集系统，并结合风电场实际历史出力数据分析其相关性与空间平滑效应。为简化分析，本文做出如下合理假设：①海上风电场的装机容量及其年出力特性已知；②陆上电网足以输送并消纳通过海上风电场群汇集系统注入的功率；③暂不考虑多年滚动规划以及电源、电网规划的时序不匹配问题。

1.1 集电系统拓扑优化模型概述

海上风电汇集系统首先通过输电网将风机发出的电能通过海上升压站统一汇集，再通过线缆传输到陆上电网。江苏某海上风电场群采用树形拓扑，模型如图1所示。

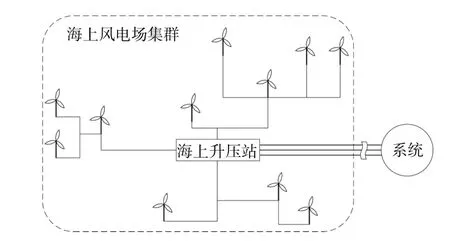
图1 海上风电场集群接入系统示意图Fig.1 Schematic diagram of offshore wind farm cluster access system

由图1可知，风电从各个风电场出发，经过多个风电场汇集后，通过高压输电网络传输至海上升压站。在风电场和海上升压站选址确定的条件下，以风电场全生命周期效益最大为目标，优化风电场分组汇集结构，汇集过程中线路和变电站的技术经济参数是优化结果的重要影响因素。

1.2 海上风电场集群特性分析

在“风电机组-风电场-海上升压站-输电系统-陆上电网”的汇集传递过程中，海上风电的有功输出在空间上具有互补性，通过汇集不同区域的海上风电有利于减少出力波动性，使得风电机群出力特性曲线更加平滑，也称作风电出力的平滑效应或汇聚效应。对江苏某地区的数个海上风电场组成的集群进行历史数据统计，得到风电场集群出力曲线，如图2所示。

图2 江苏某地区风电场集群出力曲线Fig.2 Output curve of wind farm cluster in a certain area of Jiangsu

由图2可以看出，多个风电场出力具有明显的相关性，同时由于空间平滑效应具有一定的互补性，相比单个风电场波动性有所减少，最大出力标幺值降低约为0.85 p.u.，验证了风电场集群的平滑效应。在风电场汇集系统容量优化中，应充分利用风电场集群出力这一特性，对汇集线路的容量进行优化，在满足风电消纳目标的前提下最大化系统经济效益。

本文提出了一种考虑平滑效应海上风电场汇集系统拓扑优化方法，根据海上风电场集群出力特性，建立系统接入协调的规划模型，以经济性最优为目标，依据未送出及送出风电电量的损失及效益、建设成本等因素进行优化分析，对风电场内部的风机拓扑结构进行优化，并对风电场汇集拓扑进行优化，从而完成整个海上风电场汇集系统的拓扑优化。

2 海上风电汇集系统优化建模

2.1 目标函数

对于风电场或风电场集群的送出线路，如按照装机容量进行配置，则会经常导致输电线路轻载，资产利用率低下；如果送出线路容量过低，又会造成大量弃风。因此需要建立经济性综合优化模型，协调输电线路的建设容量与弃风损失。输电线路综合效益的成本及收益为

式中：Btotal为年度收益；CL为年度成本；r为利率；N为运行年限。

风电场送出电能为线路的收益来源，因此传输容量限制造成的弃风，即未送出电量，也应作为罚款计入线路的收益。忽略风电场送出电能不同时段的价格差异，风电场年度收益Btotal由风电收益BTE和弃电补偿成本Ccur组成，其中，BTE主要由风电站年发电量决定，Ccur主要由输电容量限制导致的风电年弃电量决定，计算方法为

式中：BTE为风电电量收益；Ccur为弃电补偿成本；po，pb为价格参数；Ecur为风电场的年弃电量；E为风电场的年发电量。

图3为某海上风电场的年持续出力曲线，即Pdur（t）。

图3 风电场持续出力曲线Fig.3 Continuous output curve of wind farm

当风电场理论出力大于其出口线路有功功率限制PLL时，超过PLL的部分将被弃电。根据上述定义，风电场的年弃电量Ecur和年发电量E分别为

式中：TLL为出力曲线大于PLL的时间；Pdur，max为风电场的年最大出力；E0为风电场年理论可发电量。

根据持续出力曲线，可得：

2.2 约束条件

在对海上风电汇集系统进行优化建模时，应分别对海底线缆的最大负载电流、线缆的最大传输功率、线缆能够挂载的最大风机数设置约束条件，并且考虑海底线缆不允许交叉铺设的问题。

①海缆传输容量约束

海缆所传输的电能不超过海缆的最大传输容量，即：

式中：Sij为与海缆i相连的风机j的电能；ni为与海缆i相连的风机数量；Simax为海缆i的最大传输容量；N为海缆数量。

②海缆载流量约束

海缆载流量约束包括单风机海缆和汇集海缆两部分，其表达式为

式中：Iij为连接风机j的电缆i的载流量；Pwj为风机j的额定出力；Uij为海缆ij的额定电压；cosφj为风机j的功率因数；Ii为连接了ni台风机的电缆i的载流量；Ui为汇集海缆i的额定电压。

③海缆承受风机数量约束

海缆载流量有限，结合式（8）可知，每条海缆能汇集的风机数量ni有限，其表达式为

式中：Imaxi为汇集电缆i的最大载流量；cosφi为汇集海缆i的功率因数；Pw为与汇集海缆i相连的风机的平均额定出力。

④海缆交叉规避约束

在实际工程中，海缆之间不允许交叉。将风机位置的经纬度转化为坐标，根据风机坐标信息进行海缆交叉判断，其表达式为

式中：P1，P2和Q1，Q2为4个风机的坐标；・和○×分别表示点积和叉积计算。

⑤汇集变电站容量约束

海上风电场群的并网运行需要先汇集到海上升压站再进行输送，海上升压站的容量不小于各汇集电缆容量，其表达式为

式中：Si为电缆容量；Ni为汇集到升压站的电缆数量；Sasc为海上升压站的容量。

3 海上风电汇集系统模型求解算法

风机数量多，主要通过线缆和汇集电站汇集到海上升压站，其物理接线形式类似一个树形结构，将海上风机和电缆分别抽象成顶点和边，由于海上升压站是所有风机电能的汇集点，因此对于以最小生成树算法为基础的遗传算法优化模型而言，设置海上升压站为生成树的根节点，有利于简化求解过程获得最优解。对于汇集系统而言，拓扑结构主要由海缆成本所决定，海缆成本与其型号相关，海缆型号与其传输的功率相关，传输功率由拓扑结构确定，这就形成了海缆成本和拓扑结构相互耦合的过程，可以通过动态变权最小生成树（Dynamic Variable Weight Minimum Spanning Tree，DVW_MST）算法对遗传算法进行改进，求解得到海上风电场优化拓扑结构。

3.1 算法原理

使用动态变权最小生成树算法生成初始种群，DVW_MST算法的流程如图4所示。

图4 种群初始化流程Fig.4 The process of population initialization

交叉判定的具体步骤：每次使用DVW_MST进行选边时，按照净收益变化量大小对全部可选边进行排序，之后从净收益变化量最大的边开始，利用式（10）所给的交叉规避约束对模型的树形拓扑进行交叉识别，如果判定算法产生交叉线缆，则按照净收益大小排序依次寻找不产生交叉的次最优边；如果计算过程中未出现交叉线缆，则将此边添加进树形结构中。

动态边权是DVW_MST算法最重要的环节之一，建立动态边权最重要方法在于充分考虑海缆的建设成本和拓扑结构的耦合关系。算法过程首先需产生3个分别与树形拓扑相关的集合：集合U表示还没有纳入树形结构的风机、节点集合S中包括所有已经接入到树形结构中的风机、已经加入树形结构的边则存入节点集合E。具体DVW_MST算法大致可分解为以下几个步骤：①输入海上输电网络完全图G中的风机坐标作为顶点集合V以及输入输电线缆作为边的集合E，并初始化树形拓扑节点集合S，此时S只存入了以海上升压站为根节点的元素，即第一个元素为1的集合，用数学关系表达为U={i|i∊V，i≠1}，H≠Φ；同时初始化邻接矩阵AT为0；②在节点集合U中把一个未加入树形拓扑的第i个风机与树形拓扑集合S中的第j个风机关联，通过使用集电拓扑成本计算公式，建立连接后的成本变化量ΔCij；③通过比较挑选出ΔCij最小的顶点和相应连接的边，分别加入树形拓扑集合S和集合H中，生成新树的邻接矩阵AT。重复以上步骤，不断迭代更新集合U，S，E，直到遍历完所有完全图中的节点，所有集合U中的点清空并且风机坐标全都加入到了树形结构中，判断标准为点集S和点集V相等；④生成最小树，得到包括净收益和邻接矩阵A的输出结果，结束程序。

本文设计了一种新的链表编码方式，通过生成最小树形结构求解问题，反映了海上风电的优化问题，编写过程兼具了完整性和精确性。矩阵Am×n用来表示一个含有m行元素、n个节点的生成树。在本文的优化模型中m=3，第一行元素表示节点的连接情况，第二行表示节点负载的风机个数，第三行包含了两节点之间电缆的长度。在生成树矩阵中，每个“个体”，即每个风机点都有与之对应的信息。例如，生成树矩阵第一行第i个元素如果等于j，则表示第i个海缆节点与第j个海缆节点直接相连，并且电能的流通是单向的，通过节点i的电能必须流过节点j才能到达海上升压站；第二行第i个元素等于k，表示节点之间的负载有k个风机；同理第三行第i个元素等于d，表示节点间距为d。

为了判断遗传算法中种群个体的表现，需定义适应度函数以判断个体表现的优劣性。在本文中，成本较低的个体定义为优秀，成本较高的个体则为低劣。因此适应度函数可表示为成本的倒数，即：

本文使用精英选择、轮盘选择两种算子。精英选择保留最好种群中适应度函数最高的个体，直接进入下一次迭代，这样遗传算法的趋优性可以得到保障，并且加快遗传算法的收敛速度。

交叉算子是将两个个体进行叠加得到可行解空间，再利用DVW_MST算法在可行解空间中生成子树，从而得到子代。交叉算子的求解过程是模拟两个父代个体的染色体信息遗传给子代。在本文中父代的信息可以由邻接矩阵表示，任意两个父代生成树链表信息可表达为邻接矩阵。个体A1（3，n）和A2（3，n）的邻接矩阵B1（n，n）和B2（n，n）交叉重组得到结果B（n，n），再利用DVW_MST生成子代种群。

变异算子是在个体邻接矩阵中随机选择k条边加入邻接矩阵中，再利用动态变权最小生成树算法重新生成子代。父代个体A（n，3）的遗传信息同样可以转化为邻接矩阵B（n，n）。为了实现个体遗传信息的突变过程，在生成子代之前，在此个体邻接矩阵中加入任意条边p数得到。

3.2 计算流程

结合海上风电场的经济成本模型，采用上述的基于动态变权最小生成树的改进遗传算法，对海上风电场集群的汇集系统进行规划求解，分别进行初始种群生成、编码、适应度计算、选择、交叉、变异等操作，详细求解过程如图5所示。首先输入海上升压站和风电场坐标生成初始种群，其次分别计算各个风电场的净收益，通过适应度函数的处理，判断是否满足终止准则，如果不满足，则一步选取两个个体进行交叉变异，利用DVW_MST算法生成子树得到子代，重新迭代求解；如果满足，则输出种群作为最优个体，纳入最优解并进一步产生效果更好的下一代种群。

图5 改进遗传算法整体流程Fig.5 The overall process of improved genetic algorithm

4 案例分析

4.1 海上风机拓扑优化

为了验证本文所建模型和所提算法的有效性，选取江苏某地区正在规划的3种风电场拓扑结构为例，其集电海缆经济参数如表1所示[16]。拓扑结构如图6所示。

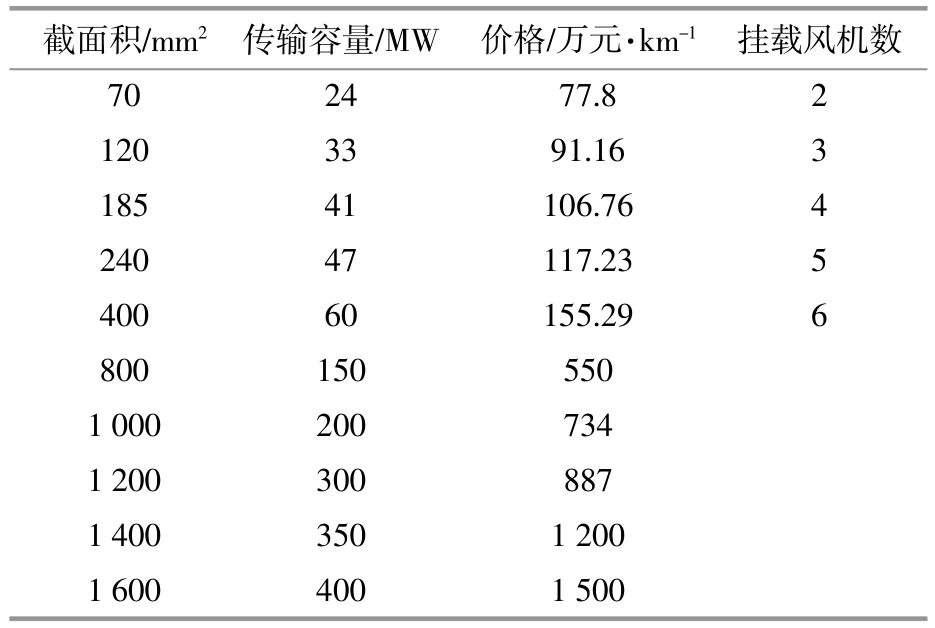
表1 集电海缆经济技术参数Table 1 Economic and technical parameters of collector submarine

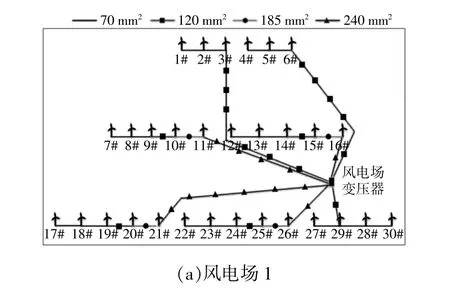
图6 风电场风机拓扑Fig.6 Wind farm turbine topology

针对上述3种拓扑结构进行优化，优化后的拓扑见图7，优化结果如表2，3所示。

表2 拓扑优化前后线路长度对比Table 2 Comparison of line length before and after topology optimization

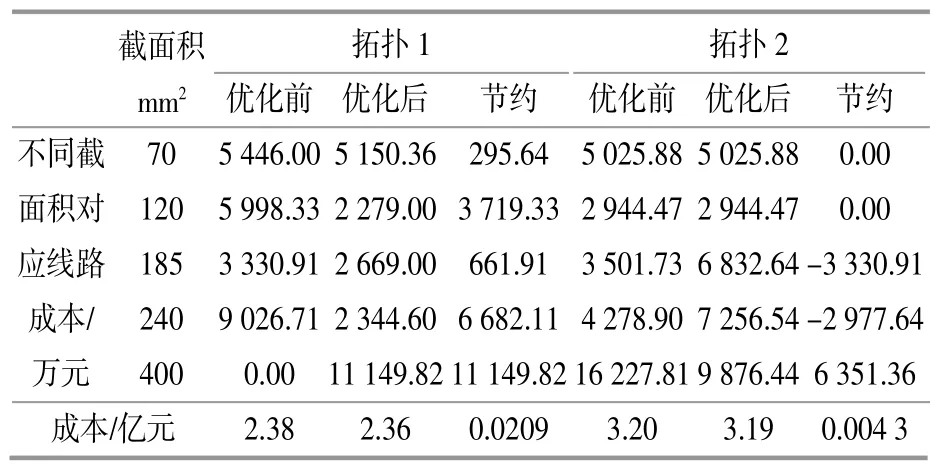
表3 拓扑优化前后技术经济成本对比Table 3 Comparison of technical and economic costs before and after topology optimization

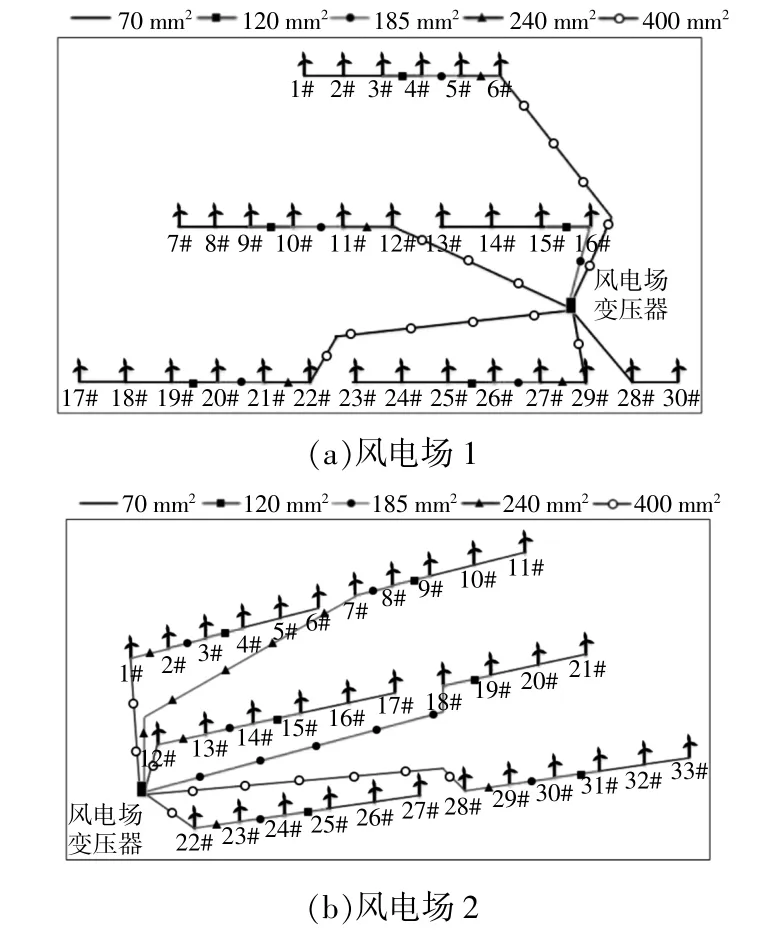
图7 风电场风机拓扑的优化结果Fig.7 Optimization results of wind turbine topology in wind farm

通过优化结果可知，拓扑3的结构未发生变化，所需成本均为3.636 9亿元，验证了本文所提智能算法与实际工程经验结果一致。拓扑1，2的优化结果与现有规划方案不同，在相同功率传输的约束下，本文所提优化算法成本更低，资产利用率更高。通过本文所提优化算法，拓扑1增加了71.8 km截面积为400 mm2的大功率传输电缆，但是减少了107.8 km的小功率传输电缆，提升了现有传输线路的资产利用率，并且降低了工程总投资，线缆成本减少了209万元，提升了系统经济性。拓扑2通过优化风机分组，提升了汇集电缆传输功率，虽然增加了56.6 km的较小截面积电缆，但是减少了40.9 km截面积为400 mm2的大功率传输电缆，增加了线缆利用率，线缆成本减少了43万元。说明本文所提出的方法能够对风电场风机拓扑进行有效优化，提高设备利用率，降低成本。

4.2 风电集群拓扑优化

本文以江苏某地区7个海上风电场为对象，相关参数如表1。对7个风电场的经纬度进行换算，得到风电场的地理位置信息，陆上升压站设在（100，100）处，具体如表4所示。

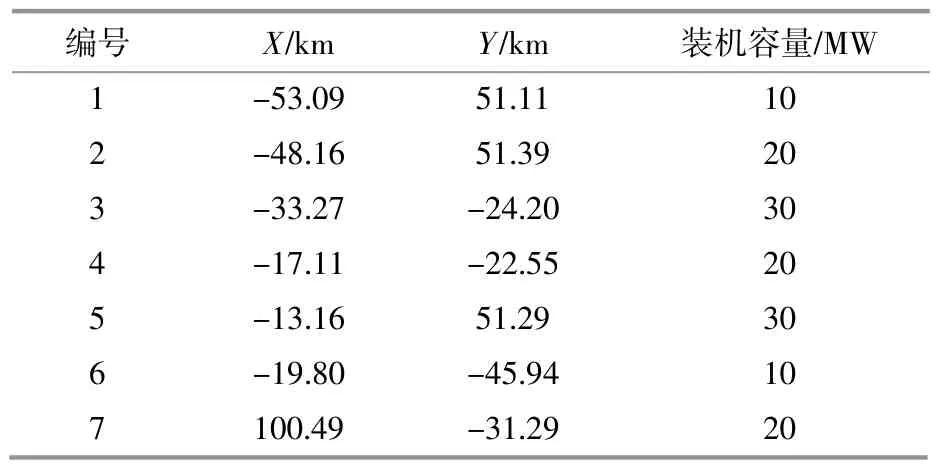
表4 风电场位置信息Table 4 Wind farm location information

风电场的出力信息利用风电场历史出力数据进行截取，作为其场景年的年出力数据，同时也反映了风电场集群内部的相关性信息。同时给定输电价格及投资信息：输电价格为0.08元/（kW・h），因输电有功功率限制而导致风电场弃电的补偿电价为0.32元/（kW・h），集电系统使用寿命为20 a，基准折现率为0.08。

使用本文所提出的基于DVW_MST的改进遗传算法对优化模型进行求解，海上升压站位置经过优化得到坐标为（0，35），拓扑优化结果如图8所示。图中，风车为风电场，黑色方块分别为海上升压站和陆上升压站。

图8 海上风电集成系统拓扑优化结果Fig.8 Topology optimization of offshore wind power system

将各个风电场直接接入海上升压站默认坐标（0，0），再通过海上升压站与陆上升压站的连接方式与本文优化后的结果进行对比，对比结果如表5所示。

表5 风电集群拓扑优化前后技术经济成本对比Table 5 Comparison of technical and economic costs of wind power cluster topology before and after optimization

由表5可知，使用本文的改进遗传算法后，集电系统线缆长度由563.1 km减少到416.3 km，通过适当减少截面积较小的240 mm2和800 mm2的线缆，改用截面积更大的400 mm2和1 600 mm2的截面线缆，能够对各风电场出力进行汇集输送，避免为了满足单个风电场传输需求而采用多条小功率电缆，从而提高线路利用率。改进风电场的汇集方式后，系统成本从31亿元降低至25.78亿元，成本降低了16.84%，集电系统的收益从10.35亿元提升至15.5亿元，总体收益提高5.15亿元。

最后，为了验证本文所提改进遗传算法的寻优寻优效果，采用传统遗传算法对上述优化模型进行求解，统计不同迭代次数中得到最优解的次数如图9所示。

图9 改进算法和传统算法效率对比Fig.9 Comparison of the efficiency of the proposed improved algorithm

由图9可知，与传统的遗传算法相比，本文所提的改进遗传算法在相同迭代次数中，获得最优解的次数明显更多。

5 结论

本文考虑了海上风电出力在空间上的互补特性，并综合考虑多种约束条件，提出了一种海上风电场汇集系统拓扑优化方法。算例结果表明：①多个风电场的平滑效应使风电场集群的最大出力降低，持续出力曲线更加平缓；②风电场或风电场集群的送出线路的优化容量通常低于其装机容量；③本文优化后得到的拓扑结构相比传统直接连接所得拓扑结构成本明显降低，净收益显著提高。验证了改进遗传算法的可行性，体现了本文所提出模型的有效性。