新型槽式太阳能真空吸热管设计方法及其光学性能研究

余强，单文玺，李自豪，雷东强

（1.中国农业大学 信息与电气工程学院，北京 100083；2.中国科学院电工研究所，北京 100190）

0 引言

太阳能作为一种典型的绿色清洁能源,近几十年来备受人们关注。太阳能热发电技术是太阳能利用的重要方式之一，其技术形式有塔式、槽式、碟式和线性菲涅尔式4种[1]，其中，槽式太阳能热发电技术最为成熟，其装机容量远高于其它3种技术形式[2]。聚光集热子系统作为槽式太阳能热发电系统的核心，主要由许多槽式太阳能集热单元组成[3]，而槽式太阳能真空吸热管是子系统最关键的设备，对其结构作出的优化和改进均可以提高系统的能量输出[4]。现阶段大多槽式太阳能热发电站运行温度不超过400℃，其热电转换效率因运行温度限制无法得到进一步提高[5]。对此可通过提高槽式太阳能集热器的聚光比（能流密度值与太阳辐照强度的比值）来提高槽式集热器的集热温度，该方法较其它方法相对简单、成本可控，成为了目前提高槽式太阳能集热温度的主要发展方向。国内外许多学者针对槽式集热器进行了大量研究。郑宏飞[6]提出了一种新型的多曲面复合槽式太阳能集热器方案，其在高温段效率有所提升。Rao B N[7]基于有限元及蒙特卡洛法对各种情况下的一次聚光器的结构进行优化从而提升其性能。还有学者通过在真空吸热管外加装二次聚光器来提高槽式太阳能集热器性能，如Tang X Y[8]和Shajan S[9]在真空吸热管上方设计并加入二次聚光器从而改善真空吸热管表面能流密度分布不均匀的问题。Bellos E[10]在槽式集热器的末端添加一种垂直式的二次聚光器来收集入射角不为0°时从末端逸出的光线，从而提高集热效率。还有专家学者对真空吸热管进行改进。Hou Y[11]将真空吸热管替换成一种平板接收器并验证了其可行性。王志敏[12]将真空吸热管替换成倒梯形腔口接收器并进行热性能模拟研究。姚磐[5]提出一种含以圆弧为微元段的自适应设计方法，设计出二次聚光器的新型槽式真空吸热管，既可以提高聚光比，又可以改善能流密度分布，从而提升集热效率。

前人研究少有在保证光学效率的同时，改善能流密度分布并提高聚光比的设计和措施。本文设计出一种新型的含双曲线型二次聚光器的真空吸热管，通过以减小金属内管直径、下移并加装二次聚光器来达到提高聚光比、改善能流密度分布的效果，并运用边界条件来完成双曲线型二次聚光器的设计，保证新装置的光学效率，最后搭建相应的聚光数学模型进行分析并与传统真空吸热管进行对比，验证其性能的优越性。

1 槽式集热器性能分析

1.1 光路分析

槽式太阳能集热器主要由槽式聚光器、真空吸热管、以及跟踪系统等组成，如图1所示。

图1 槽式太阳能集热器Fig.1 Solar parabolic trough collector

提高吸热管表面的几何聚光比可有效提高集热温度从而提高效率。由前文可知，目前提高聚光比主要有两种方式：一种是对槽式聚光器的结构进行调整；另外一种是优化槽式真空吸热管的结构。本文选择第二种方式。槽式集热器光线传播路径如图2所示。

图2 光线传播路径Fig.2 Propagating path of incident lights

相比于传统的槽式集热器，通过减小金属内管直径可提高聚光比，但同时会因此导致由一次聚光器反射出的部分光线从金属内管周围逸出，为保证其光学效率及改善其能流密度分布的均匀程度，可考虑将金属内管下移使得反射逸出的部分光线仅从金属内管上方逸出，并在金属内管上方加装二次聚光器来收集逸出的光线，再将逸出的光线反射至金属内管上表面。

1.2 金属内管位置下移以及管径减小对槽式太阳能集热器光学性能的影响

为验证减小金属内管直径可提高聚光比，基于本文作者前期研究成果[13]，利用蒙特卡洛光线追迹法（MCRT），以我国首个兆瓦级北京延庆槽式太阳能光热实验电站的传统槽式集热器为研究对象，进行建模分析（其参数见表1），具体的建模方法以及模型准确性的验证可参考文献[13]，本文不再赘述。在建模过程中，选择“东西跟踪，南北布置”的方式布置传统槽式集热器，具体计算时间取2022年6月21日（夏至日）正午12点。本文用周向能流密度表示金属内管上的光线分布，能流密度为单位面积收集到的太阳光能量，计算能流密度需预设太阳辐射强度（Direct Normal Irradiance，DNI），为简化计算取1 000 W/m2，仿真得到的能流密度分布如图3所示。

表1 北京延庆槽式太阳能集热器主要参数Table 1 Main parameters of Beijing Yanqing solar parabolic trough collector

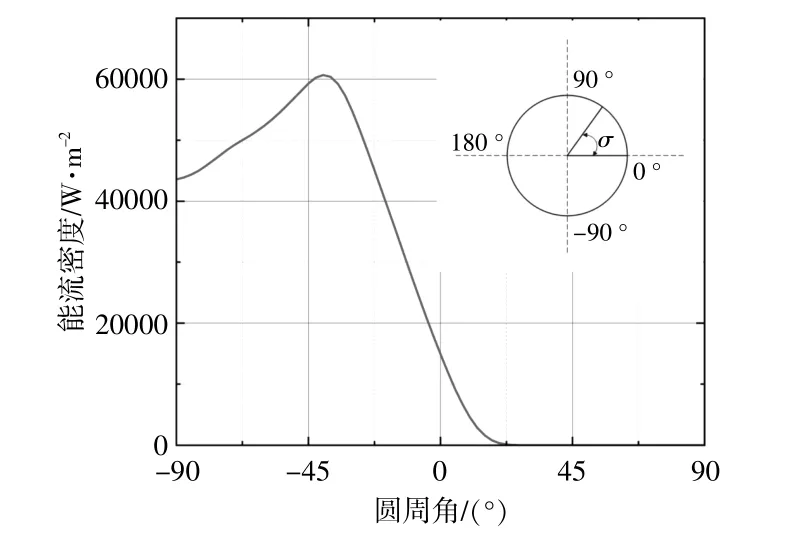
图3 槽式太阳能集热器能流密度分布Fig.3 Diagram of solar flux distribution

为分析金属内管直径大小对聚光性能的影响，针对北京延庆槽式太阳能集热器，在传统槽式太阳能真空吸热管布置以及其它参数保持不变的基础上，分别对不同金属管直径表面的能流密度分布进行分析，其结果如图4所示。

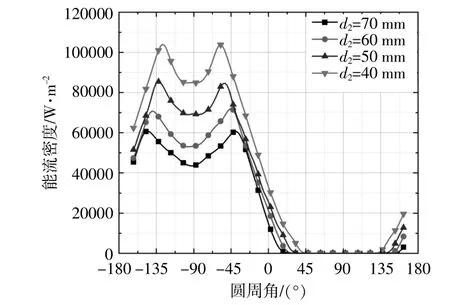
图4 金属管减小至不同直径的能流密度分布Fig.4 Diagram of solar flux distribution of metal tube reduced to different diameters

由图4可以看出，金属管直径的减小可提高聚光比（能流密度值与太阳辐照强度的比值），峰值处可由60 kW/m2提升至103 kW/m2。且经计算能流密度分布均匀度可从4.32%提升至13.3%，在一定程度上改善了能流密度分布。

为分析金属管下移对聚光性能的影响，以4 mm步长进行计算、分析，其结果如图5所示。

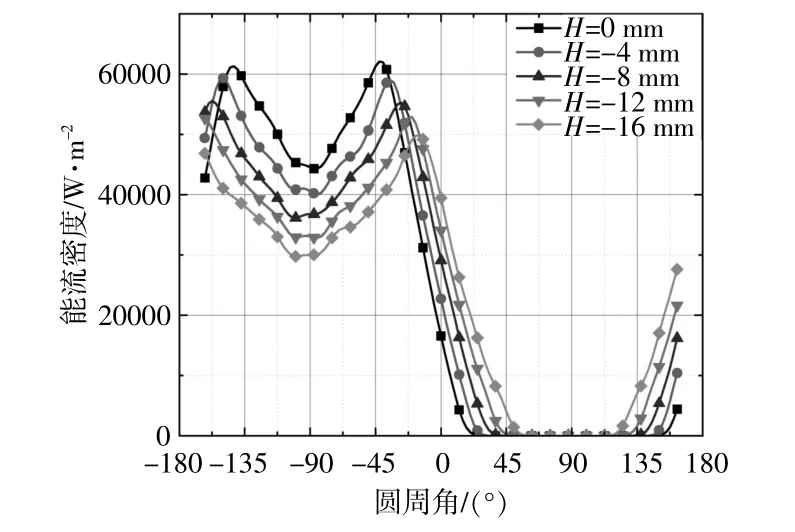
图5 金属管下移不同距离时的能流密度分布Fig.5 Solar flux distribution diagram of metal tube moved down at different distances

由图5可以看出，由于金属管布置位置下移，能流密度峰值向金属内管正下方的两侧（-180°及0°）移动，且金属内管上方可收集到更多的光线，较好地改善能流密度分布均匀度，经计算提升至35.66%；然而聚光比会相应地降低，峰值处由62 kW/m2降至49 kW/m2。综合衡量减小管径和下移布置对提高聚光比是可行的，但金属管下移会削弱金属管径减小带来的能量收益，因此，有必要在此基础上进行进一步优化。

2 新型槽式太阳能真空吸热管设计

2.1 金属管直径

考虑市场实际情况，本文在管径方面不作优化，实际选取市场已有的40 mm[14]作为减小后的金属内管。

2.2 金属管位置

金属管位置的确定过程如图6所示。

图6 金属管位置的确定过程Fig.6 Determining process of the position of the metal tube

在确定金属管位置时,需先求解一次聚光器边界处入射光线反射与竖直方向的最大夹角φ。以一次聚光器的中心点为原点建立平面坐标系，计算出边界处太阳光锥边界光线与竖直方向的夹角φ1，考虑到槽式太阳能集热器的误差，换算成与竖直方向的夹角φs为0.4°[15]，计算式为

式中：θ为太阳光锥角。

然后计算出边界处垂直入射的光线经一次聚光器反射后与竖直方向的夹角φ2，计算式为

式中：f为一次聚光器（槽式抛物面）的焦距；W为槽口宽度。

边界光线经一次聚光器反射后与竖直方向的夹角φ的计算式为

根据边缘光线理论，考虑一次聚光器边界处光线反射后的路径与金属管下方相切时,保证垂直于槽式太阳能集热器入射的全部光线不会从金属管下方逸出，只会射入金属管或从金属管上方逸出，即可得到金属管的具体位置的计算式为

式中：金属管圆心坐标为（0，ym）；rm为金属内管半径；yb为一次聚光器边缘点的纵坐标。

最后得到金属内管的参数：当金属管直径为0.04 m，即rm=0.02 m，计算得出金属管圆心位置为（0，1.695 8），下移0.014 2 m。

2.3 二次聚光器的设计

为了能够回收从金属管上方逸出的光线，本文设计了一种双曲线型的二次聚光器，见图7。

图7 二次聚光器设计示意图Fig.7 Schematic diagram of secondary concentrating design

①在一次抛物面槽式聚光器的边界点处取金属内管上表面切线，在切线上取二次聚光器的边界点（xb，yb），可确保所有在经过一次聚光器反射后未被金属管吸收的光线可被二次聚光器收集。

②本文中光学效率为金属内管吸收的总辐射能量与垂直入射到槽式太阳能集热器采光口面积上的太阳直射辐射能之比。为提高光学效率，即减少二次聚光器对二次聚光器上方垂直入射光线的遮挡，且考虑对称性以及防止反射光线被二次聚光器遮挡，取两条距金属管圆心最远处切线中与①中切线相交得到的较高点为二次聚光器的边界点（xsrb，ysrb）。

③为确保二次聚光器反射光线能够入射至金属内管上，焦点越远离金属内管中心处，二次聚光器的聚光效果越好，根据双曲线的性质，双曲线的焦点（xf，yf）取至与边界点同一水平位置处。

由上述步骤即可计算出二次聚光器的双曲线方程。

过边界点作金属内管上表面的切线的斜率kb（以右侧为例），则kb表达式为

式中：yr为金属管圆心位于所建立的二维平面的y值；（xb，yb）为边界点的坐标值。

二次聚光器边界点可表示为

由此可计算出ysrb=1.719 6。

假设双曲线型二次聚光器顶点坐标为（xtop，ytop），焦点坐标为（xf，yf），可设该二次聚光器的方程为

式中：a，b，c为求解双曲线方程时预设的未知数。

推导出顶点与焦点二者关系为

由双曲线的性质可知：

由式（7），（8）和（9）联合求解，可以计算出式（7）中的参数分别为a=0.99，b=0.140 8，c=1，带入式（7），（8），计算出顶点（xtop，ytop）为（0，1.729 6），同时可计算得到双曲线方程（取下半支），即：

2.4 新型真空吸热管设计结果

经前文计算，可得到新型槽式太阳能真空吸热管结构，如图8，9所示。具体参数见表2[5]。

表2 新型槽式太阳能真空吸热管参数Table 2 Parameters of the new vacuum absorber tube

图8 含二次聚光器的真空吸热管二维视图Fig.8 Two-dimensional view of vacuum absorber tube with secondary concentrator

图9 含二次聚光器的真空吸热管三维视图Fig.9 Three-dimensional view of vacuum absorber tube with secondary concentrator

3 新型真空吸热管槽式集热器数学模型建立

为研究新型真空吸热管槽式集热器的聚光性能，本文利用经过验证的传统槽式集热器的建模方法,建立含二次聚光器的真空吸热管新型槽式太阳能集热器的光学仿真模型，建模流程图如图10所示。

图10 新型槽式太阳能集热器光学仿真流程图Fig.10 Simulation flow chart of new parabolic trough collector

除在光线从金属管上方垂直入射至二次聚光器上时被遮挡光线不予统计外，入射至二次聚光器前的光线传播路径与传统槽式太阳能集热器的光线传播路径基本一致，如图11所示，具体数学计算过程如下。

图11 经二次聚光器反射后新光线方程计算示意图Fig.11 Calculation of the path of the new light after reflection by the secondary concentrator

用一次聚光器反射后的光线方程和二次聚光器方程联立后计算出交点（xp3，yp3），计算式如下：

式中：（x0，y0）为入射光线入射至一次聚光器上的具体位置；k1为经一次聚光器反射后光线的斜率。

不是所有的入射光线都能被槽式聚光器吸收，判断到达二次聚光器光线是否会因光线入射角逸出平面的方法如图12所示。

图12 判断到达二次聚光器光线是否会因光线入射角溢出平面计算示意图Fig.12 Calculation diagram to determine whether the light arriving at the secondary concentrator will spill out of the plane due to the angle of incidence of the light

用式（12）判断是否因为入射角过大而导致光线逸出新型槽式集热器。

式中：L为一次聚光器长度；α为太阳光线入射角。

若光线不逸出，则计算光线经双曲线型二次聚光器的反射光线。以入射至左半边的光线为例，计算过程如下。

式中：ks为交点处二次聚光器方程切线的斜率；θsv为过交点作切线的垂线与x轴正方向的夹角；θ2为经二次聚光器反射后的光线与x轴正方向的夹角；k2为经二次聚光器反射后光线方程的斜率。

最后可计算出经二次聚光器反射后的光线方程：

判断反射光线是否与金属管相交，若相交可计算其交点，表达式为

计算得到交点（xp4，yp4），利用交点判断光线是否会因为光线入射角过大而逸出槽式太阳能集热器，其表达式为

若式（19）成立，则不会逸出，即可统计光线的位置，并用以下公式计算出有关光学性能指标。

根据光线位置统计金属管周向的能流密度，每5°为一间隔进行统计得到光线数量p，并根据能流密度定义推导出金属管周向能流密度值Iσ：

式中：Sc为槽式太阳能聚光器的弧面面积；Sm为圆柱形金属内管的侧面积；pt生成的随机点总数。

槽式太阳能集热的光学效率为真空吸热管吸收的总能量与垂直入射至槽式太阳能集热器上的太阳辐射能量之比[17]，表达式为

式中：Qc为真空吸热管吸收的总能量；S为槽式太阳能集热器的采光口面积；ω为二维平面内直射太阳光线与聚光器采光平面法向间的夹角。

能流密度分布均匀度ΔI体现能流密度分布的均匀程度，由定义可推导出。

式中：Ia为金属管周向能流密度平均值。

4 性能分析与讨论

经计算，可得到新型槽式太阳能集热器的金属管周向能流密度分布图、光学效率及能流密度均匀度等有关光学性能指标。

金属管周向能流密度分布如图13所示。

图13 传统与新型能流密度分布对比Fig.13 Comparison diagram of solar flux distribution between traditional and new structureflux distribution

由图13可以看出，在金属管的下半表面，由于金属管直径减小，即使在金属管下移的影响下，聚光比仍有提高，能流密度的峰值在金属管上表面，峰值所处位置从圆周的-42.5°变为-17.5°，能流密度峰值从62.11 kW/m2提高至71.43 kW/m2。从金属管上表面来看，双曲线型二次聚光器的聚光效果与一次聚光器类似，其能流密度分布的曲线形状均为“马鞍形”，同时下表面也产生两个峰值，分别在30°和147.5 °的位置，且能流密度分布均匀度从4.32%提升至59.37%，表明金属管周向的能量分布更加均匀，这将会在保证其安全性的前提下减少金属管的热量损失。

传统与新型槽式太阳能集热器光学性能对比见表3。

由于加入二次聚光器，光学效率会有所下降，其原因是：①二次聚光器遮挡住入射光线；②光线到达二次聚光器时会被部分吸收；③部分光线会由于二次聚光器反射出槽式集热器。光学效率的下降导致最终到达金属管表面的总能量会有所下降，但下降较少。

5 结论

本文基于MCRT，利用MATLAB对装有传统真空吸热管的槽式集热器进行建模研究，并在此基础上探究金属管下移和金属管直径减小对槽式太阳能集热器光学性能的影响。在保证光学效率的情况下，为了在提高聚光比的同时还能改善能流密度分布，推导出计算双曲线型二次聚光器的方程，设计出含双曲线型二次聚光器的真空吸热管，对装有新型真空吸热管的槽式太阳能集热器进行建模，并与传统槽式集热器进行对比分析。得出如下结论。

①在传统槽式集热器中，金属内管直径由70 mm减小至40 mm时，峰值处聚光比可由60 kW/m2提升至103 kW/m2，能流密度分布均匀度可从4.32%提升至13.3%。

②在传统槽式集热器中，金属内管由焦点处下移16 mm，可将能流密度分布均匀度提升至35.66%，峰值处聚光比由62 kW/m2下降至49 kW/m2。

③对比传统槽式集热器，本文设计的新型槽式集热器在光学效率仅下降1.88%的情况下，聚光比峰值从62 kW/m2提高到了71 kW/m2，同时改善了55.05%的能流密度分布均匀度。