降雨-蒸发作用下土石坝渗流场及坝坡稳定性研究
吴 凡 王从锋 王云峰
(三峡大学 三峡水库生态系统湖北省野外科学观测研究站, 湖北 宜昌 443002)
降雨是诱发土质边坡产生滑坡的主要因素,降雨入渗会导致非饱和土渗透力的增加与基质吸力的降低,从而降低边坡的稳定性安全系数,导致边坡出现破坏[1].研究降雨对土质边坡稳定性的影响,实际上就是研究非饱和土的渗透特性对土体强度的影响[2],而降雨入渗到非饱和土中属于瞬态变化的过程,每一时刻体积含水量都在发生变化,所对应基质吸力和渗透系数同样在时刻变化[3].关于降雨对边坡稳定性的影响目前开展了不少研究,如邱祥等[4]分析了降雨条件下边坡暂态饱和区形成条件,研究降雨强度、饱和渗透系数、坡度等多因素对边坡暂态饱和区演化特征的影响;关晓迪等[5]比较了边坡土体在不同降雨强度与坡比条件下的降雨入渗差异;王宁伟等[6]结合饱和-非饱和渗流理论,研究了不同降雨类型下边坡渗流场的变化规律,探究了边坡稳定性安全系数与降雨循环次数的关系.
目前大多数边坡稳定性研究仅考虑降雨这单一因素,对于降雨-蒸发作用下边坡渗流场及边坡稳定性变化规律的研究相对较少,这是由于边坡在复合天气因素作用下的水分迁移运动规律难以掌握.如杨国强等[7]在进行降雨入渗的数值模拟时,应用的是单位流量边界条件,该边界条件是根据降雨强度来设定入渗流量会无损失的加载到坡体中,是一种进行简化处理的理想工况.而实际情况中,除去降雨入渗的影响,还需要根据环境因素来考虑蒸发作用对渗流场及稳定性的影响.另外,关于土石坝在降雨-蒸发作用下的稳定性研究也较少,因此研究在降雨-蒸发作用下土石坝的渗流场和坝坡稳定性变化很有必要.
本文以华南地区某土石坝为主要研究对象,采用Geo-Studio有限元计算软件,基于实测气象资料,分析降雨-蒸发作用下土石坝的渗流场与坝坡稳定性变化,以期为土石坝坝坡的防护、运行与监测提供一定参考.
1 非饱和计算理论
1.1 非饱和土渗流理论
降雨入渗过程是土体从非饱和状态到饱和状态的过程,其渗流过程符合达西定律.选取一微小单元土体,根据渗流连续性条件以及达西定律可得到降雨入渗条件下的渗流微分方程[8]:
式中:K x(hm)、K y(hm)、K z(hm)为关于基质吸力的各方向非饱和渗透系数;Q为施加的边界流量;hw为基质吸力水头;θ为体积含水量.
1.2 非饱和土抗剪强度理论
Fredlund等[9]基于非饱和土的双应力应变理论,提出了非饱和土的抗剪强度公式:
式中:c'为有效黏聚力;σn为法向应力;φ'为有效内摩擦角;φb为与基质吸力相关的摩擦角;(ua-uw)为基质吸力.
1.3 边界条件
土地气候相互作用边界条件,是将表示降雨入渗与蒸发的流量边界条件相互叠加的边界条件,即综合考虑降雨量、空气温度、相对湿度、风速和太阳净辐射能量等相互作用下的模拟条件.其表达式为
式中:P为实际降雨量;E v为土体蒸发量.
Penman结合相对湿度、空气温度、风速和太阳净辐射能量等气象因素,根据能量守恒定律提出Penman蒸发公式:
式中:Γ为饱和蒸气压与温度关系曲线的斜率;R a为土表面净辐射量;E a为自由水面蒸发量;L为蒸发潜热;η为 湿 度 常 数.
为计算非饱和土表面实际蒸发量,Wilson 改进了Penman蒸发公式,即Penman-Wilson公式:
式中:E b为自由水面蒸发量;B为空气相对湿度倒数;A为土体蒸发面上相对湿度倒数;f(u)为风函数,f(u)=0.35(1+0.15u);u为风速;e a为土体表面空气的蒸汽压.
当考虑温度作用时,土表面温度可由Wilson公式确定:
式中:T a为土体表面空气温度.
以上方程构成了非饱和土考虑降雨与蒸发作用的理论模型[10].
2 数值分析模型
2.1 模型建立
依据地质勘测资料与工程实际需求,本文以主坝最大断面建立模型,如图1所示.采用三角形与四边形单元的非结构化网格,共计8 197个单元,8 440个节点.主坝迎水坡面采用混凝土面板护坡,坝顶已水泥硬化,故在下游坝坡、排水棱体以及地基连接段加载土地气候相互作用边界条件,该边界条件受降雨和蒸发的控制.砂质黏性土层、基岩、防渗墙和排水棱体考虑为仅限饱和模型,坝体填土考虑为饱和-非饱和模型.
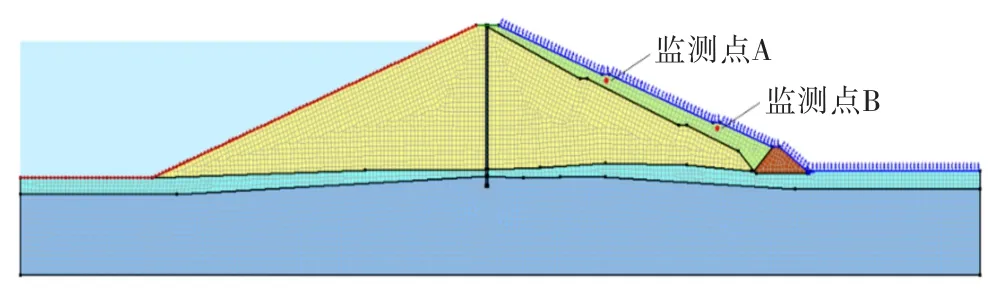
图1 计算模型
发生降雨时,当降雨强度小于土体渗透率时按流量边界处理,其大小可取降雨强度;当降雨强度大于土体渗透率时,部分雨水会沿坝坡面向坝脚处汇集,并在坝坡表面形成一层薄水膜,此时边界可按定水头边界进行处理,其大小可取为地表高程.考虑蒸发时,按Penman-Wilson模型来度量气象参数.
2.2 计算参数
各材料的力学参数依据大坝历次地质勘探、注水试验及文献[11]进行选取,见表1.

表1 材料力学性质参数
土水特征曲线是用来表示体积含水量与基质吸力之间的关系,新、旧坝体填土的土水特征曲线如图2所示.本文采用Fredlund-Xing模型求取非饱和土体积含水量函数.在已知土体的饱和体积含水量的情况下,估算渗透系数函数[12-13]:
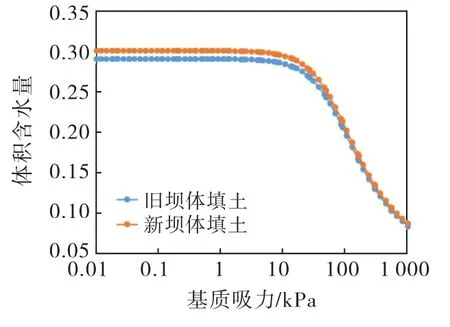
图2 坝体填土的土水特征曲线
式中:kw为负孔隙水压力所对应的渗透系数;ks为饱和渗透系数;N为最大负孔隙水压力;j为最小负孔隙水压力;ψ为对应第j步的负孔隙水压力;y为虚拟变量;θ0为方程的起始值.
气象参数主要包括降雨量、大气温度、相对湿度、平均风速与太阳净辐射能量,其也是土体-气候相互作用对土质边坡稳定性产生影响的主要因素[14].根据库区水文气象观测站与国家气象数据中心的数据资料(2002—2021年),库区多年平均气温为22.8℃.本地区多年平均湿度76.75%,变化范围在53%~92%之间.受东南季风影响,风向不稳定,多年平均风速为2.36 m/s.太阳净辐射能量可由Geo-Studio软件中模块自带公式进行计算.
根据国家气象局颁布的降水强度等级划分标准,由24小时降水量可将降雨划分为小雨(0,10]、中雨(10,25]、大雨(25,50]、暴雨(50,100]、大暴雨(100,250]、特大暴雨(>250)mm/d.
为确保降雨量选择的时效性,统计库区2019至2021年月降雨量,如图3所示.

图3 2019—2021年库区各月降雨量分布
近三年降雨量均集中在汛期4到9月,选取2021年6月进行分析,该月最大日降雨量90 mm,降雨等级为暴雨,降雨分布如图4所示.
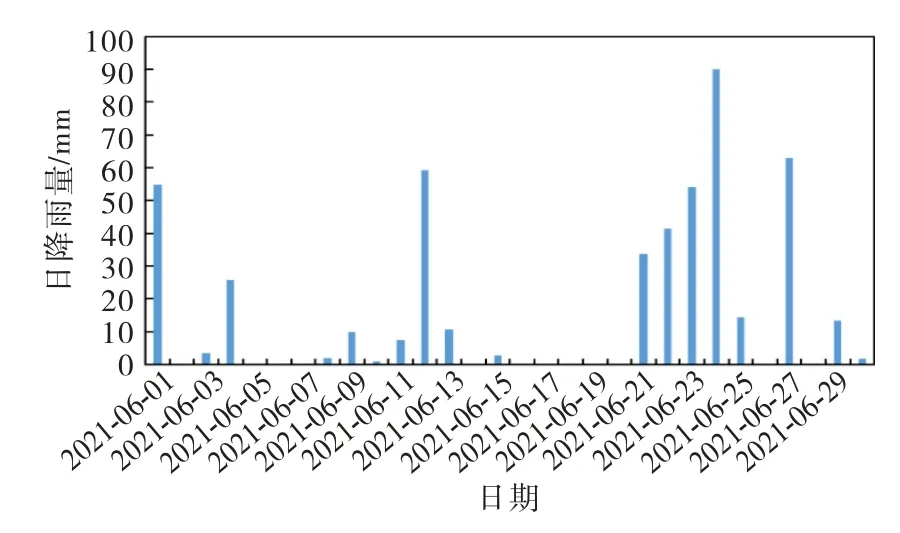
图4 2021年6月各日库区降雨量分布
2.3 计算工况
库区所属莲花山脉山地且邻近南海,易受台风影响,降雨强度变化大且多以单峰型为主,故设置降雨类型为递增型、递减型、集中型,降雨类型如图5 所示.根据2021年6月库区降雨量分布,设置大雨和暴雨两个降雨等级,降雨强度分别为48和96 mm/d,设置降雨历时为24 h,雨停时间为24 h,总历时48 h.
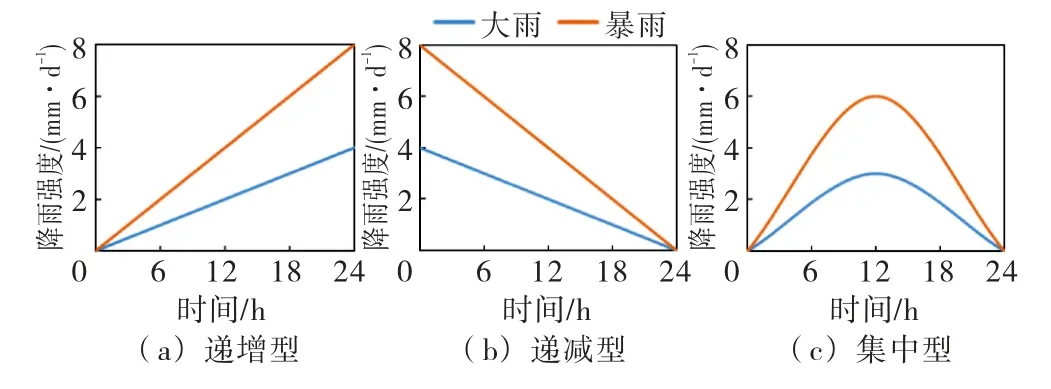
图5 降雨类型
3 计算结果与分析
3.1 渗流场影响分析
3.1.1 不同降雨类型分析
在降雨入渗的过程中,坝坡表层土体最先受到影响,其抗剪强度发生改变,故监测点A 与B位于坝坡面1 m 深处.以降雨等级为大雨为例,监测点A、B处不同降雨类型的孔隙水压力随时间变化的情况,如图6所示.

图6 各降雨类型孔隙水压力变化
在降雨入渗的作用下,监测点A 与B 处土体孔隙水压力随降雨时间的增加而呈现上升趋势,当降雨停止后,孔隙水压力开始逐渐降低.不同降雨类型在降雨过程中孔隙水压力表现出不同变化规律:对于递增型降雨,孔隙水压力的上升速率随降雨的持续而逐渐增大;对于递减型降雨,孔隙水压力的上升速率随降雨的持续而逐渐减小;对于集中型降雨,表层土体孔隙水压力的上升速率随着降雨的持续先增大、后减小.
当降雨时间相同时,递减型降雨孔隙水压力都会先达到最大值,然后集中型降雨,最后是递增型降雨.递减型降雨的孔隙水压力变化幅度要大于其余两种降雨类型,变化幅度从大到小为:递减型>集中型>递增型.如监测点A 降雨第16 h,递减型降雨的孔隙水压力为-35.7kPa,增长率为35.1%;集中型为-42.9 k Pa,增长率为22.0%;递增型为-50.1 k Pa,增长率为8.9%.
降雨第24 h后,递增型降雨孔隙水压力仍会出现小幅度的增加,相对于其余降雨类型孔隙水压力达到最大值的时间表现为“滞后性”.这是因为第24 h时递增型降雨的降雨强度达到最大,降雨量也达到最大,降雨停止后滞留在坝坡表面的雨水在重力与水力梯度的作用下仍向坝体内部入渗,导致孔隙水水压力的增加.
3.1.2 不同边界条件分析
以降雨等级为大雨为例,不同边界条件下土石坝渗流场的变化规律,如图7所示.
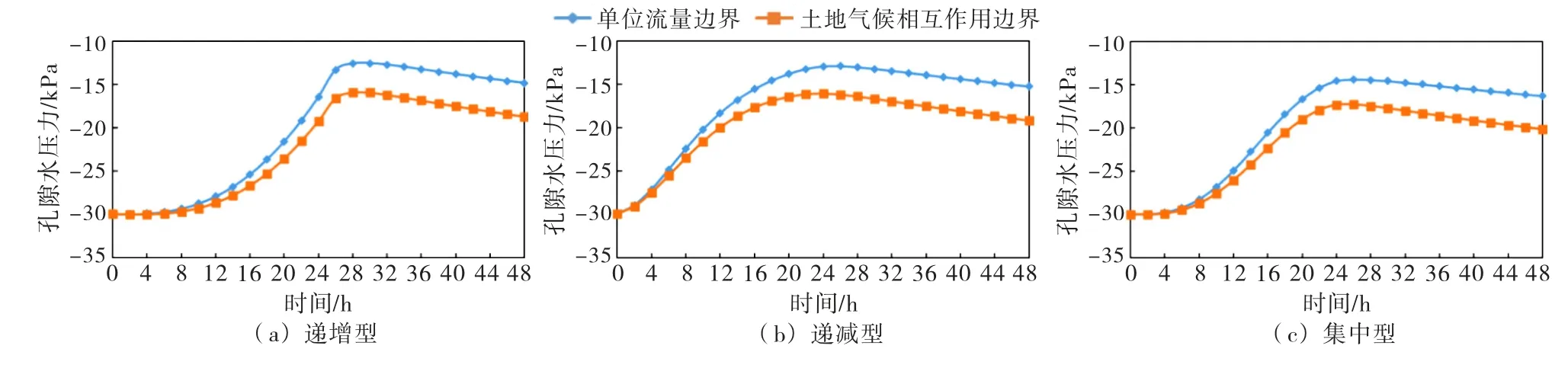
图7 各雨型不同边界条件安全系数变化
土地气候相互作用边界条件下,各降雨类型下土体孔隙水压力的大小与增长速率均要小于单位流量边界条件;当降雨停止时,部分滞留在坝坡表层的雨水蒸发消散,导致入渗降雨的减少,表层土体的孔隙水压力的下降速率要大于单位流量边界条件.
考虑降雨入渗对土石坝渗流场的影响时,两种边界条件下不同降雨类型的孔隙水压力相差不大.对于递增型降雨,降雨第24 h孔隙水压力相差2.77 k Pa;对于递减型降雨,降雨第24 h孔隙水压力相差3.12 k Pa;对于集中型降雨,降雨第24 h孔隙水压力相差2.78 k Pa.当降雨停止时,受蒸发作用影响,两种边界条件的表层土体孔隙水压力之间的差值会越来越大,土地气候相互作用边界条件下的孔隙水压力会随着雨停的时间的增加而更快降低至初始状态.
3.2 坝坡稳定性分析
3.2.1 不同降雨类型分析
坝坡稳定性分析所采用参数与渗流计算参数保持一致,各降雨等级下不同降雨类型的边坡稳定性安全系数随时间的变化情况如图8所示.
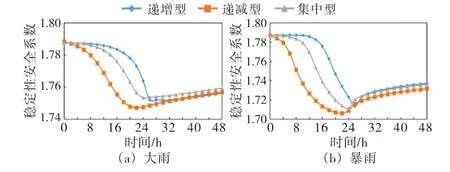
图8 各降雨等级不同雨型安全系数变化
在降雨入渗的作用下,安全系数随降雨时间的增加呈现下降趋势,当降雨停止后,安全系数会出现回升.不同降雨类型在降雨过程中安全系数表现出不同变化规律:对于递增型降雨,安全系数的下降速率随降雨的持续而逐渐增大;对于递减型降雨,安全系数的下降速率随降雨的持续而逐渐减小;对于集中型降雨,安全系数的下降速率随着降雨的持续先增大、后减小.
相同降雨时间下,递减型降雨的安全系数变化幅度要大于其余两种降雨类型,变化幅度从大到小为:递减型>集中型>递增型.安全系数的变化情况与孔隙水压力的变化相互对应,这是因为雨水从坝坡面渗入到坝体内部,会导致土体孔隙水压力升高.孔隙水压力越高,基质吸力就越低,进而导致土体抗剪强度的降低.同时,降雨等级越大,安全系数的变化范围也就越大.
3.2.2 不同边界条件分析
以降雨等级为大雨为例,不同边界条件下安全系数的变化规律,如图9所示.

图9 各雨型不同边界条件安全系数变化
土地气候相互作用边界条件下,递增型降雨的安全系数最小值为1.752,下降率为1.96%;递减型降雨的安全系数最小值为1.747,下降率为2.24%;对集中型降雨的安全系数最小值为1.754,下降率为1.84%.而单位流量边界条件下,递增型降雨的安全系数最小值为1.740,下降率为2.63%;递减型降雨的安全系数最小值为1.736,下降率为2.85%;对集中型降雨的安全系数最小值为1.741,下降率为2.57%.
可见,在降雨与蒸发作用条件下,当降雨类型为递减型时,安全系数的下降率最大,对于坝坡稳定性为最不利影响,此时应做好防护与监测工作.
土地气候相互作用边界条件下各降雨类型的安全系数降低速率要小于单位流量边界条件,但安全系数均要大于单位流量边界条件.这是因为土地气候相互作用边界条件对土体的影响主要集中在土体表层区域[15],考虑到蒸发作用的影响,部分降雨在还未渗透进坝体内部时被蒸发消散,导致入渗雨水比单位流量边界条件少,该边界条件下土体抗剪强度要更大,故安全系数大于单位流量边界条件.另外,降雨与蒸发作用是受到包括降雨、温度、相对湿度、风速和太阳辐射能量等多种气象要素共同影响的复杂过程.而坝坡的稳定性也会受到气象要素的影响,是因为土体表面和地下水位之间存在非饱和带,该区域的土体性质会受到土体与大气之间水分交换和能量传递的控制[16-17].降雨与蒸发作用条件下所反映的渗流场与稳定性变化更符合实际.
4 结 论
本文利用Geo-studio有限元软件对华南某水库进行土石坝渗流场与坝坡稳定性的数值模拟,得出如下结论:
1)不同降雨类型下表层土体孔隙水压力表现出不同变化规律:递增型降雨的孔隙水压力上升速率随降雨的持续而增大,递减型降雨减小,集中型降雨先增大后减小.稳定性安全系数的下降速率与孔隙水压力上升速率相对应.
2)相同降雨时间下,递减型降雨的孔隙水压力与稳定性安全系数的变化幅度要大于其余两种降雨类型,变化幅度从大到小为:递减型>集中型>递增型.
3)降雨与蒸发作用条件下,递减型降雨的安全系数的下降率最大,对于坝坡稳定性为最不利影响,应做好防护与监测工作.
4)土地气候相互作用边界条件下各降雨类型的孔隙水压力增长速率和安全系数降低速率均要小于单位流量边界条件,但安全系数均要大于单位流量边界条件,降雨与蒸发作用条件下所反映的渗流场与稳定性变化更符合实际.

