MCJ-UNet：一种双/多通道联合InSAR相位解缠网络

丁泽刚 孙 涛 王 震* 赵 健 史一鹏 陈浩龙 陈之洲 王 岩 曾 涛

①(北京理工大学信息与电子学院雷达技术研究所 北京 100081)

②(卫星导航电子信息技术教育部重点实验室(北京理工大学) 北京 100081)

③(北京理工大学重庆创新中心 重庆 401120)

1 引言

干涉合成孔径雷达[1,2](Interferometric Synthetic Aperture Radar,InSAR)测量是一种强大的微波遥感技术，可通过两(或多)幅存在空间基线的SAR图像来获取干涉相位，并基于相位信息解算目标高程，实现数字高程模型(Digital Elevation Model,DEM)的获取。

相位解缠(Phase Unwrapping,PU)是InSAR处理的核心环节，解缠质量将直接影响DEM产品的精度。就单通道(单频、单基线)相位解缠而言，其本质是一个病态问题。在单通道InSAR观测构型下，仅可获取目标场景的单一通道的干涉图，相位解缠需基于相邻像素的相位梯度积分进行。这一处理方式将严格受限于Itoh假设[3]，该假设要求相邻像素间的真实干涉相位差位于 (-π,π]区间，约束了相邻像素间的高程差。当目标场景的高程变化剧烈时，将出现相位欠采样问题，导致单通道相位解缠失败[4]。

近年来，以多频[5,6]、多基线[7]观测构型为代表的多通道InSAR技术迅速发展[8]，为上述问题的解决提供了有效途径。不同于单通道相位解缠的相位梯度积分处理，多通道InSAR可借助干涉通道自由度的提升，利用不同通道间的高程模糊度差异直接获取目标点的解缠相位，突破了Itoh假设的限制，有效提升了InSAR技术在测绘困难区域的适应性[9,10]。

目前，单通道相位解缠算法已较为成熟，主要包括路径积分类、最小二乘类、网络规划类等。随着多频、多基线InSAR系统的快速发展，多通道相位解缠算法也已经过了大量系统的验证，主要包括：基于干涉相位统计模型的最大似然估计(Maximum Likelihood Estimation,MLE)算法[11]、最大后验(Maximum a Posteriori,MAP)估计算法[12]等；基于干涉相位算数性质的中国余数定理(Chinese Remainder Theorem,CRT)算法[13]、聚类(Cluster Analysis,CA)算法[14]等；以及由单通道相位解缠思路拓展而来的基于MLE的相位梯度积分算法[15]、基于邻点集的相位梯度积分算法[16,17]、两级规划(Two-Stage Programming Approach,TSPA)算法[18]等。随着上述算法的迭代更新，相位解缠技术正向着高时效、高精度和强适应的方向发展。

随着高分辨、大幅宽InSAR系统的不断推出，大规模干涉图的高效解缠成为当前InSAR技术发展的瓶颈。因此，在处理效率方面具有突出优势的深度学习技术成为当前相位解缠方法研究的热点领域。目前的研究已经发展出部分可用于相位解缠的深度神经网络，如基于枝切法的深度学习解缠方法[19]、PGNet[20]及DLPU[21]等。但上述所提到的基于深度学习的解缠方法均基于单通道解缠思路，在噪声抑制及地形适应性方面仍有不足。在基于深度学习的多通道联合相位解缠网络方面，目前的研究较为有限，已有研究成果的典型代表为CANet[22]。该方法由CA算法拓展而来，通过深度卷积神经网络(Deep Convolutional Neural Network,DCNN)完成像素簇聚类处理，为基于深度学习的多通道联合相位解缠技术的可行性提供了例证。在该方法的处理中，并非将神经网络直接用于获取解缠相位或相位模糊数，而是用于完成聚类处理这一关键步骤。这一处理方式有效提升了聚类质量及效率，聚类结果则作为后续处理的输入，以便结合较为成熟的相位梯度积分类算法获取解缠相位。

作为多通道相位解缠与深度学习技术的另一种尝试，本文的研究则聚焦于基于多通道干涉相位直接获取相位模糊数，利用多通道相位间的相互约束进行解缠误差抑制，并采用尽量简单的后处理完成相位解缠。本文所提出的网络为多通道联合InSAR相位解缠网络(Multi-Channel-Joint-UNet,MCJUNet)，其构建的核心思路如下：首先，该网络聚焦模糊数估计这一相位解缠中的核心环节，将相位解缠问题转换为语义分割问题，并采用多输出UNet网络[23]完成对多通道模糊数的估计；其次，在网络各解码路径的输入和编码路径的输出之间，引入挤压激励模块(Squeeze-and-Excitation,SE)[24]动态调整特征信息权重，增强不同输出通道对其所需信息的感知能力；最后，利用多通道相位关系和网络输出模糊数概率的特点，构建了多通道联合约束下的相位残差优化损失函数，以增强网络对多通道相位特性的学习能力。此外，为避免语义分割结果在边缘区域的细节误差对解缠效果的影响，本文还提出一种基于多通道联合约束的解缠误差自修正方法，以保证解缠质量。

此外，需要说明的是，由于双通道与多通道联合相位解缠的机理及处理方法一致，本文针对MCJ-UNet的网络构建原理解释、网络架构描述以及实验验证等均是在典型的双通道(双频、双基线)构型下进行的。针对双通道向多通道相位解缠网络的拓展，本文也在相应部分进行了说明。

2 InSAR相位解缠原理

2.1 单通道相位解缠原理及其局限性

通过存在空间基线的两部SAR天线同时(或单部SAR天线重轨)观测，可获取同一场景的两幅SAR图像，并在此基础上提取干涉相位。InSAR处理的核心即为对干涉相位的处理，其本质是通过干涉相位重构精确的观测几何，并通过几何信息解算高程。其中，相位解缠是InSAR处理的关键环节，解缠相位与目标高程间的关系如式(1)所示：

其中，h为观测目标高程，φ为解缠相位，Hamb为高程模糊度，该参数代表相位每变化 2π所对应的高程变化量，也是衡量InSAR系统的测高灵敏度的重要参考。在不考虑基线、波长等变化引入的空间去相干的前提下，高程模糊度越小，InSAR系统对目标高程变化的感知越敏锐，对应的干涉条纹也将越密集。高程模糊度的计算如式(2)所示：

其中，λ=c/f，λ为雷达系统波长，c为光速，r为斜距，θ为入射角，P代表不同的工作模式，单发双收(双天线)模式下P=1，自发自收(重轨)模式下P=2，B为垂直基线。结合式(1)及式(2)可知，基于系统参数及观测几何信息，通过解缠相位φ即可获取目标高程h。

由式(2)可知，高程模糊度与频率、基线都呈反比，InSAR系统的工作频率越高，或基线越长，对应的高程模糊度越小，越容易获取高精度的高程信息。然而，较高的频率或者较长的基线均会导致空间相干性的降低，加剧相位噪声，导致高程测量误差。所以，传统单通道InSAR常存在高程模糊度与空间相干性间的矛盾。

面向目标高程的有效提取，相位解缠成为In-SAR处理的核心环节。其中，缠绕相位φ与解缠相位φ之间存在如式(3)的关系：

其中，缠绕相位φ在 (-π,π]区间内，k为整数(即为模糊数)。相位解缠的目的即为通过缠绕相位φ求取与高程呈比例关系的解缠相位φ。然而，式(3)中存在k和φ两个未知量，其解并不唯一，故其本质是一个不适定问题(病态问题)。

为实现单通道相位解缠，需采用邻域联合处理，并通过Itoh假设对该问题加以约束，即要求相位满足连续性，相邻像素间的真实相位差需位于(-π,π]区间。在该约束下，相位解缠可通过相邻像素点间的相位梯度积分实现。

然而，在实际地形中，剧烈高程起伏将导致干涉相位无法满足Itoh假设，使得单通道解缠失效。如图1所示，A,B,C为相邻的3个分辨单元，ΔφBA及 ΔφCB分别为B与A、C与B间的真实相位差，ΔφBA及 ΔφCB分别为B与A、C与B间的缠绕相位差，且 ΔφBA=ΔφBA,ΔφCB=ΔφCB。若已获取A点的解缠相位，则基于 ΔφBA(相位差)，通过路径积分方式即可获取B点的解缠相位。但是B,C两点之间的高程存在剧烈的起伏，导致相位欠采样，使得 ΔφCB超过 π。此时通过缠绕相位估计所得的相位梯度 ΔφCB将存在模糊，无法基于路径积分方式获取C点的解缠相位，导致解缠误差积累，并最终引入高程反演误差。因此，传统单通道InSAR相位解缠方法难以适应高程起伏剧烈区域的处理。

图1 相位解缠示意Fig.1 Schematic diagram of phase unwrapping

2.2 多通道相位解缠原理

为解决单通道相位解缠技术在地形剧烈起伏区域的适应性不足的问题，多通道InSAR系统及多通道相位解缠技术应运而生。其中，多通道InSAR有两类主要的实现方式：多频InSAR及多基线InSAR。就系统构建而言，多频InSAR系统需要在单一搭载平台上同时部署两(或多)部频率差较大的SAR载荷(如中国测绘科学研究院的CASMSAR[25]、中国科学院空天信息创新研究院的MSJosSAR[26]等)，且各部载荷需同时工作，使得系统的硬件成本较高，实现也较为困难；而多基线InSAR系统则需在单一搭载平台部署多部SAR天线(如中国科学院空天信息创新研究院的Array InSAR[27]系统、MV3DSAR[28]系统等)，硬件成本将有所降低。此外，多基线InSAR也可通过单部SAR天线的多次重轨观测实现，可通过时间代价进一步压缩硬件成本，成为目前主流的多通道InSAR观测模式。

无论采用多频还是多基线InSAR观测模式，其进行相位解缠处理的本质不变，均是通过频率或基线的改变获取目标区域在不同高程模糊度下的干涉图，借助干涉通道自由度的提升规避相位解缠中的路径积分问题，从而突破Itoh假设的限制，实现稳健的相位解缠。此处以双通道InSAR为例，通过已获取的不同高程模糊度对应的干涉相位，可以给出如式(4)的约束关系：

其中，Hamb1及Hamb2分别为通道1和通道2的高程模糊度，φ1及φ2分别为对应的解缠相位。将式(3)代入式(4)可得

其中，k1及k2分别为通道1和通道2的模糊数。在同一目标点的高程固定不变的前提下，模糊数及其对应的高程解算可视为解“同余方程”的问题，通过CRT算法即可求解[13]。此外，基于干涉相位的概率统计特性同样可推导多通道相位间的约束关系，并由此推出了MLE算法(此处不再赘述)。为了实现相位解缠中的噪声抑制，引入邻域联合处理或先验统计模型的改进算法也被相继推出，如闭合形式的CRT算法[29]、基于线性约束的MLE算法[11]、MAP算法等[12]。

然而，上述处理算法或涉及逐像素估计、逐窗口估计、逐窗口超参数迭代等处理，运算量较大，难以满足大规模干涉图的高效解缠需求。因此，本文考虑使用深度学习结合的方法，在保证精度的同时实现高效的解缠。

3 多通道联合InSAR相位解缠网络：MCJUNet

3.1 网络构建原理

在相位解缠中，用于解缠处理的干涉图呈条纹状形式，干涉条纹(去除平地相位后)的密集程度由地形起伏形式及高程模糊度共同决定。地形起伏越剧烈，高程模糊度越小，对应的干涉条纹越密集，相位解缠也越困难。当干涉条纹过于密集，直至发生相位欠采样时，单通道相位解缠随之失效。

在多通道InSAR处理中，相位解缠可转化为适定问题，其核心是在各通道的相互约束下获取缠绕相位对应的模糊数k，并在此基础上解算解缠相位，从而依据式(1)反演高程。

针对多通道干涉图，其模糊数具有聚类特性，并主要表现为以下特点：每个干涉条纹对应一个模糊周期，该条纹内的所有像素具有相同的模糊数。图2即示意了双通道干涉图及其模糊数的对比。其中，图2(a)对应较大的高程模糊度，图2(b)对应较小的高程模糊度，图2(c)、图2(d)分别对应图2(a)、图2(b)的模糊数。由对比可见，不同高程模糊度的干涉图均呈现聚类现象，但聚类形式存在差异。具有较小高程模糊度(对应高频点或短基线)干涉图的干涉条纹更为密集，解缠相位及对应的模糊数跨度更大，使得模糊数聚类结果中的类别更多。

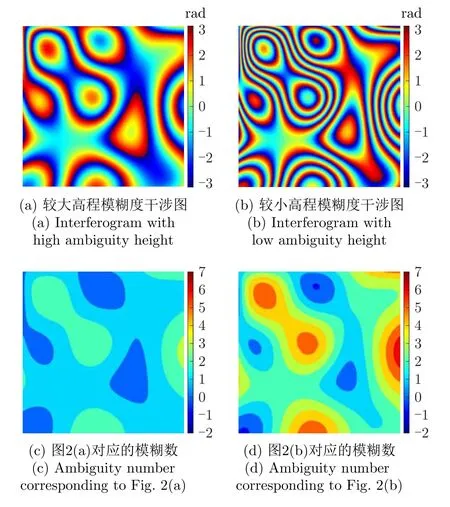
图2 模糊数聚类示意Fig.2 Schematic diagram of the ambiguity number clustering

根据同一干涉条纹中所有像素都对应相同模糊数的特点，可以将模糊数k的求取转化为语义分割问题[30]，即：对应相同模糊数的像素点可归入到同一个像素簇中，将此模糊数的值赋为这个像素簇的语义，根据语义的不同对像素进行分类。在这个过程中，可以采用深度学习方法，将图2(c)、图2(d)作为标签用以训练神经网络，即可利用神经网络完成对干涉图模糊数的语义分割，实现每个像素的模糊数估计，从而获取解缠相位。

3.2 网络总体架构

基于3.1节的分析，相位解缠可转化为语义分割处理。在可用于语义分割的深度神经网络中，UNet网络具有突出的轻量化和高性能优势，可广泛应用于各种场景[31]。所以，本文利用UNet神经网络完成模糊数估计，实现相位解缠。针对UNet神经网络而言，其网络结构呈现为“U”形，可将浅层特征和深层特征紧密融合在一起。其中浅层特征主要用于捕捉图像的边缘轮廓等细节信息，有助于网络学习缠绕相位跳变区域的特征。而深层特征则更专注于表达图像的语义信息，可助力网络学习相位与其邻域像素相位的关系。通过充分融合邻域像素的信息，UNet网络能够准确高效地进行模糊数的估计，从而为大规模干涉相位解缠提供有力支撑。

在多通道相位解缠中，为了获得不同通道缠绕相位所对应的模糊数，此处采用了多输出UNet神经网络，并将所提出的网络命名为MCJ-UNet，用以实现多通道干涉相位的联合处理，并通过改进网络结构及损失函数来保证解缠效果。图3即为双通道解缠网络的结构示意。其中，缠绕相位φn1,φn2以及对应的高程模糊度比例(尺度缩放因子)是网络的输入，经过编码路径和两个解码路径的处理，可完成对两幅干涉图的模糊数估计。

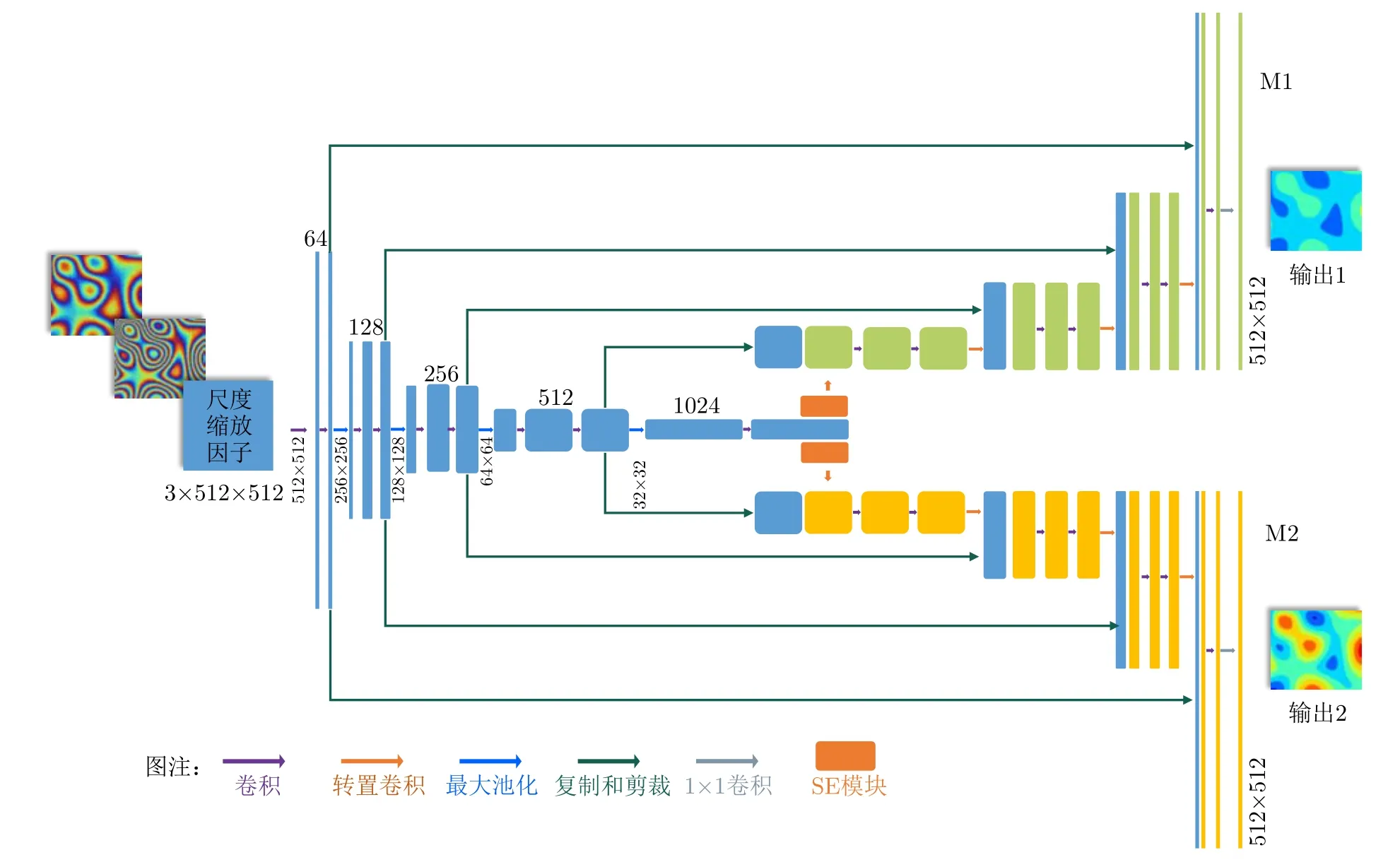
图3 MCJ-UNet网络结构图Fig.3 The structure of MCJ-UNet network

为了描述清晰，此处将网络的输入顺序规定为通道1干涉相位、通道2干涉相位以及尺度缩放因子。通道1的高程模糊度较大(对应短基线或低频点)，而通道2的高程模糊度较小(对应长基线或高频点)，即：Hamb1＞Hamb2。尺度缩放因子(高程模糊度比例)的计算如式(6)，并有α ∈(0,1)。

根据高程模糊度的定义，可以分别得到在多频和多基线观测构型下的尺度缩放因子，如式(7)和式(8)所示：

所构建的MCJ-UNet网络的整体结构如图3所示，该网络采用了两条相同的解码路径，并共享一条编码路径的输出。编码路径主要负责对多通道干涉相位的特征进行提取，由5个子模块组成，由浅入深的逐层提取干涉图的特征信息，每个子模块包括两次卷积和一次池化过程。两条相同构造的解码路径也包括5个子模块，分别为上采样反卷积，全尺度跳跃连接以及两次卷积。

考虑到每条解码路径需要输出不同的模糊数信息，因此需要的特征信息也各有侧重，有鉴于此，在编码路径提取的特征信息和两条解码路径间加入了SE通道注意力模块，旨在增强网络对不同特征通道的感知能力，SE模块的构建原理如图4所示。其核心功能是对每个特征通道进行自适应权重调整，通过学习每个特征通道的重要性来增强可用信息并减弱无关信息。在MCJ-UNet中，编码路径提取到的特征信息同时包含通道1和通道2的干涉相位，而对于各通道的解码路径，SE模块的加入减弱了其他通道的干涉条纹轮廓等信息的权重，使得解码路径可以更加专注于对本通道的模糊数估计所需信息的提取，从而提高模型整体的表现能力。同时，相较于简单的增加网络的深度或宽度，SE不需要大幅增加网络的参数量，可以用较小的计算代价实现更好的性能。

图4 SE模块Fig.4 SE module

3.3 基于多通道联合约束的相位残差损失函数

为了在相位解缠中充分利用不同通道间的干涉相位特性差异，提升信息获取维度，MCJ-UNet对训练过程中的损失函数进行了优化，在损失函数构建中引入了基于多通道联合约束的相位残差项。

图5示意了网络训练过程。将UNet网络用于语义分割任务时，网络输出的特征通道数等于像素分类的类别数。因此，在相位解缠处理中，需要考虑缠绕相位对应的模糊数(类别数)范围，这将决定网络输出通道的数量。对于MCJ-UNet而言，每个解码路径的输出特征通道数与数据集中的模糊数范围相关联。具体来说，假如数据集中所有缠绕相位对应的模糊数满足k1∈(m1,m2),k2∈(n1,n2)，则网络两条解码途径对应的输出特征通道数应分别设置为M=m2-m1+1,N=n2-n1+1，以确保网络能够为每个可能的模糊数提供适当的预测,从而保证模型能够有效地学习和解释不同模糊数对应的缠绕相位信息。

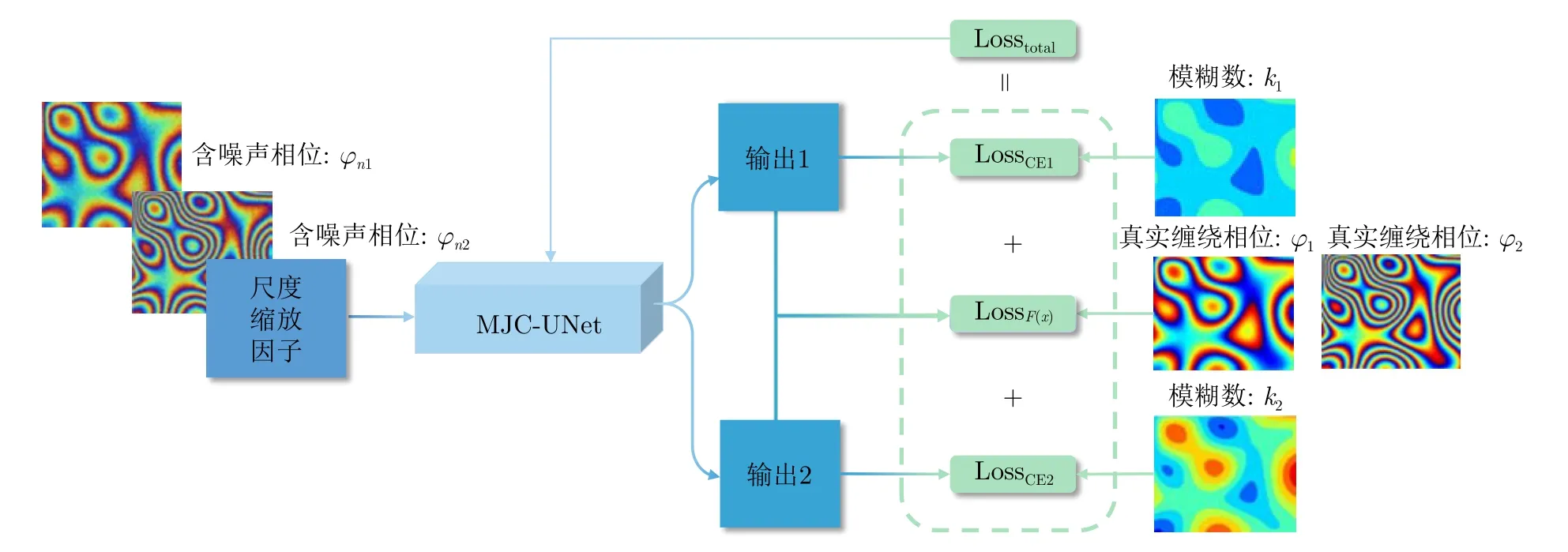
图5 网络训练流程图Fig.5 Flowchart of network training

损失函数对于网络的优化至关重要。在训练MCJ-UNet的过程中，计算损失函数所用的标签包括：多通道相位对应的模糊数k1,k2以及真实缠绕相位φ1,φ2。所用损失函数包括3个部分：LossCE1,LossCE2以 及 LossF(x)。其 中，LossCE1和 LossCE2表示网络两条解码路径的输出与真实模糊数标签之间构成的交叉熵损失[32]，它可以度量模型输出的模糊数概率分布和真实模糊数标签之间的差异。交叉熵损失如式(9)所示：

其中，M为模糊数类别的总数，pi为网络预测输出，表示第i个特征通道对应的模糊数为真实模糊数的概率，yi为符号函数，当像素对应的真实模糊数为第r个类别的模糊数时，有

多通道相位残差优化损失 LossF(x)是根据多通道相位之间的相互约束关系所建立的损失函数，旨在使网络在估计模糊数的过程中结合多通道的相位关系，进行更加准确的模糊数预测。其具体的构成如式(11)所示：

其中，M1和M2为两条解码路径的输出特征通道数，对应于数据集中双通道模糊数的类别数目。pi和pj分别为两条解码路径对每个模糊数的预测概率，k1i为第1条解码路径的第i个特征通道对应的模糊数标签值，k2j为第2条解码路径的第j个特征通道对应的模糊数标签值，φ1,φ2为真实缠绕相位。相位残差F(x)的表达式为

式(11)结合了多通道相位间的相互约束关系与语义分割网络输出不同类别的概率这一特点。在优化网络模型的过程中，该损失函数会首先遍历两个输出特征通道对应的模糊数组合，当遍历到的模糊数组合为真实模糊数时，相位残差F(x)的值会置为0，其他情况下，将相位残差F(x)置为1。因此，为了最小化损失，当遍历到的模糊数组合 (k1,k2)不是(或不全是)真实模糊数时，需要降低相位残差前的概率乘积pi×pj的值，当遍历到模糊数组合为真实模糊数时，需相应提高相位残差前的概率乘积pi×pj。随着相位残差损失 LossF(x)的不断下降，网络会自适应学习多通道相位间的关系，提高真实模糊数的输出概率。

根据3个部分的损失函数，总体损失函数可以表示为

式(13)中的γ和η为超参数，可以通过调整该值来控制每部分损失函数在总体损失函数中所占的比重。由于 LossCE1和 LossCE2对应不同的分类数，且LossF(x)与前两者的计算方法也不同，因此对于同一网络输出的损失函数计算中，每部分损失函数的尺度也不同。因此，需要通过超参数的设置将每部分损失函数的值调整至同一尺度，以均衡各部分损失函数对网络优化的贡献，避免某个损失函数主导整个训练过程。此处给出一种通过预训练来确定超参数的方法，其目的在于通过预训练的方式，观察在模型能够基本完成模糊数预测的情况下各部分损失函数比值。首先仅使用交叉熵损失LossCE1与LossCE2的和作为总体损失函数进行预训练，即预训练过程中损失函数的大小为LossCE1+LossCE2，当网络基本收敛时，计算此时一个训练轮次中三部分损失均值的比值，根据比值确定超参数，使得三部分损失函数可以调整至同一水平。

3.4 基于多通道联合约束的解缠误差自修正

由于MCJ-UNet可同时输出不同通道对应的模糊数，基于单通道模糊数及对应的缠绕相位即可实现相位解缠。在不考虑相干性损失的前提下，高程模糊度越小，理论高程精度越高。因此，在基于所提出的网络完成模糊数的估计后，可选择高程模糊度较小的干涉通道(此处以通道2为例)进行模糊数补偿，从而获取解缠相位

MCJ-UNet的本质为语义分割网络，分割结果中的不同像素簇的语义即为模糊数，分割边缘为相位跳变位置。但是受相位噪声的影响，语义分割边缘难以保证完全精确，该类边缘将出现部分像素的语义估计错误，从而导致相位解缠错误。相位跳变现象主要有两种情况：平缓地形下相位 +π和-π间的跳变和陡峭地形引起的相位欠采样。针对平缓地形区域，相邻像素间的微小高程变化也可能会导致对应的缠绕相位在 +π和 -π间跳变。此时，该相邻像素将对应不同的模糊数(即该像素间将存在语义分割的边缘)，边缘语义分割误差将导致解缠误差。但是，语义分割的边缘由模糊数的分布形式决定，该分布形式由高程模糊度及地形共同决定。由于不同通道间的高程模糊度不同，对应的语义分割边缘将存在差异，即：在某通道存在边缘误差的区域，其他通道极有可能不存在该问题(如图2(c)及图2(d)所示)，因此可以考虑利用这一特性和不同通道间的相位关系对此类误差进行修正。而针对陡峭地形引起的相位跳变现象，可通过多通道相位间是否有差异来判断该跳变是否由地形引入，针对均发生跳变的情况不进行误差自修正的处理，以保证陡峭地形的边缘细节。

针对上述问题，本节提出一种基于多通道联合约束的解缠误差自修正方法。该方法的核心思路为：以参考通道的解缠结果为基准，利用不同通道间的相位关系检测存在解缠误差的像素，并基于不同通道语义分割结果边缘位置的差异，结合其余通道的解缠结果完成修正。由于实际地形中极少出现孤立像素形式的陡峭地形，某像素的解缠相位(或高程)将与邻域若干像素相接近。所以，此处判断是否采信某一通道解缠结果的标准即为解缠相位的邻域梯度，该梯度越小，则表明该像素与邻域像素越相似，其解缠相位的可靠性越高。

该方法的具体操作步骤如下：

步骤1 标记点提取：首先根据式(4)，基于通道1获取的解缠相位以及尺度缩放因子α，可获得对应的通道2的参考解缠相位：

针对该相位差，其理论值应为0(无论是否为陡峭地形)，即表示同一目标的不同通道的解缠结果一致。但实际处理中将受到相位噪声的影响，若该数值较小，则可视为相位滤波等处理过程对某一通道的干涉相位造成细微损失，从而导致双通道解缠结果的微小差异；若该数值较大，则表示某一通道的解缠结果存在误差，需进行误差修正。

此处以阈值φd为参考，标记干涉图中所有|Δφ|＞φd的位置，即可获取所有可能解缠出错的位置，并记为标记点。

步骤2 梯度计算：完成误差标记后，需通过邻域联合处理来判断所采信的通道。此处需计算不同通道的解缠相位中，各个标记点与周围像素点均值之间的梯度，并记作δ1和δ2。

步骤3 误差修正：首先设置替换阈值δd，若同时满足 |δ1|＜δd,|δ2|＜δd，则比较δ1和δ2的 大小，并将 |δ1|＜|δ2|位置上的相位值替换为通道1获取的通道2参考解缠相位φ2cal。当δ1和δ2同时大于替换阈值δd时，视为两个相位梯度都由(陡峭)地形引入，不做替换。

通过上述处理，即可完成基于多通道联合约束的解缠误差自修正。上述描述以双通道为例，当相位解缠扩展到更多通道时，可以选择标记点对应的梯度最小的通道的解缠相位值进行替换，以获取更为准确的解缠相位。

3.5 MCJ-UNet的通道拓展

上述分析均基于双通道相位解缠，此处对MCJUNet解缠推广至多通道进行分析，并假设通道数量为n。

首先，需要对网络模型进行调整，将网络输出通道数与解缠通道数对应，即网络由1条解码路径与n条编码路径构成，每条编码路径负责1个通道的模糊数输出。

其次，需要调整损失函数，多通道解缠网络的总体损失函数由n+1项组成，前n项为n个输出通道的输出与真实模糊数计算所得的交叉熵损失，第n+1项为各通道与参考通道的相位残差损失函数之和。对于各部分损失函数对应超参数的确定，可首先由各通道交叉熵损失函数之和对网络进行预训练，当网络基本达到收敛时，计算一个训练轮次中各部分损失均值的比值，根据该比值即可确定每一部分损失函数对应的超参数的值。

最后，需要对多通道联合约束的解缠误差自修正方法进行调整，即基于参考通道与其他所有通道的解缠相位分别完成标记点提取及梯度计算，并以梯度最小的通道为参考完成误差修正，获取多通道联合解缠相位。

将MCJ-UNet中的双通道相位解缠推广至多通道时，网络模型将增大，对应的损失函数计算量也将增加，使得网络训练需要耗费更长的时间。但是更多的通道数会为网络提供更多的特征信息进行学习，且多通道的解缠信息也有助于多通道联合约束下的解缠误差自修正处理，以保证相位解缠的精度。

4 数据集构建

为了对所提出的MCJ-UNet网络进行训练，此处尽可能模拟不同类型的复杂地形[33]，并构建了对应的多通道干涉图及标签数据。图6-图8示意了数据集的构造过程，具体步骤如下：

图6 仿真地形构造示意Fig.6 Schematic diagram of simulated terrain construction

(a) 构建初始随机地形：首先创建一个尺寸为L×L的初始矩阵，并对每个位置随机赋高度值，其中L ∈[3,25]，如图6(a)所示。随后，将初始矩阵插值扩展到 512×512，完成初始地形的构造，如图6(b)所示。其中初始矩阵的边长L的大小可以控制地形的复杂程度，L越大则构造的地形越复杂。

(b) 增添地形纹理：为了尽可能模拟真实地形，可在步骤(a)生成的光滑仿真地形上增添不规则的纹理。纹理的构造方式和地形构造类似，区别在于将初始矩阵的边长L增大至 256×384的尺寸，但所赋高度值将降低，生成纹理后可将其增添到所构造的地形上。

(c) 生成多通道干涉图：首先设置大小随机的两个高程模糊度Hamb1＞Hamb2，并计算尺度缩放因子α。基于随机生成的高程模糊度及所构建的地形高程，可获取绝对相位，将绝对相位缠绕至(-π,π]，即得到多通道干涉图，如图7(b)及图7(e)(其局部放大图如图7(c)及图7(f))所示，细节纹理的添加可使得训练数据更接近实际地形下所获取的干涉图。

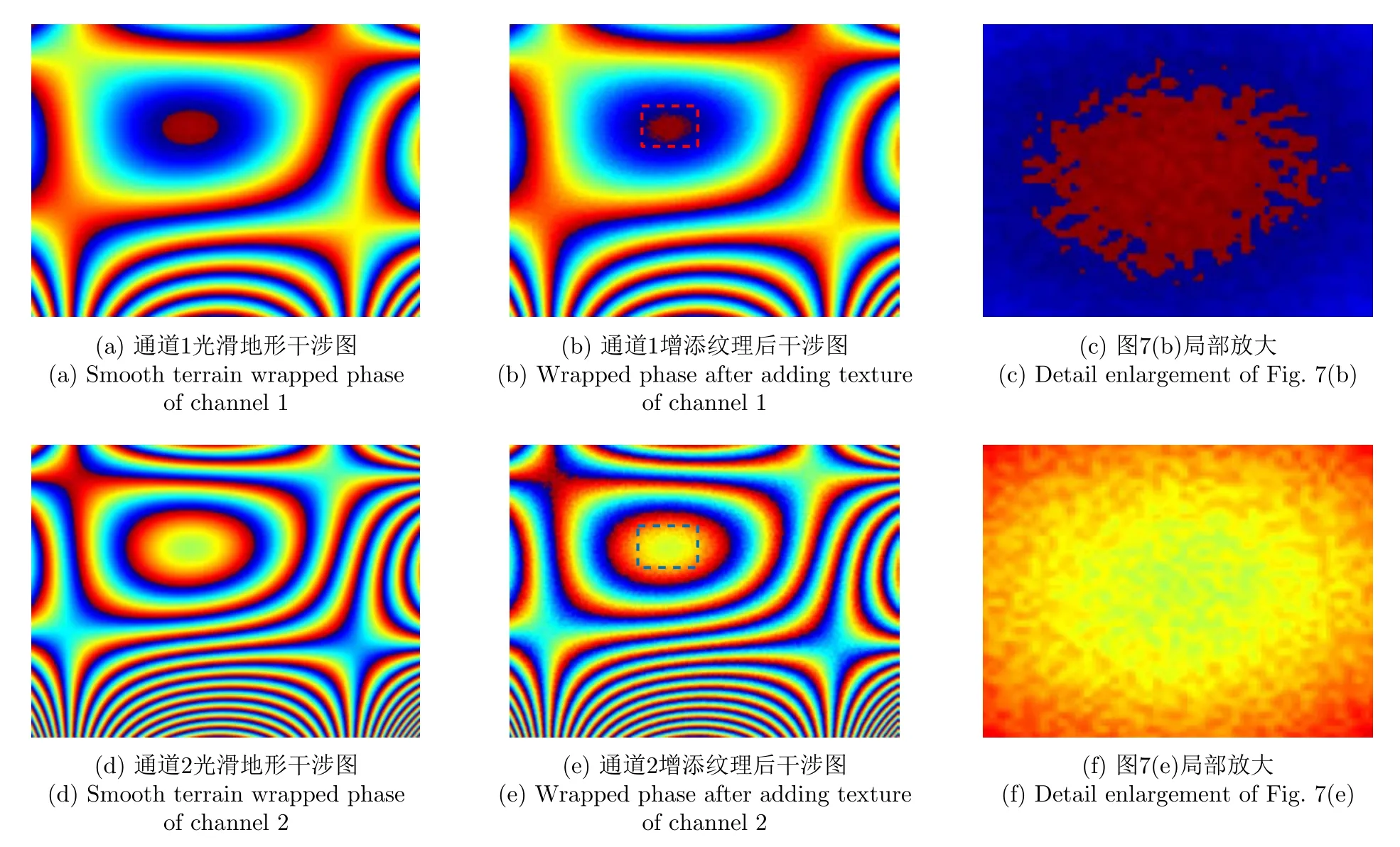
图7 增添纹理前后缠绕相位对比Fig.7 Comparison of wrapped phase before and after adding texture

(d) 完成数据集构造：为尽可能模拟实际情况下所获取的干涉相位，对获取的缠绕相位增加随机强度的高斯复噪声，添加的相位噪声信噪比均匀分布在-1～10 dB，添加噪声后的干涉图如图8(a)及图8(b)所示，该图即可作为网络输入，每幅干涉图对应的模糊数作为网络标签，如图8(c)及图8(d)所示。

图8 多通道缠绕相位及标签Fig.8 Multi-channel wrapped phase and label

为突出网络多通道相位解缠的优势，在数据集的构建过程中还增加了一些陡峭地形，以形成相位欠采样数据：在步骤(a)中，可选择初始矩阵的一部分数据进行插值扩展，另一部分不做插值只做扩展，后续步骤则不变。未做插值的部分将生成陡峭地形，供MCJ-UNet学习相位欠采样情况下的多通道相位特性。

5 实验与分析

为验证所提出的MCJ-UNet网络的有效性，此处分别开展了模拟地形仿真验证、真实地形仿真验证以及实测数据验证。其中，模拟地形同时包含平缓及陡峭地形，以验证所提MCJ-UNet在自然及人工场景下的解缠效果；真实地形仿真实验采用了多频(多基线)相位解缠实验中常用的陡峭山地数据：Isolation峰地形数据，以验证所提MCJ-UNet在真实陡峭地形下的解缠效果；实测数据验证选用了TerraSAR-X重轨多基线干涉数据，该数据的尺寸较大，以验证所提出的MCJ-UNet的相位解缠效率。

5.1 网络设置

所提出的MCJ-UNet基于Pytorch 1.13.0及Python 3.9搭建，在NVIDIA Tesla A100 GPU上实现，GPU数量为2。网络共包含2个干涉通道，干涉通道1的输出特征通道数目设置为15，干涉通道2的输出特征通道数目设置为25。训练数据集采用第4节所述方法生成，共包含9000组训练数据及1000组测试数据。训练过程中，使用Adam优化算法[34]进行损失函数最小化，采用余弦退火学习策略[35]，学习率最大值为10-4，最小值为10-6，batch size设置为8，训练轮次为50次。网络预训练用时9587.39 s，根据预训练结果将超参数设置为γ=0.8,η=0.1，网络训练耗时15236.20 s。

5.2 模拟地形仿真验证

模拟地形仿真实验采用双频InSAR构型，主要仿真参数如表1所示，两个干涉通道的频点分别为5.25 GHz及11.50 GHz，对应的尺度缩放因子为0.46。仿真所采用的DEM如图9(a)所示，并在此基础上增添了纹理细节，以逼近真实地形。模拟地形中同时包含平缓(左侧)及陡峭(右侧)区域，陡峭区域的边缘已出现相位欠采样问题。

表1 模拟地形仿真参数Tab.1 Simulation parameters of simulated terrain

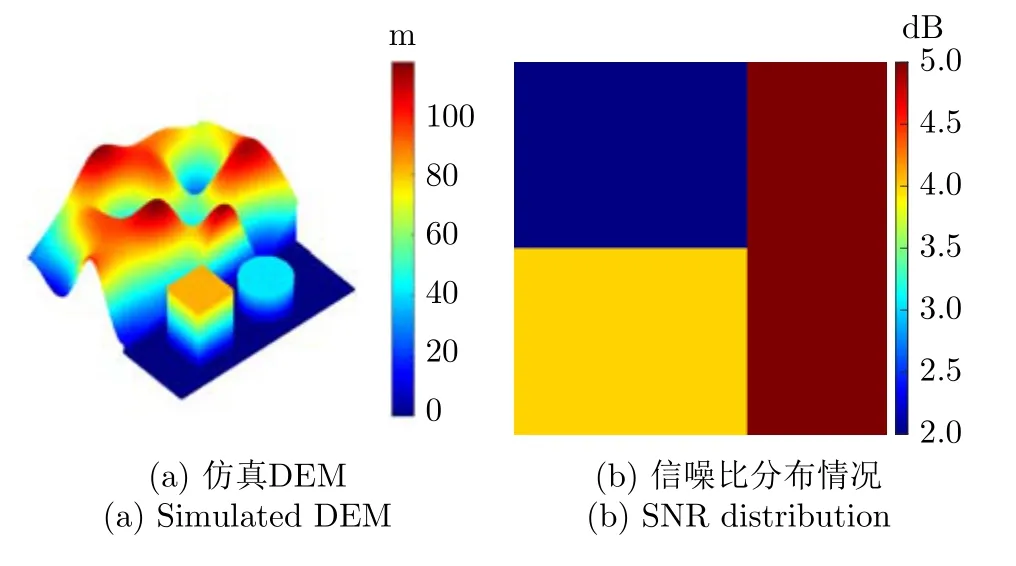
图9 仿真DEM及信噪比分布情况Fig.9 Simulated DEM and SNR distribution

根据仿真DEM所生成的频点1、频点2的参考解缠相位如图10(a)、图10(b)所示，生成的含噪声干涉图如图11(a)、图11(b)所示，其中所添加的信噪比随相位空间分布的不同而变化，平缓(左侧)区域上半部分添加噪声信噪比为2 dB，下半部分添加噪声信噪比为4 dB，陡峭(右侧)区域添加噪声信噪比(Signal-to-Noise Ratio,SNR)为5 dB，如图9(b)所示。

图10 双频点参考相位

图11 双频点(含噪声)干涉图Fig.11 The interferograms of dual-frequency channels

首先，将滤波前的双频点干涉图及对应的尺度缩放因子输入训练完成的MCJ-UNet，所获得模糊数估计结果如图12(a)、图12(b)所示。之后，利用模糊数估计结果及滤波后干涉图可获取双通道相位解缠结果，如图12(c)、图12(d)所示。最后，基于多通道联合约束的解缠误差自修正方法，即可获取MCJ-UNet最终解缠结果。其余实验的MCJ-UNet结果均根据上述步骤获取，将不再赘述。其中，网络的输入采用的是滤波前的干涉图，这是由于在网络训练阶段已输入不同水平噪声的干涉图作为训练数据，神经网络已经学习噪声特征，使用滤波前的含噪声干涉图不会影响网络的预测结果，反而可以尽量避免滤波处理对细节特征的损失，以保证网络的输出提供更细致的地形信息，便于解缠处理。

图12 基于MCJ-UNet所获取的模糊数估计结果Fig.12 Ambiguity number estimation results obtained based on MCJ-UNet

为了对比验证所提出的MCJ-UNet的相位解缠效率及噪声抑制效果，分别采用4种不同方法进行了处理，包括：传统MLE算法、TSPA算法、CANet算法以及所提MCJ-UNet算法。在所涉及的针对干涉图滤波的处理中，4种处理方法均采用Goldstein滤波算法[36]，并在随后的实验中保持一致。为维持噪声水平的一致性，同一组实验选用相同大小的滤波参数。

4种方法的解缠结果如图13所示，其中图13(b)、图13(d)、图13(f)、图13(h)分别为图13(a)、图13(c)、图13(e)、图13(g)相对于高频点参考解缠相位(图10(b))的解缠误差。为了进行定量比较，表2列出了各解缠结果的主要评估指标：解缠相位均方根误差(Root Mean Squared Error,RMSE)以及运行时间。其中，RMSE评估中的参考数据为仿真DEM对应的参考解缠相位，运行时间分为网络运行时间及后处理所用时间，由于MLE和TSPA方法不涉及网络处理，其后处理时间即为处理总时间(下述实验相同)。

表2 各方法所获取的仿真地形解缠相位评估结果Tab.2 Evaluation results of the unwrapped phase of simulated terrain obtained by different methods

图13 仿真数据各方法解缠结果对比Fig.13 Comparison of results for different methods on simulated data

由图13(b)可见，MLE算法由于噪声抑制能力有限，解缠结果中存在明显的相位跳变，出现了大量解缠误差，且由于添加噪声随空间分布不同，解缠结果左侧上半部分出现误差的像素点明显多于下半部分。基于TSPA获取的解缠结果在图中右下角正方形中出现了整体区域的解缠错误，这是由于TSPA方法在第一阶段需要计算相邻像素相位的梯度，而由于滤波原因导致此区域边缘原有梯度信息遭到破坏，错误的梯度信息将正方形区域“包围”。路径积分处理会导致误差的积累，从而使得TSPA在该区域的解缠出现误差。基于CANet和MCJ-UNet的方法均有效完成了干涉图解缠，不同空间分布的噪声并未造成解缠失效问题。且解缠误差主要位于仿真地形的边缘区域(如平缓与陡峭地形交界处)，该误差主要由滤波处理导致的细节损失引入。

表2所示4种方法的RMSE也与上述分析相符，TSPA由于部分区域的解缠失败，因此解缠误差较大，CANet和MCJ-UNet解缠精度相近，验证了两种方法在不同强度和不同空间分布的噪声下的有效性。CANet的网络处理时间及解缠精度略优于MCJUNet，而得益于更简单的后处理步骤，MCJ-UNet的总体运行时间要优于CANet，在保证解缠精度的同时也具有高效性。

5.3 真实地形仿真实验

真实地形仿真实验采用美国Colorado州Isolation山峰区域的真实高程进行，其地形变化形式较为复杂，是多频、多基线相位解缠算法验证中较为经典的实验数据[18,22]，可以有效验证所提方法在自然陡峭地形下的解缠效果。仿真参数如表3所示，真实地形参考高程如图14(a)所示，图14(b)、图14(c)为根据仿真参数生成的含噪声双频干涉图，图14(d)、图14(e)为对应的滤波结果。图15(a)为频点2对应的参考解缠相位，图15(b)、图15(c)、图15(d)、图15(e)分别对应MLE,TSPA,CANet及MCJ-UNet这4种方法的解缠结果，图15(f)、图15(g)、图15(h)、图15(i)展示了4种方法解缠结果相对于参考相位的解缠误差。表4列出了各方法解缠精度和处理时间的评估结果，以进行定量比较。

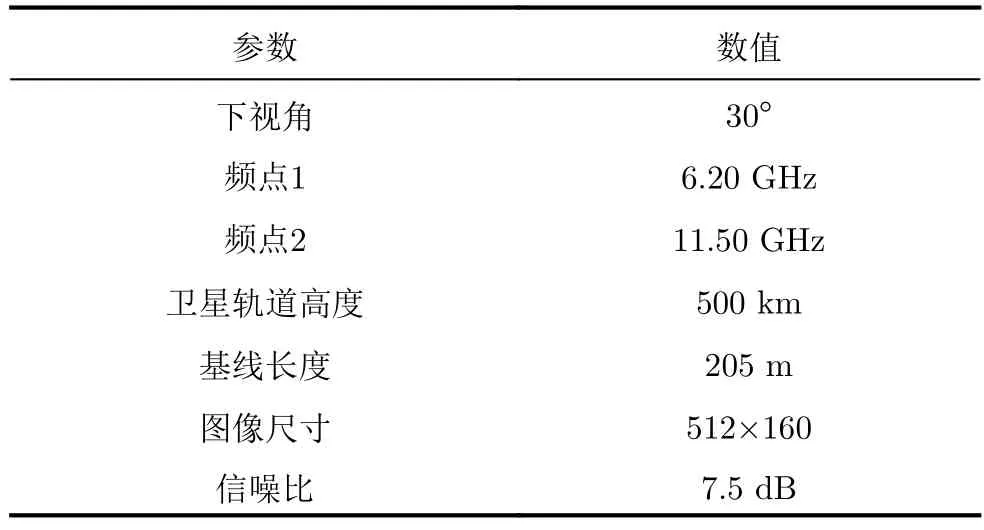
表3 真实地形仿真参数Tab.3 Simulation parameters of real terrain

表4 各方法所获取真实地形仿真相位解缠评估结果Tab.4 Evaluation results of real terrain simulation phase unwrapping obtained by different methods

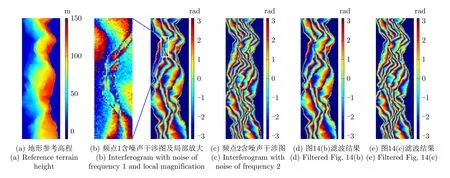
图14 地形参考高程及多频干涉图Fig.14 Reference terrain height and multi-frequency interferograms

图15 参考相位及各方法解缠结果对比Fig.15 Reference phase and comparison of unwrapped phase obtained by different methods

由图15以及表4对比可知，基于逐像素处理的MLE方法噪声鲁棒性较差，解缠精度较低。基于TSPA方法和CANet方法获取的解缠结果在图中上部的陡峭区域均出现错误。针对本文所提出的MCJUNet方法，其单通道(通道1及通道2)的解缠精度均低于CANet方法，这是由于单通道解缠结果未进行误差自修正处理，模糊数跳变区域的部分边缘像素的分类误差导致解缠错误。此外，精度评估采用通道2的参考解缠相位，由于通道1的高程模糊度较大，相比于通道2，其解缠相位经尺度缩放后对应的解缠误差也越明显，故解缠精度略低。虽然MCJUNet的单通道解缠结果精度低于CANet方法，但是在进行多通道联合解缠误差自修正后，其解缠精度明显提升，已略优于CANet的解缠精度。

对上述处理结果进行详细分析可知，在陡峭地形区域的左侧，频点1的含噪声干涉图中可见相位跳变现象(如图14(b)白框及其局部放大所示)。由于MCJ-UNet采用滤波前的干涉图作为网络输入，并且引入跳跃连接的U-Net神经网络对此类轮廓信息较为敏感，因此在该区域内部获得了正确的模糊数估计结果，仅在边缘跳变区域出现了解缠误差。TSPA和CANet方法均采用滤波后干涉图作为输入，并涉及梯度积分处理，存在误差积累及细节损失。MCJ-UNet在陡峭边缘区域的误差是由于频点1和频点2的模糊数在该边缘同时发生跳变，当边缘位置的某些像素处的双通道解缠相位均存在误差时，所提出的解缠误差自修正方法难以判别准确的解缠相位，部分像素的解缠误差无法被有效修正。

对于真实地形下的仿真实验，表4的评估结果显示，MCJ-UNet的解缠精度优于其他3种方法，且处理时间较低。MCJ-UNet方法在真实地形仿真实验与模拟地形仿真实验的运行时间并未与像素点的数量呈正比，这是由于网络运行时间包含了模型加载时间，当干涉图尺寸较小时，模型加载时间在网络运行时间的占比较高，干涉图尺寸的影响不明显。当MCJ-UNet用于更大规模干涉图的相位解缠时，模型加载时间所占网络运行时间比重将降低，处理时间将有所增加，但其解缠高效性的优势将进一步突出。

5.4 实测数据验证

实测数据验证采用TerraSAR-X重轨多基线数据，观测区域为中国山西太原东北部的系舟山山区。该区域属于太行山脉中段分支，地形起伏明显，可以充分验证所提方法在实际处理中的应用效果。数据尺寸为4096×4096，覆盖面积达到7 km×8 km，可有效评估所提方法在大尺寸干涉图上的解缠效率。该数据主要参数如表5所示，图16(a)为目标区域SAR图像，图16(b)为该区域的光学图像。图16(e)、图16(f)分别为双基线原始干涉图，图16(g)、图16(h)为对应的去平地并滤波后的干涉图，两幅干涉图对应的全图平均相干系数分别为0.62(基线1)和0.58(基线2)，图16(d)即为基线2对应的相干系数图。图16(c)为基线2对应的该区域参考解缠相位，该相位以ALOS-DEM[37]高程数据为参考获取，其网格尺寸为12.5 m，高程精度可达3～9 m[38]，可以为不同方法的解缠精度评估提供有效参考。此外，通过该高程数据计算得到的该区域的最大地形坡度接近50°，属于较陡峭地形。

表5 多基线InSAR实测数据主要参数Tab.5 Main parameters of multi-baseline InSAR real data

图16 多基线InSAR实测数据Fig.16 Real InSAR data of multi-baseline

实测数据验证采用前文所述4种方法进行比较，图17(a)-图17(d)对应4种方法的解缠结果，图17(e)-图17(h)为4种解缠结果相对于目标区域参考相位(图16(c))的解缠误差，表6展示了各方法解缠结果的评估指标。

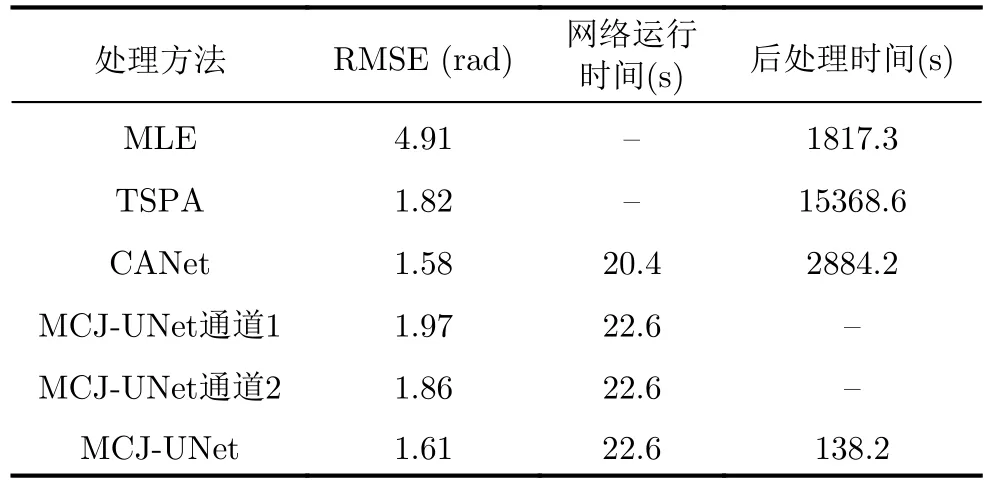
表6 各方法所获取实测数据解缠相位评估结果Tab.6 Evaluation results of unwrapped phase of real data obtained by different methods

图17 实测数据各方法解缠结果对比Fig.17 Comparison of unwrapped phase obtained by different methods for real data

由于噪声抑制能力有限，基于MLE方法获取的解缠结果存在大量散点误差。基于TSPA方法获取的解缠结果在图像右上角相干性较低且地形变化较为复杂的区域出现部分解缠错误，且由于干涉图尺寸较大，TSPA解缠处理的时间成本明显高于其他3种方法。CANet方法和本文所提MCJ-UNet方法解缠结果均未出现大面积误差，解缠精度相当。MCJ-UNet的解缠误差主要位于双基线干涉图模糊数跳变边缘重合的位置，此处在进行多通道联合解缠误差自修正后仍存在少量像素的误差残留。但是，MCJ-UNet的双通道相位解缠精度相比于单通道具有明显提升，验证了基于不同通道的模糊数分类边缘的差异进行解缠误差自修正的处理方法的有效性。此外，与5.3节的分析结论一致，由于精度评估采用通道2的解缠相位为参考，通道1的基线长度较短，对应的高程模糊度较大，所以在经过尺度缩放后，其相比通道2的解缠精度更低。

在针对解缠效率的详细对比中，虽然CANet与MCJ-UNet的网络运行时间相当，但MCJ-UNet的后处理时间具有明显优势，处理时间不足CANet后处理时间的5%，有效降低了大规模干涉图解缠的时间成本。因此虽然MCJ-UNet解缠方法在解缠精度上和CANet方法相当，但是在处理效率方面表现更为突出，这意味着大规模干涉图解缠或对实时性要求较高的场景下，MCJ-UNet方法将更具优势。

6 消融实验

为验证所提网络优化方法以及相位残差损失函数的有效性，本节进行了消融实验，对比在相同训练条件下(如5.1节所述)，各种方法在测试集上的模糊数分类准确率以及相应的训练时间。对比方法分为网络结构有无SE模块以及损失函数有无多通道相位残差项，实验结果如表7所示，其中，方法4为本文所提方法。由表7数据可知，4种方法中通道1的模糊数分类准确率要优于通道2，这是由于通道1的分类数少于通道2，相应的分类难度较为简单。对比方法1和方法3以及方法2和方法4，SE模块的加入略微增加了网络的训练时间，但显著提升了各通道模糊数的分类准确率，证明了其在网络优化过程中的有效性。对比方法1和方法2以及方法3和方法4，多通道相位残差优化损失的加入提高了网络分类的准确率，同时对通道2的提升更加明显，使得不同通道的分类准确率差距变小，证明了相位残差损失结合多通道相位关系的有效性。由于损失函数计算量的增加，网络训练时长也相应增加，但是不会增加网络结构的复杂度，也不会影响网络处理时间，因此相较于准确率的提升，此处的网络训练时间的增加在可接受的范围内。

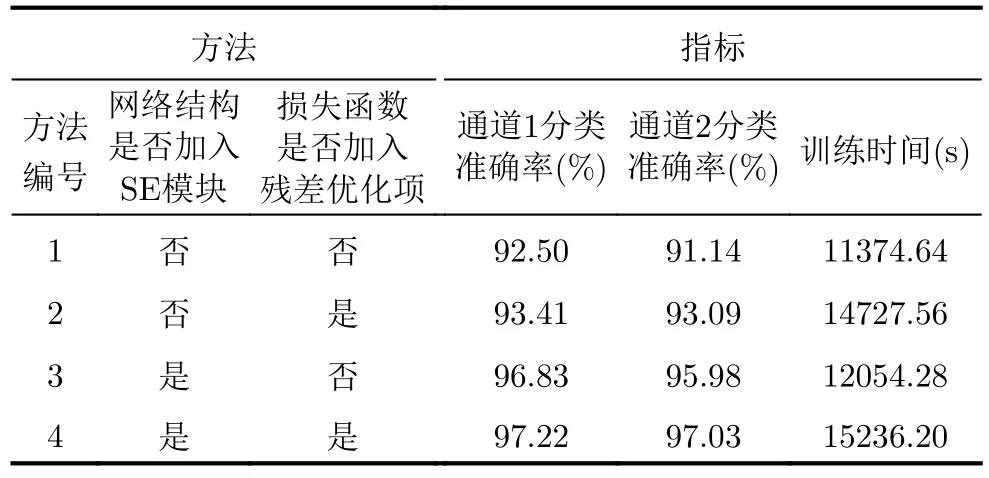
表7 各对比方法的分类准确率及训练时间Tab.7 Classification accuracy and training time of each comparison method

7 结语

面向InSAR相位解缠技术的高效应用，本文提出一种基于深度学习的多通道联合相位解缠网络：MCJ-UNet。该方法结合了多通道相位解缠思路和神经网络模型，将相位解缠中的模糊数估计问题转化为了语义分割问题，采用多输出UNet完成处理。在网络优化过程中，该方法引入了SE模块以增强不同输出通道对所需特征信息的感知能力，并引入了多基线相位残差损失以增强网络对多基线干涉相位间约束关系的学习。此外，为进一步抑制相位解缠误差，该方法引入了基于多通道联合约束的解缠误差自修正处理，借助不同通道间的模糊数分类边缘的差异进行解缠误差的检测及修正，实现了各通道解缠相位的有效融合，保证了相位解缠质量。

基于所提出的MCJ-UNet方法完成了模拟地形仿真、真实地形仿真及TerraSAR-X实测数据验证。实验结果表明，MCJ-UNet可有效实现多通道联合相位解缠，在平缓及陡峭地形下均具有较强的适用性。就解缠精度而言，该方法优于MLE方法和TSPA方法，与同为基于深度学习的多通道相位解缠的方法CANet的精度相当。就解缠效率而言，由于采用直接估计模糊数的解缠方式，该方法的处理效率具有明显优势，将更适用于大尺寸干涉图的解缠处理，也为基于深度学习的相位解缠提供了一种新的思路。

此处需要说明的是，由于网络化处理中需要进行卷积操作，所输入的数据尺寸需为32的倍数，针对于尺寸非32整数倍的数据，可以在边缘进行补0操作。对于极大尺寸的数据(如数据尺寸超出处理平台的并行处理能力)，也可通过分割处理进行分别解缠。另外，需要注意的是，在网络训练过程中，需要数据集的模糊数分类范围涵盖解缠数据对应的范围，所以在训练时需要尽量生成较大模糊数区间的数据，或依据特定数据的模糊数范围选择对应区间的网络进行处理，以保证解缠网络的适用性。

未来的研究将继续拓展所提出的网络模型，以适应更为复杂的观测地形，并聚焦强噪声环境下的相位滤波处理，构建基于深度学习网络的相位滤波及相位解缠一体化处理框架，以支撑InSAR技术的大规模高效应用。

利益冲突所有作者均声明不存在利益冲突

Conflict of InterestsThe authors declare that there is no conflict of interests