合成孔径雷达快速后向投影算法综述

邢孟道 马鹏辉 楼屹杉 孙光才 林 浩

①(西安电子科技大学雷达信号处理全国重点实验室 西安 710071)

②(西安电子科技大学前沿交叉研究院 西安 710071)

1 引言

现如今，合成孔径雷达(Synthetic Aperture Radar,SAR)[1]技术向着低约束飞行轨迹、多成像模式、宽测绘带等方向发展，这对成像算法的通用性提出了更高的要求。传统频域算法[2-7]更多依赖于对斜距历程的建模，随着SAR系统飞行轨迹越发复杂，斜距历程多变，同时回波信号存在更为严重的二维耦合空变问题，使得频域算法存在较多限制[8,9]。相较之下，由计算机层析领域引入的后向投影(Back Projection,BP)算法[10-14]，通过在时域逐脉冲相干积累能量得到精确聚焦的图像，可以认为无限制，几乎能够满足所有的成像模式。但其运算效率十分低下，在实际工作中难以应用，因此针对BP算法的研究主要集中在解决其加速问题。自1999年Yegulalp[15]提出快速后投影(Fast Back Projection,FBP)算法和2003年Ulander等人[16]提出快速多级后投影(Fast Factorized Back Projection,FFBP)算法后，研究人员开始了对快速BP算法的探索，提出了众多的基于不同成像面坐标系的快速BP算法，主要可以分为基于距离-方位平面坐标系、地平面坐标系和非欧氏坐标系的3类快速BP算法。

距离-方位平面坐标系主要适用于最基本，也是最常见的直线平飞轨迹，该轨迹的斜距历程始终在同一平面内变化。因此，在距离-方位平面上建立坐标系，复杂程度低，更易于成像。基于该成像面坐标系的快速BP算法，在距离-方位平面中建立成像网格得到低分辨率子孔径图像，然后通过对低分辨率子孔径图像升采样相干融合得到最终成像结果。相比于距离-方位平面坐标系，地平面坐标系主要应用于机动轨迹。考虑到雷达轨迹在三维空间中复杂多变，成像平面随运动轨迹而变化，距离-方位平面与地平面间的投影为非线性变化[17]。因此，基于距离-方位平面坐标系的快速BP算法无法直接应用。针对机动轨迹下平台运动特性和实际成像需求，基于地平面坐标系的快速BP算法在地平面建立坐标系，并布置成像网格。不同于前两者，非欧氏坐标系大多见于高轨SAR系统中。需要指出的是，高轨SAR系统长时间持续观测和超大幅宽引入的二维相位误差会导致图像散焦[18-20]。因此非欧氏坐标系在地平面坐标系成像的基础上考虑地表弯曲的影响，基于此成像面坐标系的快速BP算法在地平面建立贴合实际地面的曲面成像网格。此外对于快速BP算法，其关键之一在于成像面内不同坐标系的选取，主流坐标系种类主要有极坐标系与直角坐标系。目前最具有代表性的快速BP算法是FFBP算法[16]，它基于波束锐化的思想，在局部极坐标系下进行成像，然后对各子孔径图像进行相干融合，最后合成成像结果。FFBP算法虽然极大提高了成像效率，但在各级子孔径图像融合时需要进行插值处理，影响了成像质量。而对于直角坐标系下快速BP成像，虽然在图像相干融合时只需简单的平移相加，无需插值处理，但受限于高采样率需求，容易造成频谱混叠，因此对于各类成像面直角坐标系快速BP算法的研究依旧是个挑战。

与此同时，对于机动平台SAR而言，其通常运行在对流层中，受大气湍流和其他气象因素的影响较大[21]，导致航线可能偏离理想的轨迹，从而产生运动误差，并且使得SAR回波信号的相干性减弱，影响SAR成像质量，甚至出现散焦现象。因此针对机动平台SAR开展与快速BP算法相结合的运动补偿技术研究至关重要。

综上所述，快速BP算法实现有效减少计算量的核心在于选取合适的坐标系。不同平台具有各自的运动特征，快速BP算法选取的坐标系有所差异。因此，本文针对基于不同成像面坐标系的快速BP算法，首先简要介绍了原始BP的原理，对各类成像坐标系进行比较，并对极坐标系与直角坐标系之间的频谱进行分析。然后对基于距离-方位平面坐标系、地平面坐标系和非欧氏坐标系的3类快速BP算法进行了阐述，重点介绍了作者团队近年来在快速BP算法方面开展的研究工作。最后对全文进行总结，并展望未来快速BP成像算法的发展趋势。

2 快速BP基础概述

2.1 原始BP和快速BP算法原理

BP成像作为一种无近似的成像算法，可以应用于任意运行轨迹与任意成像模式。其成像步骤可简化为：首先建立成像网格，然后计算网格中每个点的相干积累结果[22]。BP成像几何模型如图1所示，图中紫色线条为雷达的飞行轨迹，虚线为雷达运动轨迹在地面的投影，地面蓝色网格为成像网格。假设场景中存在一点p，对其在方位时间ta收到的回波信号经过距离脉压后可表示为

图1 任意模式下BP成像几何模型Fig.1 BP imaging geometry model in arbitrary mode

其中，tr为距离快时间，Krc=4πfc/c 为中心波数，fc为载频，c为光速，B为发射带宽，Rp(ta)为点目标p到雷达相位中心的斜距，sinc(tr)=sin(πtr)/(πtr)。

BP成像算法将每次脉冲回波数据经脉冲压缩后投影回成像场景，能量在合成孔径时间内相干积累，得到全分辨率的图像，能量相干积累公式如下所示[8,9,23]：

其中，I(x,y) 表示BP的成像结果，ts和te为合成孔径时间的起止时间。从式(2)可以看出BP成像只需取每个方位时刻ta的回波信号，并补偿对应的相位信息，最后进行累加就可以计算出 (x,y)处的图像值。但是由于BP算法在成像过程中需要对每个点在每个脉冲时刻与SAR平台的瞬时距离都要进行精确计算，并以此通过插值在回波中提取相应的能量，大量的逐点插值操作使得BP算法的计算量庞大。例如假设合成孔径时间内有N次脉冲，那么生成一幅N×N的图像总共需要进行N3次插值，计算效率低下成为影响BP发展与应用的重要限制。

为了解决BP算法的计算效率低下的问题，近几年来提出了各类快速BP算法，其发展脉络如图2所示。由于BP算法的计算量与回波数据的长度和图像的大小呈正相关，因此早期的快速BP算法原理是将回波数据进行子孔径划分，在每个子孔径上分别进行低分辨率成像，最后进行子孔径图像相干融合，使得计算效率得到大幅提升。但需要注意的是，在子孔径相干融合提升分辨率时，其计算量要小于子孔径高分辨率成像时所需的计算量。在后续众多学者对快速BP算法的研究中，发现能够实现加速的前提是低分辨率子孔径图像频谱没有混叠，子孔径成像需要满足Nyquist采样需求，而不同坐标系的采样率需求不一样。在极坐标系下能以较低的采样率对图像进行采样，且不会造成频谱混叠。但是图像在极坐标系下会发生畸变，不同极坐标之间的畸变不一样，在图像相干融合时需要进行插值处理。而直角坐标系对二维空域进行均匀采样，图像融合时直接相干索引叠加即可，但其高采样率会使得计算效率大幅降低。

图2 快速BP算法发展脉络图Fig.2 Fast BP algorithm development venography

因此，对于成像坐标系的选取，在不同成像面内进行快速BP成像具有重要作用。

2.2 成像坐标系

对于各类快速BP成像算法，其中一个关键问题是选择一个合适的坐标系，使子孔径BP图像的频谱可以在相对较窄的范围内压缩。目前已有的坐标系种类主要有极坐标系、直角坐标系和鉴于两者之间的虚拟极坐标系。又可以根据低分辨率子孔径图像所在坐标系与最终全分辨图像所在坐标系是否一致分为局部坐标系和全局坐标系。

Yegulalp等人提出的FBP和Ulander等人提出的FFBP算法，都是基于局部极坐标系来实现对原始BP算法的加速。如图3所示，以每个子孔径中心为原点分别建立局部极坐标系 (r,θ)，其可以分为距离维与角度维。当角度维的网格划分较为稀疏时，可以充分发挥局部极坐标系在角度维低采样率的特点，只需较少的采样点便可以重建低角度维分辨率的子图像，这就是这类算法运算效率相较于原始BP算法得以大幅提升的关键。通过在局部极坐标系下进行子孔径图像逐级相干融合来提高成像分辨率，但多次插值操作会造成误差积累，使得成像效果较差。

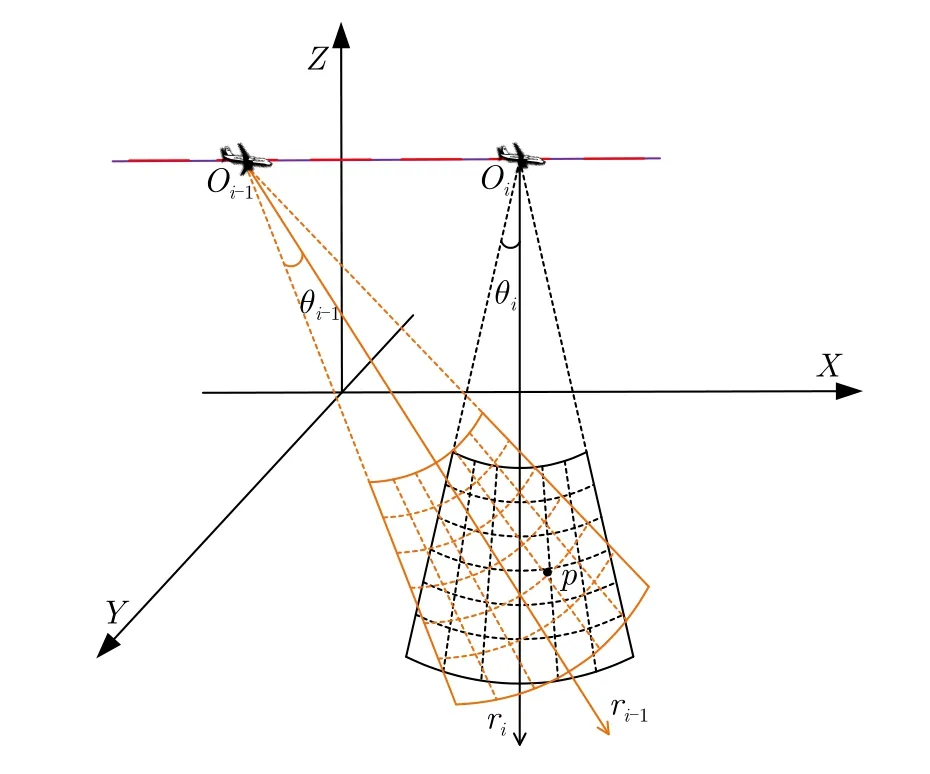
图3 局部极坐标系Fig.3 Local polar coordinates system

在低分辨率子孔径图像融合和极坐标系图像转换为最终直角坐标系图像的过程中，需要在距离维与角度维进行插值处理。大量的插值操作使得计算效率与成像质量恶化，因此如果减少插值的计算负载就能极大提高算法效率与成像质量。Zhang等人[24,25]提出了一种如图4所示的以全孔径中心为原点的全局虚拟极坐标系 (r,sinθ)。子孔径成像采用全局虚拟极坐标系，使得所有子孔径图像的波数谱均位于统一波数空间，只需对子图像的波数谱进行方位平移，便可实现波数谱融合，不需要进行插值，因此避免了插值误差和对波数谱的破坏，能够精确地保留波数谱的原有形式。但其要求子图像波数谱无模糊，且最后仍需要利用二维插值操作将图像从极坐标系转换到直角坐标系，使得计算量增加。

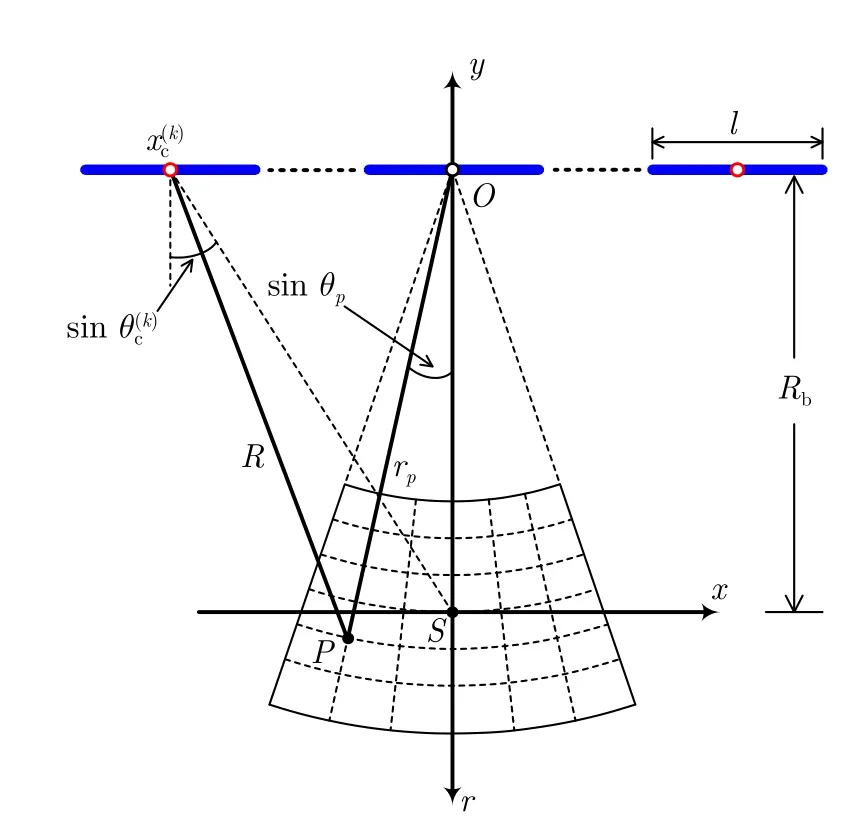
图4 全局虚拟极坐标系Fig.4 Global pseudo polar coordinate system

虽然在全局虚拟极坐标系下成像时，可以很好地避免插值操作所带来的误差积累，但在超高分辨率需求条件下时，难以满足成像需求。文献[26]中提出了一种混合坐标系。如图5所示为混合坐标系成像网格划分，以子孔径中心为原点，y轴垂直于雷达飞行方向。对成像场景按距离维与角度维平均分割，建立新的成像网格 (y,θ)，其中y是场景内像素到飞行轨迹的最近距离，θ是像素点到原点的连线与y轴的夹角，r为像素点到原点的距离，三者的关系为y=r·cosθ。与极坐标相比，混合坐标系成像系统不需要在距离维进行插值，只需在角度维上进行插值，减少了插值计算，从而提高了运算效率。但由于图像相干融合时依旧存在插值操作，图像质量也就不可避免地会受到影响。

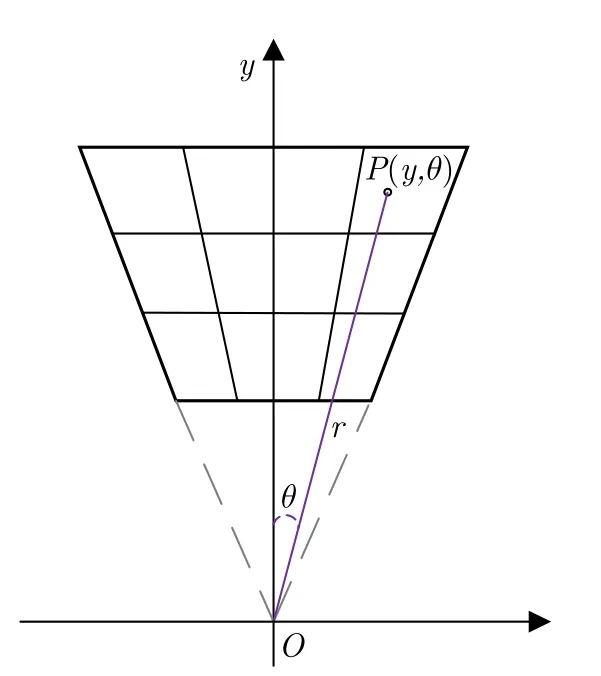
图5 混合坐标系Fig.5 Hybrid coordinate system

相较于上述各类坐标系，直角坐标系有几何构型更简单、编程实现更容易等优势。并且当在直角坐标系下进行波束形成时，只需要简单的平移操作即可完成图像投影，而如果应用于聚束模式，更是无需任何操作，直接相干索引叠加即可。然而直角坐标系下过高的采样率需求使得运算效率低下，并且会造成频谱混叠。为了突破在直角坐标系下的子孔径成像需要高采样率的限制，西安电子科技大学提出了基于全局直角坐标系下的多平台各类快速BP成像算法，在图像相干积累的过程中充分利用直角坐标系无需插值与逐点运算的优势。以全孔径中心在地面上的投影为原点，建立如图6所示全局直角坐标系，虽然仍采用子孔径进行成像然后融合，但不同于极坐标下的成像算法，每一级的子孔径采用同一个直角坐标系进行成像。且由于所布置的成像网格在整个方位向上为均匀分布，不同子孔径所对应的网格区间是已知可求的，因此在低分辨率子孔径图像融合时，不再需要逐点运算与插值融合，直接进行相干索引叠加即可。同时，随着合成孔径时间的增加，子孔径的成像网格间距逐渐缩短，方位分辨率也将提升。

图6 全局直角坐标系Fig.6 Global cartesian coordinate system

对上述所提的对各类坐标系进行比较，如表1所示。在极坐标下进行的快速BP成像算法，能以较低的采样率进行子孔径低分辨率成像，但由于其为局部坐标系，各级图像相干融合时需要进行插值操作，会导致误差积累，影响成像质量。而由极坐标系衍生出的虚拟坐标系，虽然可以采用全局坐标系的优势，不再需要进行插值处理，但限制条件较大，难以普及。而在混合坐标系进行快速BP成像时，虽然相较于局部极坐标系下成像，减少了插值次数，但依旧会有误差积累，影响成像质量。相较于极坐标系下的各类快速BP算法，直角坐标系下成像质量更高，并且在全局直角坐标系下，整个低分辨率子孔径图像融合过程中可以充分利用直角坐标系平移不变特性，更利于工程化实现。但为了突破直角坐标系对低分辨率子孔径图像采样率的限制，需要充分分析图像频谱，探寻造成采样率过高的原因。

表1 各类坐标系下成像优缺点对比Tab.1 Comparison of advantages and disadvantages of imaging in various coordinate systems

2.3 极坐标系与直角坐标系下的频谱分析

无论已有的局部极坐标系快速BP算法还是全局直角坐标系快速BP算法，都是通过把回波数据进行子孔径划分处理来减少计算量。而对于每个子孔径，仅需要进行低分辨成像，就可以带来计算效率的大幅提升。因此，子孔径图像的分辨率决定了快速BP算法的计算效率。然而，为了保证子孔径图像能够有效通过相干合成来提升分辨率，子孔径图像的分辨率需要满足目标频谱采样需求。对于较窄的频谱带宽，只需较低的采样率就可以满足BP映射的要求，而且不会造成模糊。

由于角度维所需的采样率较低，因此在极坐标系下可以大幅压缩信号采样率而不会造成频谱混叠，极坐标系也就成了FBP与FFBP的首选。并且，Yegulalp在文献[15]中给出了局部极坐标系下二维波数谱的支撑区为

其中，Vmax和Vmin为频率最大值与最小值，l为子孔径长度。根据Nyquist采样定理，局部极坐标系下距离维与角度维的采样需求为[16]

其中，λmin为最短波长。可以发现距离维采样率需求仅与发射带宽相关，而角度维的采样需求与子孔径长度相关。通过仿真实验对FFBP算法成像过程中的一个子孔径成像结果进行分析，来验证上述结论。成像结果如图7所示，可以发现在FFBP算法中，子孔径实现全分辨率成像只需较窄的频谱宽度，也就是较低的采样率即可满足成像要求。

图7 FFBP成像仿真Fig.7 FFBP imaging simulation

下面分析在直角坐标系下的频谱特性。通过对全局直角坐标系下SAR二维波数域进行分析，得到波数谱的二维支撑区分别为[9,27]

其中，θmax和θmin为斜视角的最大与最小值。根据Nyquist采样定理，对子孔径成像网格采样的要求为

在聚束模式下时，θmax-θmin可以看作波束宽度与合成孔径角之和。对于较短子孔径的成像结果，尽管子孔径合成孔径角较小，但较宽的波束决定了图像仍需要较高的采样率。而y方向的采样率则由带宽所决定。同样通过仿真实验对直角坐标系下子孔径BP成像进行验证，其成像分辨率与上述极坐标下的FFBP算法分辨率相同，成像结果如图8所示。对比两者仿真结果，可以发现直角坐标系下子孔径成像频谱宽度明显大于极坐标系下子孔径图像频谱宽度，需要更高的采样率来满足成像需求，但较高的采样率会带来成像网格点数的增加和额外的运算负担。

图8 直角坐标系BP成像仿真Fig.8 Cartesian coordinate system BP imaging simulation

在极坐标系下进行快速BP成像，可以利用其采样率有大量冗余这一特性，通过粗糙图像逐级合成来提高成像效率，但在图像相干融合过程中，由于存在不同极坐标系间的投影，需要进行大量插值处理，对成像质量有影响。而直角坐标系，虽然其在图像融合过程中有巨大的优势，图像相干积累只需要简单的平移操作即可[27]。但由于其高采样率需求，无法通过孔径分割逐级合成来提高计算效率。为了使得子孔径在直角坐标系下成像时可以满足低采样率需求，对图8成像结果进行一次频谱压缩，结果如图9所示。可以发现此时频谱宽度已明显变窄，但对频谱进行放大后，可以发现依旧存在频谱展宽现象，需要进行进一步的频谱压缩处理。而对于不同成像面直角坐标系，其成像时所需的频谱压缩操作也不同。因此，本文基于不同成像面直角坐标系下的频谱特性，对适用于各自成像面直角坐标系下的频谱压缩技术进行详细介绍。

图9 频谱压缩结果Fig.9 Results of spectrum compression

3 基于距离-方位平面坐标系的快速BP成像

随着技术发展，基本模式下SAR成像难以满足应用需求。以BP算法为代表的时域算法，由于具有适用于任意模式、任意轨迹的优势，其在SAR成像领域受到广泛关注。目前针对原始BP算法计算效率低下而衍生出的快速BP算法，其大都是在雷达飞行方向与波束方向所在的距离-方位平面上建立各类坐标系，从而布置相应的成像网格，其成像模型如图10所示。该模式主要适用于沿直线轨迹飞行的机载SAR成像，或者其他平飞模式下的SAR成像。本节基于距离-方位平面坐标系模型，对各类坐标系下快速BP算法进行描述，并针对直角坐标系对子孔径高采样率的限制，详细描述了直角坐标系下的频谱压缩技术。

图10 距离-方位平面坐标系成像模型Fig.10 Imaging model in the distance-azimuth plane coordinate system

3.1 距离-方位平面极坐标系快速BP算法

由于极坐标系下低采样率需求，极坐标系在快速BP算法中应用广泛，而FFBP算法是极坐标系下最经典的快速BP成像算法。

在初始阶段，FFBP算法将全孔径划分为若干个子孔径，并以各子孔径中心为原点，在各自局部极坐标系内生成一幅低分辨率子图像。在处理阶段采用逐级叠加的方法，将多个子孔径图像进行相干融合，得到新一级更高分辨率的子孔径图像，并随着递归融合的进行，子孔径的长度不断增加，子孔径的数目不断减少。最后，将极坐标图像变换到直角坐标系，得到全分辨率的图像。对于场景中的点目标，在不同子孔径坐标系下，其子图像具有不同的距离和角度坐标。因此，在融合不同孔径对应的子图像时，需要进行原坐标系到新坐标系的映射。目前，这个映射过程主要依赖于距离域和角度域的插值操作。插值操作主要包括两个步骤：首先，计算待插值像素点在投影斜距和投影视角方面的信息；其次，通过升采样或者截断的加权sinc插值方法来计算待插值像素点对应的数值。然而，每次相干叠加前的插值操作都会使得误差积累，影响成像质量，分级次数越多，误差积累越严重。因此，在第1步划分子孔径时，通常采用较长的子孔径，便于减少误差积累。同时，文献[24]提到FFBP算法中所划分的第1级子孔径不能过小，其计算效率随着分级次数增加而提升。这是由于FFBP算法第1阶段采用BP积分进行波束形成，而第1级子孔径越长，分级次数越少，其运算效率就会越低。综上所述，FFBP算法的精度与效率难以两全。尽管通过提高升采样率和增加sinc插值核的点数，以及减少FFBP算法的递归次数，可以在一定程度上改善插值精度并减少插值误差的累积，但这些方法仍然无法完全避免插值误差，而且可能会增加运算负担。因此，实际操作中往往牺牲FFBP的计算效率以获得较好的聚焦效果，因此FFBP的计算效率也难以达到理论值使用一组机载聚束SAR实测数据对FFBP算法进行验证，其实测成像结果如图11所示，成像效果较为良好。

图11 FFBP算法成像结果Fig.11 The imaging result of FFBP algorithm

针对FFBP算法存在的缺陷，文献[28]尝试通过优化参数设置和选择插值核来改善FFBP算法的性能，但并未从根本上消除插值误差的问题。文献[29]使用极坐标格式算法替换FFBP算法初始阶段中低效的BP成像，相较于FFBP算法，该算法中图像融合的迭代次数减少，运算效率与成像质量同时得到提高，但在后期图像融合过程中依旧需要进行插值处理。文献[30]提出了基于坐标系转换的FFBP快速实现方法，通过平移和线性变标操作取代插值操作，但依旧需要在极坐标系下进行图像融合操作。由于在斜视超带宽模式下进行FFBP成像时，即使很短的子孔径也会导致相对较大的频谱带宽，文献[31]提出了基于虚拟极坐标的改进FFBP算法，不同于传统FFBP算法，其将子孔径回波数据递归映射到虚拟极坐标系下，将SAR图像的频谱压缩到较窄的范围内，可以充分利用快速BP图像低采样率的特点，提高计算效率。文献[32]提出一种改进的基于方位等距坐标的FFBP算法，可以在不影响图像质量的情况下实现成像效率的提高，但是当成像网格的方位方向与回波数据方位分辨率方向不一致时，该方法受到限制而无法应用。

文献[24]提出了一种适用于高分辨聚束SAR成像的加速后向投影(Accelerated Fast Back Projection,AFBP)算法。与FFBP算法使用递归插值实现图像融合的方式不同，AFBP算法由于采用全局极坐标系重建子孔径图像，所有子图像波数谱均位于同一波数空间，因此只需对子图像的波数谱进行方位平移，便可实现波数谱融合，再通过二维傅里叶逆变换实现图像聚焦。AFBP算法不需要进行插值，因此避免了插值误差和对波数谱的破坏，能够精确地保留波数谱的原有形式，这使得AFBP算法在效率和精度方面都比FFBP算法更好。但该算法要求子图像波数谱无模糊，且最后需要将图像从极坐标系变换到直角坐标系，增加了计算量。使用X-波段高分辨率聚束SAR实测数据对AFBP算法性能进行验证，成像结果如图12所示。通过观察子场景成像结果，可以发现聚焦后的点目标突出，聚焦效果良好，有效地避免了插值误差对图像质量的影响。

图12 文献[24]所提算法成像结果Fig.12 The imaging result of the proposed algorithm in Ref.[24]

3.2 距离-方位平面直角坐标系快速BP算法

不同于极坐标系，直角坐标系受限于高采样率需求，容易造成频谱混叠。

为了突破在直角坐标系下子孔径成像要求高采样率的限制，文献[27]提出一种在直角坐标系下进行波束形成的快速BP算法，称为直角坐标多级后投影(Cartesian Factorized Back Projection,CFBP)成像算法，其流程图如图13所示。首先建立二维平面直角坐标系，在直角坐标系下进行低分辨的子孔径BP成像，然后通过频谱压缩和补零上采样提升子孔径图像的分辨率，最终只需要简单地将子孔径图像相加就可以得到全分辨的图像。在整个子孔径合成过程中只需要采用快速傅里叶变换(Fast Fourier Transform,FFT)操作，相比于FFBP算法不仅降低了算法的计算量，而且更利于工程化实现。

图13 文献[27]所提算法流程图Fig.13 Flow chart of algorithm proposed in Ref.[27]

文献[27]通过对第i个像素点 (xi,yi)的斜距进行泰勒展开，发现展开项中的二次项是导致频谱展宽的原因，并构建与之对应的谱压缩函数：

其中，距离波数K拆分为Kc+Kr,-B/2≤Kr≤B/2 。使用Fc1和Fc2进行频谱压缩后，方位频谱宽度表示为

在经过Fc1和Fc2补偿后，此时与极坐标系下的图像融合相似，由于直角坐标系成像后带宽与孔径长度成正比，因此通过划分长度较短的子孔径，在大幅度降低子孔径采样率的同时，可以保证频谱无模糊。然后进行直角坐标系下的图像相干积累处理，由于不再需要进行插值操作，相较于FFBP算法，计算效率得到提升。

采用一组机载聚束SAR实测数据对CFBP算法进行验证，并与FFBP算法成像进行比较，其成像结果如图14。FFBP算法成像结果中可以观察到目标存在散焦，较CFBP成像结果散焦更严重，旁瓣更高，质量更差。并且在耗时上，FFBP算法耗时3815 s，而CFBP算法仅耗时713 s，其计算效率更快。

图14 FFBP算法与文献[27]所提算法结果对比Fig.14 The FFBP algorithm is compared with the results of the proposed algorithm in Ref.[27]

对FFBP算法与CFBP算法的计算量进行分析对比。假设方位采样为La，生成图像大小为N×N像素点，子孔径数量为n，原始BP成像采用8倍插值处理，计算量如表2所示，其中FFBP算法采用了8倍sinc插值核进行二维插值。当N=16384，子孔径数量n=32时，CFBP算法与FFBP算法计算量随方位采样点数的变化如图15所示，可以发现CFBP算法计算量小于FFBP算法。

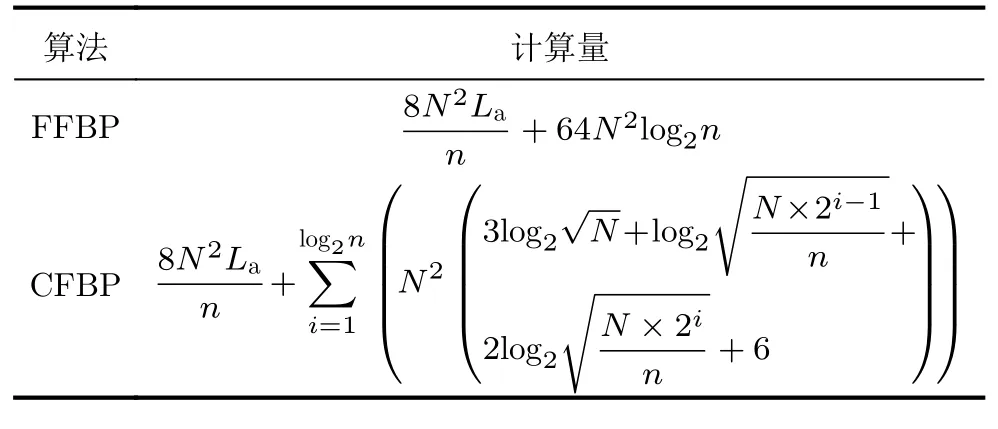
表2 FFBP算法与CFBP算法计算量对比Tab.2 Comparison of computational burden between FFBP algorithm and CFBP algorithm

图15 FFBP算法与CFBP算法计算量对比Fig.15 Comparison of computational load between FFBP algorithm and CFBP algorithm

相较于传统基于极坐标系的FFBP,CFBP无需逐点插值，避免了因插值处理而导致计算效率和计算精度之间的矛盾[9,27]。

4 基于地平面坐标系的快速BP算法

随着雷达搭载平台的多样化发展，平台运行轨迹变得多样化与复杂化。在距离-方位平面坐标系进行快速BP成像时，由于距离-方位平面与地面之间的投影为线性变化(即模型中雷达运动轨迹较为单一)，难以满足复杂机动轨迹下SAR成像需求。对于如图16所示的灵活飞行轨迹SAR、弹载SAR以及圆周轨迹SAR等各种灵活机动轨迹，其成像平面随着飞行轨迹变化，没有统一的斜距平面，难以同时兼顾算法的成像效率与实时性。本节主要描述基于地平面坐标系的快速BP算法，在地面上建立坐标系与布置成像网格，以满足复杂机动轨迹下对地面实时精确成像需求。

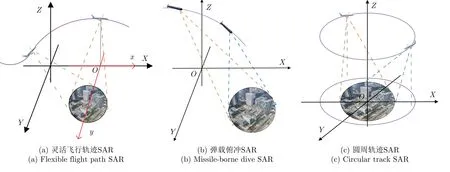
图16 地平面坐标系成像模型Fig.16 Imaging model in ground plane coordinate system

4.1 地平面极坐标系快速BP算法

对于极坐标下的FBP与FFBP算法，虽然都是在原有BP算法的基础上进行改进，提高计算效率，但FFBP算法的多级运算处理不适合进行并行运算。为此，在条件允许的情况下，一般采用更适合并行运算的FBP算法[33]。由于后期图像处理中用来特征匹配的SAR图像，其分辨率不需要很高，因此在投影操作时，只需使用临近点插值进行能量积累即可，剩余计算主要集中于斜距计算上。为进一步提升BP算法成像效率，文献[34]从斜距历程形式出发，提出了一种基于FBP算法进行场景划分的快速BP算法，该方法将全孔径与全场景划分为若干子孔径与子场景，对相同子场景中的像素点进行距离徙动近似，避免了FBP算法在计算斜距时需逐点计算的问题，进一步提升效率。

FFBP算法虽然无法进行并行运算，但可通过拆分BP积分，逐级合成同样使得BP算法效率大幅提升。文献[16]给出的计算量分析表明，FFBP算法的成像效率与频域算法可以达到相同的水平，并且文献中FFBP算法考虑了方位方差的变化和地形的变化，与直接返回投影相比，其计算效率得到显著提升。文献[35]基于子孔径处理技术，提出一种适用于弹载双基前视SAR成像的扩展FFBP算法，在椭圆极坐标系下进行子图像处理，并对子图像进行不同的Nyquist采样，使得计算效率得以提升。文献[26]对传统极坐标网格进行改进，提出基于混合坐标系的快速BP算法，将距离维与角度维平均分割，建立混合坐标系成像网格。在子孔径图像从极坐标转换为直角坐标时，只需对角度维插值即可，不再需要对距离维插值，减少了子孔径图像融合过程中的插值误差与计算量。该算法成像结果如图17所示，其成像质量良好。

图17 文献[26]所提算法成像结果Fig.17 The imaging result of the proposed algorithm in Ref.[26]

4.2 地平面直角坐标系快速BP算法

在地平面上布置直角坐标系进行成像处理时，文献[36]提出基于局部直角坐标系和子区域处理的频域BP算法，在距离-多普勒域进行相干积分，实现方位聚焦。其流程图如图18所示，主要分为5个步骤，首先统一进行距离徙动校正与加速度补偿，然后通过方位谱滤波来划分子区域并进行子区域距离徙动校正，然后通过频域后向投影与子区域图像拼接得到最终成像结果。该算法通过建立局部直角坐标系的斜距模型，使得近似误差更小，子区域具有相同处理架构，因此不需要进行子块拼接，避免了频域子孔径方法存在方位不连续的问题。但其没有考虑子区域加速度所引起的空变剩余相位和剩余距离徙动，适用范围受到限制。其实测结果如图19所示。

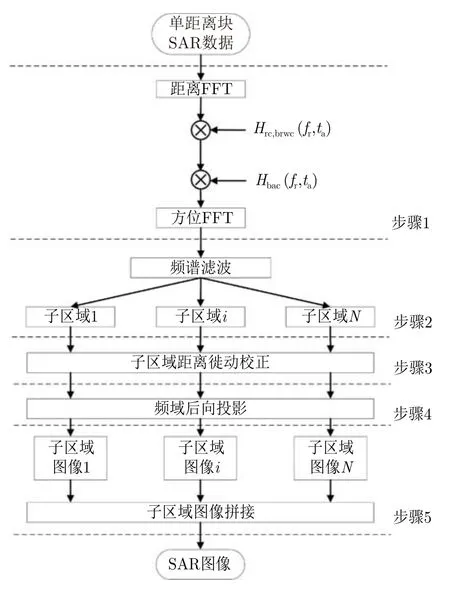
图18 文献[36]所提算法流程图Fig.18 Flow chart of algorithm proposed in Ref.[36]

图19 文献[36]所提算法成像结果Fig.19 The imaging result of the proposed algorithm in Ref.[36]

对于全局直角坐标系下的CFBP算法，因为在求解谱压缩函数时多次使用了近似处理，CFBP算法受到极大限制，只能对正侧视小范围的距离-方位平面进行成像。对于复杂多变的俯冲轨迹，由于其成像模式多样，成像平面随着飞行轨迹变化，没有统一的斜距平面，无法满足其变斜距的成像精度要求。针对这一问题，Chen等人[37]提出了一种基于地平面直角坐标系的快速BP (Ground Cartesian Back Projection,GCBP)算法，在地面布置直角坐标系成像网格，通过采用两步谱压缩技术实现子孔径图像的频谱压缩。其主要流程与各步骤计算量如图20所示。该算法考虑三维机动轨迹在地平面建立直角坐标网格，能够适用于任意轨迹、任意前斜角和任意成像模式。采用两步谱压缩，突破成像对图像采样率要求过高的限制，实现无需插值的快速BP成像，同时GCBP算法适用于分块并行处理，并且满足实时成像的要求。目前，该技术已成功应用于某型号导引头上。

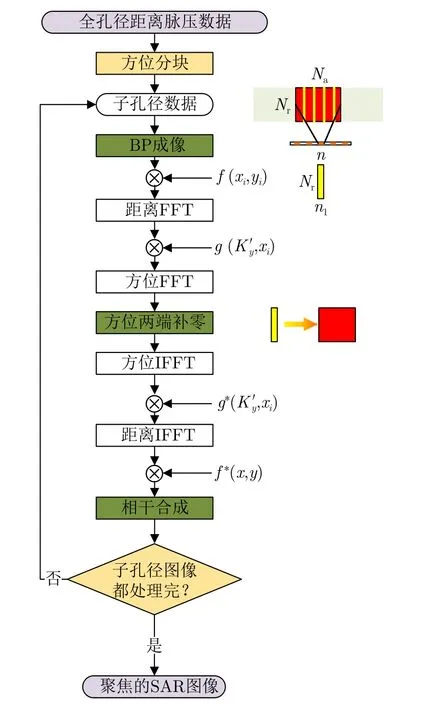
图20 文献[37]所提算法流程图Fig.20 Flow chart of algorithm proposed in Ref.[37]

因为波数的变化是连续的，并且子孔径时间较短，因此可以假设目标的谱中心 (Kxc,Kyc)由子孔径中心时刻ti决定，因此通过波数分解后目标点的频谱表达式可以写为

其中，(Xi(ti),Yi(ti),Zi(ti)) 表示雷达在ti时刻的位置，Krc为载频对应的发射波数。

GCBP算法第1步和第2步，需要分别建立全孔径和子孔径的成像网格和坐标系。第1步谱压缩通过对子孔径图像I(xi,yi)补偿一个二维相位函数f(xi,yi)实现，即：

此时，目标的频谱移动到了频谱中心，而经过第2步谱压缩后，频谱倾斜将会得到矫正。频谱倾斜矫正是以频谱中心线为基准，也就是移动频谱中心线的位置来实现频谱矫正。在距离频域矫正沿水平向空变的谱倾斜时，采用相同的方法补偿相位，即第2步谱压缩函数：

其中，yc为yi的中心值。图21显示了局部BP图像波数支持区域的示意图。可以直观地看出，经过第1步谱压缩后，空变的谱中心偏移被消除，在第2步谱压缩后，空变的频谱倾斜也被消除。

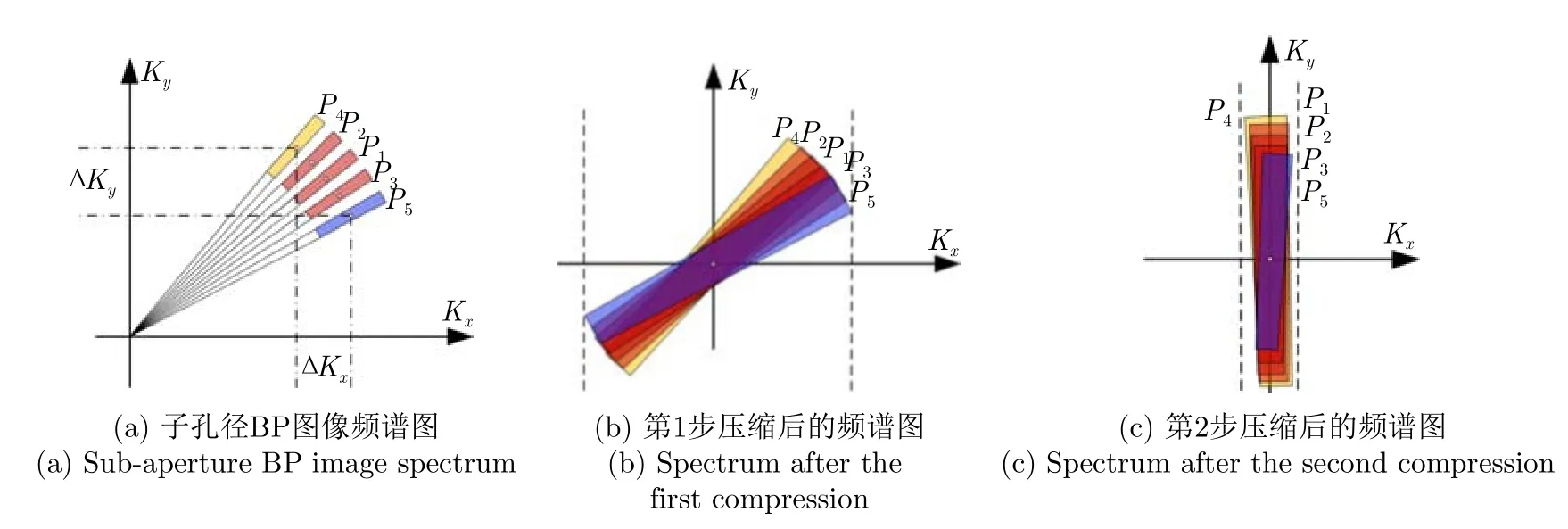
图21 文献[37]所提谱压缩示意图Fig.21 The schematic diagram of spectrum compression proposed in Ref.[37]

使用两组机载SAR实测数据对GCBP算法进行分析验证，其图像结果分别如图22(a)、图22(b)所示，对于图22(a)的计算时间，在同一台单处理器上工作时，原始BP算法需要消耗125 min来构建最终图像，而GCBP算法仅需9 min。观察成像结果，可以发现两组数据都聚焦良好，证明GCBP算法对俯冲模式下具有良好的成像效果且效率更高。假设方位采样为La，图像最终大小为N×N，子孔径数量为n，采用8倍插值处理。文献[26]、文献[36]与文献[37]所提算法的计算量如表3所示。当N=16384，子孔径数量n=32时，三者计算量随方位采样数变化如图23所示。GCBP算法计算量略高于角度维采用8倍插值的文献[26]所提算法，低于文献[36]所提算法。

表3 文献[26]、文献[36]与文献[37]所提算法计算量对比Tab.3 Comparison of computational burden between algorithm Proposed in Ref.[26],Ref.[36] and Ref.[37]

图22 文献[37]所提算法成像结果Fig.22 The imaging results of the proposed algorithm in Ref.[37]

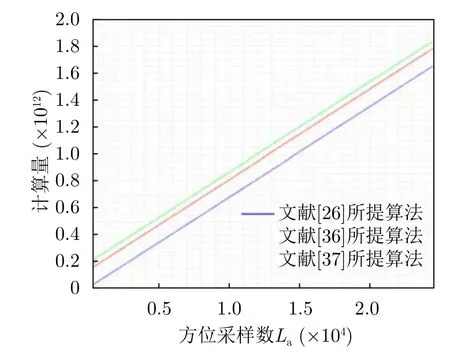
图23 文献[26]、文献[36]与文献[37]所提算法的计算量对比Fig.23 Comparison of computational load between the proposed algorithm in Ref.[26],Ref.[36] and Ref.[37]

5 基于非欧氏坐标系的快速BP成像

前文所述的距离-方位平面坐标系与地平面坐标系主要应用于低空轨道，此时地面观测场景相较于雷达而言可以认为是平面几何，也就是欧氏几何。对于高轨SAR成像，其具有超大的宽测绘带以及优秀的续航能力[38-40]。但由于运行高度在几百公里到几万公里不等，此时雷达与地表具有巨大的高度差异，使得地表弯曲不可忽略。如图24所示，高轨SAR对地成像时，地面观测场景为曲面几何，也就是非欧氏几何，如图中红色观测区域所示。而基于平面坐标系的快速BP算法主要适用于低空SAR成像场景，即观测场景中的弯曲幅度可以忽略不计，而对于高轨SAR成像不再适用。因此，如何在非欧氏几何空间内设置坐标系，从而布置成像网格，对高轨SAR快速BP算法研究具有重要意义。

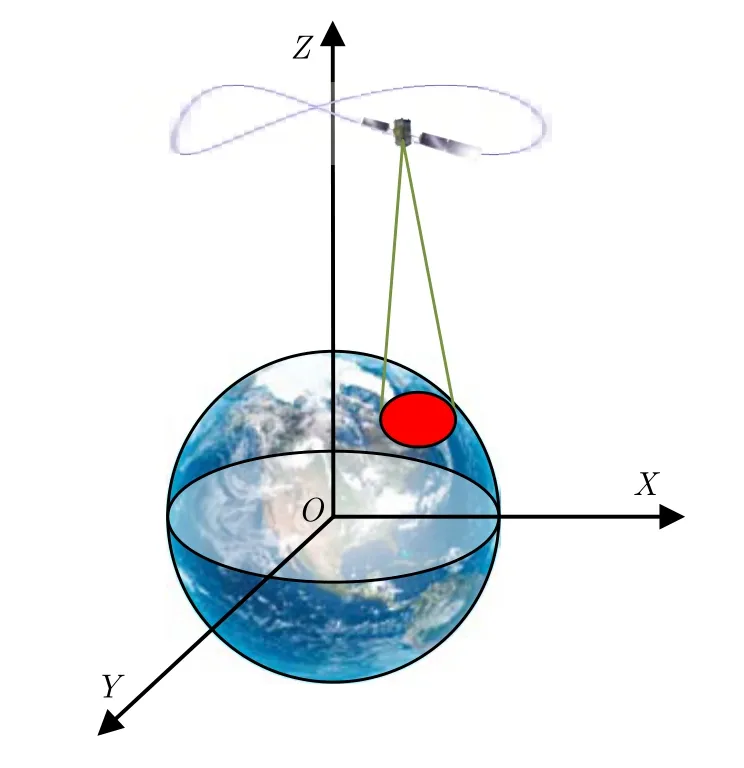
图24 非欧氏坐标系成像模型Fig.24 Imaging model in non-Euclidean coordinate system

CFBP算法对每个子孔径采用相同的直角坐标系成像网格，虽然避免了插值操作，但造成了子孔径图像的方位谱混叠，并且适用模式单一，仅适用于直线轨迹，对于曲线轨迹无法直接进行成像。而GCBP算法是一种改进的CFBP算法，其通过将成像网格布置在地面，避免了图像几何形变，并且改进频谱压缩函数，使其使用范围更加广阔。对于高轨SAR成像，由地表弯曲引入的二维相位误差会导致图像散焦，GCBP算法没有考虑地表弯曲所带来的方位相位误差，并且需要进行大倍数的上采样操作，计算效率较差。使用GCBP算法对曲面进行成像仿真，取场景左边缘点、中间点与右边缘点进行分析，其能量等高线图与剖面图如图25所示，可以发现使用地平面成像算法对曲面进行成像时，两侧点目标聚焦效果较差，成像精度较低。

图25 GCBP算法对地表曲面成像仿真结果Fig.25 Simulation results of GCBP algorithm for surface imaging

虽然对高轨SAR而言，此时成像地面不再是平面，但仍然符合直角坐标的定义，也就是罗氏空间的直角坐标，可以使用非欧氏几何学模型对三维场景中物体之间的相对位置与相互关系进行计算。因此，针对基于平面网格的快速BP算法均无法有效处理由于地表弯曲而引起的方位相位误差问题，文献[41]针对星载SAR成像提出了一种基于实际弯曲地表的快速BP成像方法，其主要流程如图26所示。首先，基于实际地表进行成像网格的布置。接着，针对子孔径图像的方位频谱混叠所带来的影响，建立二维子孔径图像与三维网格坐标之间的映射关系，采用一种改进的两步频谱压缩方法，第1步是将谱中心移动到网格中心处，第2步是方位频谱倾斜校正。其次，采用了多级图像合成方法来减少计算量，该方法能够避免大量的方位补零和图像域插值，在计算量和精确度方面均具有良好表现。最后将各个距离子场景的图像进行拼接，得到最终成像结果。目前，该技术已成功应用于世界首颗高轨合成孔径雷达卫星-陆地探测四号01星。

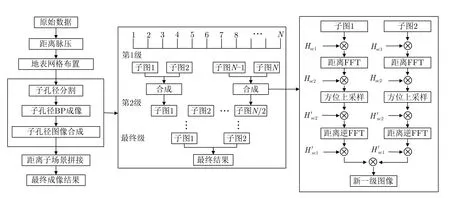
图26 文献[41]所提算法流程图Fig.26 Flow chart of algorithm proposed in Ref.[41]

为确保建立的成像网格能贴合地面，文献[41]将成像网格布置在经纬度坐标下，如图27所示。在建立经纬度坐标系下的成像网格后，若具备成像场景处的数字地形高程数据，可以通过插值获取每个网格点的海拔，在此基础上减去平均高程并进行补偿，以获得每个网格点的准确海拔。将成像网格点的坐标转换到地理坐标系下，并在距离向上对整个成像网格进行划分，此时整个场景的成像网格是基于场景中心点统一建立的，因此各个距离子场景图像在拼接时不用再进行几何校正处理。但是子孔径BP图像为二维图像，而曲面网格中的点目标为三维坐标，因此图像 (Ix,Iy)与成像网格方位向的中间行在场景坐标系下的坐标 (xc,yc,zc)的映射关系可近似为

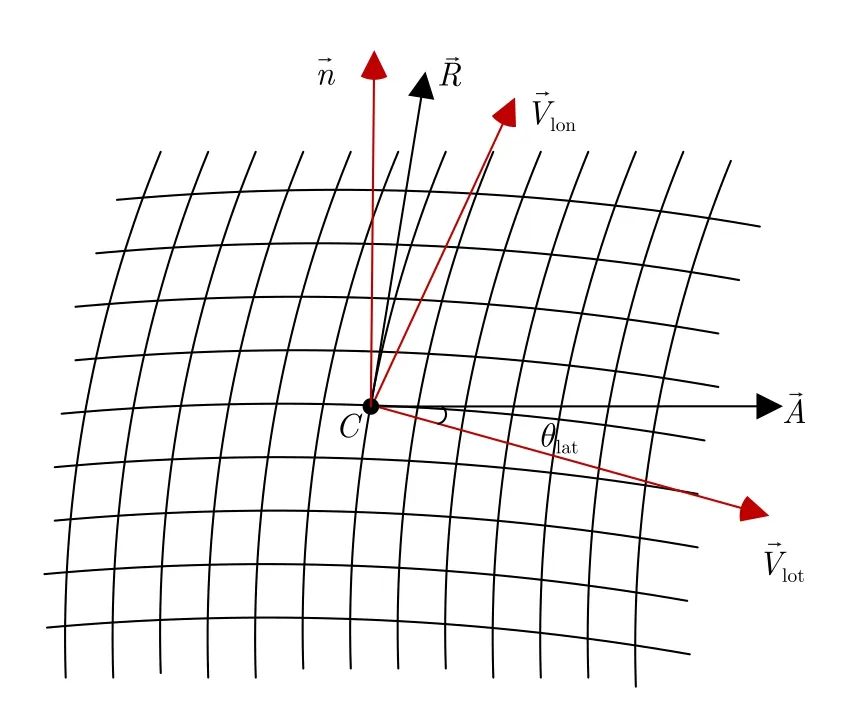
图27 文献[41]所提成像网格和方向向量示意图Fig.27 The schematic of imaging grid and direction vectors proposed in Ref.[41]

其中，k xn,n=1,2,3,4，kyi,i=1,2和kzj,j=1,2分别表示各个坐标的多项式系数。由于距离频域无法处理随距离空变的方位频谱展宽，因此Iy用其中心Iyc表示。基于两者的映射关系，可以得到两步谱压缩函数分别为式(14)与式(15)。其中K′为目标经过第一步谱压缩后的距离维波数支撑区范围，tc为当前子孔径的波束中心时刻。经过两步谱压缩后的方位波数谱宽度为

其中，θba表示方位波束宽度。

最后对两步谱压缩后的子孔径图像进行方位2倍上采样操作与逆两步频谱压缩处理，对子孔径图像进行相干融合即可得到最终成像结果。地理坐标系下快速BP算法实测结果如图28所示，可以发现其成像结果质量较好。

图28 文献[41]所提算法成像结果Fig.28 The imaging results of the proposed algorithm in Ref.[41]

假设原始数据的方位采样为La，成像网格方位向与距离向点数为N×N，包含n个子孔径与η个距离子场景。原始BP采用8倍插值处理。可以得到文献[41]所提算法计算量为

当N=16384,n=32时，文献[41]所提算法与原始BP算法计算量随方位采样数的变化如图29所示，其计算量明显小于原始BP算法。

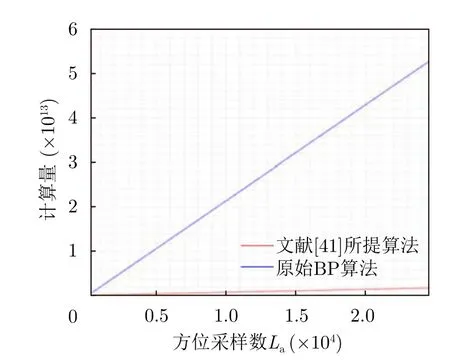
图29 文献[41]所提算法与原始BP算法的计算量对比Fig.29 Comparison of computational load between the proposed algorithm in Ref.[41] and original BP algorithm

6 结合运动补偿的快速BP成像

SAR平台飞行高度通常在百米至千米，位于大气对流层中，气流运动明显，气候复杂多变，容易受到气流等因素影响，造成飞行轨迹严重偏差，如图30所示，真实轨迹与理想轨迹间的误差难以忽视。相对于整个飞行轨迹而言，运动误差的量级较小，轨迹偏移并不大。在此情况下，快速BP算法并不会失效，但会使得成像结果存在散焦。一般情况下，使用惯性导航系统和全球定位系统进行运动误差轨迹。但由于现有的惯导技术无法达到聚焦成像所需的精度，仅依赖成像算法也难以满足实际的成像需求，会引起图像散焦与成像几何失真。因此，在SAR成像中，运动补偿技术的应用显得至关重要。

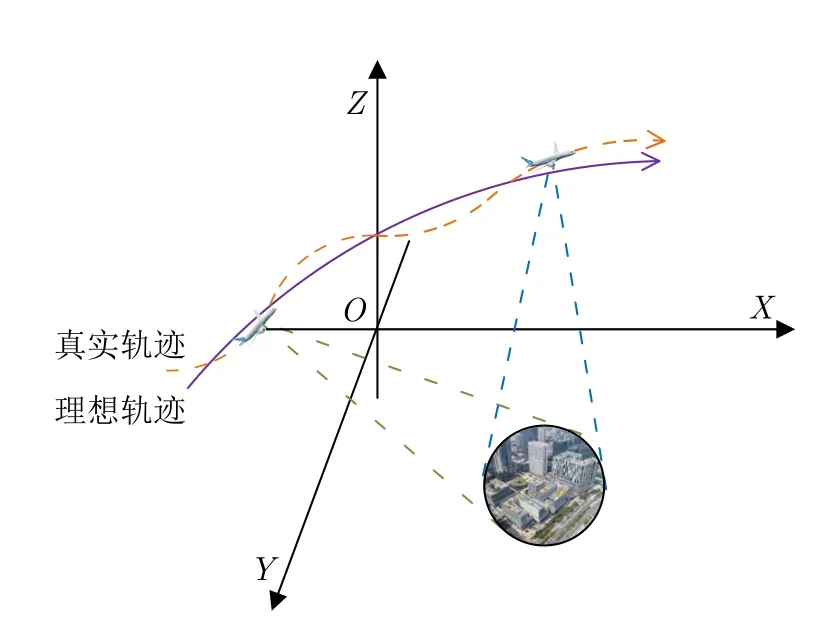
图30 实际成像轨迹模型Fig.30 Real imaging trajectory model

6.1 极坐标系下运动误差补偿技术

在极坐标系下进行快速BP成像时，可以使用适应度函数作为误差估计方法，例如采用图像锐化度等作为适应度函数进行相位误差估计。文献[42]使用BFGS优化算法进行误差估计，提出了基于离散余弦变换系数的最大图像锐化度相位校正方法来估计相位误差，虽然提高了计算效率，但使得估计准确度降低。文献[43]同样基于最大图像锐化度准则建立相位误差估计优化模型，并提出了一种针对FFBP算法的有效自动对焦方法，使用坐标下降法和割线法来获得闭合解，使得相位误差得到了很好的补偿。同理，该类方法也可适用于虚拟极坐标系下，文献[44]提出了一种结合广义锐化度指标与AFBP成像模型的两步时域自聚焦算法，分为子孔径自聚焦与子孔径图像相干积累两步骤，对子孔径使用遗传算法与最大化最大像素值方法来估计相位误差。但总的来说这类估计方法计算效率都不高，并且当局部BP图像存在非线性距离徙动时，难以正确估计相位误差。

不同于上述基于适应度函数的估计方法，快速BP算法还可以结合传统自聚焦算法进行运动误差补偿，例如相位梯度自聚焦(Phase Gradient Autofocus,PGA)[45,46]和图像偏移算法(Map Drift Autofocus,MDA)[47-49]。这类算法在2009年由Jakowatz和Wahl首先提出[50]，该种方法能够正确估计误差的一个必要条件是图像域和相应的距离压缩相位历程域信号之间存在近似的傅里叶变换关系。Zhang等人[25]以此提出了一种结合FFBP算法的多孔径图像偏移算法，在虚拟极坐标下成像得到子孔径图像，然后通过递归得到精确的相位误差函数，经过运动误差校正后得到聚焦良好的图像，使用该算法对实测数据进行成像，结果如图31所示，从数据处理结果看，图像得到了良好的聚焦。与传统的基于极坐标的FFBP算法相比，虚拟坐标系的相位误差可视为空间不变分量，便于估计和补偿，因此文献[51]同样在虚拟极坐标系下，结合FFBP算法和加权PGA来实现自聚焦，但对于超宽带条件下无法适用。而文献[52]提出在虚拟极坐标系下与FFBP算法相结合的多子带局部自聚焦算法，适用于超宽带条件下运动误差补偿，通过改进子孔径误差融合方法来适应孔径边缘的运动误差，并且使用改进的加权PGA方法得到运动误差的非线性映射关系。文献[53]提出了一种基于局部图像方位去斜和PGA的二维空变相位估计方法，可以结合极坐标系下的FFBP算法实现相位误差校正，但是方位去斜会导致剩余空变距离偏移和剩余空变方位相位，使得误差估计不准确。总的来说，这类算法的可行性基于近似的傅里叶变化关系，而机动平台SAR的机动性和超高分辨都会引起近似傅里叶变化关系的失效，其中轨迹的机动性造成的频谱形变与偏移，使得近似的傅里叶变化关系不存在，或者引入额外估计误差，这部分误差在长合成孔径的积累下将严重影响聚焦质量。

图31 文献[25]所提算法成像结果Fig.31 The imaging result of the proposed algorithm in Ref.[25]

6.2 直角坐标系下运动误差补偿技术

适用于直角坐标系BP成像的运动误差估计方法同极坐标系下相似，也可分为基于适应度函数的估计方法与结合自聚焦算法的运动补偿方法两类。Ash[54]基于最大化图像锐化度，提出了一种适用于聚束模式下BP成像的自聚焦方法(Autofocus Back Projection,ABP)，采用空间投影法进行相位误差估计，虽然获得高估计精度，但由于算法每次迭代都需对一个大型矩阵进行求逆运算，导致计算效率低下。文献[55]对文献[54]进行了改进，只选取少数像素点进行自动聚焦估计相位误差，减少了内存与计算时间的需求。但上述两种算法都没有意识到SAR图像的能量分布对ABP算法的性能有很大的影响，因此文献[56]提出了一种适用于低频SAR图像的自聚焦BP算法，通过选择区域和平衡数据的能量，有效地避免由于能量分布不平衡而引起的估计误差。文献[57]提出了一种与CFBP算法相结合的自聚焦算法，通过对CFBP算法中的谱压缩步骤进行修改，构造了补偿后的子孔径图像与直角坐标系下距离脉压后的相位历史数据之间的近似傅里叶变换关系，采用多孔径MD算法来获得相位误差信息，同时结合奇异值分解总体最小二乘法来提高估计的鲁棒性。该方法继承了CFBP算法的优点，能够校正残留的距离变化引起的相位误差。

但对于复杂轨迹SAR而言，其在距离-方位平面上成像时首先需要将复杂轨迹补偿为直线轨迹，这会引入新的误差，同时引入图像的几何形变[37]。此时，上述方法都将不再适用。并且雷达平台在实际飞行过程中存在三维方向误差，导致目标在直角坐标系下BP图像存在非线性距离徙动和方位相位误差，使得目标散焦。为此，文献[58]提出了一种基于反演数据域相位误差的运动误差补偿方法，适用于复杂轨迹聚束SAR的运动误差估计，其流程图如图32所示。

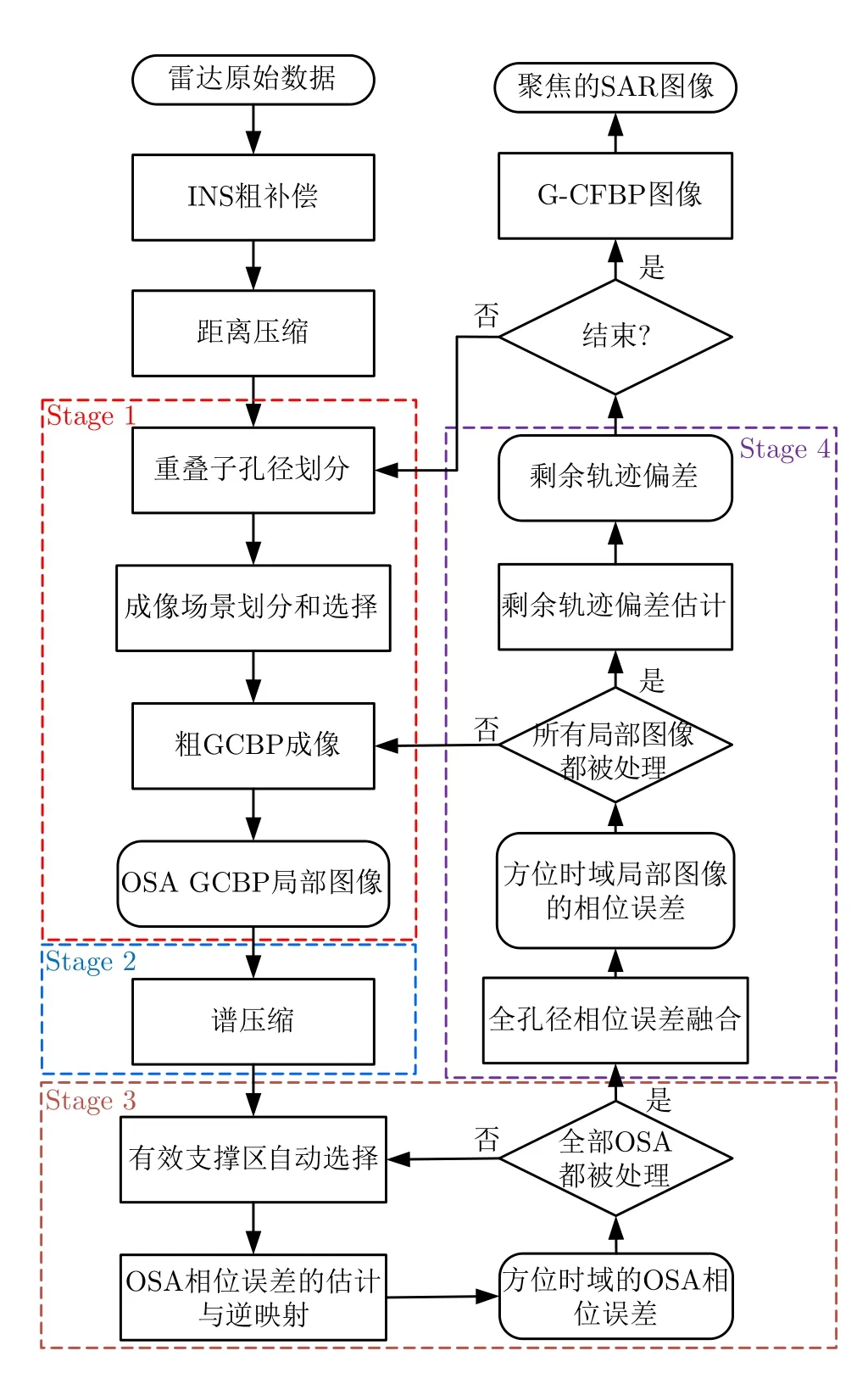
图32 文献[58]所提算法流程图Fig.32 Flow chart of algorithm proposed in Ref.[58]

通过求得BP图像频谱和系统发射频谱之间的关系，使用图像的距离谱范围求取有效的发射频率，构建相位误差映射网络。图33为映射关系示意图，其中黑色点为图像的频谱取值点，红色点为有效的距离向和方位向的发射频点，蓝色线框中黑色点处的误差为PGA估计的谱域相位误差。通过该解析的映射关系，可以从图像域的相位误差得到方位时域的相位误差。

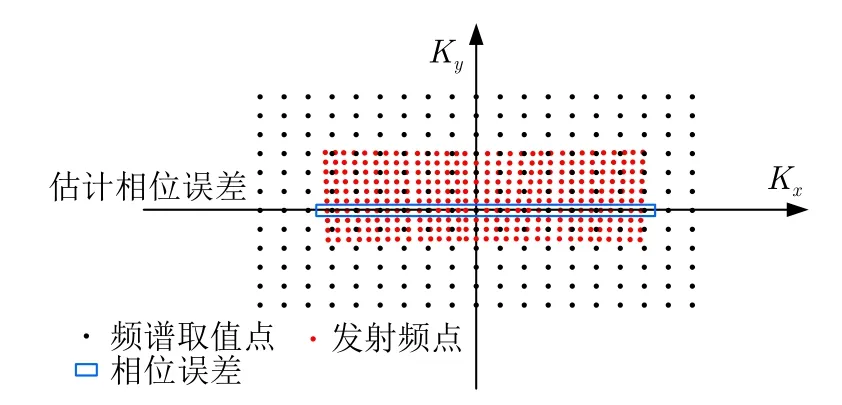
图33 文献[58]所提相位误差映射示意图Fig.33 Inverse mapping diagram of the phase error proposed in Ref.[58]

求得一系列子孔径相位误差后，需要将它们拼接成全孔径相位误差。然后对所有子孔径进行相干拼接得到全孔径相位误差。子孔径相位误差与拼接后的全孔径相位误差如图34与图35所示。对所有局部图像进行方位时域误差估计后，可以得到N个相位误差，用来估计剩余轨迹偏差，最后对理想轨迹中剩余轨迹偏差进行补偿，利用GCBP算法得到良好聚焦图像。

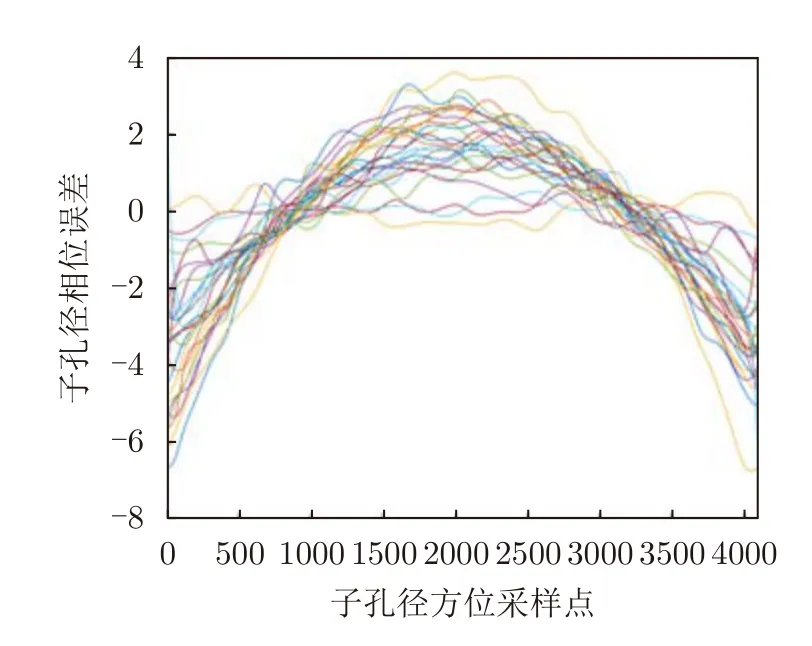
图34 子孔径相位误差Fig.34 Sub-aperture phase error

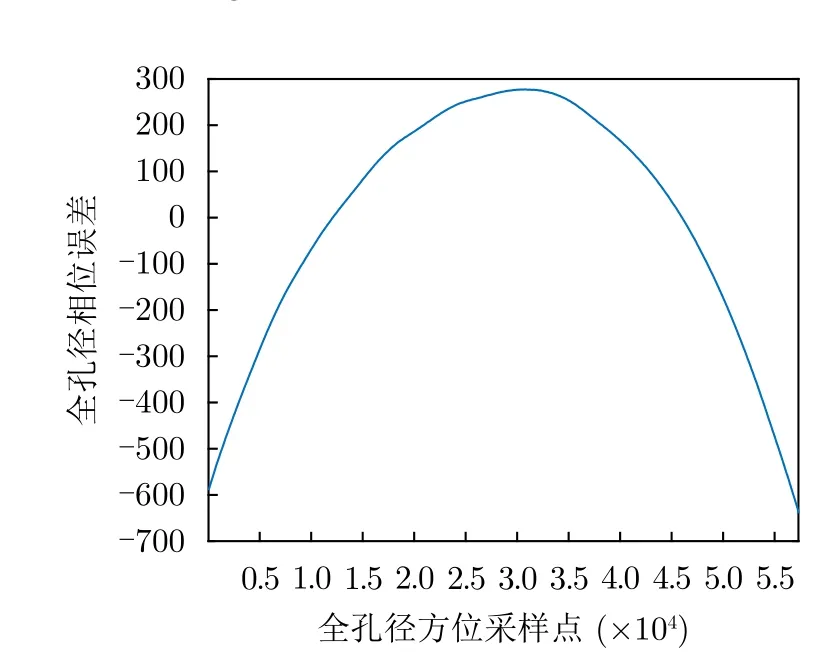
图35 全孔径相位误差Fig.35 Full aperture phase error

使用实测数据对文献[58]所提运动误差补偿方法进行验证，运动补偿前后结果如图36所示。可以发现运动误差补偿后的成像结果，得到了良好的聚焦。

图36 文献[58]所提运动误差补偿算法成像结果Fig.36 The imaging results of the proposed MoCo method in Ref.[58]

假设方位向采样点数为La，重叠子孔径数为m，子孔径图像数量为D，大小为N×N，在使用GCBP算法进行成像时，划分子孔径数为n，文献[42]、文献[52]与文献[58]的计算量分别如表4所示。为方便比较，假设m为63时，三者计算量如图37所示，可以发现文献[58]所提算法计算量最少。

表4 文献[42]、文献[52]与文献[58]所提算法计算量对比Tab.4 Comparison of computational burden between algorithm proposed in Ref.[42],Ref.[52] and Ref.[58]

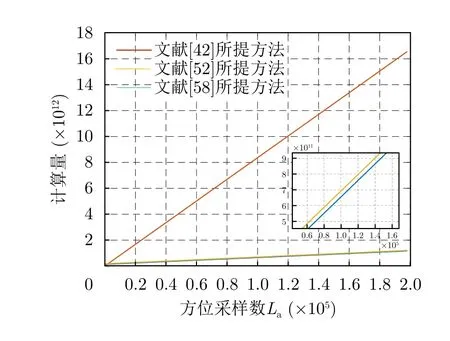
图37 文献[42]、文献[52]与文献[58]的计算量对比Fig.37 Comparison of computational load between Ref.[42],Ref.[52] and Ref.[58]

7 总结展望

各类成像面坐标系下的快速BP算法的研究与应用，使得SAR成像应用场景越来越广泛。相较于传统BP算法，其能在保证成像质量的同时，使得计算效率更快，满足实时成像需求。同时，直角坐标系下快速BP算法的发展为快速BP算法的发展注入了新的生命，成像效率与成像质量得到提升的同时，适用场景也越来越广泛。

直角坐标系下快速BP算法与极坐标系下快速BP算法，除了计算量上的差异外，两者所使用的插值方式也不同。这是影响它们在实际应用中执行效率的一个重要因素。与直角坐标系下的快速BP算法采用FFT插值实现方位上采样操作不同，极坐标系下快速BP算法在各级图像融合时一般采用sinc插值实现。而FFT插值通常比sinc插值执行速度更快，特别是在处理大量数据时。在工程应用中，快速BP算法的实现往往会结合图形处理器(Graphics Processing Unit,GPU)、数字信号处理器(Digital Signal Processor,DSP)和现场可编程门阵列(Field Programmable Gate Array,FPGA)等硬件设备。其中，GPU的管理能力(处理器对任务调度和资源管理的能力)较弱，但具有强大的浮点计算能力及高度并行的架构，使其在处理可并行任务时具有显著优势。快速BP算法中的分级迭代过程，下一级子孔径图像生成依赖于若干上一级子孔径图像数据，每一级的处理过程可以通过调用GPU中的核函数实现。同时，GPU适合进行整块数据的流处理算法，适用于回波数据全部录取完后的成像处理过程，充分利用其多进程并发的特性。对于需要实时成像的场景，DSP与FPGA更加适合。DSP的管理能力较弱，但其运算能力较强，在实时信号处理任务中表现出色。而FPGA既能管理也能运算，提供了较高的灵活性和潜在的效率，但其开发难度相较于前两者更复杂。在实时成像过程中，极坐标系下快速BP算法，例如FFBP算法，需要录取两个或以上的子孔径回波数据并成像后，才能进行下一步图像融合处理。并且生成的每一级子孔径图像数量都需大于等于2，才可以进行下一步处理，直至得到最终成像结果。而直角坐标系下快速BP算法，录取完一个子孔径大小的回波数据并成像处理后，便可与之前的结果进行相干索引叠加，不需要等待下一个子孔径回波数据，更适用于实时成像处理。综上所述，实际选择哪种硬件平台取决于具体应用场景、性能需求、开发资源以及功耗等多方面因素。

近年来，随着各类快速BP算法在SAR成像领域使用率的增加，以及雷达观测平台模式变得多样化，轨迹变得复杂化，快速BP算法存在着较大的发展空间，从现有的研究状况分析，对未来的发展趋势进行预测：

(1) 多种模式统一的快速BP算法。目前的各类快速BP算法需要针对不同的成像场景选择相应的成像面坐标系布置成像网格，因此，在未来对快速BP算法的研究中，如何设置一种通用的坐标系来布置统一的成像网格，适用于不同成像场景，对快速BP算法的广泛使用具有重要作用。

(2) 沿着灵活波束进行成像的快速BP算法。在面向对象的灵活观测模式中，使用快速BP算法沿波束扫描轨迹布置成像网格，能以更少的重访次数实现对场景的扫描，并且能适应任意场景与轨迹，灵活度与回波利用率更高，将成为之后SAR成像模式研究的主要方向之一。

(3) 与各类高性能运算平台结合的快速BP算法。目前各类快速BP算法在工程应用领域较少，尤其是直角坐标系下快速BP算法。与GPU等各类高性能运算平台结合可以大幅提升快速BP算法的计算速度，使其能够应用于更广泛的实际场景。因此，与各类高性能运算平台相结合的快速BP算法将会进一步推动快速BP算法在工程应用领域的发展。

(4) 适用于三维成像的快速BP算法。目前的快速BP算法成像大都应用于二维成像，布置二维成像网格。若将成像网格设置成三维，使其适用于三维成像将进一步提高快速BP成像算法的发展空间。但如何提高三维成像时的计算效率与精度依旧是快速BP算法发展的重要挑战。

利益冲突所有作者均声明不存在利益冲突

Conflict of InterestsThe authors declare that there is no conflict of interests