深埋隧道支护结构内力计算方法研究

赵何霖, 邱居涛, 申玉生,2*, 朱鹏霖, 苟安迪, 董俊

(1.西南交通大学交通隧道工程教育部重点实验室, 成都 61003; 2.西南交通大学陆地交通地质灾害防治技术国家工程研究中心, 成都 610031; 3.中铁第四勘察设计院集团有限公司, 武汉 430063)

随着中国城市化建设进程的加快,以地铁为主导的地下轨道交通快速发展,地面及浅部城市地下空间资源已不能满足城市发展的需求[1],深部地下空间的开发利用正当其时。目前,中国大部分城市地下空间开发深度主要集中在50 m以浅[2],现有的浅部地层荷载计算理论难以支撑深部地下空间设计与施工,而深部地下空间开发所处的地质条件千差万别,地下空间结构设计、施工面临一系列新的挑战。

迄今为止,众多学者针对深埋隧道结构理论解析进行了大量研究分析,取得了一些研究成果。在无支护作用下隧道围岩应力位移解析法方面,Zhao等[3]基于复变函数理论,研究了不同侧压力系数条件下深埋矩形隧道的应力解。张道兵等[4]基于非线性Hock-Brown破坏准则,采用极限分析上限定理得到了深埋硐室围岩压力的最优上限解。王文州等[5]基于非线性Hoek-Brown强度准则,研究了深埋隧道开挖导致的围岩应力和位移解析解。刘淑红等[6]基于复变函数方法,得到了开挖引起的深埋非圆形隧道围岩弹性和黏弹性变形解析解。吴利华等[7]结合平面应变解析解和V-D(09)位移释放率方程,得到了三维圆形隧道弹塑性解析解。对于考虑支护结构作用隧道开挖与支护应力解析方面,Lu等[8]基于柯西解法,引入应力释放系数,得到考虑衬砌、围岩相互作用的深埋隧道应力解析解。徐强等[9]基于深埋隧道开挖后衬砌支护与围岩相互作用分析,提出了基于松动圈理论的围岩压力计算方法。杜小洲等[10]基于收敛约束法,结合非圆形隧洞围岩解析与可视化软件,提出了一种隧洞解析应力空间分布呈现方法。陈登国等[11]基于Drucker-Prager准则与理想弹塑性本构关系,得到了非均匀应力场下圆形隧洞弹性区应力场解析表达式。张治国等[12]基于Mohr-Coulomb准则,得到了深埋隧道在渗流力作用下围岩和衬砌结构相互作用的弹塑性解析解。Qiu等[13]考虑了隧道开挖速度和岩体应力释放的影响,基于黏弹性理论推导得到了深埋隧道径向位移和支护反力解析解。综上所述,目前对于深埋隧道力学响应的研究成果多集中在隧道围岩应力和位移上,对于支护结构考虑较少,而判断隧道衬砌截面最不利位置往往需要综合考虑结构轴力、弯矩和剪力等因素。因此,有必要对深埋隧道支护结构力学响应进行深入研究。

鉴于此,在考虑到支护结构力学响应的空间差异性及施工过程围岩-支护结构的动态作用关系情况下,推导了围岩压力作用下初支与围岩、初支与二衬间协同作用的解析解,与数值分析算例和现场实测结果进行了对比验证,最后探讨了隧道支护参数对该解析方法的影响,以期为支护结构的施工设计提供理论基础。

1 深埋隧道支护结构内力计算方法

1.1 隧道结构分析模型与解析式

研究表明,对于高为h,宽为b的马蹄形断面隧道可将其等效为半径为R的圆形隧道[14-16],如图1所示,等效公式如式(1)所示。

(1)

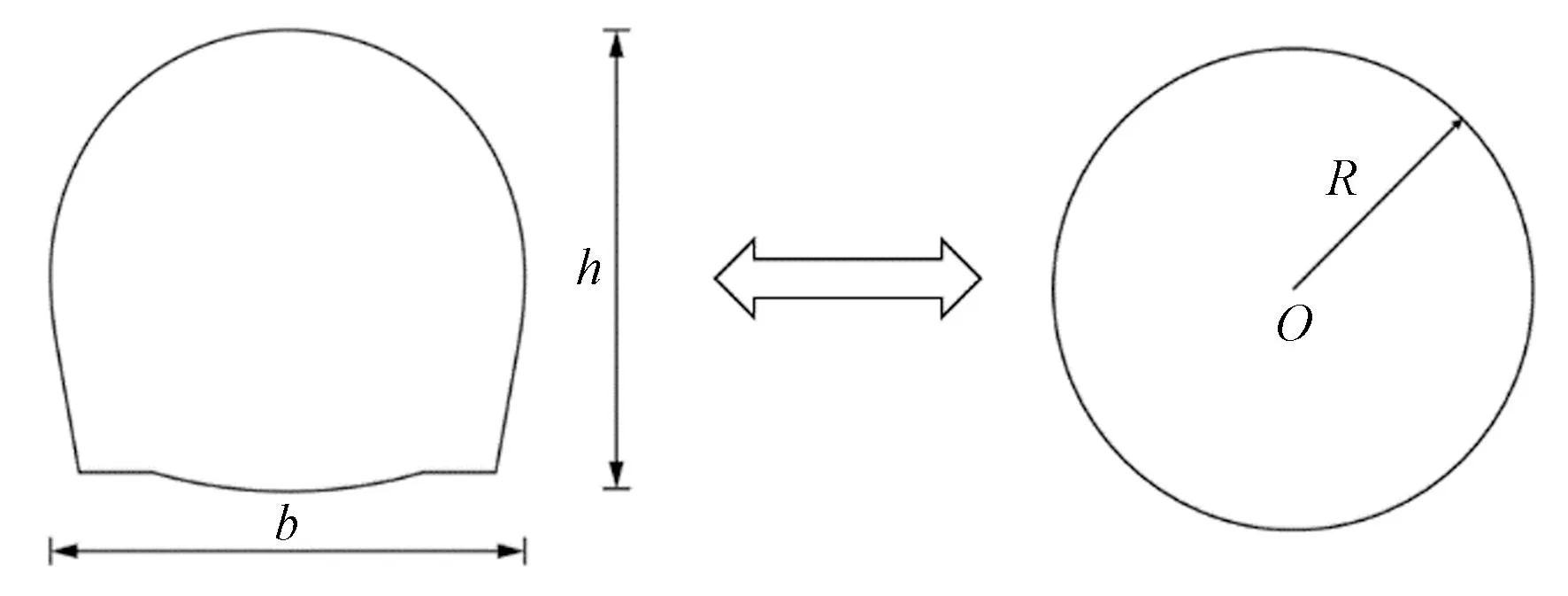
图1 等效圆转化示意图Fig.1 Schematic diagram of equivalent circle transformation

对于深埋隧道,可将其视为无限大平面内的孔洞问题。模型中假定围岩和衬砌都为弹性体,且围岩与衬砌完全接触,不考虑地下水影响。取衬砌圆环的部分作为微元体进行受力分析,为便于计算,需要将衬砌在直角坐标系下的受力转换为极坐标系进行分析,如图2所示,环向角度φ以逆时针为正,衬砌在竖直围压q和水平围压λq的作用下受到轴力N、弯矩M和剪力Fs的共同作用,σρ、τρφ分别为极坐标系下圆环径向正应力和切应力。

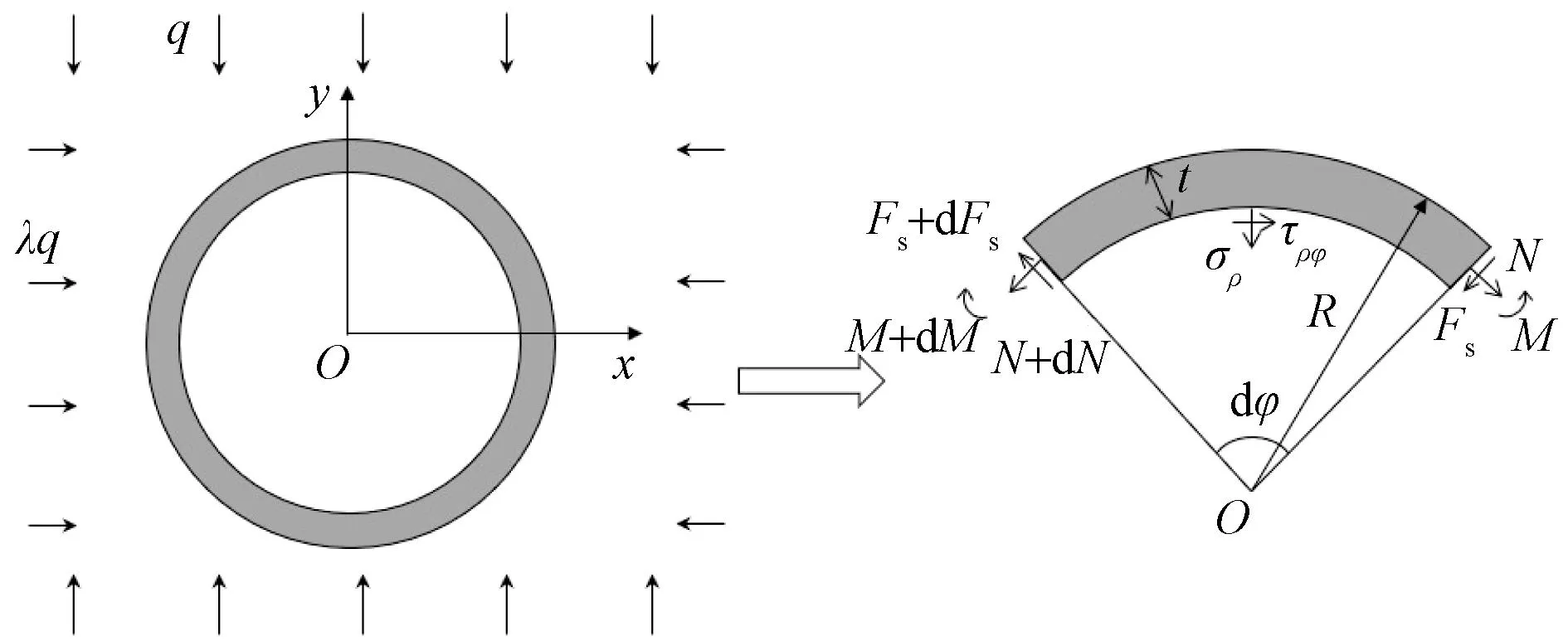
图2 衬砌圆环受力分析示意图Fig.2 Schematic diagram of the mechanical analysis of the lining element

根据直角坐标到极坐标的坐标转换公式为

(2)

式(2)中:σx为直角坐标系下x轴方向正应力;σy为y轴方向正应力;τxy为xy平面上剪切应力;σφ为极坐标系下圆环环向正应力。

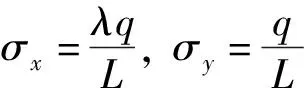
(3)

式(3)中:λ为侧压力系数;L为结构纵向单位长度;q为作用于围岩的竖向荷载。

根据孙振宇等[16]的研究,其平衡控制方程可表示为

(4)

式(4)中:K为支护结构的抗弯刚度,可表示为

(5)

式(5)中:E为衬砌弹性模量;v为泊松比;t为支护结构厚度。

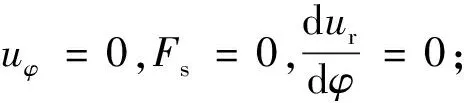
(6)

假设隧道以恒定速率掘进,在距掌子面x1的位置开始设置初期支护,距掌子面x2的位置开始设置二次衬砌,如图3所示。

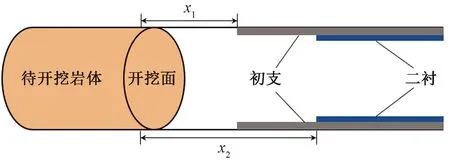
图3 隧道开挖与支护的纵向施工顺序Fig.3 Longitudinal construction sequence of tunnel excavation and support

根据张平等[17]的研究,掌子面后方任意处的围岩径向位移表达式为

(7)

式(7)中:β为位移释放系数;p0为上覆岩土体自重应力;x为分析断面距掌子面的距离;m(φ)为环向角度φ的函数。

p0=γh

(8)

式(8)中:γ为岩土体容重;h为隧道埋深。

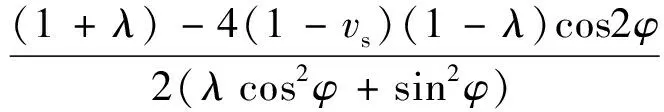
(9)

式(9)中:vs为围岩的泊松比。

隧道径向位移的表达式为

(10)

式(10)中:p1为隧道开挖面空间效应产生的虚拟支护力;p2为支护反力,p1和p2共同承担围岩荷载;Es为围岩的弹性模量。

1.2 隧道初支施加后围岩压力与位移解析解

隧道开挖后由于围岩自身的约束作用承担了一部分荷载,在支护施作前,假设存在沿隧道径向的虚拟支护反力p1,由其承担围岩压力,如图4(a)所示。厚度为t1的初支施作后,总的支护反力为p′2,p′2由虚拟支护反力p1和初支提供的支护反力p2构成。

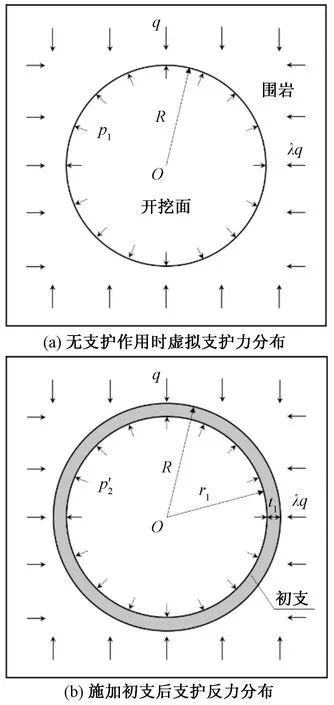
图4 围岩-初支相互作用分析示意图Fig.4 Schematic diagram of the interaction between the surrounding rock and the primary lining

当p2=0时,可得无支护作用时沿隧道纵向的围岩径向位移为

(11)

从而可以推出p1的表达式为

p1=(1-β)p0

(12)

根据关宝树[18]的研究,可得沿隧道纵向初支的支护反力的表达式为

(13)

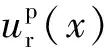
初期支护的结构刚度的表达式为

(14)

式(14)中:r1=R-t1,其中t1为初期支护厚度;E1和v1分别为初期支护的弹性模量和泊松比。

将式(12)、式(13)和式(11)代入式(10),即可得到初期支护施作后隧道纵向的径向位移为

(15)

将式(15)代入式(13)得初期支护沿隧道纵向的支护反力为

(16)

将式(16)代入式(3)可得初支与围岩相互作用力q为

(17)

1.3 隧道二衬施加后围岩压力和位移解析解

如图5所示,假定初期支护(厚度为t1)与二次衬砌(厚度为t2)变形协调且初支处于弹性状态,初支与围岩完全接触且等效为一个整体。

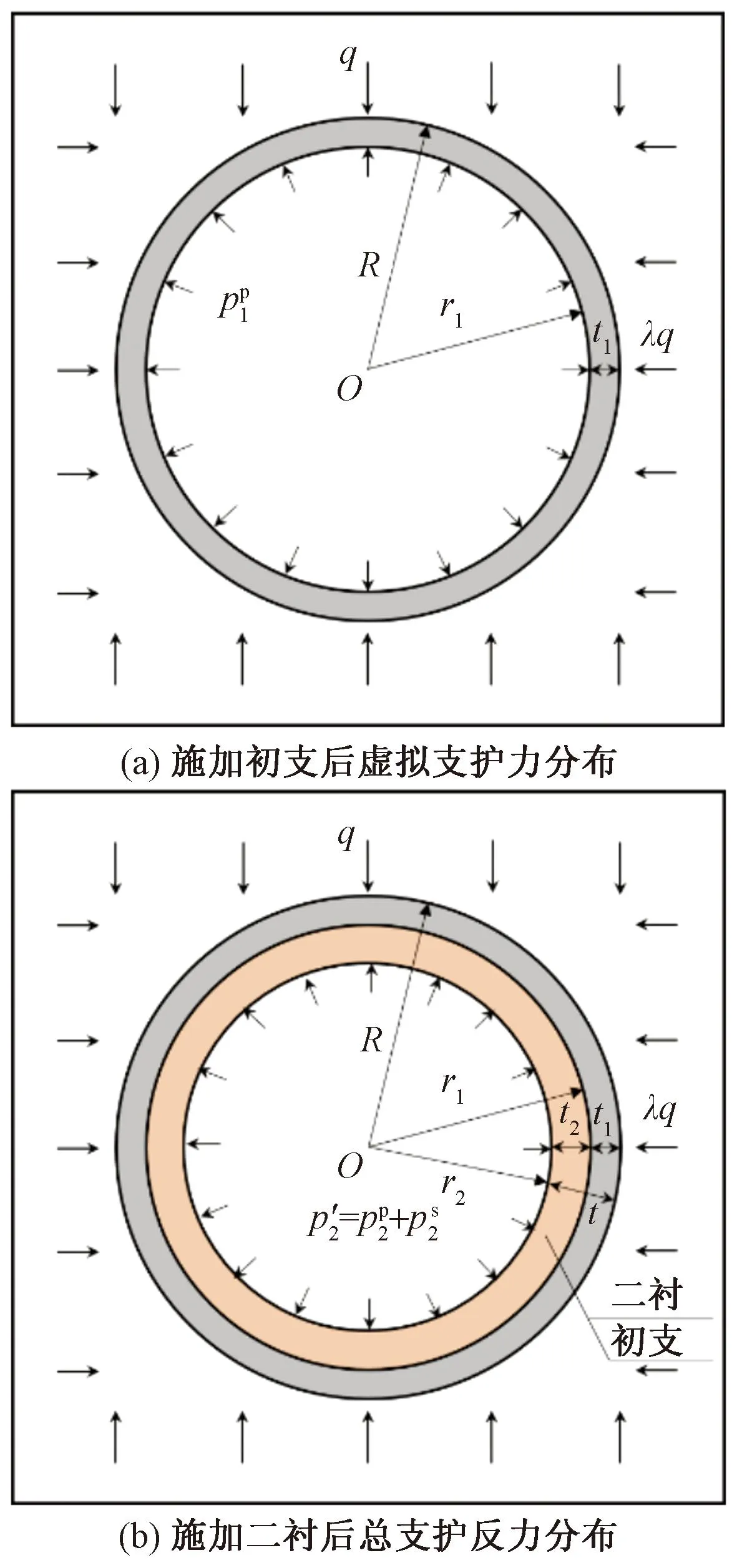
图5 初支-二衬相互作用分析示意图Fig.5 Schematic diagram of the interaction between the primary lining and the secondary lining

(18)

同理可得沿隧道纵向总支护反力的表达式为

(19)

隧道衬砌结构刚度表达式为

(20)

式(20)中:E2和v2分别为二次衬砌的弹性模量和泊松比。

将式(18)和式(19)代入式(10)可得

(21)

从而可得二次衬砌支护后初支、二衬的支护反力为

(22)

将式(22)代入式(3)即可得到初期支护、二次衬砌协同作用解析式q1和q2,分别表示为

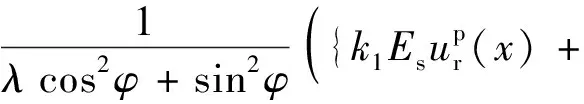
(23)

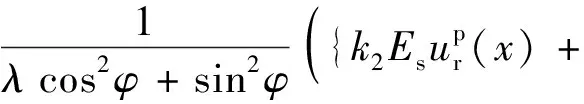
(24)

将式(23)、式(24)分别代入式(6)即可得到深埋隧道初支和二衬的内力解析式。

2 解析解的验证

2.1 理论计算与数值模拟对比

为验证隧道衬砌内力解析式的理论可靠性,采用三维有限差分软件FLAC3D进行数值分析对比,考虑到边界效应影响,模型大小取100 m(长)×80 m(宽)×153 m(高),计算模型如图6所示,模型均采取8节点的6面体实体单元,模型共计包含324 000个单元和335 478个节点。模型的前后左右及底面均施加位移约束条件,地表为自由面。隧道围岩、初期支护和二次衬砌均采用线弹性本构模型,围岩和衬砌材料的物理力学参数如表1所示。隧道采用全断面开挖法模拟,开挖循环进尺为2 m,选取模型中间断面进行研究。

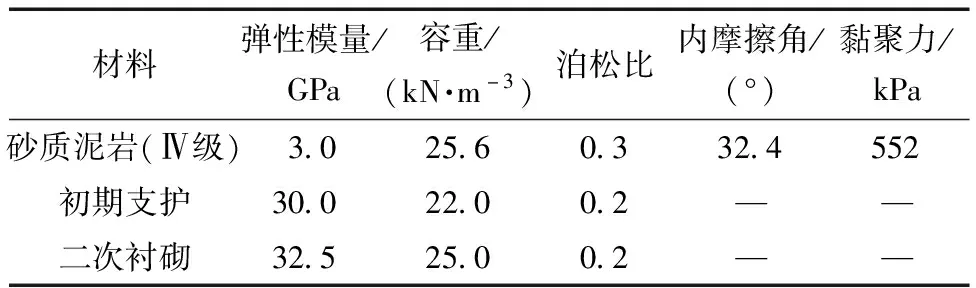
表1 围岩和支护结构物理力学参数Table 1 Physical and mechanical parameters of the surrounding rock and support structure

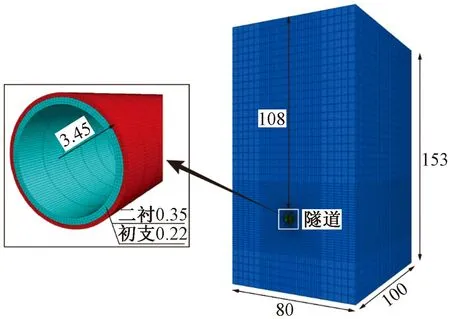
图6 隧道数值模拟计算模型Fig.6 Numerical simulation model of tunnel

理论计算与数值模拟得到的围岩压力和围岩径向位移对比如图7、图8所示。可以看出,采用理论计算与数值模拟得到的隧道围岩压力和径向位移的变化规律基本一致,且数值模拟值略大于理论值,可能是由于数值模拟中监测断面在掌子面未到达之前受到应力扰动,然而在理论计算方法中并没有考虑到这一点。理论计算与数值模拟得到的围岩压力均在开挖10 d趋于稳定,其峰值分别为264.2、290.3 kPa。此外,两者得到的隧道径向位移最小值位于拱顶和拱底,分别为1.1、1 mm,从拱顶(0°)到左拱腰(90°)随着角度的增大,变形也随之增大,拱腰处变形最大,分别为5.6、4.9 mm。

图7 拱顶围岩压力时程曲线对比Fig.7 Comparison of the surrounding rock pressure on tunnel crown

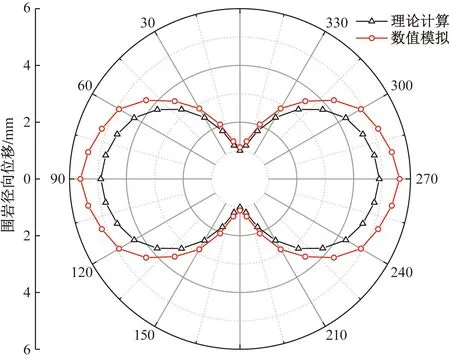
图8 围岩径向位移对比Fig.8 Comparison of the surrounding rock radial displacement

解析方法得到的围岩径向位移值与数值模拟结果的对比如表2所示,可以看出,两者围岩径向位移的偏差在11%～14.4%,说明理论计算值与数值模拟值吻合较好,从而验证了理论计算方法的可靠性。

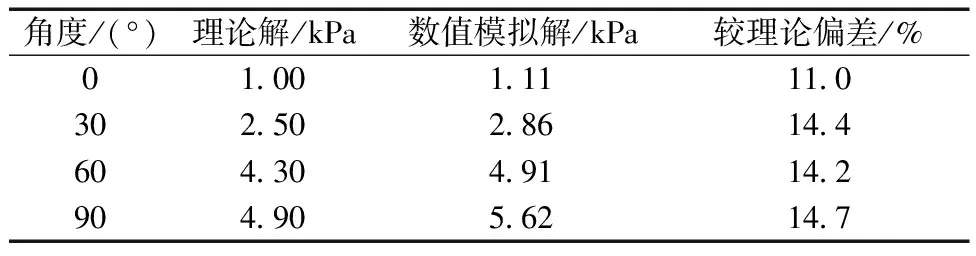
表2 理论计算与数值模拟结果比较(围岩径向位移)Table 2 Comparison of theoretical calculating results and numerical simulation results (the surrounding rock radial displacement)

2.2 理论计算与现场监测对比

依托重庆地铁18号线富华路-歇台子站区间隧道工程,隧道采用全断面法施工,围岩为中风化砂质泥岩,Ⅳ级。区间隧道标准断面为马蹄形断面,断面尺寸宽7.02 m,高6.78 m,隧道埋深在28～108 m之间。在区间隧道开挖过程中,选取了典型试验断面,对隧道围岩压力、钢拱架内力等进行监测。断面的详细测点布置如图9所示,图10为现场部分仪器安装过程。为了进一步验证所提出的计算方法有效性,将理论计算结果与现场监测结果进行对比分析。在理论计算中,基于等效公式将现场区间隧道马蹄形断面等效为直径6.9 m的圆形断面隧道,其他参数取值如表1所示。

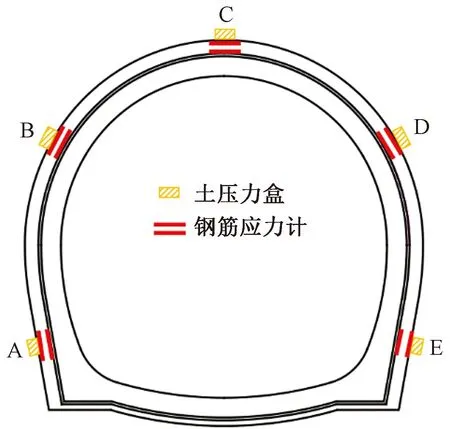
A～E点分别代表左拱脚、左拱腰、拱顶、右拱腰及右拱脚图9 隧道断面测点布置图Fig.9 Layout of the measured points of tunnel cross section

图10 现场监测仪器的布置Fig.10 Arrangement of in-situ monitoring instruments

以现场108 m埋深的施工监测断面为分析对象,得到的隧道围岩压力和初期支护轴力对比分别如图11、图12所示。可以看出,根据理论计算得到的结果与现场监测数据变化规律基本一致,两者的围岩压力在前期均急剧增大,随后增速减缓,直至收敛稳定,两者围岩压力最大值分别为264.2、220.1 kPa。理论计算中的围岩压力在开挖10 d稳定,而现场在开挖14 d后趋于稳定,原因为现场全断面开挖时,围岩受爆破影响较大,前期数据大幅波动。对于初期支护轴力,理论计算和现场监测的轴力均为正值,说明初期支护整体受压力作用,两者的轴力均呈近似对称分布,最大值皆位于拱脚,分别为49.7、43.2 kN,最小值均位于拱腰,30.6、27.0 kN。对于初期支护结构,其受力具有明显的空间差异性,在施工中可根据需求对不同部位补强。

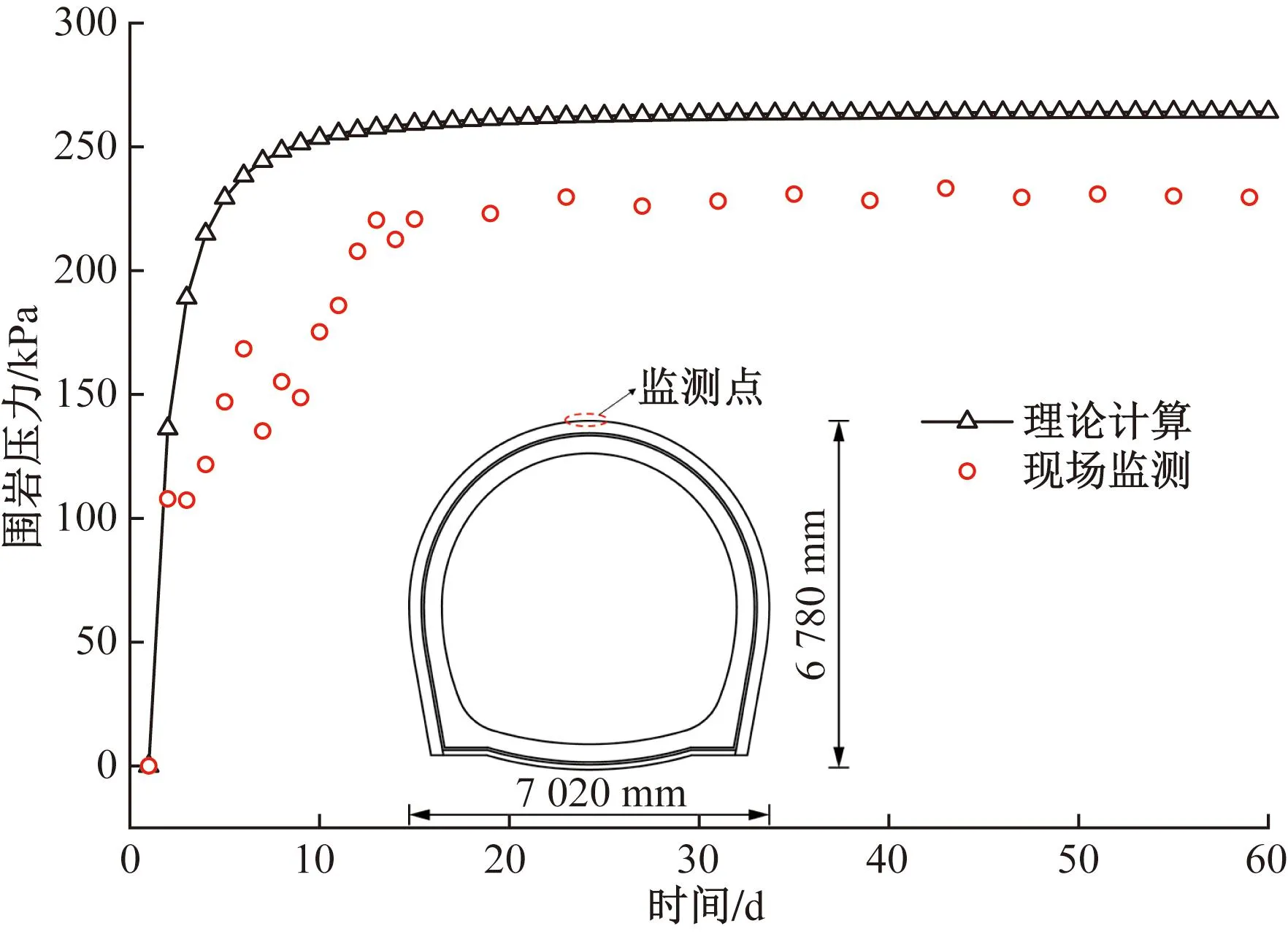
图11 拱顶围岩压力时程曲线对比Fig.11 Comparison of the surrounding rock pressure on tunnel crown

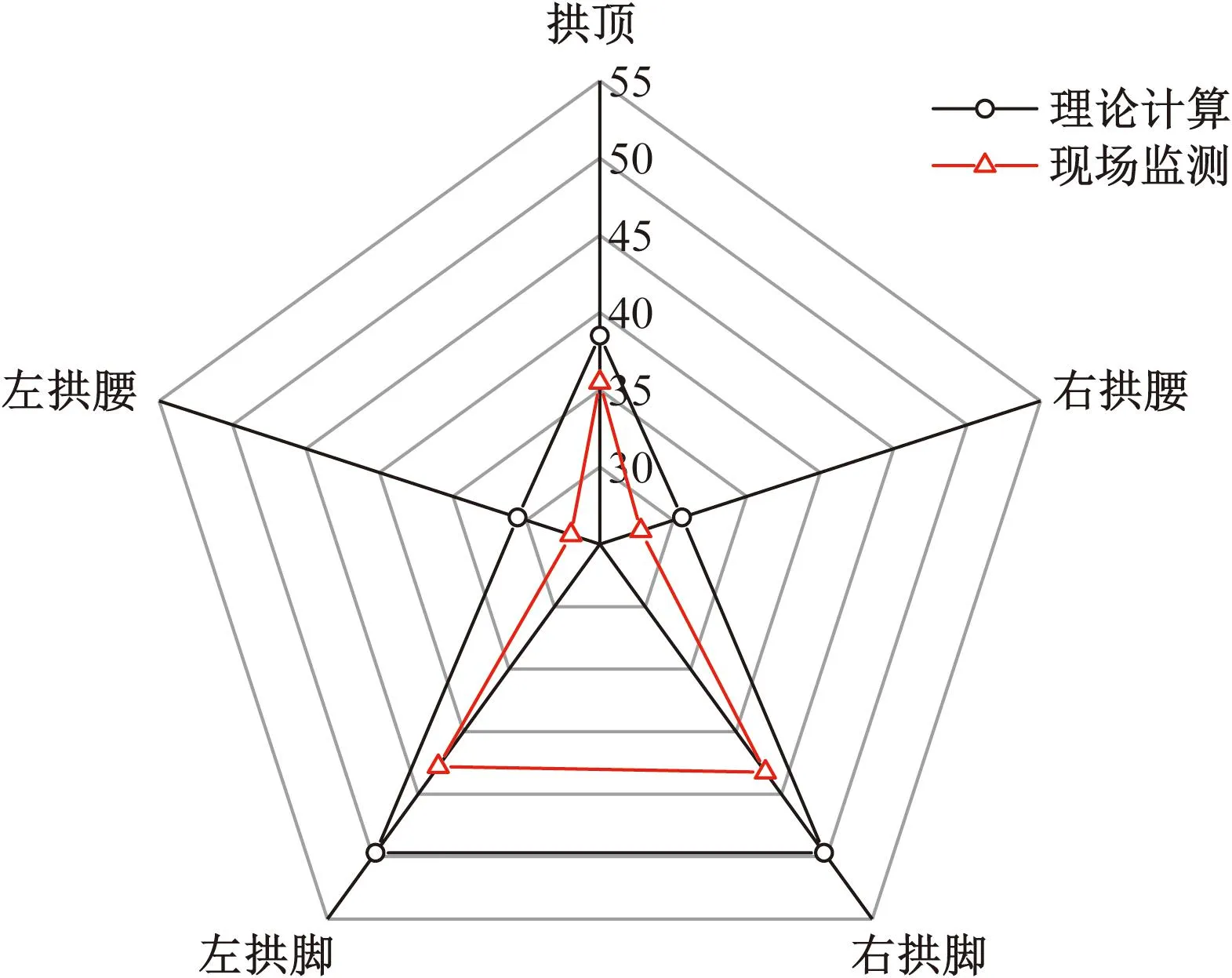
图12 初期支护轴力对比Fig.12 Comparison of the primary lining axial force

表3为解析方法得到的初支轴力值与现场监测值的对比,可以看出,理论计算结果均大于现场实测值,两者初期支护的轴力偏差最小为7.8%,最大可达13.9%,原因在于理论计算结果是基于弹性理论得出的,这与现场围岩的实际情况有所不同,且现场施工中会采取如注浆加固、锚杆设置等加固措施,然而本文计算方法没有考虑这些因素。总的来说,所提理论计算方法能有效预测深埋隧道围岩压力和支护结构轴力,为指导现场的施工组织设计提供理论支撑。

表3 理论计算与现场监测结果比较(初支轴力)Table 3 Comparison of theoretical calculating results and field monitoring results (the primary lining axial force)

3 隧道支护结构参数分析

为明确隧道支护结构设计参数对理论计算结果的影响,采用控制变量法探讨初支厚度及其弹性模量、二衬厚度及其弹性模量等参数对支护结构内力、围岩压力和围岩变形的影响规律,详细参数取值如表4所示。

表4 支护结构参数取值Table 4 The values of the parameters of the support structure

图13分别给出了隧道初支(二衬)厚度及其弹模与拱顶处初支(二衬)弯矩、位移和拱顶围岩压力的关系曲面图,其中弯矩受拉为正,受压为负。可以看出,拱顶处的初支(二衬)弯矩与初支(二衬)厚度和弹模正相关,且弹模的变化对弯矩的影响更显著。例如,当弹模为32 MPa时,初支厚度从0.2 m增长到0.35 m其弯矩增加了3.7%。当初支厚度为0.2 m时,弹性模量从0.5 MPa增加到32 MPa其弯矩增加了1901.7%;初支厚度和弹模越大,隧道拱顶处围岩压力越大,沉降越小,而随着二衬厚度和弹模的增加,隧道拱顶处围岩压力和沉降都随之增加;初支、二衬厚度及弹模的变化对拱顶沉降影响都较小,但初支厚度和弹模的变化对其影响比二衬更大。例如,当支护结构厚度一定时,初支和二衬的弹模从1 MPa增大到32 MPa,拱顶沉降分别减小了17.1%和增加了3.6%;初支、二衬参数对围岩压力影响较大,且初支厚度和弹模对其影响明显大于二衬,当支护结构厚度一定时,初支和二衬的弹模从1 MPa增大到32 MPa,拱顶围岩压力分别增加了616.0%和58.4%,说明初期支护协助围岩承载作用比二次衬砌显著。

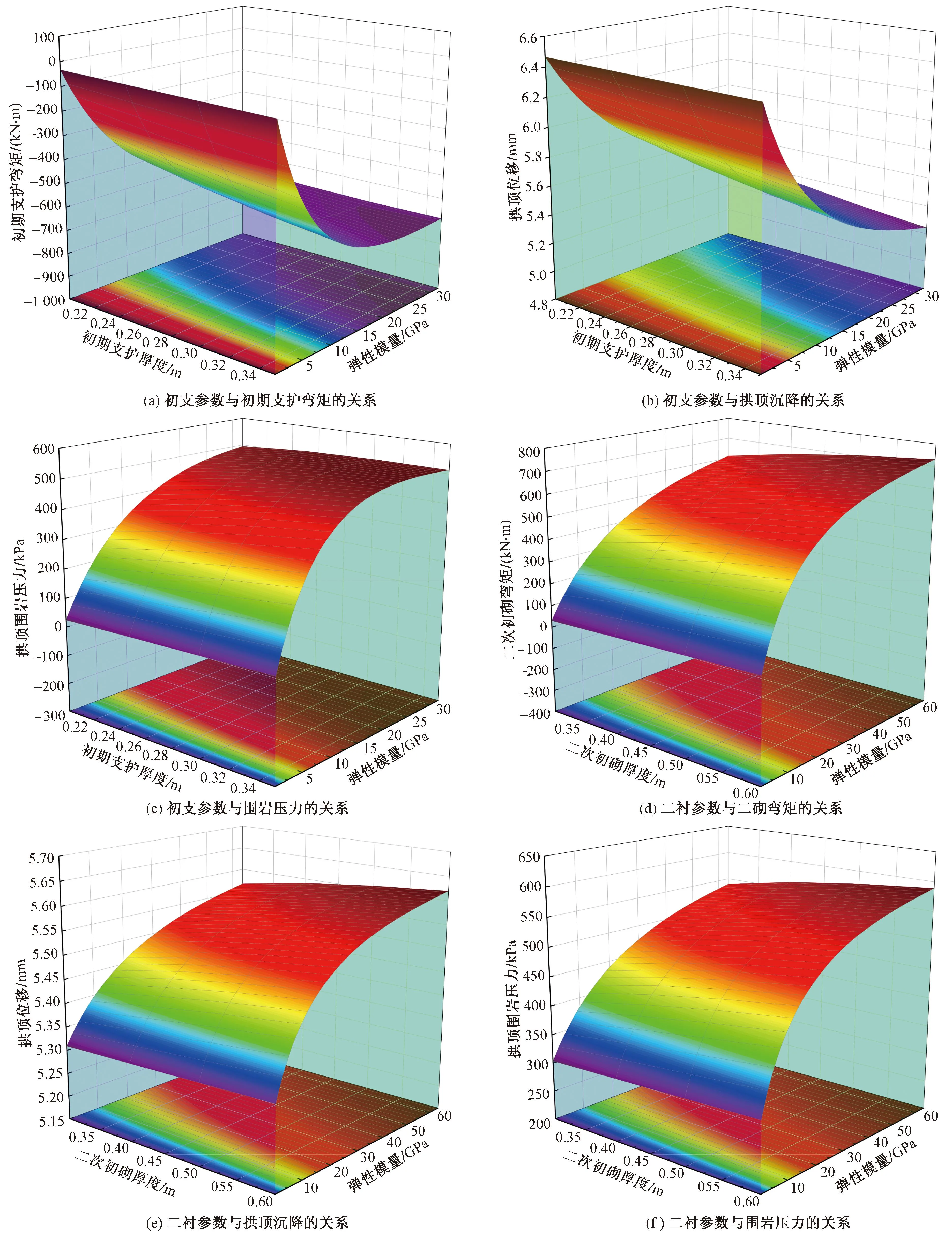
图13 支护厚度及其弹模与计算结果的关系Fig.13 Relationship between thethickness of the support structure and its elastic modulus and the calculation results

4 结论

采用理论分析、数值模拟与现场测试相结合的方法,对深埋隧道复合衬砌内力计算方法开展研究,得出如下主要结论。

(1)建立支护结构力学分析模型,获得支护结构内力计算公式,基于支护反力与围岩径向位移的关系,推导围岩压力作用下初支与围岩、初支与二衬的协同作用解析解。该方法考虑了支护结构力学响应的空间差异性和隧道施工过程围岩-支护结构的动态作用关系,能准确判断施工过程中支护结构的薄弱位置。

(2)采用数值模拟对解析解进行验证,稳定后数值解的围岩压力要超出解析解的9.9%,两者径向位移间的偏差在11%～14.4%,吻合较好。此外,将该方法成功应用于重庆轨道交通18号线区间隧道施工中,验证了该方法的可靠性和有效性。

(3)隧道支护结构的厚度和弹性模量与其弯矩正相关,且弹性模量对其弯矩影响更大。与二衬相比,初支厚度和弹模的变化对围岩压力和径向位移的影响更显著,表明支护过程中初支协助围岩承载的作用大于二衬。