基于向量角度差和拟合曲线融合的建筑物点云提取方法

刘茂华, 陈杰, 陈晗琳

(沈阳建筑大学交通与测绘工程学院, 沈阳 110168)

建筑物的提取在城市规划、数字制图以及更新地理信息系统数据库等众多领域中具有重要意义。近年来,航空激光雷达(light detection and ranging,LiDAR)技术因其具有高密度和高精度的点云数据而迅速发展,并成为提取建筑物的一种替代方法[1]。

目前,已经有大量的研究致力于建筑物提取。一些方法采用了将LiDAR数据与图像数据结合的策略[2-4]。邓飞等[5]利用方向和梯度等信息以及基于活动轮廓的图割算法,成功提取了建筑物的轮廓信息。王春林等[6]综合利用LiDAR数据和影像特征,在复杂场景中实现了建筑物轮廓的提取。尽管LiDAR和图像结合的方法可以提高准确性,但也存在一些问题,如在数据融合过程中需要设置合适的阈值,以及融合后可能导致精度降低等挑战。因此,为了克服上述困难,研究人员开始关注从单独的LiDAR数据中提取建筑物信息。

点云领域中的建筑物提取方法通常分为有监督方法[7-8]和无监督方法[9-10]。有监督方法利用算法如支持向量机[11]、随机森林[12]和深度学习[13-15]等。这些方法在点云分类方面具有一定的优势,但也存在一些限制,如参数调整和重复计算特征会降低准确性和计算效率。无监督方法包括形态学、区域生长、拟合方法和扫描线等技术。李昂等[16]结合梯度约束滤波、标记分水岭变换和最大似然分类等方法提取建筑物。赵传等[17]通过提取初始建筑物轮廓点、计算点云分布特征、聚类和区域增长等步骤实现建筑物提取。李强等[18]通过地面LiDAR点云数据的特征分析和构建规则集提取建筑物。朱军桃等[19]通过点云投影、边缘点提取、角点提取和边界线还原等步骤提取建筑物轮廓。吕富强等[20]通过去噪、聚类和点云分割提取建筑物,实现了自动化的建筑物点云提取。

处理大规模高密度LiDAR数据的主要挑战之一是计算负担。航空LiDAR系统中的扫描线提供了适合使用(graphics processing unit,GPU)进行并行计算的一维数据结构,使得处理高密度区域的LiDAR数据更加高效。一些研究已经在其方法中利用了扫描线。如在点云滤波[21-22],道路标线提取等[23]。Han等[24]和Hu等[25]基于扫描线成功的提取了建筑物,然而,在这种方法中,当植被具有非常平坦的冠层或建筑物具有粗糙和不规则的屋顶表面时,可能会产生错误的结果。这是因为该方法对建筑物屋顶表面的粗糙度和多样性作了不适当的假设。

综上所述,尽管以前的工作在某些方面取得了进展,但在功能和性能方面仍存在重要的限制。为了解决这些限制,提出一种基于向量角度差的屋顶提取算法。该算法利用航空LiDAR获取数据时的扫描线与x-o-y平面垂直,并且扫描线上相邻点具有相同维度的空间向量的特点,将三维空间向量简化为二维方向向量,然后计算方向向量与z轴之间的角度,并设置阈值角度来提取建筑物的屋顶平面。该方法能够在有效提取建筑物平面屋顶的同时,降低计算复杂度。提出一种基于欧氏距离和多项式曲线拟合的特征提取方法,用于提取曲线建筑物屋顶。首先,计算扫描线上相邻点之间的欧氏距离。然后,执行基于最小二乘法的曲线拟合。由于植被点分布是无序的,而建筑物屋顶表面是有序的,拟合曲线的平均残差值可以有效地提取建筑物曲面屋顶。

1 方法提出

通过LiDAR扫描线数据建立索引,采用k-维树(k-dimension tree,KD-tree)搜寻算法对点云数据进行去噪,同时依靠布料模拟算法(cloth simulation filter, CSF)对点云数据进行滤波处理,达到提取非地面点云的目的。首先,分别以每一条扫描线为研究对象计算非地面点的相邻方向向量并求差,利用样本确定差值阈值并提取出平面建筑物屋顶点云;其次,利用剩余点云的相邻点欧氏距离进行曲线拟合,得到曲面建筑物屋顶点云;最后,经过细化后处理,对提取后数据中的植物点进行剔除,得到完整建筑物点云数据的结果。算法流程如图1所示。

图1 本文算法流程图Fig.1 The proposed algorithm flowchart

1.1 扫描线模型

目前,机载LiDAR点云数据的获取扫描方式分为:有线扫描、圆锥扫描以及显微光学扫描。本文算法针对的数据模型是应用最为广泛的有线扫描式,这种扫描方式的激光脚点投影在地面上形成“Z”形。图2展示有效扫描的数据形式。图3展示了一条扫描线的剖面图。

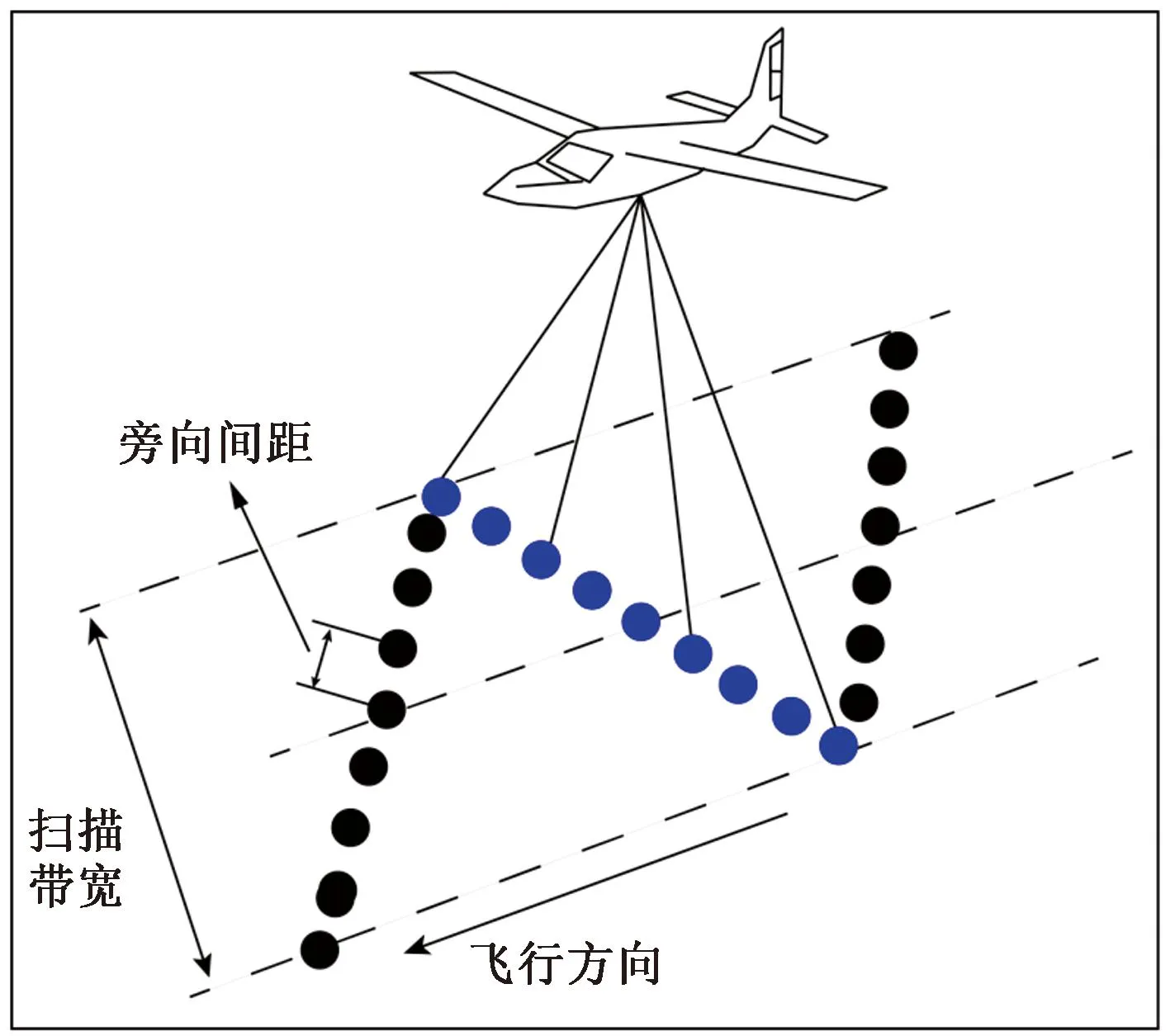
蓝色为一条扫描线图2 扫描线模型Fig.2 Scan line model

1.2 基于方向向量的平面屋顶点云提取

1.2.1 向量角度差

机载LiDAR获取点云数据时,运动方向平行于x-o-y平面,因此每条扫描线所在的平面与x-o-y平面垂直,可以使用该平面上所有方向向量与z轴之间的角度来区分平面和非平面。如图4所示,x-o-y平面即三维点云沿着z轴后的投影平面,则投影面法向量nm为(0,0,1),θi为相邻点的方向向量ni与nm的夹角。

红色点为建筑物屋顶点;黄色点为建筑物立面点;蓝色点为地面点;绿色点为高大植被点;棕色点为低矮植被点图3 扫描线剖面图Fig.3 Scan line profile

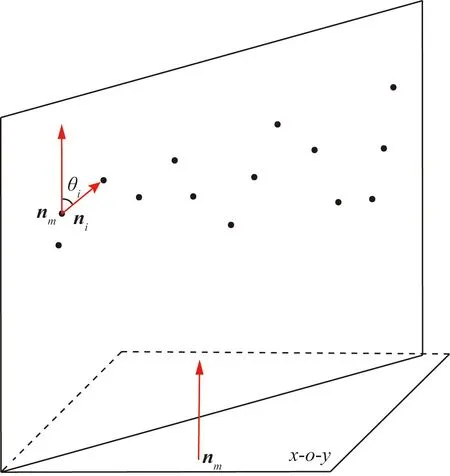
图4 向量角模型Fig.4 Vector angle model

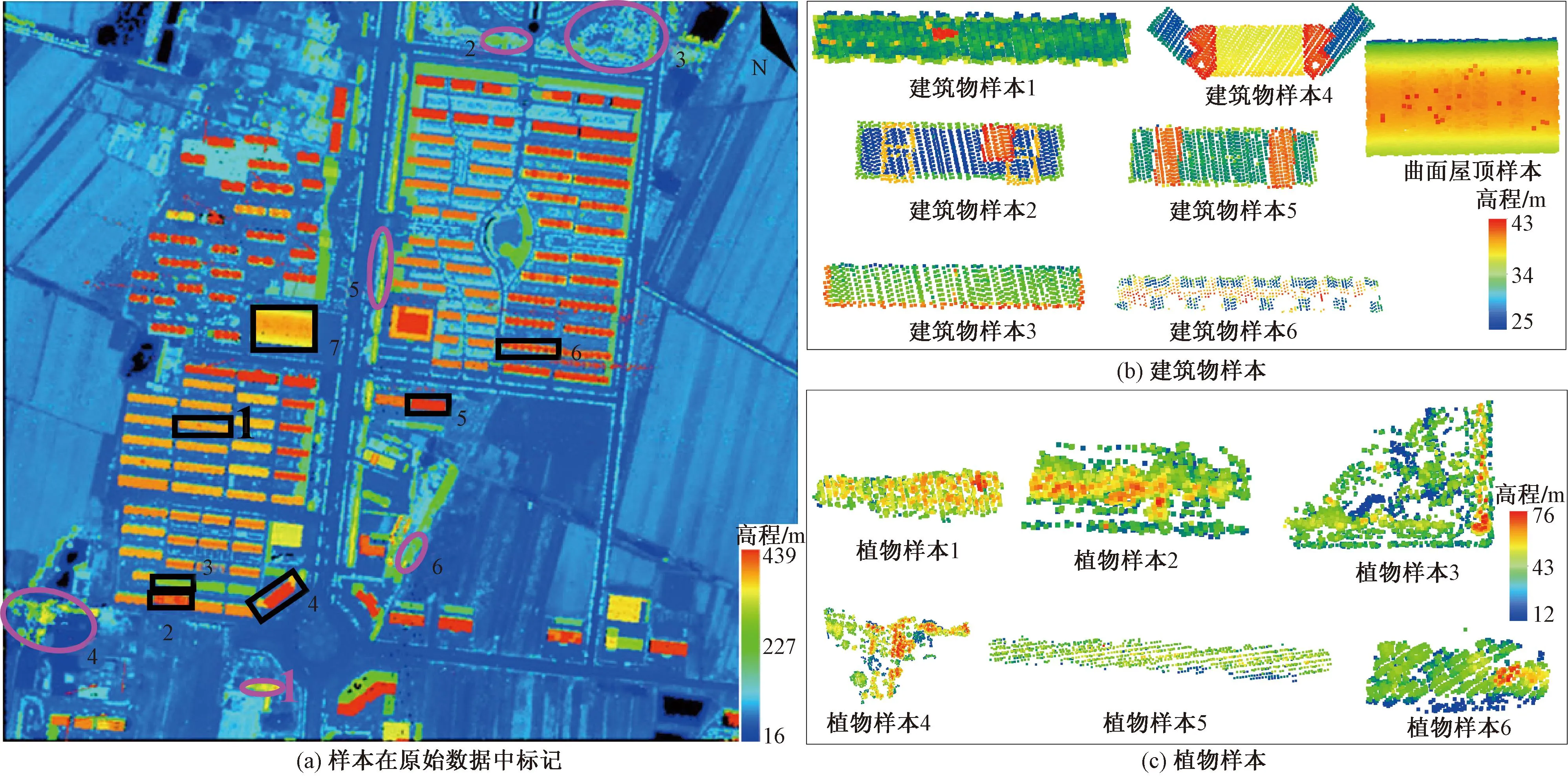
黑色框1～6为建筑物样本;黑色框7为曲面屋顶样本;红色圈1～6为植物样本图5 样本数据来源Fig.5 Source of sample data

得到非地面点后依次计算相邻点之间的方向向量夹角θi可表示为

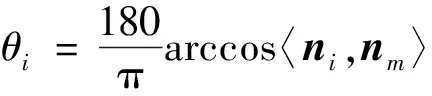
(1)

则相邻夹角的差值为

Δθi=θi+1-θi

(2)

1.2.2 角度差阈值确定

选取7个建筑物和6个植物样本进行实验计算,样本来源如图5所示。通过统计相邻夹角差值来确定区分平面与非平面的角度差阈值。建筑物样本中包含平顶,斜顶,高程变化复杂以及四周突起等建筑物,能充分表达城区内平顶建筑物的种类。

如图6所示,建筑物样本的相邻向量角度差高度集中在0°～15°,差值波动的主要原因在于:一是建筑物屋顶表面不是完全平滑的;二是扫描仪本身存在高程值与真实值存在误差。大于30°以上的差值是因为建筑物屋顶由多个平面构成而存在高度差。分别以10°、15°和20°作为阈值统计角度差的概率。

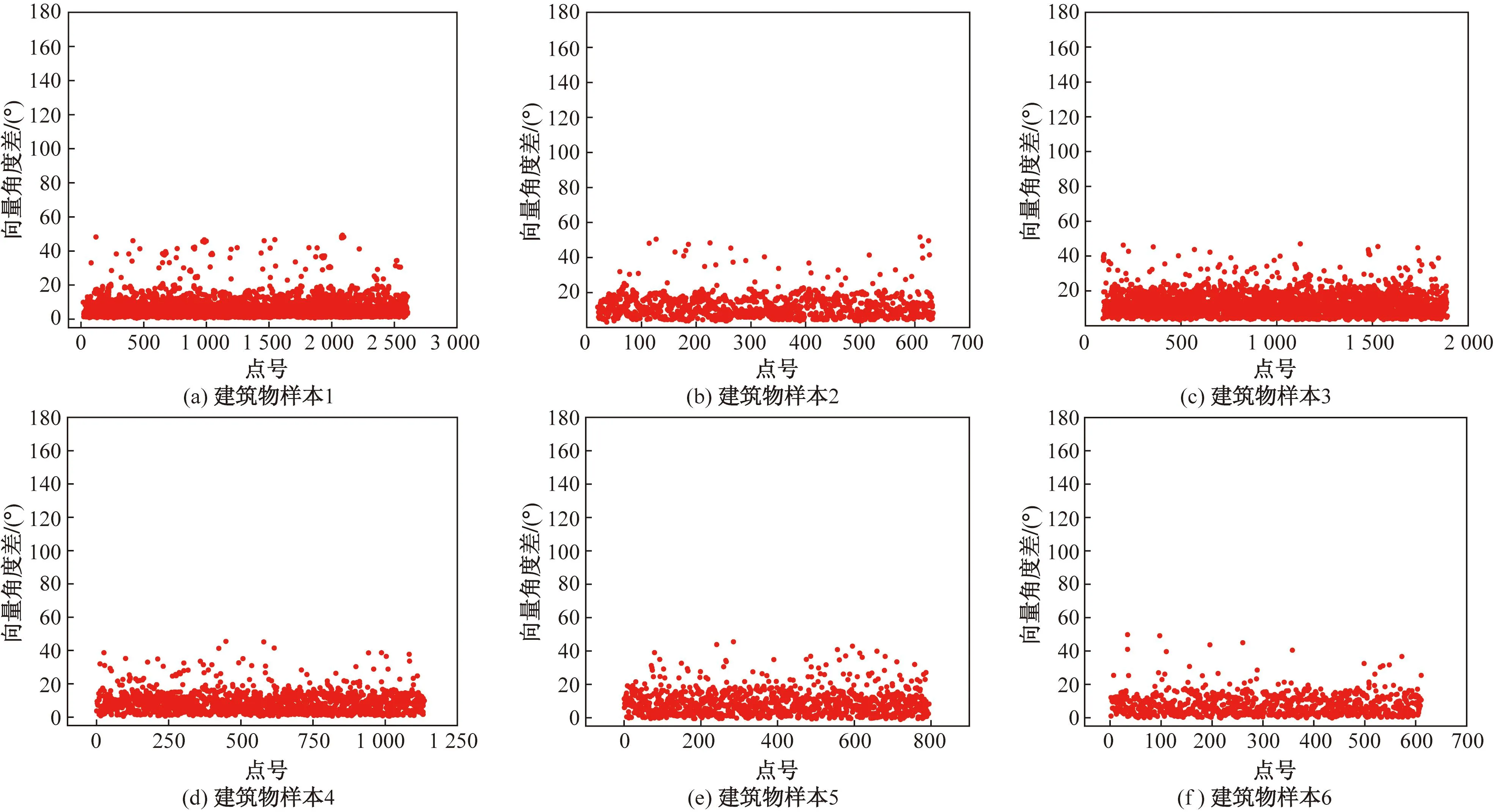
图6 6个建筑物样本直方图Fig.6 Histogram of 6 building samples

各样本数据如表1所示,平顶建筑物的相邻向量角度差高度集中在20°以内,而阈值分别设置为10°、15°以及20°时,平均概率分别为83.91%、95.96%和97.69%。以10°为基准,阈值设置为15°时,概率增长率(增加的概率与原本概率比值)为14.4%;阈值为20°时概率增长率为16.4%。说明当阈值设定为15°时的有效性提升远高于阈值设定为20°,这意味着提取建筑物时的准确率提升明显。

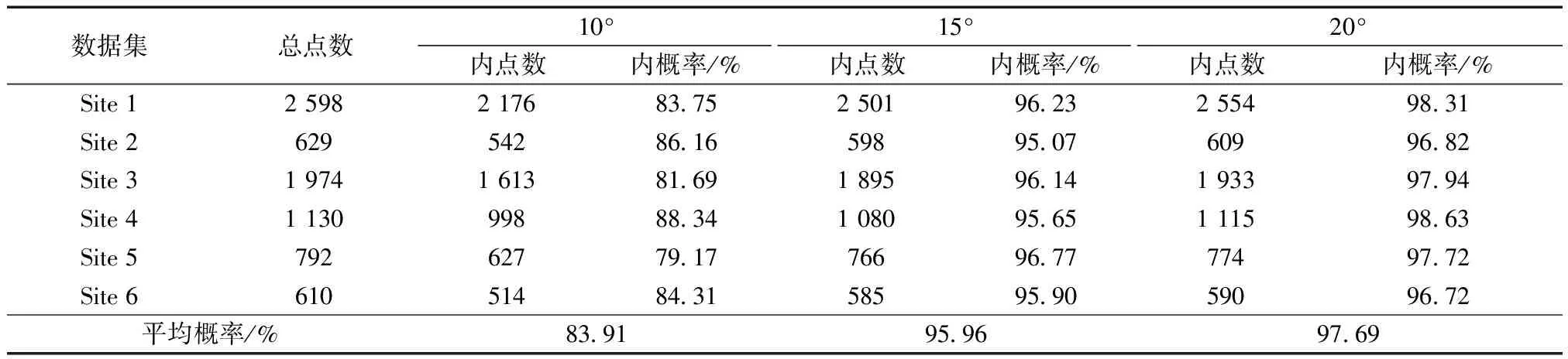
表1 建筑物样本数据

此外,为验证阈值普适性,选取6簇植物群样本进行相同计算。图7为6簇植物样本的相邻向量角度差,与平面建筑物不同的是,植物群向量夹角的分布是比较分散的,样本中角度差不均匀分布在角度的各个分段,其中更多的是集中在角度中段且跨度较大。

与建筑物样本取相同阈值进行比较,详细样本数据如表2所示。3个阈值下植物点分布概率分别为2.96%、4.69%以及8.47%,以10°为基准,15°的增长率为58.5%、20°的增长率为186.1%。这意味着,随着角度差的增大,提取建筑物时植物引起的误差逐渐增大。综合建筑物样本与植物样本的阈值结果,阈值从10°增大到15°,提取建筑物的准确率增加明显,且植物引起的误差较低;阈值从15°增加到20°时,建筑物的提取准确率增长变缓且植物引起的误差增加明显,故将提取平面屋顶的向量角度差阈值设置为15°。对于分类为非平面点的建筑物点和分类为平面点的植物点可以利用后续的细化后处理进行修正。

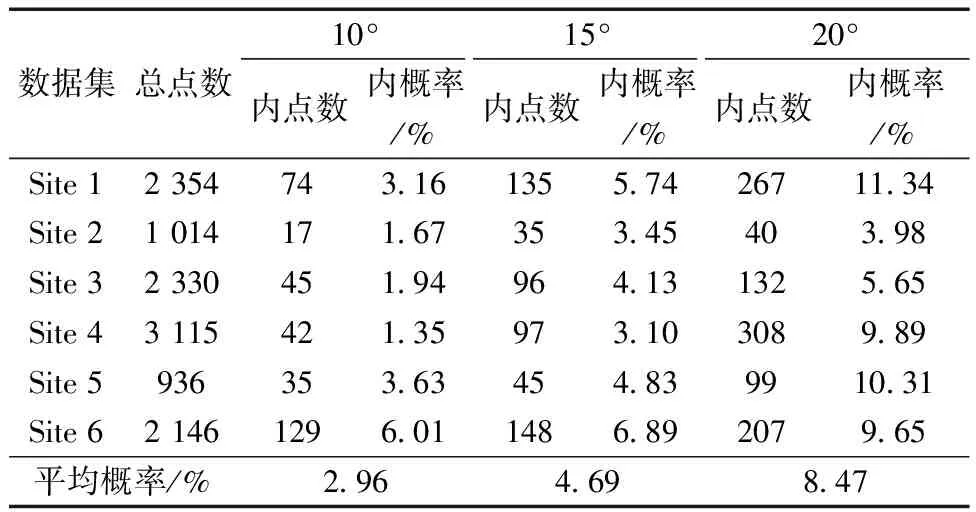
表2 植物群样本数据

1.3 基于最小二乘法的曲线拟合

鉴于在点云数据中无法通过向量夹角区分植物点和弯曲屋顶点,引入曲线拟合方法以解决该问题。建筑物屋顶点云通常具有人为设计的特征,其分布呈现规律的连续曲线,并且相邻点之间的欧氏距离存在一定规律。与此相反,植物点的点云分布通常不规则,并且相邻点之间的欧氏距离变化较大。因此,可以根据这一特点计算点间欧氏距离并依靠最小二乘法拟合曲线,根据拟合曲线的残差进行建筑物曲面屋顶的提取。

1.3.1 拟合曲线残差

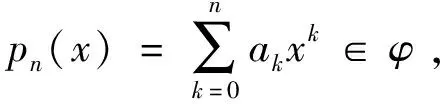
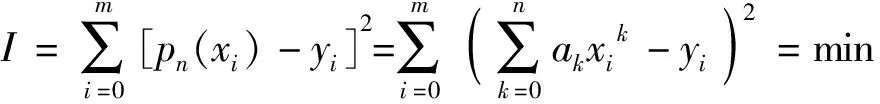
(3)

式(3)中:I为多元函数;xi、yi为二维空间的横纵坐标值;min为多元函数的最小值。

由多元函数极值的必要条件,得

(4)

式(4)的系数矩阵是一个对称正定矩阵,存在唯一解。解得ak(k=0,1,…,n)可得多项式为

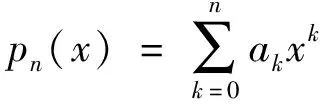
(5)

式(5)为所求的拟合多项式,称为最小二乘拟合多项式,残差的平方计算公式为

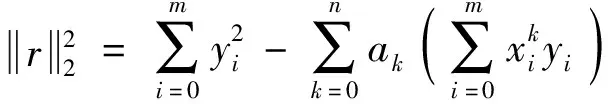
(6)

1.3.2 曲线拟合阶数及残差阈值确定

根据图8(a)所示,所研究的建筑物的屋顶呈现出具有曲率变化的曲面,并且呈现出不规则的特征,从左至右曲率逐渐增大。与此对应,图8(b)描绘了建筑物中一条扫描线上相邻点之间的欧氏距离变化情况。可以看出,相邻点之间的欧氏距离变化趋势与曲面屋顶的形态变化趋势相一致,即相邻点之间的距离逐渐增大。因此,以该建筑物作为目标样本,以探究通过欧氏距离拟合曲线的阈值。

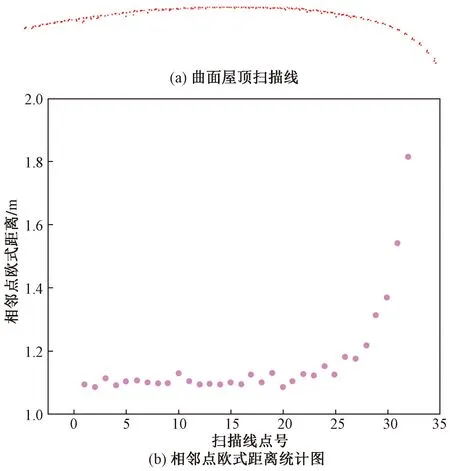
图8 建筑物样本扫描线及相邻点欧氏距离Fig.8 Scanning line of building sample and Euclidean distance of adjacent points

该建筑物样本包含扫描线共224条,以该建筑物样本的相邻点欧氏距离为样本数据,分别对每条扫描线数据建立4阶拟合曲线,5阶拟合曲线以及6阶拟合曲线,并计算每组曲线的残差。最终通过所有扫描线的残差平均值确定阈值。如图9所示,以其中一条扫描线为例,展示拟合曲线及残差的确定方式。

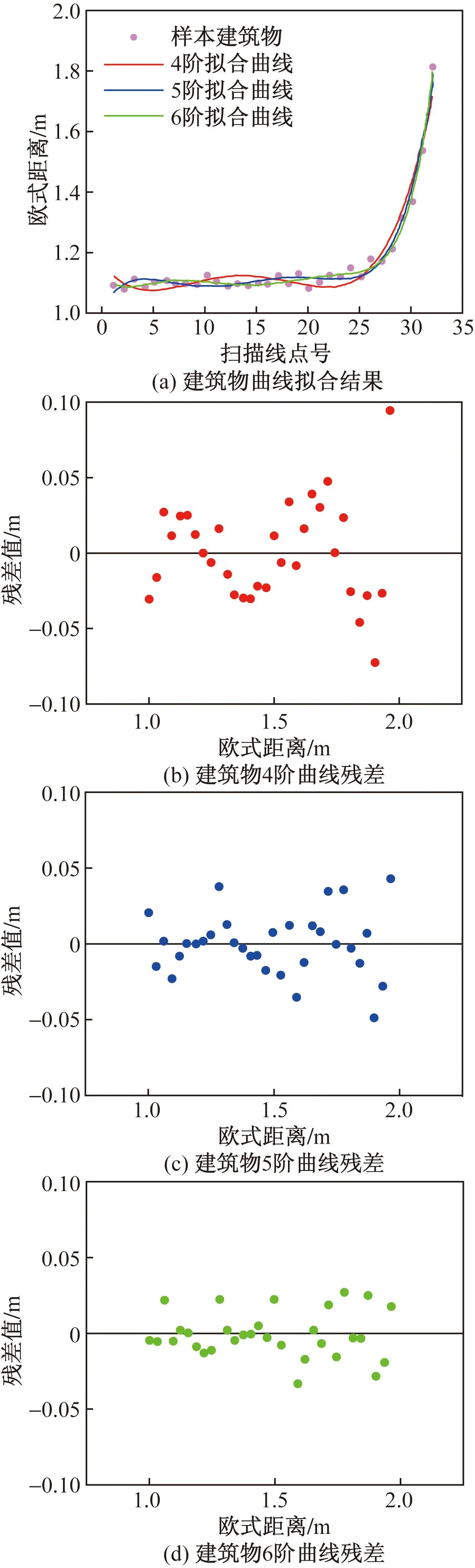
图9 建筑物样本拟合曲线及残差Fig.9 Fitting curve and residual error of building samples

图9(a)为建筑物取线拟合结果。图9(b)为该条扫描线依靠相邻点间距建立4阶拟合曲线的残差值,即曲线上的值与真实值的误差。图9(c)为5阶曲线的残差。图9(d)为6阶曲线的残差。以该条样本数据为例,4阶曲线的残差高达0.1,绝对值的平均值为0.031。5阶最大值为-0.051,绝对值平均值为0.021。6阶曲线残差的最大值为-0.043,绝对值的平均值为0.017。

用相同方法对224条建筑物扫描线计算拟合曲线以及残差,详细数据如表3所示,随着拟合曲线的阶数提升,残差值降低的趋势逐渐减缓。而224条扫描线计算总时间随着阶数的增加而快速增加。综合考虑时间成本与准确率,确定算法的拟合曲线阶数为5阶。为了确定残差的具体阈值,采用相同方法对植物样本进行实验。

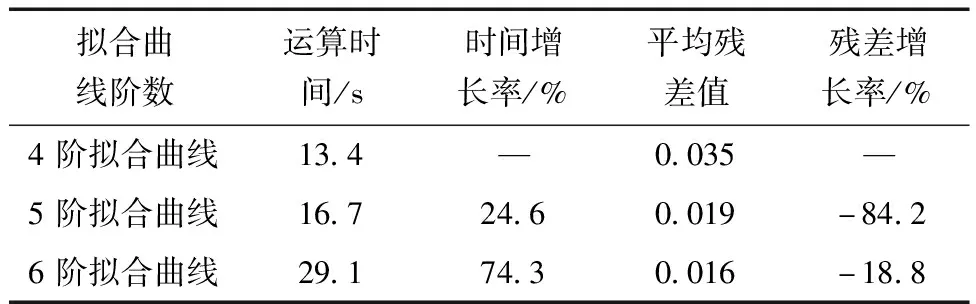
表3 建筑物样本数据

植物样本共174条扫描线,仍然以一条扫描线为例,植物样本的结果如图10所示。4阶拟合曲线的残差值极小值为-0.125,绝对值的平均值为1.836,5阶最小值为-0.373,绝对值平均值为1.358,6阶残差最小值为0.064,绝对值的平均值为1.164。统计174条植物样本扫描线的5阶拟合曲线残差值,绝对值的平均值为1.846。

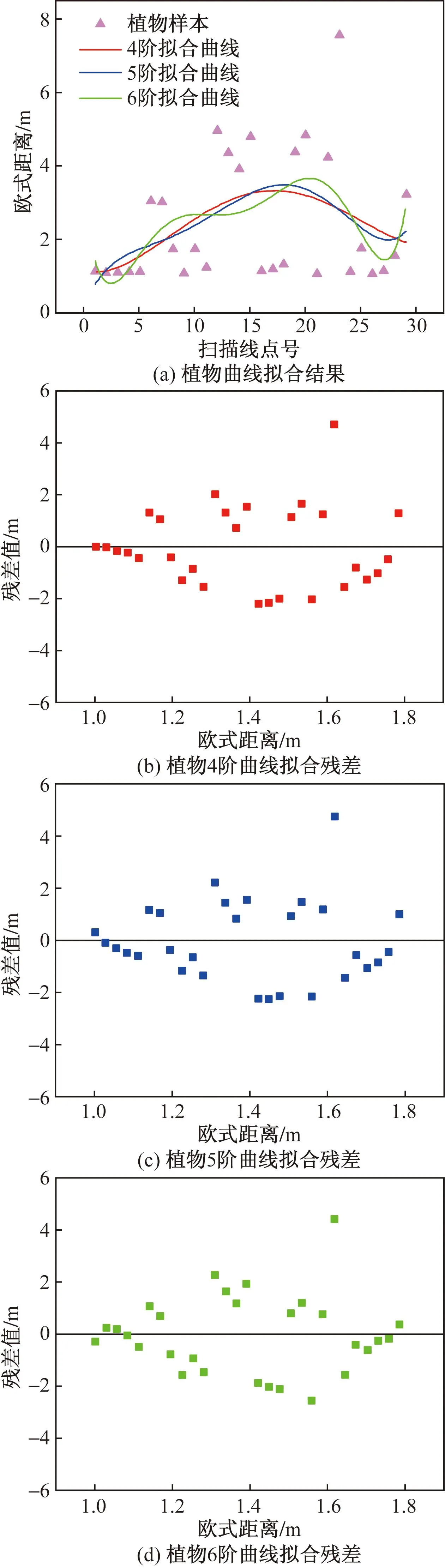
图10 植物样本拟合曲线及残差Fig.10 Fitting curve and residual error of plant samples

根据样本实验可以得出建筑物与植物的欧氏距离拟合曲线的残差值差异明显,植物样本的5阶极小值仍然明显高于建筑物残差平均值,利用正态分布原则,残差阈值采用3倍平均值即0.057。详细计算过程如图11所示。

L为初始窗口;L0为侧窗口尺度;L1为当前尺寸窗口图11 拟合曲线算法过程Fig.11 Algorithm process of curve fitting

利用拟合曲线对扫描线中的曲面提取时,需要建立窗口来提取有效的数据点。初始窗口L可以根据点的数量代替传统的距离,这意味着能够非常有效的分离出前后不连续的扫描点数据。首先,当确定L的大小时,计算当前窗口所有点间距的拟合曲线以及残差并记录;之后从窗口L的开始处进行缩减窗口并建立拟合曲线计算残差,当残差值的平均值不再减小时,固定该侧窗口尺度L0;其次,从L尾侧逐渐缩减窗口并记录拟合曲线的残差值,当残差值不再减小时,记录当前尺寸窗口L1。

根据融合向量角度差和拟合曲线法提取建筑物时,可能存在误差,其中包括少量混入建筑物点云数据的植物点和被误删的建筑物点。可以利用KD-tree搜寻法来剔除散落的植物点。建立KD-tree结构后从点云数据中随机抽取点,计算点之间平均距离d以及全局平均距离μ和标准差σ,其中d在μ±3σ之外的被认为是离散的植物点而去除。为了恢复过删除的建筑物点,一条扫描线的建筑物提取后,重新历遍这条扫描线,当两部分建筑物的距离为3σ之内时,重新提取这部分点并比较与周围建筑物点的高程,若在范围内则可以认定是过删除的建筑物点并恢复,进而提高建筑物点云提取的准确性和完整性。

2 实验分析

2.1 实验数据

实验数据通过运5飞行器搭载Leica ALS07传感器扫描得到。传感器脉冲频率159 kHz,平均飞行高度为1 080 m,总面积达1.78 km2,平均点密度为4.6个/m2。如图12所示,该数据具有典型的高建筑密度特性的城区,植物与建筑物之间距离较短,且部分植物被修剪成规则形状。

图12 原始数据Fig.12 Raw data

2.2 实验结果

建筑提取实验使用MATLAB2019b软件平台,实验计算机具有英特尔酷睿i5-8300H,2.3 GHz CPU,16.00 GB内存和64位Windows 10操作系统。

(1)去噪和滤波结果。图13为去噪和滤波的结果,滤波后点云数量为738 957。

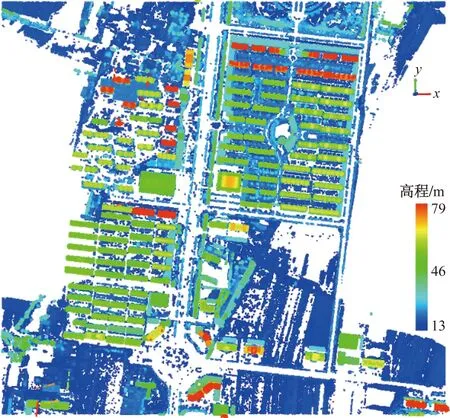
图13 滤波后结果Fig.13 Filtered results

(2)定性结果。如图14所示,将降噪和滤波后的点云作为输入点云,进行建筑物点云。图14(a)为所提算法提取结果,图14(b)为TIN算法提取结果。

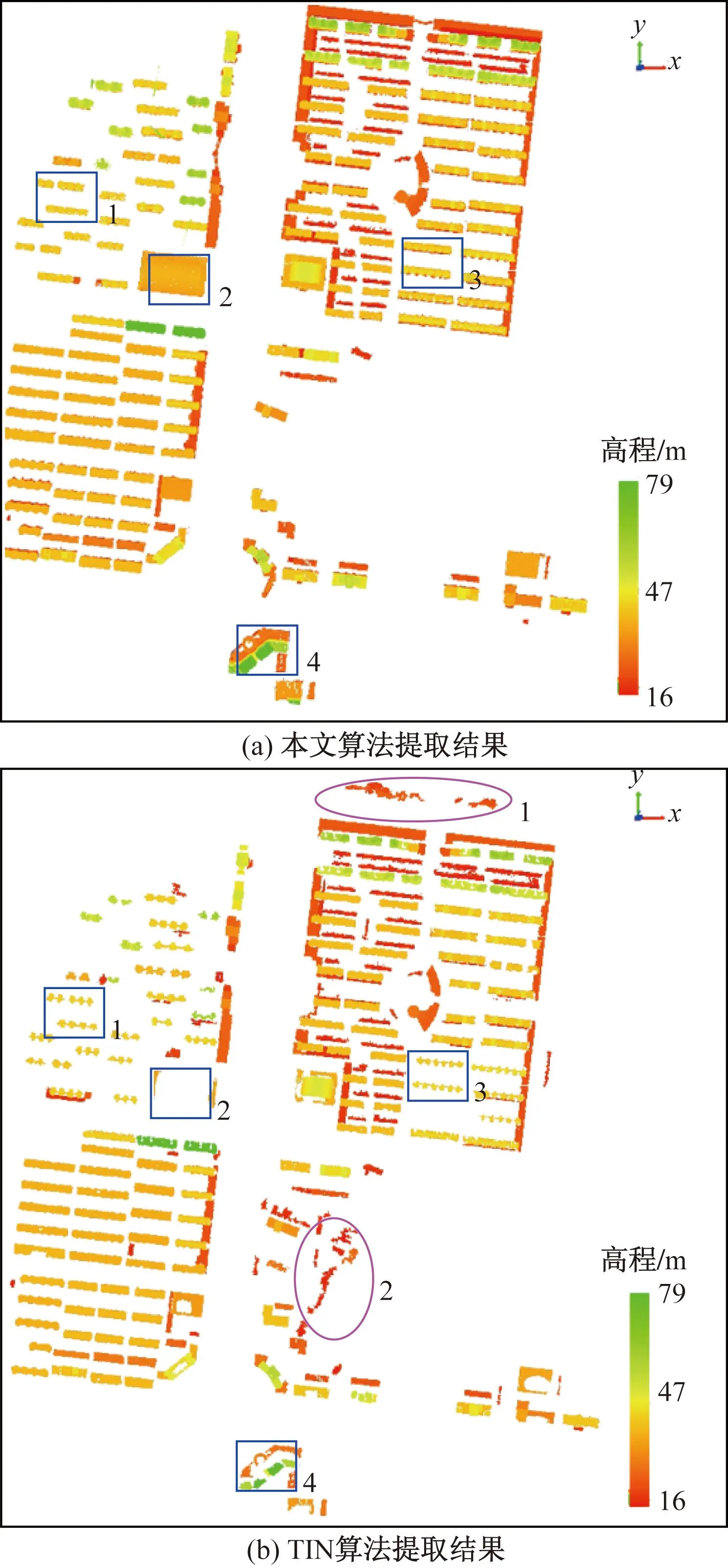
蓝色框1～4为同一区域内的不同结果;红色圆圈1和红色圆圈2为一些手动修剪后的植被图14 两种算法的建筑物提取结果Fig.14 Building extraction results of two algorithms

如图14所示,与TIN算法相比所提算法可以更加全面的提取建筑物。如图14中蓝色框1和蓝色框3所示,所提算法能够更加完整的提取边界形态复杂的建筑物。如图14中蓝色框4所示,TIN算法在面对高度变化大的平面屋顶时表现出不稳定性,不能完整提取建筑物。图14中蓝色框2为一个曲面屋顶,所提算法成功提取了整个屋顶,而TIN算法几乎漏掉了整个曲面屋顶。如图14(b)所示,红色圆圈1和红色圆圈2为一些手动修剪后的植被,在形状上表现出一定规则性,TIN算法无法有效去除这些植被。综上可知,所提算法相较于TIN算法能够更加稳健的提取平面和曲面屋顶的同时能够有效去除植被点云。

2.3 精度及效率分析

为了验证所提算法对建筑物提取的有效性,需对算法进行精度评定,采用经典模型混淆矩阵对数据结果进行评价[26]。

定义一类误差T1为把非建筑物点错误地分类为建筑物,可表示为

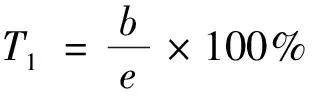
(7)

式(7)中:b为算法的建筑物数据中非建筑物点的个数;e为参考数据的建筑物点个数。

定义二类误差T2为把建筑物点错误的分类为非建筑物,可表示为

(8)

式(8)中:c为算法的非建筑物数据中建筑物点的个数;f为参考数据的非建筑物点个数。

则总误差T3可表示为

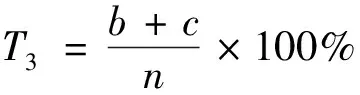
(9)

式(9)中:n为滤波后非地面点个数。

于是总体精度(overall accuracy, OA)可定义为

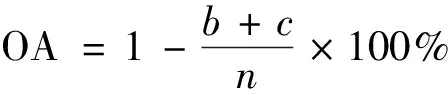
(10)

同时,为增加算法精度评价的准确性,使用kappa系数进行对算法准确性分析。

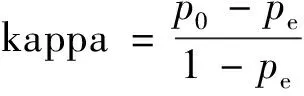
(11)

(12)

式中:p0为正确分类的建筑物点a和非建筑物点d的总和除以样本总数;pe为偶然一致性;ai为建筑物和非建筑物的真实点云数;bi为由算法分类的建筑物和非建筑物点云。

此类混淆矩阵中kappa系数替换为

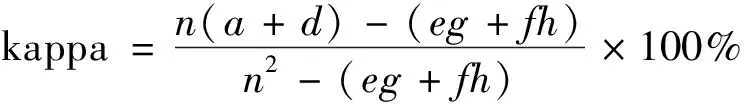
(13)

式(13)中:g为算法分类的建筑物点数;h为算法分类的非建筑物点数。

表4为3种算法在提取建筑物二元分类时的精度结果。

表4 两组实验结果精度评定

本文算法的T1为2.77%,而TIN算法的T1为7.21%。这表明本文算法在将非建筑物正确分类为负类方面表现更好,能够更加有效区分非建筑物点云。TIN算法在T2指标上略好于本文算法,但是本文算法T2也保持在较低水平,说明两种算法都能较好的识别出建筑物点云。两种方法的总体精度都高于95%,说明两种方法在整体上都具有较高的分类准确性。本文算法kappa达到了91.48%,而TIN的为87.38%。说明本文算法在不同样本上具有较高的一致性和可靠性。

与TIN算法相比,本文算法表现出更快的处理速度,TIN算法运行时间为294 s,本文算法的运行时间为118 s,仅为TIN算法的40.1%。TIN算法为了更好地提取建筑物,需要建立较多三角测量数据结构,耗时较长,而本文算法基于扫描线模型,将它将三维空间向量简化为二维方向向量,减少了冗余计算,提高了算法效率。

3 结论

提出了一种机载LiDAR建筑物点云提取方法,通过实验区数据处理,结果表明,能够有效提取建筑物点云。该算法具有以下特点:通过构建扫描线数据结构计算相邻向量角度差能够快速准确地提取平面建筑物屋顶;利用相邻点欧氏距离拟合曲线,计算残差可以准确区分曲面建筑物屋顶与植物点;最后通过细化处理能够更加完整地提取建筑物并消除植物的影响。该过程可以很好避免植物对结果的影响,同时能够非常有效的提取曲面屋顶以及高差复杂的建筑物屋顶。该算法解决了面对大面积城区建筑物复杂且植物多而提取精度不够的问题,同时能够很好提取曲面屋顶建筑物。通过成熟的TIN算法进行消融实验,验证了本文算法的有效性和稳定性。