基于能量守恒的半解析半数值多裂缝扩展模拟方法

钟安海, 鲁明晶*, 张潦源, 钱钦, 贺文君, 程呈, 朱海燕

(1.胜利油田分公司石油工程技术研究院, 东营 257000; 2.成都理工大学能源学院, 成都 610059)

水平井分段多簇压裂是开发油气资源的有效增产措施之一,研究压裂过程中水力裂缝的扩展延伸对油气的高效开采是至关重要的[1],这直接关系到油气井的产量。

为此,中外学者对多簇裂缝的竞争扩展进行了大量研究,总结出多种方法。曹楷楠等[2]结合近场动力学和有限差分法模拟了多裂缝扩展。程万等[3]采用边界元法建立了水平井多簇裂缝同步扩展模型,研究了多裂缝的竞争扩展机制。郭建春等[4]采用二维位移不连续法建立了诱导应力场分布数学模型对多裂缝扩展进行了研究。朱海燕等[5-6]基于离散裂缝方法模拟研究了页岩油藏与气藏的多裂缝扩展情况。许江文等[7]和焦战等[8]通过扩展有限元方法模拟了裂缝扩展。Dontsov等[9]提出了隐式水平集算法能够捕捉裂缝扩展的多尺度行为并定位动态移动的裂缝前缘。Cheng等[10-11]采用非线性节理单元建立流固耦合多裂缝闭合模型,对水平井分段压裂的裂缝扩展形态进行了模拟。Li等[12]扩展了基于渗透率的水平集方法(permeability-based hydraulic fracture, level set method,PHF-LSM),模拟了非均质岩层中的多簇裂缝扩展。Huang等[13]基于有限元-离散裂缝网络模型研究了工程因素对多裂缝垂向扩展的影响。Hunsweck等[14]采用有限元法,Olson等[15]采用扩展有限元法模拟了水平井中多裂缝同步扩展问题。Wu等[16]基于位移不连续法建立二维多裂缝扩展模型,模拟了水平井多簇裂缝的竞争扩展问题。上述常见的裂缝扩展数值模拟方法,都在不同程度上存在模拟精度不高或者运算效率较低的缺点,且多局限于二维尺度,难以获取水力裂缝整体形态,在模拟工程尺度下的多裂缝竞争扩展问题上具有一定的局限性。

为此,提出一种将无量纲近似解与能量守恒相结合的裂缝扩展模拟方法。该方法可充分考虑水力压裂过程中的滤失影响及多裂缝间的竞争扩展效应。在此基础上,编制半解析半数值裂缝扩展程序C5Frac,并将计算结果与ILSA II[17-18]的模拟结果进行对比验证。该方法可以实现多裂缝扩展的快速模拟,且具有极高的计算精度,能够为压裂方案设计提供实时性指导。

1 半解析半数值裂缝扩展模型

1.1 控制方程

如图1所示,水力裂缝垂直于水平井筒向前扩展。模型为单个压裂段,段长为Z,共包含N条裂缝,两两裂缝间的距离分别为hk(k=1,2,…,N-1),则可得出关系式为

图1 单个压裂段内多裂缝扩展示意图Fig.1 Schematic of multiple fractures propagation in a fracture stage

(1)

裂缝面的径向扩展由井筒处注入的不可压缩牛顿流体所驱动,并在具有渗透性的线弹性岩石中准静态延伸(即远低于岩石声速),其特征为

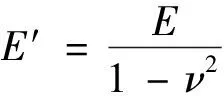
(2)

式(2)中:E为杨氏模量;ν为泊松比;E′为平面应变假设下的岩石特征参数。

韧性K′与岩石的断裂韧性KIC的关系可表示为

(3)

为简化上述问题,还需引入以下假设:①裂缝扩展遵循线弹性断裂力学;②所有裂缝面都呈径向延伸且相互平行;③重力在弹性方程和流体流动方程中均被忽略;④流体前缘与裂缝尖端重合,即不考虑流体滞后问题;⑤远场地应力均匀且恒定;⑥不考虑裂缝的扭曲和转向。

提出上述假设之后,对于每条裂缝,需要求解的未知量包括:裂缝宽度w(r,t)、缝内压力pf(r,t)、缝内体积流量q(r,t)、裂缝半径R(t)、其他裂缝施加的作用力σ(r,t)以及缝口流量Q(t)。其中,r为裂缝内某一点到裂缝中心的距离,t为时间。控制方程如下。

(1)采用卡特滤失定律描述缝内流体向地层的滤失,则缝内流体的连续性方程为

(4)

式(4)中:CL为滤失系数;k为岩石渗透性;cr为储层压缩系数;φ为岩石孔隙度;μ为流体动力黏度;σo为最小水平主应力;po为储层孔隙压力;t0为水力裂缝某处发生滤失的时刻。

(2)缝内流动方程由泊肃叶流动方程描述为

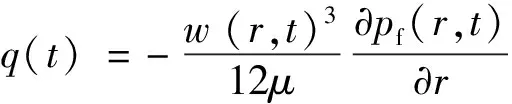
(5)

(3)通过非局部积分关系将裂缝宽度w(r,t)与牵引力T相互耦合得到裂缝的弹性方程为

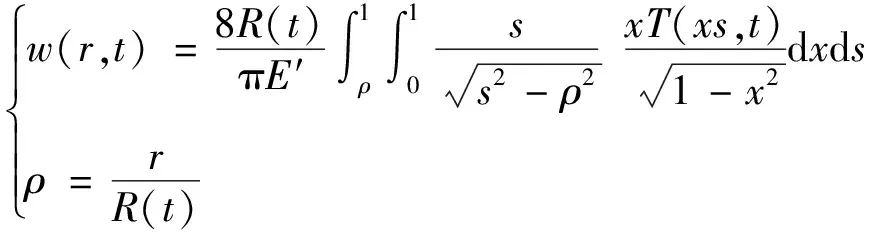
(6)

式(6)中:x和s均为裂缝内某一点到裂缝中心的距离;T为裂缝受到的牵引力,由缝内部压力、其他裂缝施加的相互作用力和远场地应力组成,其表达式为

T(ρ,t)=pf(ρR,t)-σ(ρR,t)-σo

(7)

(4)根据线弹性断裂力学,裂缝的Ⅰ型应力强度因子为[19]

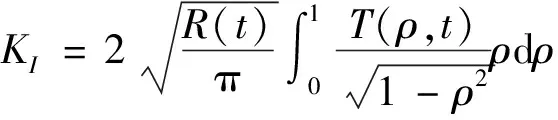
(8)

当应力强度因子达到Ⅰ型断裂韧性KIC时,裂缝即向前扩展。

(5)根据每条水力裂缝内部压力的分布,将其他裂缝施加在裂缝i上的压应力进行叠加,计算裂缝i受到的总互作用力,计算公式为

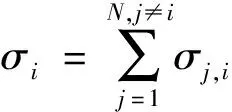
(9)

式(9)中:σi为裂缝i受到的其他裂缝叠加的总互作用力;σj,i为裂缝j对裂缝i的互作用力。

(6)假设井筒内流体流动时的压力损失为零,且流量之和等于总排量Qo,即井筒满足体积平衡。因此得

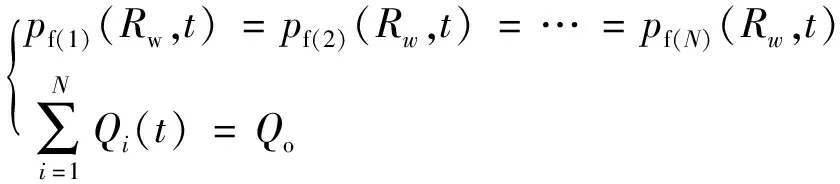
(10)

式(10)中:Rw为井筒入口半径;pf(N)为第N条裂缝的缝内压力。

因此,每条裂缝共包含:4个场方程、1个移动边界方程(裂缝扩展条件)和1个流体守恒方程。

整个系统的初始条件为

R=0,w=0,q=0,pf=0

(11)

裂缝尖端的边界条件为[20-21]

w(R,t)=0,q(R,t)=0

(12)

入口处边界条件为

2πrq(r,t)=Q

(13)

在初始和边界条件下可得到全局质量平衡方程为

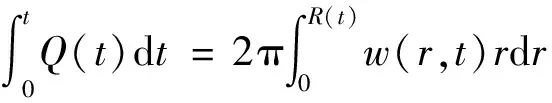
(14)

此外,还能得到雷诺润滑方程为

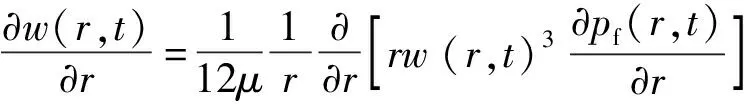
(15)

通过上述方程联立求解,确定w(r,t)、pf(r,t)、q(r,t)、R(t)、σ(r,t)和Q(t)。

1.2 近似解

1.2.1 压力分布近似解

函数形式同水力裂缝入口端和前缘附近的预期压力渐进性保持一致。压力分布函数的假设,通过消除基于流体流动控制方程的有限差分离散化来计算每个时间步上的分布需要,可大大降低计算量。通过如下方程来表达流体压力。

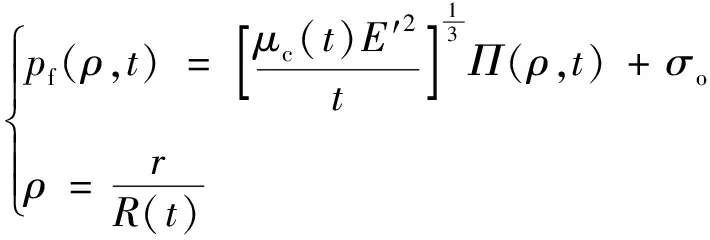
(16)

式(16)中:μc为所提出的“复合黏度”,该物理量反映滤失与韧性相关的额外能量损耗,是一个作用类似黏度的复合耗散参数;Π(ρ,t)为无量纲压力分布函数,可表示为

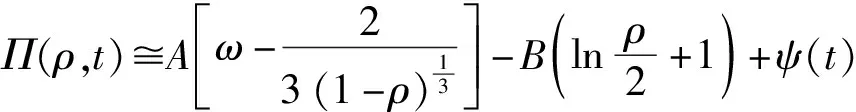
(17)

式(17)中:A、B和w为系数,在恒定泵注排量和无限均匀弹性岩石的假设下,分别取0.358 1、0.092 69和2.479;ψ(t)为空间均匀压力,与韧性相关[22]。

1.2.2 韧性近似解

裂缝扩展条件为KI=KIC,KI由牵引力T(ρ,t)计算得

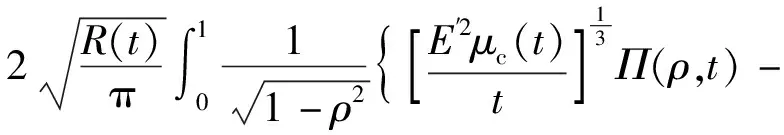
(18)

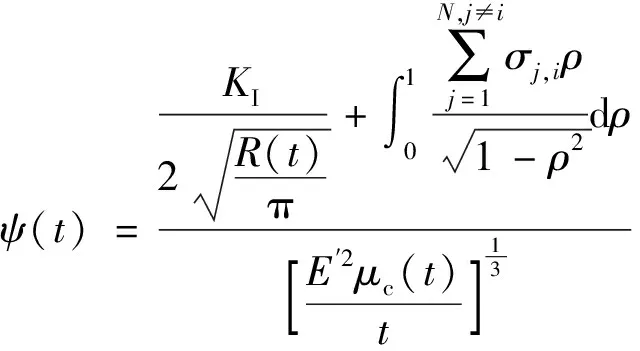
(19)

因此,式(19)提供在任何时间都满足隐式扩展的压力分布,使得复合黏度能够在每一个时间步中进行求解。并且,虽然增加了由裂缝扩展给出的新控制方程,但通过显式求解ψ(t),强制μc(t)与韧性关联,因此参与迭代的变量的数量没有发生变化。

1.2.3 相互作用力近似解

裂缝延伸时的不均匀性和瞬态压力的全弹性解是耗费计算时间的主要原因。为实现高效计算,Cheng等[23]提出一种近似方法,其中非均匀压力被均匀压力所替代,在每个时间步中为每个水力裂缝选择该均匀压力,从而产生与非均匀内压扩展出的实际水力裂缝体积相同的模拟裂缝,即

(20)

式(20)中:Pj为第j条均压裂缝引起的内部均匀静压力;wj为裂缝j的宽度。

相互作用力模型通过对所有相邻裂缝的互作用应力求和来实现。因此,施加在水力裂缝上的互作用力近似表示为

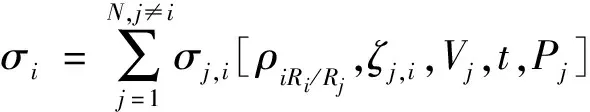
(21)

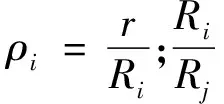
1.2.4 弹性近似解

局部裂缝宽度w(ρ,t)出现在体积平衡中,其中还包括入口边界条件中使用的入口宽度。牵引力T(ρ,t)可由式(22)给出。

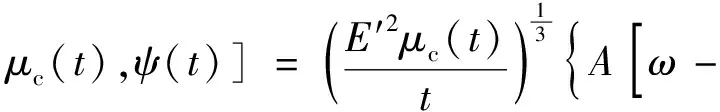
(22)

w(ρ,t)由半径r决定,将半径表示为无量纲半径γ(t)的乘积以简化运算。半径通过求解近似方程组和特征半径得

(23)

通过引入非局部弹性关系计算w(ρ,t)的所有必要变量,求解入口w(0,t)的开度。将压力代入泊肃叶方程中,得到另一个由泊肃叶定律导出的裂缝宽度。反过来,由入口边界条件得出约束限制为

(24)

1.2.5 全局体积平衡

通过对受初始和裂缝尖端边界条件影响的局部体积平衡进行积分,得到整体体积平衡方程为

(25)

式(25)中:C′L=2CL。

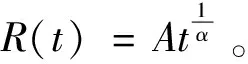
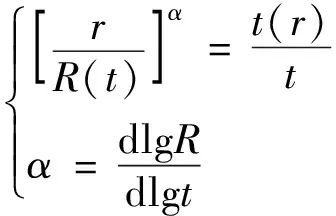
(26)

1.2.6 缝口条件

如式(10)所示,缝口条件由缝口压力等值以及井筒流量守恒给出。满足这些条件需要求出缝口压力的近似值,这将从计算得出的流体压力分布中获取。对流体压力分布进行近似估算,由于函数形式在缝口处具有奇点,计算缝口压力需要限制井筒半径,因此,解对井筒半径的敏感性往往会由于缝口附近的压力梯度较大而产生很大的误差。因此将这些入口压力视为未知数,定义它们以符合整体能量守恒。

1.3 全局能量守恒

由于井筒压力变化,很难准确估计井筒压力。因此,通过相反的近似来计算井筒的压力,以满足总能量守恒,将与韧性相关的能量添加到能量守恒式中,这使得新模型对所有的体系都有效,包括所谓的“韧性主导”体系。更新后的功率平衡为

(27)

式(27)中:pf(Rw,t)Q(t)为裂缝的能量输入速率;Dc为与岩石压裂有关的耗散率,可表示为

(28)

Df为与黏性流体流动相关的耗散率,可表示为

(29)

DL为与滤失相关的流体损失率,可表示为:

(30)

U为通过变形岩石应变能来增加应变能的一部分,是可恢复的弹性能,可表示为

(31)

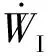
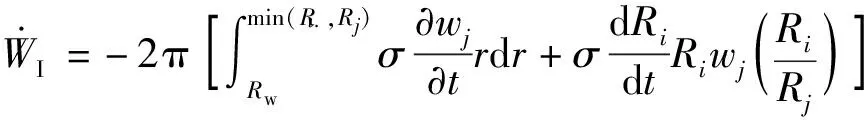
(32)

Wo为原地应力对裂缝的作用。为考虑流体损失,原位应力的功被修正为

(33)

式(33)中:S为用于量化非均匀的原位应力;α为滤失相关系数。

Pperf为通过缝口的功率损失,可通过经典压降方程[式(34)]计算。

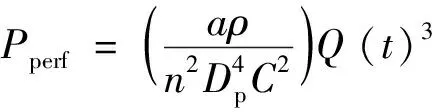
(34)

通过解压力、宽度和半径对流量的隐性依赖表达式代替未知的μc和γ得

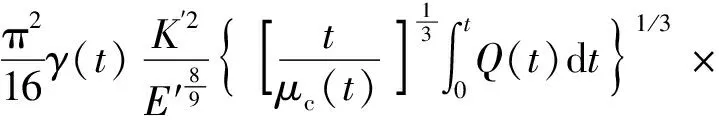
(35)

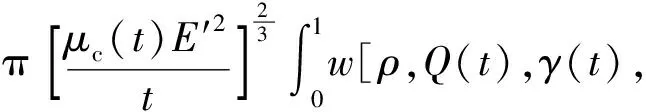
(36)

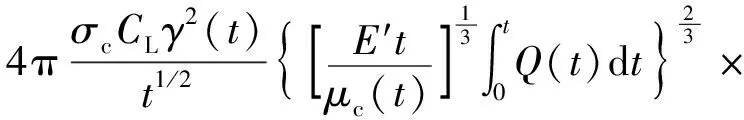
(37)

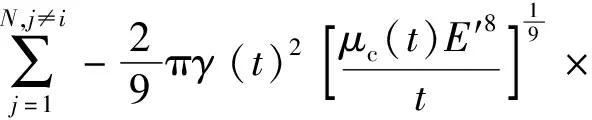
(38)

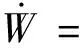
(39)

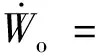
(40)

1.4 模型求解流程

求得近似解的步骤如下。

步骤1定义输入参数σc、CL、E′、μ′、KI、Qo、h。

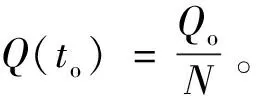
步骤3使用牛顿法求解式(24)和式(25)。

步骤4求解能量守恒方程。

步骤6将时间步长向前推进Δt,Q(t)和α(t)可作为Q(t+Δt)和α(t+Δt)的预估值。

步骤7重复步骤3～步骤6,直至达到所需的总泵送时间。

2 模型验证及计算效率对比

为验证所建立的半解析半数值方法,将该方法模拟得到的计算结果与参考解结果进行对比。根据参考解所具有的适用性,采用两类不同的参考解分别对单裂缝扩展和多裂缝扩展进行验证,并对比多裂缝扩展模拟时的计算效率。

2.1 单裂缝扩展

单裂缝扩展的参考解是由Dontsov[24]开发的一种数值近似解计算得出的。该方法可捕捉水力裂缝在低滤失与高滤失间以及高黏度与强韧性状态间的过渡行为,还可捕捉以韧性或黏度为主的水力裂缝和以滤失和存储为主的水力裂缝的扩展行为,是一种可考虑滤失的裂缝扩展高精度模拟方法。

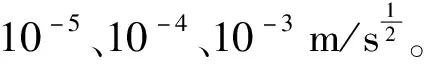
图2为C5Frac模拟结果与参考解的对比结果,可以看出,两者的误差在1%以内,同时C5Frac还可以避免近似解在滤失较大时出现的数值波动。这表明在不同的滤失系数范围下,所建立的方法均能准确捕捉裂缝尺寸和滤失程度。

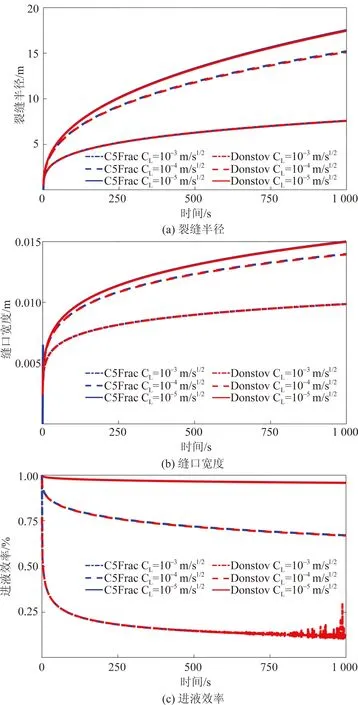
图2 C5Frac解和参考解的裂缝半径、缝口宽度和进液效率对比(单裂缝扩展验证)Fig.2 Comparison between the C5Frac solution and the reference solution in terms of fracture radius, width at fracture mouth and fluid efficiency (validation of single fracture propagation)

2.2 多裂缝扩展

在证明单裂缝扩展结果相对单裂缝参考解的准确性后,进一步验证C5Frac在模拟多裂缝扩展方面的准确性。选取ILSA II模型进行对比验证,它是ILSA[18]的扩展版本,一种基于隐式水平集算法的平面三维裂缝扩展全耦合模型[17]。ILSA II使用三维位移不连续法求解弹性方程,使用有限体积法求解流体流动。ILSA II的新颖之处在于可考虑裂缝尖端的多种渐进行为,使用隐式水平集方法追踪裂缝移动边界,即使在较粗糙的网格下仍能够获得极高的计算精度,适合作为验证多裂缝扩展的参考解。

建立的模型共包含5簇,簇间距为30 m。模型相关参数设定如表1所示。

表1 模型参数设置

图3为C5Frac和ILSA II模拟得到的多裂缝形态。可以看出,在不同的模拟时间下,两者的形态非常接近。同时,还观察到明显的应力阴影现象,外侧裂缝扩展具有优势,而内侧和中间裂缝的扩展受到抑制。

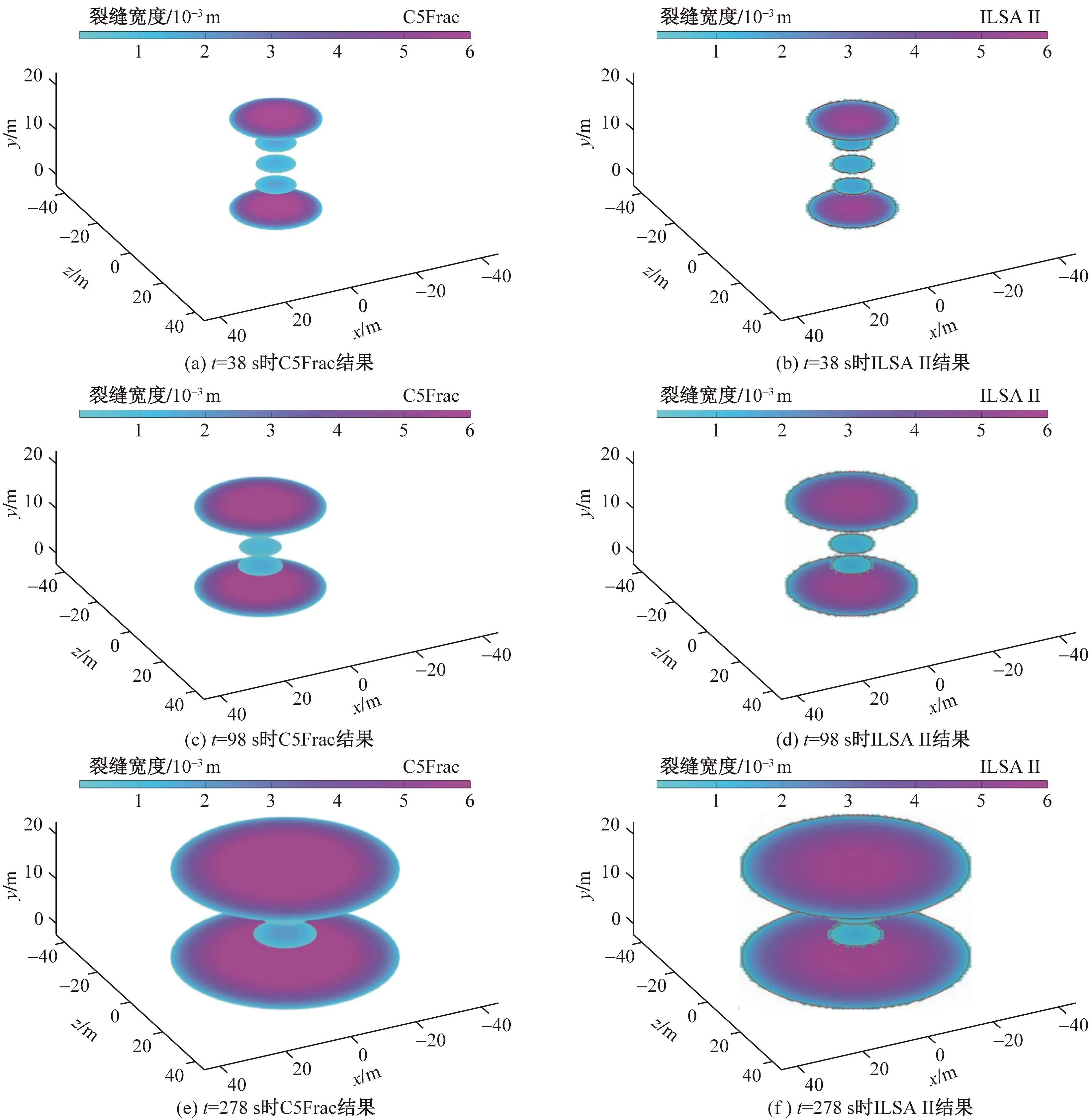
图3 C5Frac和ILSA II在不同时间下的多裂缝形态Fig.3 Geometry of multiple fractures at different time between C5Frac and ILSA II

在此基础上,进一步统计各条裂缝的相关参数进行定量对比,包括:裂缝无因次半径(裂缝半径与段长的比值),缝内流量和缝口宽度。统计结果显示,两者计算得到的无因次半径、缝内流量和缝口宽度非常接近。

从图4(b)可以看出,在模拟15 s后,泵注排量几乎全部分配给外侧裂缝,流向内侧和中间裂缝的排量降至接近零。这是因为内侧和中间裂缝在外侧裂缝产生的诱导应力场中相互竞争扩展,而内侧和中间裂缝的任何额外扩展都会增强诱导应力场。随着模拟时间的增加,外侧裂缝的扩展变得更加明显,而内侧和中间的尺寸几乎不再发生变化。上述结果表明,本文方法能够准确模拟多裂缝竞争扩展过程,且具有极高的计算精度。

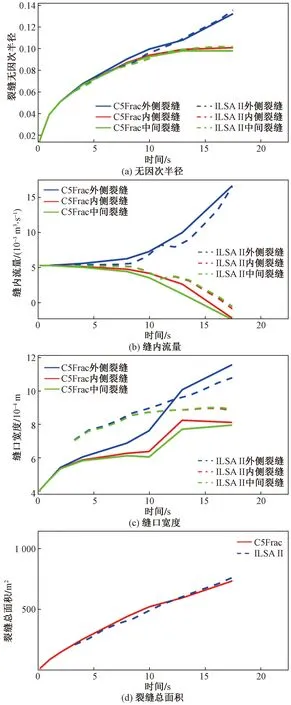
图4 C5Frac解和参考解的裂缝无因次半径、缝内流量、缝口宽度和裂缝总面积对比(多裂缝扩展验证)Fig.4. Comparison between the C5Frac solution and the reference solution in terms of dimensionless fracture radius, flow rate inside fracture, width at fracture mouth and total fracture area (validation of multiple fractures propagation)

由于压裂后单井的产能与储层改造程度高度相关,因此在统计各条裂缝参数的基础上,进一步将裂缝总面积作为评价水力压裂效果的重要指标,其定义为

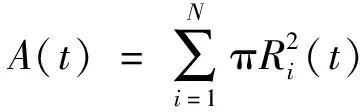
(41)

在模拟的初期,由于所有裂缝的尺寸都较小,因此它们之间的互作用力不显著,所有的裂缝都以较为接近的扩展速率增大裂缝面积,并且该过程几乎与时间呈线性关系。从图4(d)中的对比曲线可看出,ILSA II求出的总裂缝面积随时间变化的曲线与参考解的结果误差保持在5%以内,这进一步说明C5Frac模拟的准确性。

2.3 计算效率对比

随着模拟对象尺度的增加,各种需要划分网格的方法(离散元,有限元,扩展有限元)的计算时间都会大幅度增加。而本文模型不会随着模拟时间的增加降低计算速度,其在保证精度的同时所拥有的计算效率优势是现有方法中独一无二的。如表2所示,将C5Frac和ILSA II的计算时间进行对比,可以发现当模拟时间相同时,C5Frac的计算时间却远低于ILSA II,计算效率得到大幅提高。

表2 计算效率对比

3 结论

(1)将无量纲近似解与能量守恒相结合,建立一种半解析半数值的多裂缝扩展模拟新方法,并开发计算程序C5Frac。

(2)在进行单裂缝扩展模拟时,C5Frac在裂缝半径、缝口宽度和进液效率方面的计算结果与参考解的误差均在1%以内。

(3)在进行多裂缝扩展模拟时,C5Frac计算得到的裂缝半径、缝口宽度和缝内流量与ILSA II模型非常接近,裂缝总面积与ILSA II模型的误差保持在5%以内。

(4)在能够保证计算准确度的前提下,C5Frac的计算效率要远高于ILSA II,大幅减少模拟所需时间,能够更加快速高效地模拟多裂缝扩展。