压裂液滤失深度及滤失速度计算新模型

李爱芬，张环环，郭海萱，李爱山，司志梅，陈国鑫

(1.中国石油大学(华东) 石油工程学院，山东 青岛 266580； 2.中石化胜利油田分公司 石油工程技术研究院，山东 东营 257000； 3.中石化 江苏油田工程院，江苏 扬州 225100； 4.中石化 安全工程研究院， 山东 青岛 266000)

压裂液滤失深度及滤失速度计算新模型

李爱芬1，张环环1，郭海萱2，李爱山2，司志梅3，陈国鑫4

(1.中国石油大学(华东) 石油工程学院，山东 青岛 266580； 2.中石化胜利油田分公司 石油工程技术研究院，山东 东营 257000； 3.中石化 江苏油田工程院，江苏 扬州 225100； 4.中石化 安全工程研究院， 山东 青岛 266000)

建立了计算压裂液滤失深度及滤失速度的新模型，运用预处理共轭梯度法可对模型进行求解，得到压裂液的滤失深度，进而求得滤失速度。之后，应用该模型计算了滤失压差、压裂液黏度及界面张力对两者的影响。结果表明：随着压裂液黏度的减小，滤失深度与滤失速度均逐渐增大，两者与压裂液黏度呈幂指数关系；随着滤失压差的增大，滤失深度与滤失速度均逐渐增大，并与滤失压差呈线性关系；界面张力对两者几乎没有影响。

滤失深度；滤失速度；压裂液；毛细管；黏度；压差；界面张力

水力压裂工艺是有效开发页岩油藏、致密及低渗油气藏的关键技术[1-2]，压裂液滤失深度及滤失速度的大小是影响压裂设计和压裂效果的关键因素之一。国内外学者已经对压裂液滤失过程进行了大量的研究，提出了各种计算滤失速度及滤失深度的计算模型。经典滤失理论定义压裂液滤失到地层受3种机理控制[2-11]，即压裂液的黏度、油藏岩石和流体的压缩性及压裂液的造壁性，并假设滤失速度与滤失时间的平方根成反比。Economides[12]、Barre[13]等提出了依赖于裂缝净压的滤失计算方法，这些计算方法大都依托于差分方程进行计算求解。

Dr Dong等人[14-18]基于一维岩心水驱油实验提出了相互连通的毛管束模型来模拟活塞式水驱油过程，预测了水驱油前缘位置。本文建立了计算压裂液滤失深度及滤失速度的新模型，即应用毛管束模型研究压裂液驱油过程。由于压裂液及其滤液的黏度高于油相的黏度，在进行模型求解时选择了收敛性更高的预处理共轭梯度法，并分析了滤失压差、压裂液黏度及界面张力对两者的影响。

1 压裂液滤失数学模型建立与求解

实际油藏岩石中的孔隙空间多是由不规则的孔道组成的，这里将其看作由管径大小不一的相互连通的毛细管组成。在这个模型中，包括n根毛细管，其半径分别是Ri,毛细管长度为L。液体在各管中相互窜流，且同相流体相同位置处压力相等[18]。如图1所示。毛细管两端的压差Δp可以是常数，也可以随着时间发生变化。

假设在t=jΔt时刻水湿性油藏滤失前缘在各个管中的位置(如图1所示)为xi。另外，假设x≤xi时，同相流体在同一位置处的压力相等，只是距离x的函数。在定压力驱替下：

图1 简化的毛管束模型

(1)对于压裂液

第1根毛管0～x1段的滤失量可根据Hagen-Poiseuille公式

(1)

计算得到。0～x1段所有毛管的总滤失量

(2)

由此可得该段压裂液的压差

(3)

同样，xi-1～xi(i=2,3,…,n)段总滤失量

(4)

则每段压裂液的压差

(5)

(2)对于地层原油

第一根毛管x1～x2段的流量根据Hagen-Poiseuille公式

(6)

计算得到。该段地层油的压差

(7)

同样，xi～xi+1(i=2,3,…,n-1)段总流量

(8)

则每段的地层原油的压差

(9)

另外，当i=n+1时，xi=L，则

(10)

(3)辅助方程

根据毛管力公式可知毛管力[19]

(11)

定义压裂液第i根毛细管内的第j时间步的滤失速度

(12)

其中xij-1为上一时刻压裂液滤失前缘位置。

定义压裂液第i根毛细管内的第j时间步的滤失量为

(13)

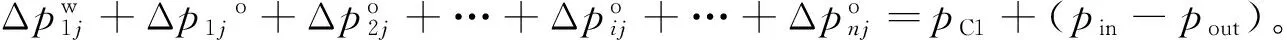
根据上述各根毛细管内各段压降及毛管力与外部压差的关系可得到一个n维二阶非线性方程组，该方程组定义了压裂液滤失的数学模型，方程组内有n个未知数xij，即第j时刻压裂液滤失前缘位置，通过预处理共轭梯度法[20-28]即可求得xij的值，进而求得滤失速度。

2 压裂液滤失深度及滤失速度影响因素

2.1 模型基础参数设置

不同渗透率的岩心其内部孔隙孔径分布不同。通过岩心压汞实验可得到孔径分布如图2所示，压汞用岩心孔隙度6.704%，渗透率0.363 5×10-3μm2,孔隙体积为0.721cm3。根据岩心压汞实验结果确定毛管半径及根数，如图3所示。毛管最大半径为1.471μm，最小半径为0.037μm，毛管长度为0.2m。压裂过程用压裂液黏度为150mPa·s，压裂液完全破胶后黏度为10mPa·s，地下原油黏度为0.83mPa·s，压裂液与原油界面张力为15mN/m。模型定压差滤失，滤失压差为4.5MPa,模型计算35min。

图2 孔隙半径分布图

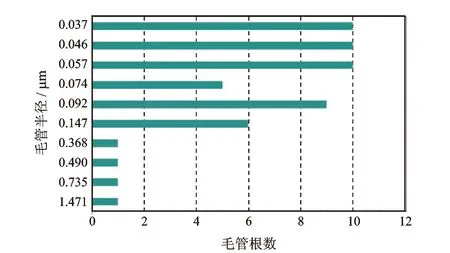
图3 毛管半径分布图

2.2 滤失压差对滤失深度及滤失速度的影响

在模型基础参数的基础上，改变滤失压差研究其对滤失深度及滤失速度的影响。模型中，忽略了滤饼引起的压差，故这里滤失压差为侵入区及油藏区的压力差。通过图4—图5可以看出，随着滤失压差与时间的增加，压裂液滤失深度增大；同一时刻，滤失压差大时滤失速度也大，但随着时间的增加，滤失速度减小。这是因为外部压力的增大增加了压裂液向地层中滤失的动力，但是同一压差下，随着时间的增加，毛管里充满了越来越多的黏度大的压裂液，毛管内黏滞阻力增大，有效滤失压差降低。在压裂施工停泵后裂缝闭合期间， 缝中的净压随着井底压力的降低而降低，所以，滤失速度也会随着缝中净压的变化而减小。由图6—图7可知，滤失深度及滤失速度与滤失压差基本呈线性关系。

图4 压差对滤失深度的影响

图5 压差对滤失速度的影响

图6 滤失深度与滤失压差的关系

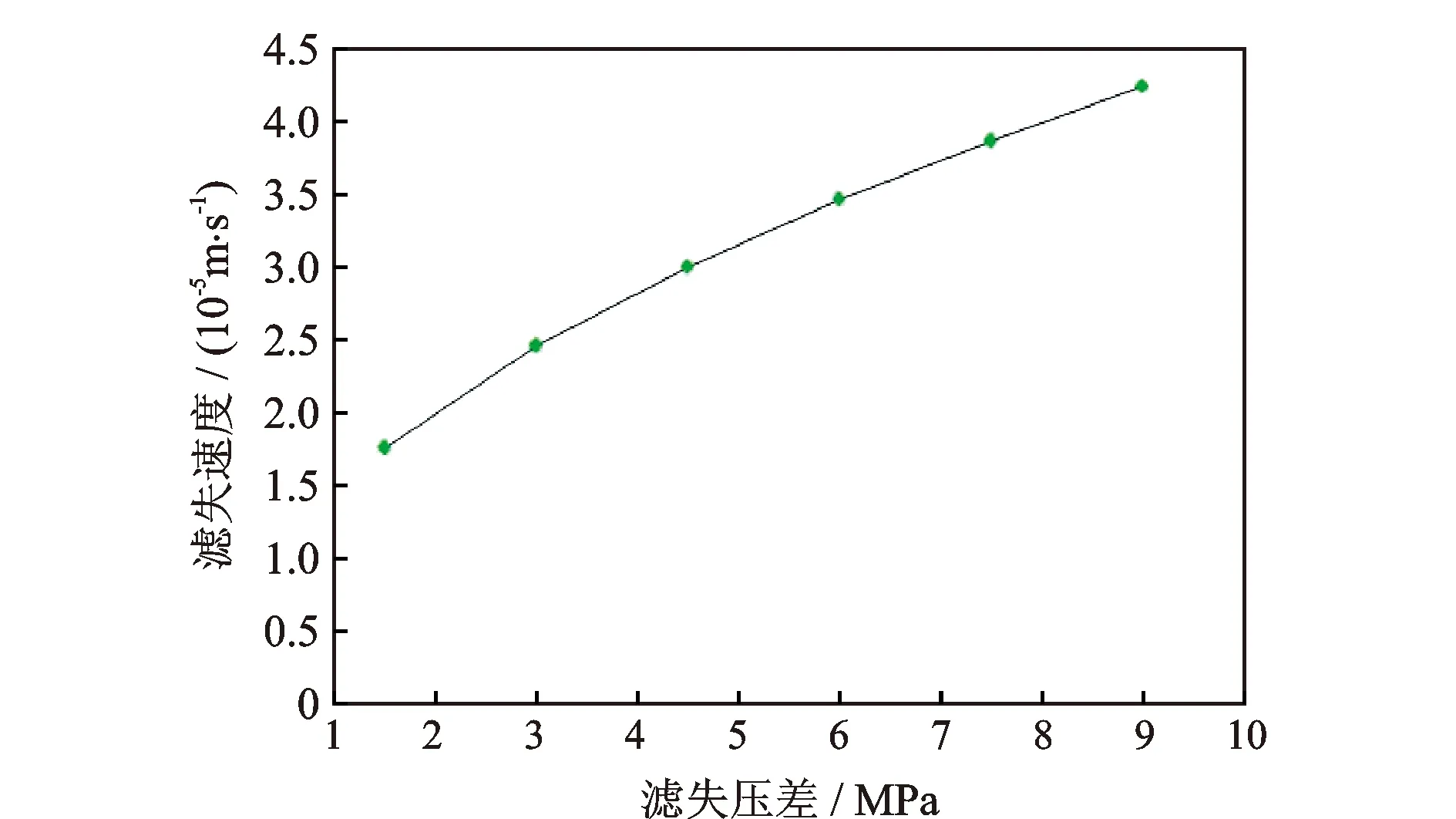
图7 滤失速度与滤失压差的关系

2.3 压裂液黏度对滤失深度及滤失速度的影响

图8—图9给出了不同压裂液黏度下压裂液滤失深度及滤失速度随时间的变化曲线。随压裂液黏度的减小，滤失深度及滤失速度均增加，这是由于黏度降低，黏滞阻力降低所致。在压裂液注入地层过程中，压裂液逐渐破胶，黏度逐渐减小，压裂滤失速度也会随之不断增加。另外，图10—图11表示第35 min时压裂液滤失深度及滤失速度与压裂液黏度的关系。从图中可以看出，滤失速度及滤失深度与压裂液黏度呈幂指数关系。

图8 压裂液黏度对滤失深度的影响

图9 压裂液黏度对滤失速度的影响

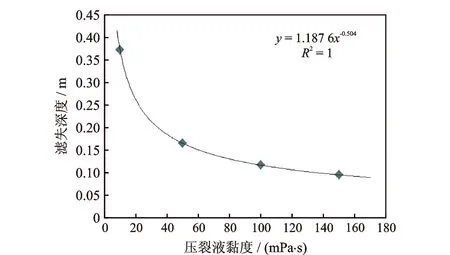
图10 滤失深度与压裂液黏度的关系

图11 滤失速度与压裂液黏度的关系

2.4 界面张力对滤失深度及滤失速度的影响

从图12中可以看出，界面张力大时，滤失深度比较大，这是因为界面张力在亲水性油藏中是压裂液滤失的动力。但是从图中也可以看出，界面张力的大小对压裂液滤失深度的影响甚微。

图12 界面张力对滤失深度的影响

3 结 论

随着时间的增加，滤失深度逐渐增大，滤失速度逐渐减小；随着滤失压差的增大，滤失深度与滤失速度均逐渐增大，并与压差呈线性关系；随着压裂液黏度的减小，滤失深度与滤失速度均逐渐增大，两者与压裂液黏度呈幂指数关系；界面张力对两者几乎没有影响。

本文模型基础数据依托于实际岩心实验结果，较以往理论计算模型更加真实可靠。简单可行的计算方法为压裂液滤失深度及滤失速度的计算提供一定的指导。

[1] 王永辉，卢拥军，李永平，等.非常规储层压裂改造技术进展及应用[J].石油学报，2012,33(s1):149-158. WANG Yong-hui,LU Yong-jun,LI Yong-ping,et al.Progress and application of hydraulic fracturing technology in unconventional reservoir[J].Acta Petrolei Sinica,2012,33(s1):149-158.

[2] Davletbaev A Y.Fluid filtration in a porous medium with wells with vertical hydraulic fracture of the formation[J].Journal of Engineering Physics and Thermophysics,2012,85(5):997-1003.

[3] 王鸿勋，张士诚.水力压裂设计数值计算方法[M].北京:石油工业出版社，1998.

[4] Economides M J.Reservoir Stimulation[M].Chichester:Wiley,2000.

[5] 曾晓慧，郭大立，王祖文，等.压裂液综合滤失系数的计算方法研究[J].西南石油学院学报：自然科学版，2005,27(5):53-56. ZENG Xiao-hui,GUO Da-li,WANG Zu-wen,et al.Study on the calculating method of the total fracturing fluid leak-off coefficient[J].Journal of Southwest Petroleum Institute:Science & Technology Edition,2005,27(5):53-56.

[6] 李勇明,郭建春,赵金洲，等.裂缝性气藏压裂液滤失模型的研究及应用[J].石油勘探与开发,2004,31(5):120-122. LI Yong-ming,GUO Jian-chun,ZHAO Jin-zhou,et al.New model for fracturing fluid leakoff in naturally fractured gas fields and its application[J].Petroleum Exploration and Development,2004,31(5):120-122.

[7] 李勇明，郭建春，赵金洲，等.裂缝性储层压裂液滤失计算模型研究[J].天然气工业，2005,25(3):99-101. LI Yong-ming,GUO Jian-chun,ZHAO Jin-zhou,et al.Model of fracturing fluid leak-off for fractured reservoirs[J].Natural Gas Industry,2005,25(3):99-101.

[8] 汪翔.裂缝闭合过程中压裂液返排机理研究与返排控制[D].廊坊:中国科学院研究生院渗流流体力学研究所，2004.

[9] Meyer B,Jacot R.Implementation of fracture calibration equations for pressure dependent leakoff[C].SPE/AAPG Western Regional Meeting,2000.

[10] Settari A.A new general model of fluid loss in hydraulic fracturing[J].Old SPE Journal,1985,25(4):491-501.

[11] McGowen J,Barree R,Conway M.Incorporating crossflow and spurt-Loss effects in filtration modeling within a fully 3D fracture-growth simulator[C].SPE Annual Technical Conference and Exhibition,1999.

[12] Fan Y,Economides M.Fracturingfluid leakoff and net pressure behavior in frac & pack stimulation[C].International Meeting on Petroleum Engineering,1995.

[13] Barree R D,Mukherjee H.Determination of pressure dependent leakoff and its effect on fracture geometry[C].SPE Annual Technical Conference and Exhibition,1996.

[14] Dong M,Zhou J.Characterization of waterflood saturation profile histories by the complete capillary number[J].Transport in Porous Media,1998,31(2):213-237.

[15] Dong M Z,Dullien F A,Dai L M,et al.Immiscible displacement in the interacting capillary bundle model(Part Ⅰ):Development of interacting capillary bundle model[J].Transport in Porous Media,2005,59:1-18.

[16] Dong M Z,Dullien F A,Dai L M,et al.Immiscible displacement in the interacting capillary bundle model(Part Ⅱ):Applications of model and comparison of interacting and non-interacting capillary bundle models[J].Transport in Porous Media,2005,00:1-16.

[17] WANG Jin-xun,DONG Ming-zhe.Trapping of the non-wetting phase in an interacting triangular tube bundle model[J].Chemical Engineering Science,2011,66(3):250-259.

[18] WANG Jin-xun,Dullien F A,DONG Ming-zhe.Fluid transfer between tubes in interacting capillary bundle models[J].Transport in Porous Media,2008,71(1):115-131.

[19] 姚军，陶军，李爱芬.利用三维随机网络模型研究油水两相流动[J].石油学报，2007,28(2):94-97,101. YAO Jun,TAO Jun,LI Ai-fen.Research on oil-water two-phase flow using 3D random network model[J].Acta Petrolei Sinica,2007,28(2):94-97,101.

[20] 李维国，同登科.数值计算方法[M].东营:石油大学出版社，2003:31-34.

[21] 柳辉.解非线性方程的牛顿迭代法及其应用[J].重庆工学院学报:自然科学版，2007,21(8):95-98. LIU Hui.Newton iteration method for nonlinear equation solutions and its application[J].Journal of Chongqing Institute of Technology:Science & Technology Edition,2007,21(8):95-98.

[22] 古发刚，任书泉.多种因素下的滤失速度计算模型[J].西南石油学院学报：自然科学版，1991,13(2):65-71. GU Fa-gang,REN Shu-quan.Model for calculation fluid-loss velocity under conditions of many factors[J].Journal of Southwest Petroleum Institute:Science & Technology Edition,1991,13(2):65-71.

[23] 罗攀，李勇明，张秦汶，等.压裂液单相滤失模型适用条件研究[J].石油地质与工程，2013,27(1):88-91. LUO Pan,LI Yong-ming,ZHANG Qin-wen,et al.Research on conditions' application of single-phase fracturing fluid filtration model[J].Petroleum Geology and Engineering,2013,27(1):88-91.

[24] 赵志红，车继明，耿彤.砂砾岩储层压裂液滤失模型研究[J].重庆科技学院学报:自然科学版，2013,15(1):76-79. ZHAO Zhi-hong,CHE Ji-ming,GENG Tong.Research on leak off model of fracturing fluid for glutenite reservoir[J].Journal of Chongqing University of Science and Technology:Natural Sciences Edition,2013,15(1):76-79.

[25] 付永强，郭建春，赵金洲，等.一种多参数的压裂液在双重介质中滤失模型的推导与计算[J].天然气工业，2003,23(3):88-91. FU Yong-qiang,GUO Jian-chun,ZHAO Jin-zhou,et al.Derivation and calculation of a multiparameter model of fracturing fluid filtration in dual porosity media[J].Natural Gas Industry,2003,23(3):88-91.

[26] 黄麒钧.扶杨油层压裂液滤失量及返排率计算[D].大庆:东北石油大学，2011.

[27] 任岚，胡永全，赵金洲，等.高渗透地层压裂液滤失模型研究[J].天然气工业，2006,26(11):116-118. REN Lan,HU Yong-quan,ZHAO Jin-zhou,et al.Research on leakoff model of fracture fluid for high-permeability reservoir[J].Natural Gas Industry,2006,26(11):116-118.

[28] 李勇明，纪禄军，郭建春，等.压裂液滤失的二维数值模拟[J].西南石油学院学报：自然科学版，2000,22(2):43-45. LI Yong-ming,JI Lu-jun,GUO Jian-chun,et al.Two dimensional numerical simulation of fracturing fluid leakoff[J].Journal of Southwest Petroleum Institute:Science & Technology Edition,2000,22(2):43-45.

责任编辑：董 瑾

2014-07-01

国家科技重大专项课题(编号：2008ZX05014-003-006HZ)资助

李爱芬(1962-)，女，博士，教授，博士生导师，主要从事油气渗流理论及提高采收率等方面的研究。 E-mail:Aifenli123@163.com

1673-064X(2015)01-0067-05

TE357.1

A