基于小波分析的油藏渗透率粗化方法

赵艳艳，李留仁

(1.中国石油化工股份有限公司 石油勘探开发研究院，北京 100083； 2.西安石油大学 石油工程学院，陕西 西安710065)

基于小波分析的油藏渗透率粗化方法

赵艳艳1，李留仁2

(1.中国石油化工股份有限公司 石油勘探开发研究院，北京 100083； 2.西安石油大学 石油工程学院，陕西 西安710065)

提出一种粗化渗透率的小波变换方法，该方法独立于边界条件并保留所有非均质信息。利用黑油模型对粗化前后油藏的动态进行了数值模拟比较，结果表明：生产10年期间，粗化后与粗化前的单元累积产油量、单元产油量、综合含水率、以及油饱和度分布等均保持较好的一致性，说明用小波变换粗化渗透率是一种较好的粗化方法，计算方便，精度高。

油藏数值模拟；储层渗透率；小波变换；粗化算法

由于现代地质学和地质统计等精细油气藏描述工具的使用，可以产生非常精细的地质模型。精细地质模型能够充分地描述油气藏的非均质性，细尺度能够控制流体在地层中的流动行为。如果用此地质模型进行油藏数值模拟，可能需要解几百万个流动方程，非常耗费机时，甚至受计算机资源限制而不能求解。因此，如何把高度细化的地质模型转变为可以进行数值模拟而不丢失油气藏的非均质信息成为一项重要的研究课题。粗化是解决这一问题的方法[1-2]。目前，油藏参数粗化的方法主要有调和平均、算术平均、几何平均、张量法[3]、空间重整化群[4]、力矩法、非参数法[5]以及有限体积法。调和平均、算术平均、几何平均方法简单，但精度较低；张量法和空间重整化群方法精度较高，但计算较复杂。另外，在石油工程和水力学中常可发现不连续点，比如：断层、裂缝和油藏岩石中地质相的变化等，以上粗化方法都会把这些不连续点进行光滑，使其弱化甚至消失[6]，并且存在对边界比较敏感等问题。本文提出一种新粗化方法——小波变换，它独立于边界条件并保留所有非均质信息，具有计算方便、精度高等优点。

1 小波变换

小波，即小区域的波，是一种特殊的长度有限、平均值为0的波形。它有2个特点：一是“小”，即在时域都具有紧支撑或近似紧支撑；二是正负交替的“波动性”。小波变换的定义是把某一被称为基本小波的函数ψ(x)(ψ(x)被叫做母小波)做平移b后，再在不同尺度a下与待分析的信号K(x)做内积。K(x)的小波变换定义为

(1)

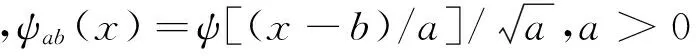
设K(x)为x点的渗透率，f(K(x))表示油藏渗透率分布，则K(x)的小波变换是在不同尺度和位置上K(x)在小波空间的表示，通过K(x)的小波变换，可在粗化的长度尺度上分析K(x)，在粗化的长度尺度上压缩f(K(x))的信息。

2 二维信号的小波变换

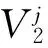
φ(x,y)=φ(x)φ(y)。

(2)

信号f(x,y)在不同分辨率下的近似，通过计算信号与尺度函数的平移和伸缩的内积求得，细节通过计算f(x,y)和二维小波函数的内积求得。如果ψ(x)是与尺度函数φ(x)相联系的一维小波，对应的二维小波为

ψ1(x,y)=φ(x)ψ(y)，

ψ2(x,y)=ψ(x)φ(y)，

ψ3(x,y)=ψ(x)ψ(y)。

(3)

φ(x,y)，ψ1(x,y)，ψ2(x,y)和ψ3(x,y)的平移和伸缩组成了L2(R2)空间中f(x,y)的整个多分辨分析空间的基函数。f(x,y)和尺度函数及小波函数的内积

Af=f(x,y)*φ(x,y)，

D1f=f(x,y)*ψ1(x,y)，

D2f=f(x,y)*ψ2(x,y)，

D3f=f(x,y)*ψ3(x,y)。

(4)

对于数据列f(x)，在分辨率2j处的近似记为Af(x)j。另外，信号在分辨率2j+1处的近似含有在较低分辨率2j计算同一信号的所有信息。从Af(x)j+1计算Af(x)j的过程称为粗化。2个连续分辨率处的近似信息的差叫做信号的细节记为Df(x)j，且

Df(x)j=Af(x)j+1-Af(x)j，

(5)

亦即

Af(x)j+1=Af(x)j+Df(x)j。

(6)

式(6)表明，高分辨率的近似可由低分辨率的近似与细节的和得到。利用小波变换的这一性质可以粗化油气藏的渗透率场，把高度细化的地质模型转变为可以进行油藏数值模拟的水平，同时不会丢失油气藏的非均质信息。

3 小波粗化结果及分析

3.1 渗透率场的粗化

经过比较，本文使用db1小波进行渗透率场的粗化。图1为原始渗透率场，它是河流相沉积形成的非均质油藏，油藏厚度为3m，粗化前网格步长为50m×40m，网格数是100×130。图2为用小波变换方法一级粗化后的渗透率场，网格数是50×65，x轴和y轴2个方向的网格步长增加了一倍，网格数减少了3/4。

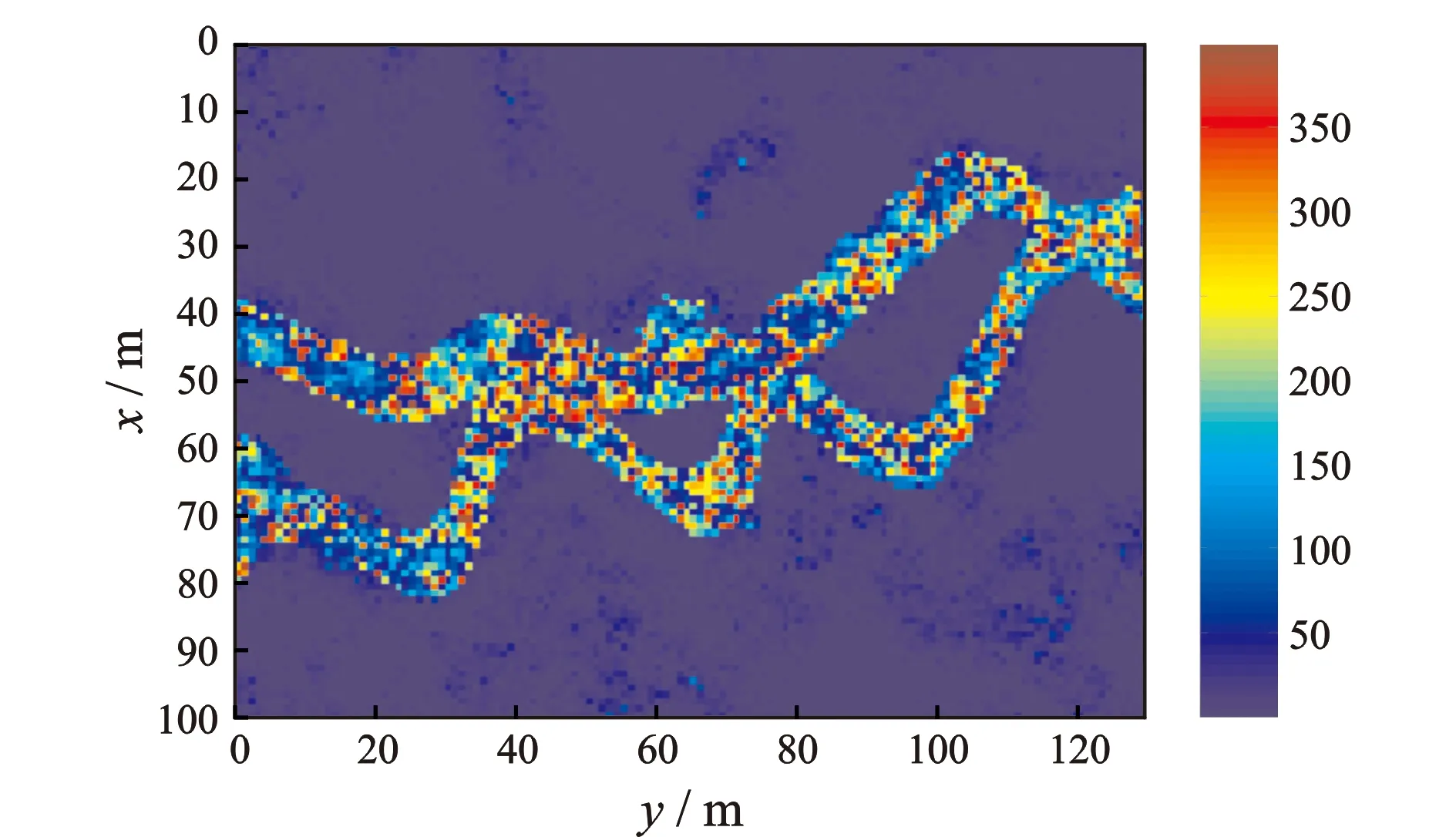
图1 原始渗透率图(网格数100×130)

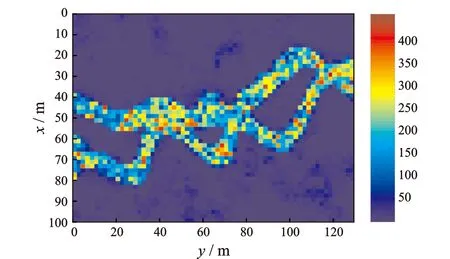
图2 小波粗化结果(网格数50×65)

3.2 粗化前后油藏开发动态数值模拟比较

对粗化前的原始渗透率场(100×130)和一级粗化后的原始渗透率场(50×65)，用黑油模型在PC机上进行10 a油藏动态预测和比较(共有6口生产井，3口注水井)，粗化前后的地层平均压力、单元累积产油量、单元油产量、综合含水率变化对比曲线分别如图3—图6所示，粗化前后的油饱和度分布如图7所示。可见，10 a期间，粗化前后的油藏动态参数极为吻合，均表现出较好的一致性。

数值模拟结果表明，小波变换是一种较好的渗透率粗化方法，在保留了渗透率场的所有非均质信息的同时，能大幅度降低计算时间，提高效率。

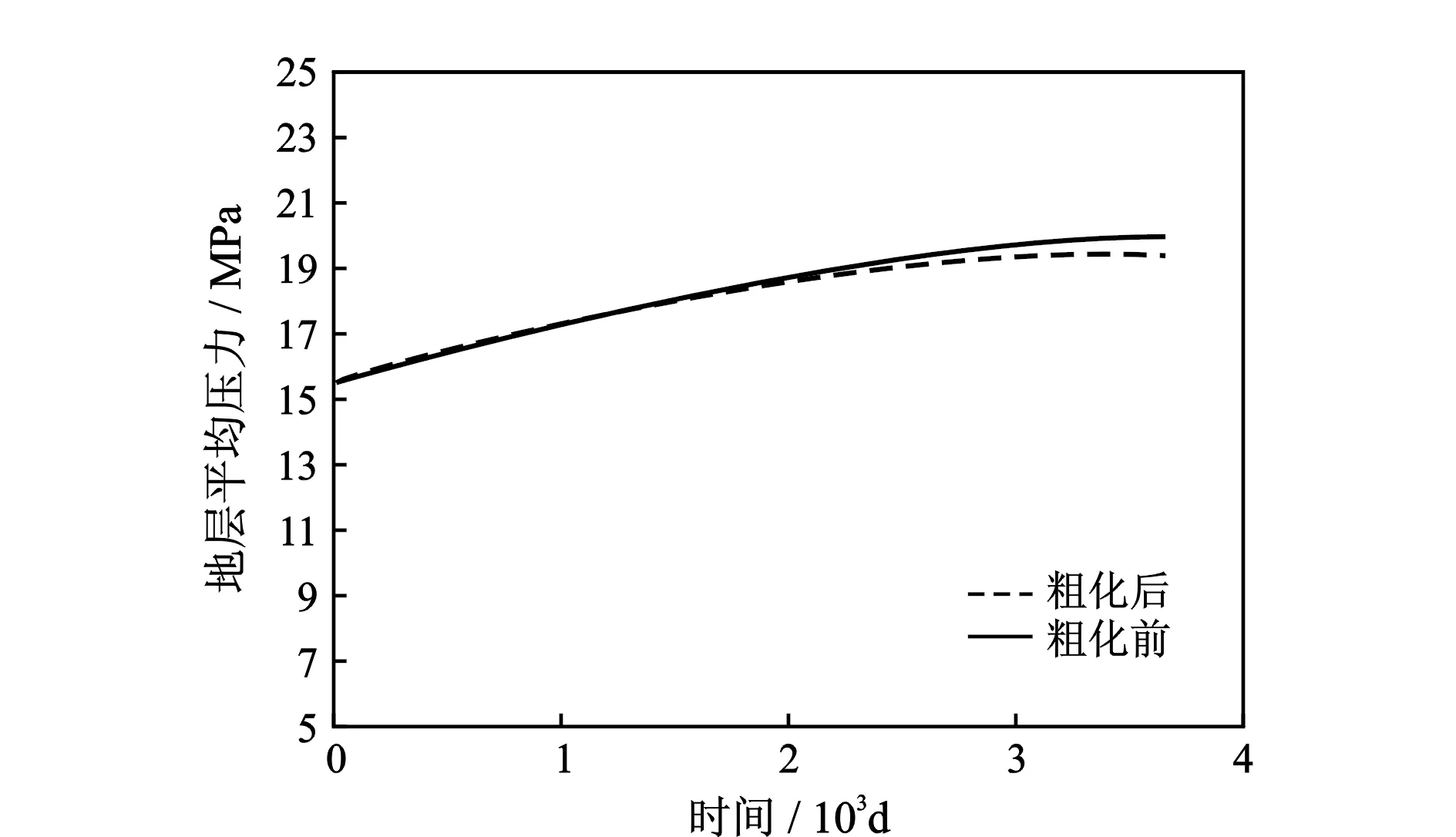
图3 地层平均压力变化曲线

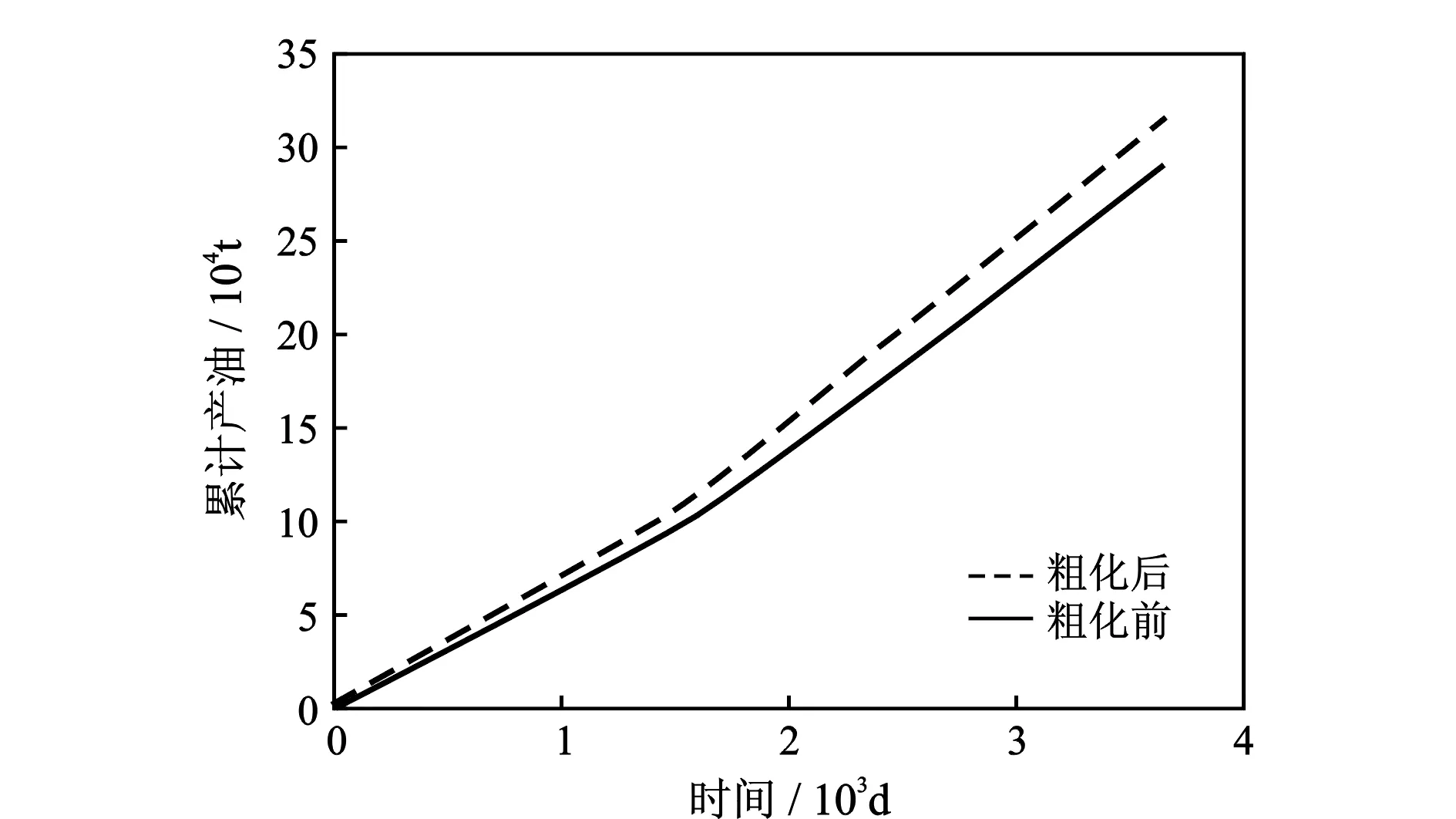
图4 单元累计产油量变化曲线

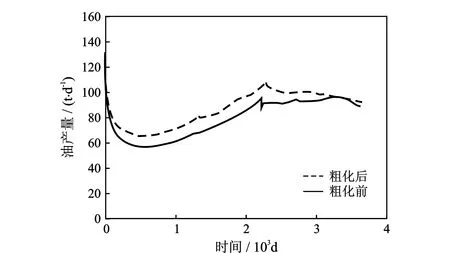
图5 单元油产量变化曲线

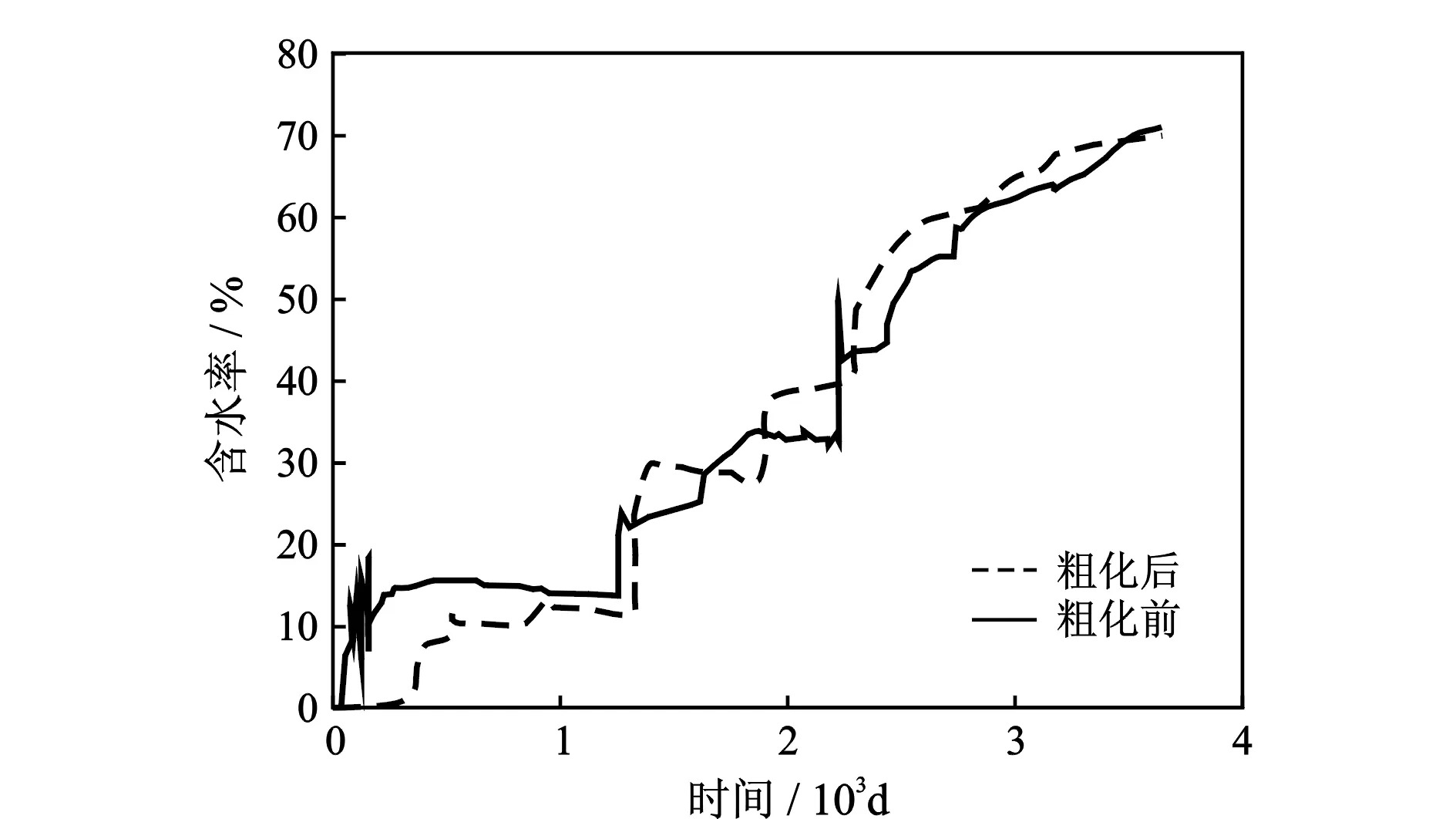
图6 综合含水率变化曲线

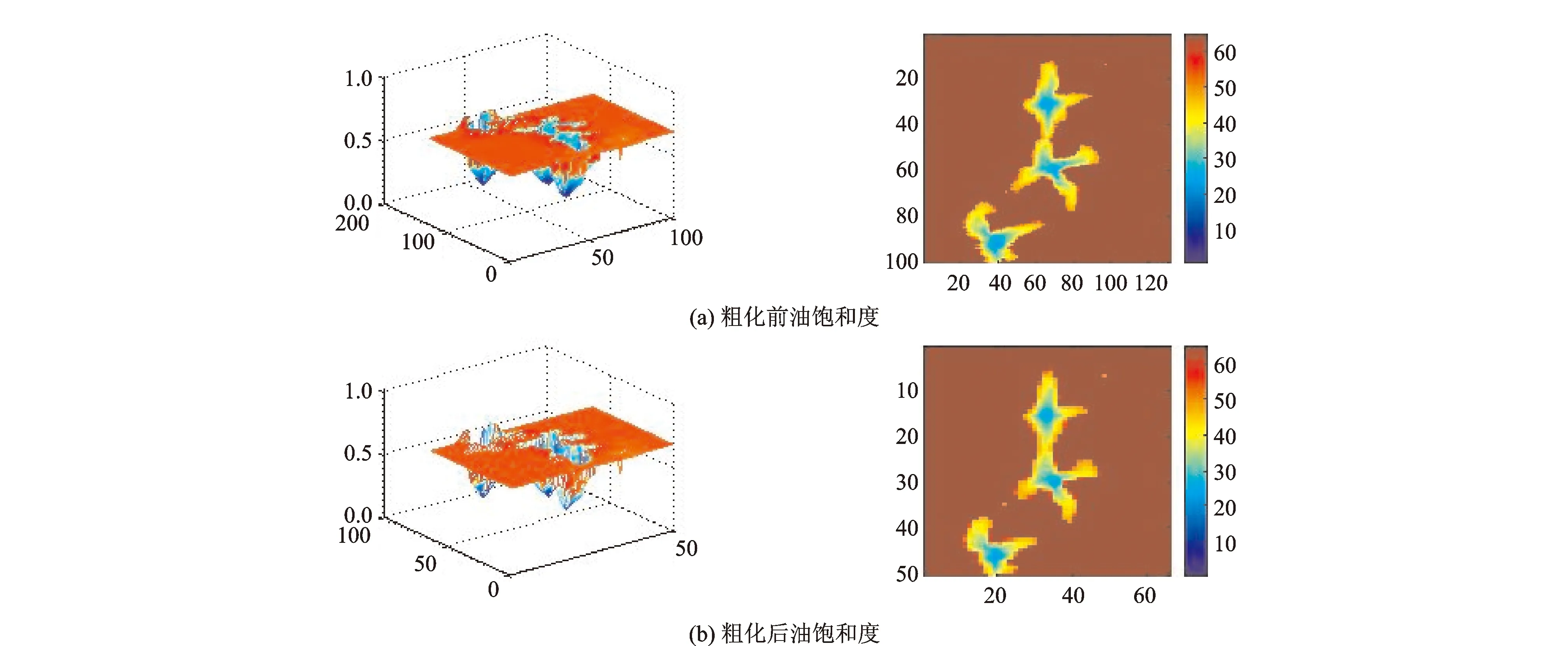
图7 生产10 a后油饱和度分布图

4 结 论

(1)与调和平均、算术平均、几何平均、张量法、空间重整化群、力矩法、非参数法和有限体积法油藏参数粗化的方法相比，本文提出的小波变换粗化渗透率方法具有独立于边界条件并保留所有非均质信息的优势。

(2)通过用黑油模型对粗化前后油藏的生产动态进行数值模拟预测对比结果表明，10 a期间，小波变换粗化后的产油量、产水量、含水率以及油饱和度分布与粗化前均保持较好的一致，说明用小波变换粗化渗透率是一种较好的粗化方法。

[1] Tawre.Apractical Approach for Assisted History Matching Using Grid Coarsening and Streamline-based Inversion:Experiences in a Giant Canbonate Reservoir[C].141606-MS SPE,2011.

[2] Lomeland Frode.A Versatile Representation of Upscaled Relative Permeability for Field Application[C].154487-MS SPE,2012.

[3] Kasap E,Lake L W.Calculating the Effective Permeability Tensor of a Gridblock[C].SPE Form Eval,1990,5(2):192-200.

[4] Kitanidis P K.Effective hydraulic conductivity for fradually varying flow[J].Water Resource,1990,26(6):1197.

[5] Dykaar B B,kitanidis P K.Determination of the effective hydraulic conductivity for heterogeneous porous media using a numerical spectral approach[J].Water Resource,1992,28(4):1155.

[6] Panda M N,Mosher C C,Chopra A K.Application of Wavelet Transforms to Reservoir Data Analysis and Scaling[C].SPE 60845,2000.

责任编辑：张新宝

2014-07-01

国家重大专项14项目05课题“复杂介质数值模拟技术与软件”(编号：2011ZX05014-005)

赵艳艳(1969-)，女，博士，主要从事油气田开发研究。E-mail:62410155522qq.com

1673-064X(2015)01-0080-03

TE319+

A