一维混合传感器阵列信号波达方向估计

胡必伟，吴志平，饶 伟，李源清，胡毕炜

（1.江西省科技基础条件平台中心，江西 南昌 330003；2.南昌工程学院信息工程学院，江西 南昌 330099）

0 引 言

一维均匀线阵（Uniform Linear Array，ULA）是阵列信号处理领域中最基础的阵列结构之一［1］，由于其容易实现的结构和良好的结构拓展性，受到了许多学者的研究。首先是一维线型标量传感器阵列，通过将多个标量传感器等间距地放置在同一条水平线上，对阵列接收信号进行数据处理就可以实现对入射信号波达方向（Direction of Arrival，DOA）的估计［2］。但是，受到奈奎斯特采样定律的影响，为了避免循环模糊相邻阵元的间距需要小于等于载波的半波长［3］，这使得阵列的孔径受到了极大的限制。同时，传统线型阵列的可识别信号个数无法超出阵元个数［4］。为了解决上述问题，人们提出了稀疏阵列结构［5］，其中包括一维嵌套阵列［6］和一维互质阵列［7］。在一维嵌套阵列中，包含有2个间距不同的子阵列，其中第1个子阵列仍然是半波长的间距排列，第2 个子阵列以多倍半波长的间距排在第1 个子阵列之后。利用嵌套结构中的2 个子阵列阵元间距不同的特点，结合嵌套阵列的协方差矩阵中元素结构和方向矩阵中元素结构的相似性，生成一个具有更多虚拟阵元和更大阵列孔径的虚拟均匀线阵。与一维嵌套阵列不同，一维互质阵列的2 个子阵列都是以不同的多倍半波长等间距穿插排列的，需要注意的是，2 个子阵列的间距之间必须是互质关系［8］。区别于一维嵌套阵列生成的虚拟阵列，一维互质阵列生成的并非是均匀的虚拟线阵，因此后续还有多种基于此的提升方法［9］。

随着声矢量传感器在阵列信号处理中的使用［10］，直接将阵列中的标量传感器替换成声矢量传感器，可以实现估计性能的提升，这种提升最直接的来源是矢量传感器阵列具有的接收信号冗余性［11］。而冗余性来源于矢量传感器的自身结构，由于单个矢量传感器是由多个传感器部件组成［12-13］，因此矢量传感器可以额外地检测到入射信号的多个维度的信息。因此，该接收信号具有天然的高维度特点，这也促使了张量代数在矢量传感器阵列信号处理中的应用［14-16］。 平行因子分解（Parallel Factorization，PARAFAC）亦称为正则多元分解（Canonical Polyadic Decomposition，CPD），Sidiropoulos等［17］首先结合CPD 提出了基于均匀线阵的DOA 估计算法。该算法将整个阵列分割成几个相同大小、空间上部分重叠的子阵。阵列接收到所有的信号可以表示为一个三阶张量，然后通过CPD 分解得到阵列信号的DOA 估计。在DOA 估计中，与估计性能直接挂钩的是阵列自由度和阵列孔径，为了提高这2 个目标参数，将矢量传感器移植到一维嵌套阵列结构［18］。同时，由于矢量传感器的引入，阵列接收信号的维度也提高了［19］，为了避免使用传统DOA 估计算法（例如传统MUSIC 算法［20］）的多维搜索带来的高成本，在使用嵌套阵列结构的同时，使用了张量代数［21］作为数据处理工具。为了充分运用矢量传感器阵列信号的多维数据结构，文献［22］使用张量代数中的张量分解实现了对均匀矢量传感器阵列入射信号波达方向的估计。相比较于声矢量传感器阵列信号处理中传统的矩阵代数算法［23］，该方法不仅降低了计算复杂度，而且带来了估计性能上的提升。为了进一步提高阵列自由度（Degree of Freedom，DOF），将电磁矢量传感器阵列的结构特点和张量代数相结合，文献［24］中使用相同的嵌套电磁矢量传感器阵列构造出了一个具有更高DOF 的张量数据模型，因此DOA 估计的精度和角度分辨率得到了进一步提高。

尽管在阵列结构中引入矢量传感器能够带来性能的提升，但是矢量传感器阵列的成本随着传感器个数的增加直线上升［25］。为了降低矢量传感器阵列的成本，或在相同的阵列成本下进一步提升信号DOA估计的性能，本文提出一种由标量传感器和声矢量传感器组成的混合传感器阵列结构。该阵列中的标量传感器和声矢量传感器分别构成了2 个阵元间距不同的ULA。然后和许多稀疏阵列信号的处理方法［5］类似，利用张量代数对这2个ULA 接收信号的互相关（即二阶统计量）进行处理，推导出2 个三阶张量数据模型，分别对应于2 个虚拟矢量传感器阵列的接收信号。根据这2 个虚拟矢量传感器阵列的空间分布特点，通过对2 个三阶张量进行切片重排，再进行合并得到一个新的三阶张量数据模型，该模型对应于一个更大的声矢量传感器均匀线阵。分析表明，当新阵列使用M2个声矢量传感器和2M2个标量传感器时，可以构造出一个虚拟的含有约2-M2个声矢量传感器的均匀线阵。最后对该模型进行张量分解得到DOA的估计值。与文献报道的方法相比，在相同的阵列成本下，新阵列以及张量代数处理方法具有更好的DOA 估计精度和更优的角度分辨率。仿真结果验证了该方法的有效性。

1 混合传感器阵列结构及其信号模型

一维线型混合传感器阵列的结构如图1 所示。不失一般性，假设阵列中所有的阵元都是沿Z轴分布的。该阵列由2个子阵列组成，分别是由M1个标量传感器组成的均匀线型阵列ULA-1，以及由M2个声矢量传感器组成的均匀线型阵列ULA-2，阵元总数为N=M1+M2。ULA-1 位于Z轴原点两侧对称分布且相邻阵元间距为信号半波长（d）。ULA-2位于Z轴的正半轴，且其第1 个阵元位于Z轴的原点处，相邻阵元间距为M1d。

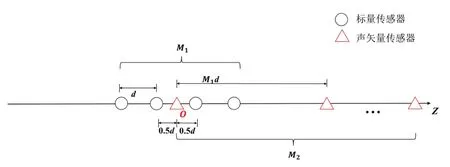
图1 一维混合传感器阵列结构

需要注意的是，一个声矢量传感器是由1 个全向压力传感器和最多3 个正交的粒子速度传感器组成［11］，其中全向压力传感器是标量传感器中的一种。在大多数传统的声矢量传感器阵列结构中，每一个阵元的位置都需要一个矢量传感器去填补。而在本阵列结构中，仅ULA-2 放置的是声矢量传感器且为稀疏分布（阵元间距为M1d），而ULA-1放置的却是标量传感器，同时声矢量传感器的个数是标量传感器个数的一半。

假设有K个具有不同方位角和俯仰角(φk，θk)，k= 1，…，K的远场窄带信号入射到本阵列中，其中方位角的取值范围是φk∈[0，π)，俯仰角的取值范围是θk∈[0，π/2)。设第k个入射信号sk的俯仰角的方向余弦为vk= sin(θk)，则由标量传感器构成的子阵列ULA-1在t时刻的接收信号向量y（1t）可表示为：

其中，w1（t）为ULA-1 子阵列对应的噪声向量，导向矢量ak= [Φ-M1/2+0.5，…，Φ-1.5，Φ-0.5，Φ0.5，Φ1.5，…，ΦM1/2-0.5]T，Φ= e-j2πvkd/λ，λ为入射信号的波长。

同理可得，由声矢量传感器构成的子阵列ULA-2在t时刻的接收信号矩阵Y2（t）为：

其中，w2（t）为ULA-2子阵列对应的噪声向量，导向矢量bk=[1，ΦM1，…，ΦM1×(M2-1)]T，pk为在原点位置的声矢量传感器对于第k个入射信号的空间响应向量［10］：

2 虚拟声矢量传感器ULA

对比式（1）和式（2）可知，声矢量传感器的引入直接导致了接收信号的数据维度的增加。为了能够高效地利用新增加的数据维度信息，接下来将采用张量代数的方法来处理一维混合传感器阵列的接收信号，以产生一个具有更多阵元的虚拟声矢量传感器ULA。

首先，与差分阵列［6］类似，为了充分利用2 个子ULA 不同的阵元间距，先求出2 个子阵信号的互相关量张量：

其中，σk为第k个入射信号的功率，a*表示取共轭，此时

观察式（4）和式（2）可知，阵列的阵元位置信息蕴藏在方向向量的相位上，即方向向量的相位差体现了该阵列的阵列结构信息。差分阵列正是利用了这一特点，先求出整个阵列的自相关数据，再将自相关数据量中表示2 个阵列方向向量进行合并并且重排，再去除重复项，就可以得到一个新的数组，新数组具有和原先子阵列方向向量类似的结构成分，但是元素个数变多了，且每个元素的相位也呈现等间距排布，这就生成了虚拟均匀线阵的方向向量。

2.1 基于阵列信号二阶统计量的虚拟ULA的构造

相比较于传统方法，新方法使用张量进行建模，区别于传统差分阵列矩阵的数据处理中单纯地拉成长矢量的方式，新方法通过张量的外积表达式来表示张量的各个组成部分，同时将张量的维度的合并和升阶处理与阵列结构的物理特征相结合，进一步地利用和开发新阵列结构潜力。利用所提出的混合传感器阵列的接收信号，构造出具有更多虚拟阵元的声矢量传感器阵列。与传统差分阵列处理方法［6］中对整个差分阵列求自相关量再进行处理的方式相比较，新方法将构造新的虚拟阵列的过程变成为2 个子阵列的二阶统计量的处理过程。

首先，将张量R1的第1维度和第3维度进行合并，得到张量R2：

然后，去除ck中的重复元素并按顺序排列，得到张量R′2：

图2 张量R′2对应的虚拟声矢量传感器均匀线阵

为了进一步增加虚拟阵列的阵元数，对张量R′2求取共轭张量，得到张量R3：

对张量R3的第1 维度中的元素顺序进行倒序排列，得到张量R′3：

与上述分析类似，张量R′3也可以被看作是一个具有M1M2个声矢量传感器ULA 的单快拍接收信号，且阵元的位置如图3所示。

图3 张量R′3对应的虚拟声矢量传感器均匀线阵

2.2 虚拟ULA的合并

为了在后续的处理步骤中，更好地增加虚拟阵列的DOF，采取将上文中2 个虚拟阵列合并的措施。因此需要对张量R3的第1维度元素进行重新排序，便于将分别位于Z轴原点左右两侧的虚拟ULA进行合并：从图2 和图3 中可以看出，这2 个虚拟线阵并非完全位于Z 轴原点的两侧，而是有一些重叠的部分。因此需要将2个虚拟ULA 重叠的部分进行舍去，也就是将张量R′2对应的虚拟线阵位于原点左侧多余的部分阵元舍弃，将张量R′3对应的虚拟线阵位于Z 轴原点右侧的多余部分舍去，再进行合并。合并时，将Z 轴原点左侧的虚拟阵列所对应的张量放在合并之后张量的前半部分，将Z 轴原点右侧的虚拟阵列所对应的张量放在合并之后张量的后半部分。

为实现上述操作，令Q是一个大小为2（M1M2-M1/2）×1的张量，且：

其表达式为：

其中，ek=[Φ-M1×M2+(M1/2+0.5),…,Φ-0.5,Φ0.5,…,ΦM1×M2-(M1/2+0.5)]T。结合上文中方向向量的特点，根据ek中元素的特征，可以看出张量Q对应于一个位于Z轴的声矢量传感器均匀线阵，并且该均匀线阵的阵元个数为（M1M2-M1/2）×2，如图4所示。

图4 合并之后的虚拟声矢量传感器均匀线阵

2.3 阵列自由度分析

如下所示，对新方法的阵列自由度进行分析。由式（10）可知，尽管此时的虚拟阵元个数得到了扩展，但是Q对应于单快拍数据。在传统的差分阵列处理过程中，需要进行矩阵域的空间平滑来实现等效快拍数的增加［6］，而本文将采用张量域的空间平滑来实现等效快拍数的增加：在进行空间平滑时将（M1M2-M1/2）×2个阵元划分为如图5所示的N个重叠子阵，且每个子阵均含有L个阵元，则有L+N=（M1M2-M1/2）×2+1成立。第n（1≤n≤N）个子阵接收信号的表达式为：

图5 空间平滑示意图

其对应的外积形式为：

其中，gk=[1，Φ，…，ΦN-1]T。根据张量H的外积表达式，可以看出，其对应于一个声矢量传感器ULA 的接收信号。其中，该阵列包括L个声矢量传感器阵元、N个等效快拍，虚拟阵元间的间距由原一维混合阵列中的间距d所决定，即半波长间距。

综上，针对所提出的由M1个标量传感器和M2个声矢量传感器构成的阵列，通过上述处理方法可得到一个具有L个声矢量传感器ULA 的N个快拍数据。接下来利用三阶张量分解的唯一性来确定L和N 的值：令k（A）表示矩阵A的Kruskal秩，张量H的分解唯一性条件为［12］：

其中，E=[e1,…,eK]、G=[g1,…,gK]和P=[p1,…,pK]称为因子矩阵。

假设入射信号的二维角度值满足文献［26］的定理4，那么各个因子矩阵的Kruskal秩与其维度存在着如下约束：

因此，结合张量分解唯一性的条件，可以得到入射信号个数K与各个因子矩阵的不同维度之间的不等式：

根据上文所述，L和N还存在着约束关系，即L+N=（M1M2-M1/2）×2+1。使用Lagrange 乘子法，将入射信号个数K的条件约束最大化问题转化为无条件约束最大化问题，从而得到入射信号个数与实际传感器个数M1和M2的关系：

根据Lagrange 乘子法易知，当L=N+1=M1M2-M1/2+1或N=L+1=M1M2-M1/2+1时，K取最大值：

因此，该虚拟声矢量传感器ULA 的自由度约为M1M2-M1/2+1。

关于阵列结构（图1）中标量传感器个数M1和矢量传感器个数M2的取值问题，参考一维嵌套阵列结构［6］并结合自身阵列结构特点，可简单将它们设置成：

综上所述，按照图1 的方式构造混合传感器阵列，其中包含M2个声矢量传感器和2M2个标量传感器。通过上述方法对该阵列接收信号进行处理后，可得到一个包含了约2-M2个声矢量传感器ULA 的约2-M2个快拍数据。显然生成的虚拟ULA中含有的阵元总数（即2-个声矢量传感器）远多于物理阵列中的阵元总数（即M2个声矢量传感器和2M2个标量传感器）。换言之，用M2个声矢量传感器和2M2个标量传感器的“阵列代价”，获得了一个包含有2-M2个声矢量传感器的ULA。

3 DOA估计

根据虚拟ULA 信号的张量模型H的表达式，可以看出入射信号的DOA 信息同时存在于不同的维度中，利用张量分解可以同时得到各个因子矩阵［12］。设因子矩阵P的估计值为P̂，P̂中的第k列表示为P̂(：，k)，P̂中的第1 行第k列的元素表示为P̂(1，k)，则通过下式可以得到入射信号的DOA估计值：

其中，和分别是方位角φ和俯仰角θ的方向余弦估计值。

同时，俯仰角θ也可以从因子矩阵E中得到入射信号的DOA 估计值：首先需要使用范德蒙恢复［12］得到因子矩阵E中每一列中元素对应的基础相位信息w（k），k=1，…，K，再根据导向矢量的表达式倒推出入射信号的角度，表达式如下：

需要注意的是，虽然一维虚拟声矢量传感器ULA可以同时估计出方位角和俯仰角，但其只在一个方向（图1 所示为Z轴方向）上有阵列孔径，该孔径对应着俯仰角。因此只从声矢量传感器空间响应维度P选取方位角的估计值，而俯仰角的估计值则从虚拟阵列的方向矩阵E中得到。

4 仿真实验

为了验证本文方法的性能，将其与文献［14，19］中的方法进行计算机仿真对比，同时将设置了6 个电磁矢量传感器的均匀线阵张量代数方法作为参考，这3 种对比方法分别简称为NS EMVS Tensor MUSIC、NS EMVS CPD、EMVS CPD。注意到这3 种对比方法均为电磁矢量传感器阵列，为了能在“相同的阵列代价”的前提下进行算法性能对比，简单起见，本文将一个标量传感器看作是1 个“部件”，一个声矢量传感器则看作含有4 个“部件”，而一个电磁矢量传感器则看作含有6 个“部件”。因此，接下来的对比实验将在各方法中所含有的“部件”数相同的情况下展开，且蒙特卡洛仿真次数均为100次。

实验1不同信噪比下DOA估计性能比较。

假设有一个远场窄带信号(φk，θk)=(27∘，65∘)入射到所有阵列中。设NS EMVS Tensor MUSIC、NS EMVS CPD 和EMVS CPD 均含有6 个电磁矢量传感器，即对应36 个“部件”。相应地，将混合传感器阵列设置成含有12个标量传感器和6个声矢量传感器，也对应36 个“部件”。将快拍数固定为1000，信噪比SNR 从-5 dB 变化到20 dB。所有方法的DOA 估计的均方根误差（Root Mean Square Error，RMSE）［27］值如图6 所示。可以看出，在传感器部件总数相同的情况下，本文所提出的混合传感器阵列具有更好的DOA 估计性能。这是因为，在传感器部件总数相同的情况下，混合传感器阵列所生成的虚拟声矢量传感器ULA具有更多的阵元和更大的阵列孔径。

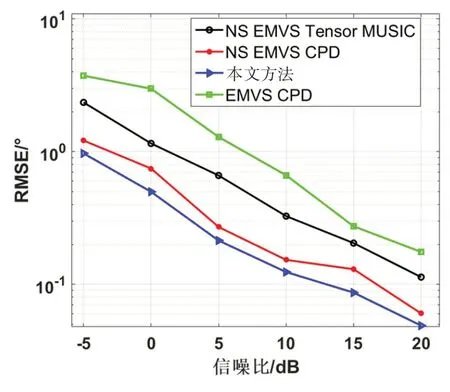
图6 RMSE随信噪比变化情况

实验2不同快拍数下DOA估计性能比较。

固定信噪比为10 dB，快拍数从100 变化到800，其它参数设置与实验1 相同。所有方法的DOA 估计的RMSE 值如图7 所示。可以看出，本文方法仍然具有最小的RMSE值，其原因与实验1中相同。

图7 RMSE随快拍数变化情况

实验3角度分辨率性能比较。

假设有2 个波达角接近的入射信号（φ1，θ1）=（15°，18°）和（φ2，θ2）=（13°，20°），将信噪比和快拍数固定为10 dB 和500，其它参数设置与实验1 相同。图8~图11 展示了所有方法的DOA 估计结果。从结果图中可以看出本文方法能正确识别出这2 个信号，NS EMVS Tensor MUSIC 识别性能略差，而其它2 种对比方法无法识别出这2 个信号。可见，由于本文方法在相同传感器部件的情况下具有更大的阵列孔径，因此在角度分辨率上存在明显的优势。

图8 本文方法的角度分辨结果

图9 NS EMVS CPD的角度分辨结果

图10 NS EMVS Tensor MUSIC 的角度分辨结果

图11 EMVS CPD的角度分辨结果

5 结束语

本文提出了一种一维混合传感器阵列结构及其相应的张量处理方法。分析结果表明，本文方法在使用M2个声矢量传感器和2M2个标量传感器的“阵列成本”下，可获得一个包含有2M22-M2个声矢量传感器的ULA，从而获得了更多的阵列自由度和更大的阵列孔径。仿真实验结果也验证了在相同阵列成本下，本文方法具有更高的DOA估计精度及更优的角度分辨率。