立体几何垂直证明思路探究

王恩泽

吉林师范大学数学与计算机学院

立体几何的垂直证明问题可以分为三类,分别是直线与直线、直线与平面、平面与平面.核心分析思路是通过假设待证的结论成立,然后结合已知条件,再进行逆向推理,得到关键信息,从而完成证明.

1 直线与平面垂直证明思路探究

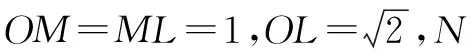
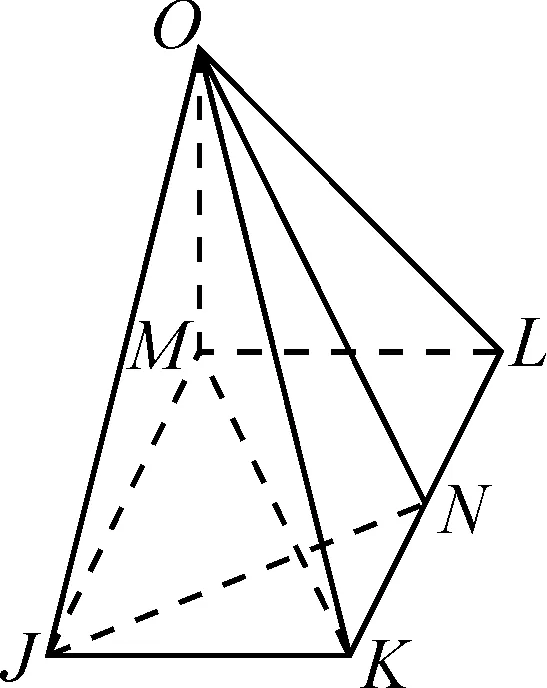
图1

证明：∵JN⊥平面OMK,

∴JN⊥OM.

∴OM2+LM2=OL2.

∴OM⊥ML.

∵OM⊥JN,OM⊥ML,直线JN与ML都在平面JKLM内且相交,

∴OM⊥平面JKLM.

思路：例1中证明垂直的方法为利用直线与平面垂直的判定定理,把直线与平面的垂直证明转化为直线与平面内两条相交直线的垂直证明.

启示:学生在立体几何主题学习过程中,要精准识记相关定理与公式,准确把握相关定理的核心内容与本质.教师在教学过程中要注意引导学生深刻理解相关概念与定理,把学过的旧知识与新知识进行串联,增强新旧知识之间的联系,帮助学生构建知识体系.

2 直线与直线垂直证明思路探究

例2如图2,直三棱柱HJK-MNO的侧面HKOM为正方形,HK=JK=2,I,L分别为HJ和JN的中点,P为棱MO上的点,LK⊥MO.证明:LK⊥PI.

图2

分析：把异面直线的垂直证明转化为直线与平面的垂直证明.先假设结论KL⊥PI成立,然后结合条件KL⊥MO进行逆推,发现两条直线正好相交于点P,所以把待证明的线线垂直问题转化为KL垂直于PI与MO所在平面的线面垂直问题,最后通过直线与平面垂直的性质定理得出待证明问题KL⊥PI.

证明：设KJ的中点为Q,连接MI,IQ,QO,PL,如图3,则直线MO,IP均在平面MIQO内.

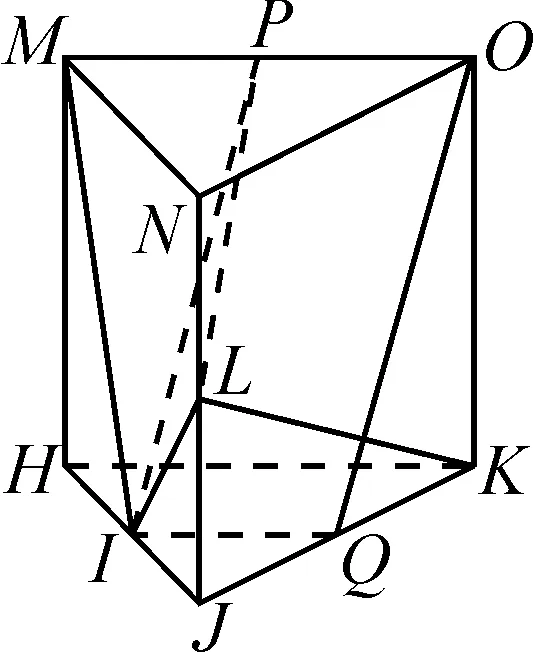
图3

∵直三棱柱HKJ-MON中,侧面HMOK为正方形,

∴HK=KJ=KO=JN=2.

∵L,Q分别为JN,KJ的中点,

∴JL=KQ=1.

又∠NJK=∠JKO=90°,

∴△KJL≌△OKQ.

∴∠QOK=∠LKJ.

∵∠LKJ+∠OKL=90°,

∴∠QOK+∠OKL=90°.

∴KL⊥OQ.

又KL⊥MO,MO和OQ在平面MOQI内相交,

∴KL⊥平面MOQI.

∵PI⊂平面MOQI,

∴KL⊥PI.

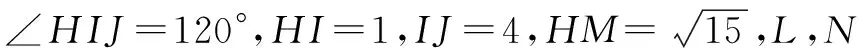
图4

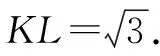
∴KJ2+KL2=LJ2.

∴∠JKL=90°,即JK⊥KL.

∵HI∥KJ,

∴HI⊥KL.

∵HI∥KJ,MK⊥KJ,

∴HI⊥MK.

∴HI⊥平面MKL.

∴HI⊥ML.

思路：直线与直线的垂直证明问题按照两条直线是否共面可分为共面直线垂直和异面直线垂直.异面直线的垂直证明比共面直线的垂直证明略显复杂,既可以把异面直线转化为共面直线后再证明垂直,又可以把异面直线的垂直证明转化为直线与平面的垂直证明.后者的思路是假设待证明的问题成立,通过将待证问题与题干中给出的垂直条件相结合,把直线与直线的垂直证明问题转化为直线与平面的垂直证明问题解答即可.

启示:学生在立体几何主题学习过程中应该合理运用逆向思维,把待证结论变为已知条件合理加以使用,改变从条件到结论的思维定势.教师在教学过程中注意合理引导学生理解并掌握逆向思维方式,提升思维的广度.

3 平面与平面垂直证明思路探究

例4如图5,四面体HIJK中,HK⊥KJ,HK=KJ,∠HKI=∠IKJ,L为HJ的中点.证明:平面ILK⊥平面HJK.

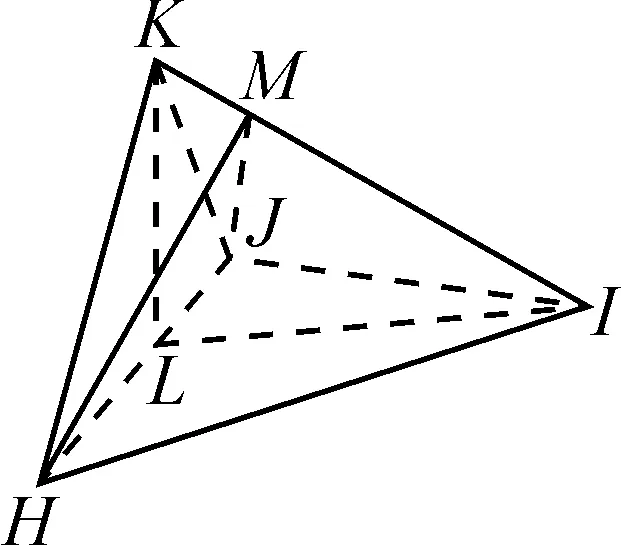
图5

分析：利用两个平面垂直的判定定理,需要在其中一个平面内找到一条与另外一个平面垂直的直线.题干给出了HK=JK,L为HJ中点,利用等腰三角形的性质可知KL⊥HJ,又因为∠HKI和∠IKJ相等,所以三角形HKI和三角形JKI全等,可知三角形HIJ为等腰三角形,则IL与HJ垂直.再证明HJ与平面ILK垂直,即可证明平面HJK与平面ILK垂直.

证明：∵在△HKJ中,HK=JK,HL=LJ,

∴KL⊥HJ.

∵∠HKI=∠IKJ,

∴△HKI≌△JKI.

∴HI=IJ.

∴IL⊥HJ.

又KL,IL都在平面IKL内且相交,

∴HJ⊥平面IKL.

又HJ⊂平面HJK,

∴平面HJK⊥平面IKL.

思路：平面与平面垂直的具体证明方法是在其中一个平面内找到一条直线与另一个平面垂直,把面面垂直问题转化为线面垂直问题,然后利用线面垂直证明思路完成证明.

启示:学生在立体几何主题学习过程中应该学会总结各种方法之间的联系,理解不同方法间的共性.教师在教学过程中应该总结提炼每种方法的精华之处,帮助学生搭建桥梁,建立全面完整的知识系统.

在高中数学学习过程中,立体几何主题是重难点[1].学生在学习立体几何主题时,应该精准识记相关定理与公式,准确把握相关定理的核心内容与本质,合理运用逆向思维,把待证结论变为已知条件合理分析,改变从条件到结论的思维定势,养成逆向思考的方式,总结各种方法之间的联系,理解不同方法间的共性.教师应在教学过程中注意引导学生主动思考[2],深刻理解相关概念与定理,把学过的旧知识与新知识进行串联,增强新旧知识之间的联系;合理引导学生理解并掌握逆向思维方式,提升思维的广度;注意总结提炼每种方法的精华之处,帮助学生搭建桥梁,建立全面的知识系统,同时进行必要的习题练习,促进学生构建完整的知识体系[3].